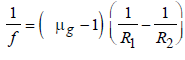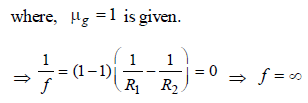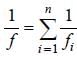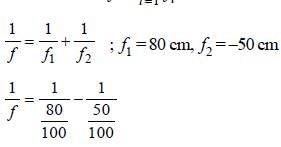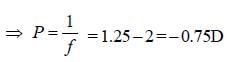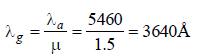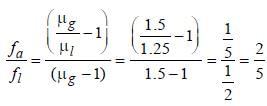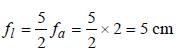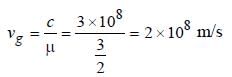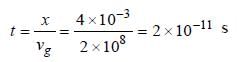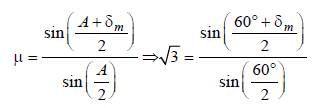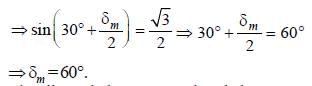All Exams >
NEET >
NEET Past Year Papers >
All Questions
All questions of Ray Optics and Optical Instruments for NEET Exam
f1’ is placed ata distance of 'd’ from a convex lens of focal length ‘f2’. A beam of light coming from infinity andfalling on this convex lens-concave mirrorcombination returns to infinity. The distance ‘d’ must equal : [2012]- a)f1 + f,
- b)–f1 + f2
- c)2f1 + f2
- d)–2f1 + f2
Correct answer is option 'C'. Can you explain this answer?
f1’ is placed ata distance of 'd’ from a convex lens of focal length ‘f2’. A beam of light coming from infinity andfalling on this convex lens-concave mirrorcombination returns to infinity. The distance ‘d’ must equal : [2012]
a)
f1 + f,
b)
–f1 + f2
c)
2f1 + f2
d)
–2f1 + f2

|
Abhishek Desai answered |
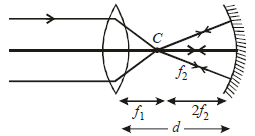
d= f1 + 2f2
Rainbow is formed due to a combination of [2000]- a)dispersion and total internal reflection
- b)refraction and absorption
- c)dispersion and focussing
- d)refraction and scattering
Correct answer is option 'A'. Can you explain this answer?
Rainbow is formed due to a combination of [2000]
a)
dispersion and total internal reflection
b)
refraction and absorption
c)
dispersion and focussing
d)
refraction and scattering

|
Arya Nair answered |
Rainbow is formed due to combination of
total internal reflection and dispersion.
total internal reflection and dispersion.
A ray of light travelling in a transparent mediumof refractive index μ , falls on a surface separatingthe medium from air at an angle of incidence of450 . For which of the following value of μ theray can undergo total internal reflection? [2010]- a)μ = 1.33
- b)μ = 1.40
- c)μ = 1.50
- d)μ = 1.25
Correct answer is option 'C'. Can you explain this answer?
A ray of light travelling in a transparent mediumof refractive index μ , falls on a surface separatingthe medium from air at an angle of incidence of450 . For which of the following value of μ theray can undergo total internal reflection? [2010]
a)
μ = 1.33
b)
μ = 1.40
c)
μ = 1.50
d)
μ = 1.25
|
|
Gowri Sen answered |
When a ray of light travels through a transparent medium of refractive index, its speed and direction change. The amount of change in speed and direction depends on the angle of incidence and the refractive index of the medium.
The refractive index of a medium is defined as the ratio of the speed of light in vacuum to the speed of light in the medium. It is denoted by the symbol n and is given by the formula:
n = c/v
where c is the speed of light in vacuum and v is the speed of light in the medium.
When a ray of light enters a medium from vacuum, it bends towards the normal. The angle of incidence i and the angle of refraction r are related to the refractive index n of the medium by Snell's law:
n1 sin i = n2 sin r
where n1 is the refractive index of the first medium (vacuum) and n2 is the refractive index of the second medium (the medium through which the light is passing).
If the angle of incidence is greater than a certain value called the critical angle, the light is totally reflected back into the first medium. This is known as total internal reflection.
The critical angle is given by:
sin c = n2/n1
where c is the critical angle.
In summary, when a ray of light travels through a transparent medium of refractive index, it bends towards the normal and its speed changes. The amount of bending and speed change depends on the angle of incidence and the refractive index of the medium. If the angle of incidence is greater than the critical angle, total internal reflection occurs.
The refractive index of a medium is defined as the ratio of the speed of light in vacuum to the speed of light in the medium. It is denoted by the symbol n and is given by the formula:
n = c/v
where c is the speed of light in vacuum and v is the speed of light in the medium.
When a ray of light enters a medium from vacuum, it bends towards the normal. The angle of incidence i and the angle of refraction r are related to the refractive index n of the medium by Snell's law:
n1 sin i = n2 sin r
where n1 is the refractive index of the first medium (vacuum) and n2 is the refractive index of the second medium (the medium through which the light is passing).
If the angle of incidence is greater than a certain value called the critical angle, the light is totally reflected back into the first medium. This is known as total internal reflection.
The critical angle is given by:
sin c = n2/n1
where c is the critical angle.
In summary, when a ray of light travels through a transparent medium of refractive index, it bends towards the normal and its speed changes. The amount of bending and speed change depends on the angle of incidence and the refractive index of the medium. If the angle of incidence is greater than the critical angle, total internal reflection occurs.
An astronomical telescope has a length of 44 cmand tenfold magnification. The focal length ofthe objective lens is [1997]- a)4 cm
- b)40 cm
- c)44 cm
- d)440 cm
Correct answer is option 'B'. Can you explain this answer?
An astronomical telescope has a length of 44 cmand tenfold magnification. The focal length ofthe objective lens is [1997]
a)
4 cm
b)
40 cm
c)
44 cm
d)
440 cm

|
Shounak Nair answered |
Given : Length of astronomical telescope
(f0 + fe) = 44 cm and magnification
(f0 + fe) = 44 cm and magnification
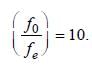
From the given magnification, we find that f0
= 10fe. Therefore, 10fe + fe = 44 or 11fe = 44 or
fe = 4. And focal length of the objective
(f0) = 44 – fe = 44 – 4 = 40 cm.
= 10fe. Therefore, 10fe + fe = 44 or 11fe = 44 or
fe = 4. And focal length of the objective
(f0) = 44 – fe = 44 – 4 = 40 cm.
Ray optics is valid, when characteristicdimensions are [1989]- a)of the same order as the wavelength of light
- b)much smaller than the wavelength of light
- c)of the order of one millimetre
- d)much larger than the wavelength of light
Correct answer is option 'D'. Can you explain this answer?
Ray optics is valid, when characteristicdimensions are [1989]
a)
of the same order as the wavelength of light
b)
much smaller than the wavelength of light
c)
of the order of one millimetre
d)
much larger than the wavelength of light

|
Sonal Kulkarni answered |
Characteristic dimensions must be much
larger than the wavelength of light.
larger than the wavelength of light.
A rod of length 10 cm lies along the principalaxis of a concave mirror of focal length 10 cm insuch a way that its end closer to the pole is20 cm away from the mirror. The length of theimage is : [2012M]- a)10 cm
- b)15 cm
- c)2.5 cm
- d)5 cm
Correct answer is option 'D'. Can you explain this answer?
A rod of length 10 cm lies along the principalaxis of a concave mirror of focal length 10 cm insuch a way that its end closer to the pole is20 cm away from the mirror. The length of theimage is : [2012M]
a)
10 cm
b)
15 cm
c)
2.5 cm
d)
5 cm

|
Muskaan Basak answered |
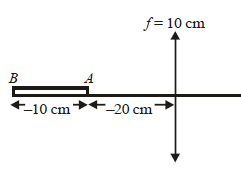
The focal length of the mirror
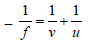
For A end of the rod the image distance
When u1 = – 20 cm
When u1 = – 20 cm
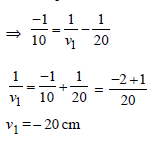
For when u2 = – 30 cm
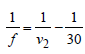
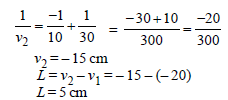
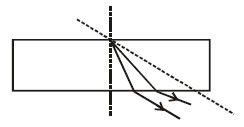
A beam of light composed of red and green raysis incident obliquely at a point on the face ofrectangular glass slab. When coming out onthe opposite parallel face, the red and green raysemerge from [2004]- a)one point propagating in the same direction
- b)two points propagating in two differentnon-parallel directions
- c)two points propagating in two differentparallel directions
- d)one point propagating in two differentdirections
Correct answer is option 'C'. Can you explain this answer?
A beam of light composed of red and green raysis incident obliquely at a point on the face ofrectangular glass slab. When coming out onthe opposite parallel face, the red and green raysemerge from [2004]
a)
one point propagating in the same direction
b)
two points propagating in two differentnon-parallel directions
c)
two points propagating in two differentparallel directions
d)
one point propagating in two differentdirections

|
Pankaj Banerjee answered |
Since refractive index for both the light are
different, so they emerge out moving in two
different parallel directions.
different, so they emerge out moving in two
different parallel directions.
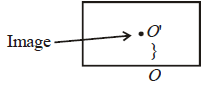
A microscope is focussed on a mark on a pieceof paper and then a slab of glass of thickness 3cm and refractive index 1.5 is placed over themark. How should the microscope be moved toget the mark in focus again ? [2006]- a)4.5 cm downward
- b)1 cm downward
- c)2 cm upward
- d)1 cm upward
Correct answer is option 'D'. Can you explain this answer?
A microscope is focussed on a mark on a pieceof paper and then a slab of glass of thickness 3cm and refractive index 1.5 is placed over themark. How should the microscope be moved toget the mark in focus again ? [2006]
a)
4.5 cm downward
b)
1 cm downward
c)
2 cm upward
d)
1 cm upward

|
Ishani Nambiar answered |
In the later case microscope will be focussed for O'. So, it is required to be lifted by distance OO'.
OO' = real depth of O – apparent depth of O.
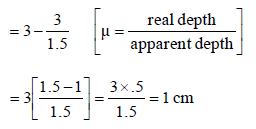
The hypermetropia is a [1995]- a)short-sight defect
- b)long-sight defect
- c)bad vision due to old age
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
The hypermetropia is a [1995]
a)
short-sight defect
b)
long-sight defect
c)
bad vision due to old age
d)
none of these

|
Mahesh Saini answered |
A person suffering from hyper metropia can
see objects beyond a particular point called
the near point. If the object lies at a point
nearer than this point, then image is not
formed at the retina. This is also known as
long-sight defect.
see objects beyond a particular point called
the near point. If the object lies at a point
nearer than this point, then image is not
formed at the retina. This is also known as
long-sight defect.
For a normal eye, the cornea of eye provides aconverging power of 40D and the leastconverging power of the eye lens behind thecornea is 20D. Using this information, thedistance between the retina and the eye lens ofthe eye can be estimated to be [NEET 2013]- a)2.5 cm
- b)1.67 cm
- c)1.5 cm
- d)5 cm
Correct answer is option 'A'. Can you explain this answer?
For a normal eye, the cornea of eye provides aconverging power of 40D and the leastconverging power of the eye lens behind thecornea is 20D. Using this information, thedistance between the retina and the eye lens ofthe eye can be estimated to be [NEET 2013]
a)
2.5 cm
b)
1.67 cm
c)
1.5 cm
d)
5 cm

|
Lakshmi Bharia answered |
Here, P1 = 40D
P2 = 20D
f eq =?
P eq = P1+ P2
= 40+20
=60D
f eq = 100/ P eq =. 100/60 = 1.67 cm.
P2 = 20D
f eq =?
P eq = P1+ P2
= 40+20
=60D
f eq = 100/ P eq =. 100/60 = 1.67 cm.
A boy is trying to start a fire by focusing sunlighton a piece of paper using an equiconvex lens offocal length 10 cm. The diameter of the Sun is 1.39 ×109 m and its mean distance from the earthis 1.5 × 1011 m. What is the diameter of the Sun’simage on the paper? [2008]- a)9.2 × 10–4 m
- b)6.5 × 10–4 m
- c)6.5 × 10–5 m
- d)12.4 × 10–4 m
Correct answer is option 'A'. Can you explain this answer?
A boy is trying to start a fire by focusing sunlighton a piece of paper using an equiconvex lens offocal length 10 cm. The diameter of the Sun is 1.39 ×109 m and its mean distance from the earthis 1.5 × 1011 m. What is the diameter of the Sun’simage on the paper? [2008]
a)
9.2 × 10–4 m
b)
6.5 × 10–4 m
c)
6.5 × 10–5 m
d)
12.4 × 10–4 m
|
|
Abhijeet Sharma answered |
× 10^6 km and its distance from Earth is approximately 150 million km. Assuming the lens has a diameter of 5 cm, what is the minimum distance the paper should be placed from the lens to start a fire?
First, we need to convert the diameter of the Sun from kilometers to centimeters:
1.39 × 10^6 km = 1.39 × 10^9 cm
Next, we need to find the angle that the Sun subtends at the lens, using the formula:
θ = 2 tan^-1 (d/2f)
where d is the diameter of the Sun and f is the focal length of the lens. Substituting the values, we get:
θ = 2 tan^-1 (1.39 × 10^9 cm / 2 × 10 cm) = 78.5°
This means that the Sun will appear to cover an angle of 78.5 degrees when viewed through the lens.
Now, we need to find the distance from the lens where the image of the Sun will be formed. Using the thin lens formula:
1/f = 1/di + 1/do
where di is the image distance and do is the object distance. We can assume that the object distance is very large compared to the focal length of the lens, so we can approximate do as infinity. This gives:
1/f = 1/di
Solving for di, we get:
di = f = 10 cm
This means that the image of the Sun will be formed at a distance of 10 cm from the lens.
Finally, we need to find the distance between the lens and the paper. This will depend on the diameter of the lens and the size of the image of the Sun. Since the diameter of the lens is 5 cm, we can assume that the image of the Sun will be smaller than this. Let's assume that the image of the Sun has a diameter of 1 cm. Then, using similar triangles, we can find the distance between the lens and the paper:
(1 cm / 1.39 × 10^9 cm) = (x / 10 cm)
Solving for x, we get:
x = 1.39 × 10^-7 cm
This is a very small distance, but it makes sense since the lens is magnifying the image of the Sun by a large factor. Therefore, the minimum distance the paper should be placed from the lens to start a fire is approximately 1.39 × 10^-7 cm. However, it is important to note that this experiment should only be attempted with extreme caution and proper safety measures in place, as focusing sunlight can be very dangerous and can cause fires or eye damage.
First, we need to convert the diameter of the Sun from kilometers to centimeters:
1.39 × 10^6 km = 1.39 × 10^9 cm
Next, we need to find the angle that the Sun subtends at the lens, using the formula:
θ = 2 tan^-1 (d/2f)
where d is the diameter of the Sun and f is the focal length of the lens. Substituting the values, we get:
θ = 2 tan^-1 (1.39 × 10^9 cm / 2 × 10 cm) = 78.5°
This means that the Sun will appear to cover an angle of 78.5 degrees when viewed through the lens.
Now, we need to find the distance from the lens where the image of the Sun will be formed. Using the thin lens formula:
1/f = 1/di + 1/do
where di is the image distance and do is the object distance. We can assume that the object distance is very large compared to the focal length of the lens, so we can approximate do as infinity. This gives:
1/f = 1/di
Solving for di, we get:
di = f = 10 cm
This means that the image of the Sun will be formed at a distance of 10 cm from the lens.
Finally, we need to find the distance between the lens and the paper. This will depend on the diameter of the lens and the size of the image of the Sun. Since the diameter of the lens is 5 cm, we can assume that the image of the Sun will be smaller than this. Let's assume that the image of the Sun has a diameter of 1 cm. Then, using similar triangles, we can find the distance between the lens and the paper:
(1 cm / 1.39 × 10^9 cm) = (x / 10 cm)
Solving for x, we get:
x = 1.39 × 10^-7 cm
This is a very small distance, but it makes sense since the lens is magnifying the image of the Sun by a large factor. Therefore, the minimum distance the paper should be placed from the lens to start a fire is approximately 1.39 × 10^-7 cm. However, it is important to note that this experiment should only be attempted with extreme caution and proper safety measures in place, as focusing sunlight can be very dangerous and can cause fires or eye damage.
There is a prism with refractive index equal to √2 and the refracting angle equal to 30°. One of the refracting surfaces of the prism is polished. A beam of monochromatic light will retrace its path if its angle of incidence over the refracting surface of the prism is [1992]- a)0°
- b)30°
- c)45°
- d)60°
Correct answer is option 'C'. Can you explain this answer?
There is a prism with refractive index equal to √2 and the refracting angle equal to 30°. One of the refracting surfaces of the prism is polished. A beam of monochromatic light will retrace its path if its angle of incidence over the refracting surface of the prism is [1992]
a)
0°
b)
30°
c)
45°
d)
60°

|
Shanaya Rane answered |
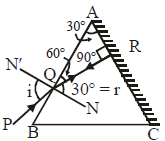
It is clear from the figure that the ray will
retrace the path when the refracted ray QR is
incident normally on the polished surface AC.
Thus, angle of refraction r = 30°
retrace the path when the refracted ray QR is
incident normally on the polished surface AC.
Thus, angle of refraction r = 30°
A convex lens and a concave lens, each havingsame focal length of 25 cm, are put in contact toform a combination of lenses. The power indiopters of the combination is [2006]- a)50
- b)infinite
- c)zero
- d)25
Correct answer is option 'C'. Can you explain this answer?
A convex lens and a concave lens, each havingsame focal length of 25 cm, are put in contact toform a combination of lenses. The power indiopters of the combination is [2006]
a)
50
b)
infinite
c)
zero
d)
25

|
Devansh Mehra answered |
From the formula,
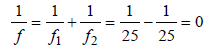
Power of combination 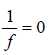
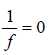
A point source of light is placed 4 m below thesurface of water of refractive index 5/3. Theminimum diameter of a disc, which should beplaced over the source, on the surface of waterto cut off all light coming out of water is [1994]- a)∞
- b)6 m
- c)4 m
- d)3 m
Correct answer is option 'B'. Can you explain this answer?
A point source of light is placed 4 m below thesurface of water of refractive index 5/3. Theminimum diameter of a disc, which should beplaced over the source, on the surface of waterto cut off all light coming out of water is [1994]
a)
∞
b)
6 m
c)
4 m
d)
3 m

|
Pallabi Reddy answered |
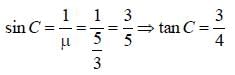
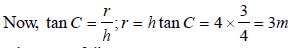
A person is six feet tall. How tall must a verticalmirror be if he is able to see his entire length?- a)3 ft
- b)4.5 ft [2000]
- c)7.5 ft
- d)6 ft
Correct answer is option 'A'. Can you explain this answer?
A person is six feet tall. How tall must a verticalmirror be if he is able to see his entire length?
a)
3 ft
b)
4.5 ft [2000]
c)
7.5 ft
d)
6 ft
|
|
Anu Sharma answered |
Explanation:
To see his entire length in the mirror, the person needs to see from the top of his head to the bottom of his feet. Since the person is six feet tall, the mirror needs to be tall enough to reflect his full height.
The mirror needs to be at least six feet tall to reflect the entire length of the person.
Since option D states that the mirror should be six feet tall, it is the correct answer.
Why the other options are incorrect:
a) 3 ft: This option is incorrect because a mirror that is only three feet tall would not be able to reflect the person's full height. The person would only be able to see half of his body in the mirror.
b) 4.5 ft: This option is incorrect because a mirror that is 4.5 feet tall would still not be able to reflect the person's full height. The person would only be able to see three-quarters of his body in the mirror.
c) 7.5 ft: This option is incorrect because a mirror that is 7.5 feet tall would be too tall and would extend beyond the person's height. The person would not be able to see his full height in the mirror.
In summary:
The correct answer is option D, which states that the mirror should be six feet tall. This height would allow the person to see his entire length in the mirror.
To see his entire length in the mirror, the person needs to see from the top of his head to the bottom of his feet. Since the person is six feet tall, the mirror needs to be tall enough to reflect his full height.
The mirror needs to be at least six feet tall to reflect the entire length of the person.
Since option D states that the mirror should be six feet tall, it is the correct answer.
Why the other options are incorrect:
a) 3 ft: This option is incorrect because a mirror that is only three feet tall would not be able to reflect the person's full height. The person would only be able to see half of his body in the mirror.
b) 4.5 ft: This option is incorrect because a mirror that is 4.5 feet tall would still not be able to reflect the person's full height. The person would only be able to see three-quarters of his body in the mirror.
c) 7.5 ft: This option is incorrect because a mirror that is 7.5 feet tall would be too tall and would extend beyond the person's height. The person would not be able to see his full height in the mirror.
In summary:
The correct answer is option D, which states that the mirror should be six feet tall. This height would allow the person to see his entire length in the mirror.
A telescope has an objective lens of 10 cmdiameter and is situated at a distance of onekilometer from two objects. The minimumdistance between these two objects, which canbe resolved by the telescope, when the meanwavelength of light is 5000 Å, is of the order of [2004]- a)5 cm
- b)0.5 m
- c)5 m
- d)5 mm
Correct answer is option 'D'. Can you explain this answer?
A telescope has an objective lens of 10 cmdiameter and is situated at a distance of onekilometer from two objects. The minimumdistance between these two objects, which canbe resolved by the telescope, when the meanwavelength of light is 5000 Å, is of the order of [2004]
a)
5 cm
b)
0.5 m
c)
5 m
d)
5 mm

|
Sneha Basak answered |
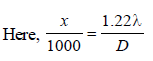
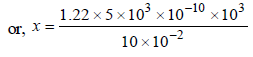
or, x = 1.22 × 5 × 10–3 m = 6.1 mm
∴ x is of the order of 5 mm.
∴ x is of the order of 5 mm.
An air bubble in a glass slab (μ = 1.5) is 5 cmdeep when viewed from one face and 2 cm deepwhen viewed from the opposite face. Thethickness of the slab is [2000]- a)7.5 cm
- b)10.5 cm
- c)7 cm
- d)10 cm
Correct answer is option 'B'. Can you explain this answer?
An air bubble in a glass slab (μ = 1.5) is 5 cmdeep when viewed from one face and 2 cm deepwhen viewed from the opposite face. Thethickness of the slab is [2000]
a)
7.5 cm
b)
10.5 cm
c)
7 cm
d)
10 cm

|
Manoj Sengupta answered |
Also known as a lens) will behave differently depending on its position within the slab.
If the air bubble is in the middle of the slab, it will act as a diverging lens. This means that it will cause light rays passing through it to spread out, or diverge. This can be observed by looking through the slab and seeing objects appear smaller and farther away than they actually are.
On the other hand, if the air bubble is closer to one of the surfaces of the slab, it will act as a converging lens. This means that it will cause light rays passing through it to come together, or converge. This can be observed by looking through the slab and seeing objects appear larger and closer than they actually are.
The behavior of the air bubble as a lens is due to the difference in refractive index between the air inside the bubble and the glass slab. The refractive index is a measure of how much light is bent or refracted when it passes through a material. In the case of the air bubble, the difference in refractive index between the air and the glass causes the light rays passing through the bubble to bend, resulting in the lens-like behavior.
It is worth noting that the effect of the air bubble as a lens may be more pronounced if the slab is made of a material with a higher refractive index, such as glass or plastic. Additionally, the size and shape of the air bubble can also affect its lens-like behavior.
If the air bubble is in the middle of the slab, it will act as a diverging lens. This means that it will cause light rays passing through it to spread out, or diverge. This can be observed by looking through the slab and seeing objects appear smaller and farther away than they actually are.
On the other hand, if the air bubble is closer to one of the surfaces of the slab, it will act as a converging lens. This means that it will cause light rays passing through it to come together, or converge. This can be observed by looking through the slab and seeing objects appear larger and closer than they actually are.
The behavior of the air bubble as a lens is due to the difference in refractive index between the air inside the bubble and the glass slab. The refractive index is a measure of how much light is bent or refracted when it passes through a material. In the case of the air bubble, the difference in refractive index between the air and the glass causes the light rays passing through the bubble to bend, resulting in the lens-like behavior.
It is worth noting that the effect of the air bubble as a lens may be more pronounced if the slab is made of a material with a higher refractive index, such as glass or plastic. Additionally, the size and shape of the air bubble can also affect its lens-like behavior.
A body is located on a wall. Its image of equal size is to be obtained on a parallel wall with the help of a convex lens. The lens is placed at a distance 'd' ahead of second wall, then the required focal length will be [2002]- a)only d/4
- b)only d/2
- c)more than d/4 but less than d/2
- d)less than d/4
Correct answer is option 'B'. Can you explain this answer?
A body is located on a wall. Its image of equal size is to be obtained on a parallel wall with the help of a convex lens. The lens is placed at a distance 'd' ahead of second wall, then the required focal length will be [2002]
a)
only d/4
b)
only d/2
c)
more than d/4 but less than d/2
d)
less than d/4

|
Kajal Bose answered |
Using the lens formula
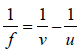
Given v = d, for equal size image |v | =|u| d
By sign convention u = –d
By sign convention u = –d
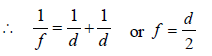
One face of a rectangular glass plate 6 cm thick issilvered. An object held 8 cm in front of the firstface forms an image 12 cm behind the silveredface. The refractive index of the glass is [1996]- a)0.4
- b)0.8
- c)1.2
- d)1.6
Correct answer is option 'C'. Can you explain this answer?
One face of a rectangular glass plate 6 cm thick issilvered. An object held 8 cm in front of the firstface forms an image 12 cm behind the silveredface. The refractive index of the glass is [1996]
a)
0.4
b)
0.8
c)
1.2
d)
1.6

|
Pallabi Reddy answered |
Thickness of glass plate (t) = 6 cm;
Distance of the object (u) = 8 cm.
And distance of the image (v) = 12 cm.
Let x = Apparent position of the silvered
surface in cm.
Since the image is formed due to relfection at
the silvered face and by the property of mirror
image
Distance of object from the mirror = Distance
of image from the mirror
or, x + 8 = 12 + 6 – x ⇒ x = 5 cm.
Therefore, refractive index of glass
Distance of the object (u) = 8 cm.
And distance of the image (v) = 12 cm.
Let x = Apparent position of the silvered
surface in cm.
Since the image is formed due to relfection at
the silvered face and by the property of mirror
image
Distance of object from the mirror = Distance
of image from the mirror
or, x + 8 = 12 + 6 – x ⇒ x = 5 cm.
Therefore, refractive index of glass
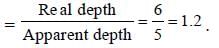
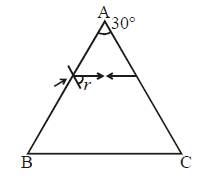
The refractive index of the material of a prism is√2 and its refracting angle is 30º. One of therefracting surfaces of the prism is made a mirrorinwards. A beam of monochromatic light entersthe prism from the mirrored surface, then its angleof incidence of the prism is [2004]- a)30º
- b)45º
- c)60º
- d)0º
Correct answer is option 'B'. Can you explain this answer?
The refractive index of the material of a prism is√2 and its refracting angle is 30º. One of therefracting surfaces of the prism is made a mirrorinwards. A beam of monochromatic light entersthe prism from the mirrored surface, then its angleof incidence of the prism is [2004]
a)
30º
b)
45º
c)
60º
d)
0º
|
|
Harsh Desai answered |
∠r = 30° (using law of triangle)
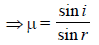
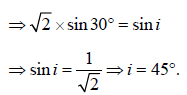
A luminous object is placed at a distance of 30 cm from the convex lens of focal length 20 cm. On theother side of the lens, at what distance from thelens a convex mirror of radius of curvature 10 cmbe placed in order to have an upright image of theobject coincident with it? [1998]- a)12 cm
- b)30 cm
- c)50 cm
- d)60 cm
Correct answer is option 'C'. Can you explain this answer?
A luminous object is placed at a distance of 30 cm from the convex lens of focal length 20 cm. On theother side of the lens, at what distance from thelens a convex mirror of radius of curvature 10 cmbe placed in order to have an upright image of theobject coincident with it? [1998]
a)
12 cm
b)
30 cm
c)
50 cm
d)
60 cm

|
Akshat Chavan answered |
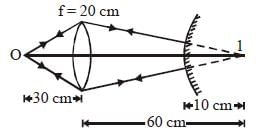
For the lens,
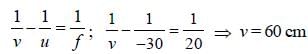
Coincidence is possible when the image is
formed at the centre of curvature of the
mirror. Only then the rays refracting through
the lens will fall normally on the convex mirror
and retrace their path to form the image at O.
So, the distance between lens and mirror
= 60 – 10 = 50 cm.
formed at the centre of curvature of the
mirror. Only then the rays refracting through
the lens will fall normally on the convex mirror
and retrace their path to form the image at O.
So, the distance between lens and mirror
= 60 – 10 = 50 cm.
Two plane mirrors are inclined at 70°. A rayincident on one mirror at angle θ after reflectionfalls on second mirror and is reflected from thereparallel to first mirror. The value of θ is[NEET Kar. 2013]- a)50°
- b)45°
- c)30°
- d)55°
Correct answer is option 'A'. Can you explain this answer?
Two plane mirrors are inclined at 70°. A rayincident on one mirror at angle θ after reflectionfalls on second mirror and is reflected from thereparallel to first mirror. The value of θ is[NEET Kar. 2013]
a)
50°
b)
45°
c)
30°
d)
55°

|
Maheshwar Saini answered |
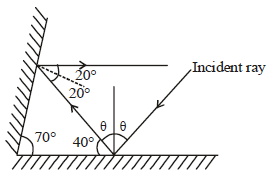
From fig. 40° + θ = 90° ∴ θ = 90° – 40° = 50°
The radius of curvature of a thin plano-convexlens is 10 cm (of curved surface) and the refractiveindex is 1.5. If the plane surface is silvered, thenit behaves like a concave mirror of focal length [2000]- a)10 cm
- b)15 cm
- c)20 cm
- d)5 cm
Correct answer is option 'A'. Can you explain this answer?
The radius of curvature of a thin plano-convexlens is 10 cm (of curved surface) and the refractiveindex is 1.5. If the plane surface is silvered, thenit behaves like a concave mirror of focal length [2000]
a)
10 cm
b)
15 cm
c)
20 cm
d)
5 cm

|
Rahul Kumar answered |

A biconvex lens has a radius of curvature ofmagnitude 20 cm. Which one of the followingoptions best describe the image formed of anobject of height 2 cm placed 30 cm from the lens? [2011]
- a)Virtual, upright, height = 1 cm
- b)Virtual, upright, height = 0.5 cm
- c)Real, inverted, height = - 4 cm
- d)Real, inverted, height = 1cm
Correct answer is option 'C'. Can you explain this answer?
A biconvex lens has a radius of curvature ofmagnitude 20 cm. Which one of the followingoptions best describe the image formed of anobject of height 2 cm placed 30 cm from the lens? [2011]
a)
Virtual, upright, height = 1 cm
b)
Virtual, upright, height = 0.5 cm
c)
Real, inverted, height = - 4 cm
d)
Real, inverted, height = 1cm
|
|
Gauri Datta answered |
Explanation:
- The given lens is a biconvex lens with radius of curvature as 20 cm.
- Since the object is placed at a distance of 30 cm from the lens, it is outside the focal length.
- Using lens formula, we have:
- 1/f = 1/v - 1/u
- Here, u = -30 cm (negative sign represents that object is placed to the left of the lens)
- f = R/2 = 20/2 = 10 cm
- On substituting the values, we get:
- 1/10 = 1/v + 1/30
- On solving, we get v = 15 cm
- Since the image is formed at a distance of 15 cm from the lens, it is behind the lens and real.
- The height of the object is given as 2 cm.
- Using magnification formula, we have:
- m = -v/u
- On substituting the values, we get:
- m = -15/-30 = 0.5
- The magnification is positive, which means that the image is upright.
- Since the magnification is less than 1, the image is smaller than the object.
- The height of the image can be calculated using the formula:
- h' = mh
- On substituting the values, we get:
- h' = 0.5 x 2 = 1 cm
- Therefore, the image formed is real, inverted and has a height of 1 cm.
- Option (C) is the correct answer.
An achromatic combination of lenses is formedby joining [1995]- a)2 convex lenses
- b)2 concave lenses
- c)1 convex and 1 concave lens
- d)1 convex and 1 plane mirror
Correct answer is option 'C'. Can you explain this answer?
An achromatic combination of lenses is formedby joining [1995]
a)
2 convex lenses
b)
2 concave lenses
c)
1 convex and 1 concave lens
d)
1 convex and 1 plane mirror

|
Akshat Chavan answered |
If two or more lenses are combined together
in such a way that this combination
produces images of different colours at the
same point and of the same size, then this
property is called ‘achromatism’. Concave
and convex type of lenses are used for this
combination.
in such a way that this combination
produces images of different colours at the
same point and of the same size, then this
property is called ‘achromatism’. Concave
and convex type of lenses are used for this
combination.
When a biconvex lens of glass having refractiveindex 1.47 is dipped in a liquid, it acts as a planesheet of glass. This implies that the liquid musthave refractive index. [2012]- a)equal to that of glass
- b)less then one
- c)greater than that of glass
- d)less then that of glass
Correct answer is option 'A'. Can you explain this answer?
When a biconvex lens of glass having refractiveindex 1.47 is dipped in a liquid, it acts as a planesheet of glass. This implies that the liquid musthave refractive index. [2012]
a)
equal to that of glass
b)
less then one
c)
greater than that of glass
d)
less then that of glass

|
Gowri Nair answered |
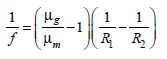
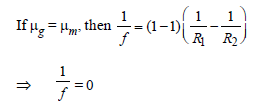
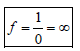
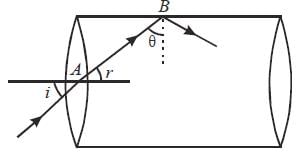
Light enters at an angle of incidence in atransparent rod of refractive index n. For whatvalue of the refractive index of the material ofthe rod the light once entered into it will notleave it through its lateral face whatsoever bethe value of angle of incidence? [1998]- a)n > √2
- b)n = 1
- c)n = 1.1
- d)n = 1.3
Correct answer is option 'A'. Can you explain this answer?
Light enters at an angle of incidence in atransparent rod of refractive index n. For whatvalue of the refractive index of the material ofthe rod the light once entered into it will notleave it through its lateral face whatsoever bethe value of angle of incidence? [1998]
a)
n > √2
b)
n = 1
c)
n = 1.1
d)
n = 1.3

|
Prashanth Dasgupta answered |
Let a ray of light enter at A and the refracted
beam is AB. This is incident at an angle θ.
For no refraction at the lateral face, θ > C
or, sin θ > sin C But θ+ r =90°⇒θ= (90° – r)
beam is AB. This is incident at an angle θ.
For no refraction at the lateral face, θ > C
or, sin θ > sin C But θ+ r =90°⇒θ= (90° – r)

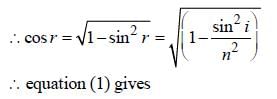

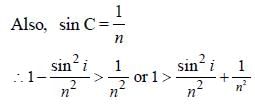
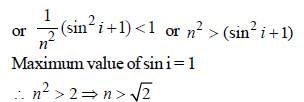
If fV and fR are the focal lengths of a convex lensfor violet and red light respectively and FV and FR are the focal lengths of concave lens for violetand red light respectively, then we have [1996]- a)fV < fR and FV > FR
- b)fV < fR and FV < FR
- c)fV > fR and FV > FR
- d)fV > fR and FV < FR
Correct answer is option 'A'. Can you explain this answer?
If fV and fR are the focal lengths of a convex lensfor violet and red light respectively and FV and FR are the focal lengths of concave lens for violetand red light respectively, then we have [1996]
a)
fV < fR and FV > FR
b)
fV < fR and FV < FR
c)
fV > fR and FV > FR
d)
fV > fR and FV < FR

|
Palak Khanna answered |
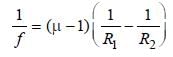
According to Cauchy relation
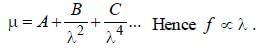
Hence, red light having maximum wavelength
has maximum focal length.
has maximum focal length.
∴ fv < fr and also Fv > Fr as focal length is
negative for a concave lens.
negative for a concave lens.
The reddish appearance of the sun at sunriseand sunset is due to [NEET Kar. 2013]- a)the colour of the sky
- b)the scattering of light
- c)the polarisation of light
- d)the colour of the sun
Correct answer is option 'B'. Can you explain this answer?
The reddish appearance of the sun at sunriseand sunset is due to [NEET Kar. 2013]
a)
the colour of the sky
b)
the scattering of light
c)
the polarisation of light
d)
the colour of the sun

|
Nayanika Dasgupta answered |
It is due to scattering of light. Scattering 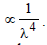 Hence the light reaches us is rich in
Hence the light reaches us is rich in
red
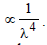 Hence the light reaches us is rich in
Hence the light reaches us is rich inred
The frequency of a light wave in a material is2 × 1014 Hz and wavelength is 5000 Å. Therefractive index of material will be [2007]- a)1.50
- b)3.00
- c)1.33
- d)1.40
Correct answer is option 'B'. Can you explain this answer?
The frequency of a light wave in a material is2 × 1014 Hz and wavelength is 5000 Å. Therefractive index of material will be [2007]
a)
1.50
b)
3.00
c)
1.33
d)
1.40

|
Tejas Chavan answered |
By using v = nλ
Here, n = 2 x1014Hz
Here, n = 2 x1014Hz
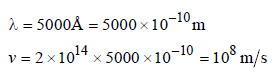
Refractive index of the material,
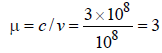
An equiconvex lens is cut into two halves along (i) XOX' and (ii) YOY' as shown in the figure. Let f, f ', f '' be the focal lengths of the complete lens, of each half in case (i), and of each half in case (ii), respectively. [2003]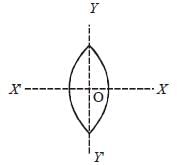 Choose the correct statement from the following
Choose the correct statement from the following- a)f ' = 2f, f '' = 2f
- b)f ' = f, f '' = 2f
- c)f ' = 2f, f '' = f
- d)f ' = f, f '' = f
Correct answer is option 'B'. Can you explain this answer?
An equiconvex lens is cut into two halves along (i) XOX' and (ii) YOY' as shown in the figure. Let f, f ', f '' be the focal lengths of the complete lens, of each half in case (i), and of each half in case (ii), respectively. [2003]

Choose the correct statement from the following
a)
f ' = 2f, f '' = 2f
b)
f ' = f, f '' = 2f
c)
f ' = 2f, f '' = f
d)
f ' = f, f '' = f

|
Maheshwar Saini answered |
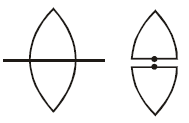
In this case, R1 and R2 are unchanged
So, f will remain unchanged for both pieces
of the lens
∴ f = f '
So, f will remain unchanged for both pieces
of the lens
∴ f = f '
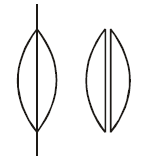
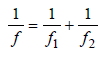
This is combination of two lenses of equal
focal lengths
focal lengths
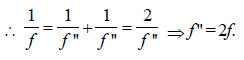
A small coin is resting on the bottom of a beaker filled with liquid. A ray of light from the coin travels upto the surface of the liquid and moves along its surface. How fast is the light travelling in the liquid? [2007]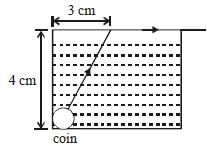
- a)2.4 × 108 m/s
- b)3.0 × 108 m/s
- c)1.2 × 108 m/s
- d)1.8 × 108 m/s
Correct answer is option 'D'. Can you explain this answer?
A small coin is resting on the bottom of a beaker filled with liquid. A ray of light from the coin travels upto the surface of the liquid and moves along its surface. How fast is the light travelling in the liquid? [2007]

a)
2.4 × 108 m/s
b)
3.0 × 108 m/s
c)
1.2 × 108 m/s
d)
1.8 × 108 m/s

|
Rhea Sarkar answered |
Hypotenuse comes out to be 5 cm.
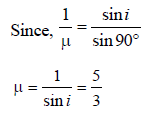
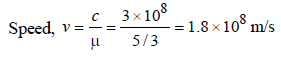
Two thin lenses of focal lengths f1 and f2 are in contact and coaxial. The power of the combination is: [2008]- a)
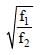
- b)
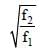
- c)
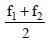
- d)
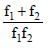
Correct answer is option 'D'. Can you explain this answer?
Two thin lenses of focal lengths f1 and f2 are in contact and coaxial. The power of the combination is: [2008]
a)
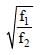
b)
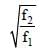
c)
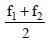
d)
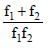

|
Ishaan Menon answered |
The focal length of the combination
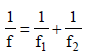
∴ Power of the combinations
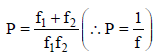
A ray is incident at an angle of incidence i on one surface of a prism of small angle A and emerges normally from the opposite surface. If the refractive index of the material of prism is μ, the angle of incidence i is nearly equal to [1989]- a)
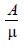
- b)
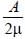
- c)μA
- d)μA/2
Correct answer is option 'C'. Can you explain this answer?
A ray is incident at an angle of incidence i on one surface of a prism of small angle A and emerges normally from the opposite surface. If the refractive index of the material of prism is μ, the angle of incidence i is nearly equal to [1989]
a)
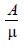
b)
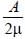
c)
μA
d)
μA/2

|
Mahesh Saini answered |
As refracted ray emerges normally from
oppostite surface, r2 = 0
oppostite surface, r2 = 0
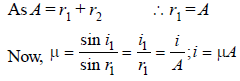
A beam of monochromatic light is refracted fromvacuum into a medium of refractive index 1.5,the wavelength of refracted light will be (1991]- a)dependent on intensity of refracted light
- b)same
- c)smaller
- d)larger
Correct answer is option 'C'. Can you explain this answer?
A beam of monochromatic light is refracted fromvacuum into a medium of refractive index 1.5,the wavelength of refracted light will be (1991]
a)
dependent on intensity of refracted light
b)
same
c)
smaller
d)
larger

|
Mahesh Saini answered |
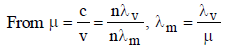
Here, c = velocity of light in medium and v =
velocity of light in vacuum;
m = refractive index of the medium.
Hence, wavelength in medium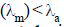
velocity of light in vacuum;
m = refractive index of the medium.
Hence, wavelength in medium
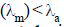
(∴ μ > 1, given)
So, the required wavelength decreases.
ALTERNATIVELY,
c =vλ . On refraction, the frequency, v do
not change. When light is refracted from
vacuum to a medium, the velocity, c
decreases. Therefore, λ also decreases
ALTERNATIVELY,
c =vλ . On refraction, the frequency, v do
not change. When light is refracted from
vacuum to a medium, the velocity, c
decreases. Therefore, λ also decreases
A light ray falls on a rectangular glass slab as shown. The index of refraction of the glass, if total internal reflection is to occur at the vertical face, is [2002]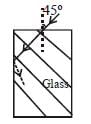
- a)
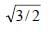
- b)
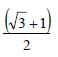
- c)
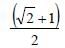
- d)
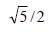
Correct answer is option 'A'. Can you explain this answer?
A light ray falls on a rectangular glass slab as shown. The index of refraction of the glass, if total internal reflection is to occur at the vertical face, is [2002]

a)
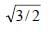
b)
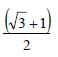
c)
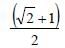
d)
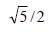

|
Charvi Shah answered |
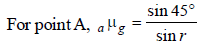

For point B, sin (90° – r) = gμa where,
(90° – r) is critical angle.
(90° – r) is critical angle.
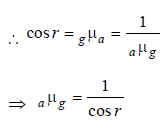
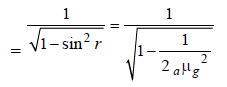

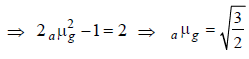
Light travels through a glass plate of thickness t and refractive index μ. If c is the speed of light in vacuum, the time taken by light to travel this thickness of glass is- a)μtc
- b)tc/μ
- c)t/μc
- d)μt/c
Correct answer is option 'D'. Can you explain this answer?
Light travels through a glass plate of thickness t and refractive index μ. If c is the speed of light in vacuum, the time taken by light to travel this thickness of glass is
a)
μtc
b)
tc/μ
c)
t/μc
d)
μt/c

|
Muskaan Basak answered |
Total thickness = t; Refrative index = μ
Speed of light in Glass plate = c/μ
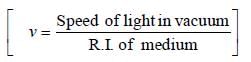
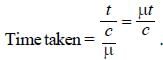
[where, t = thickness of glass plate]
Which of the following is not due to total internalreflection? [2011]- a)Working of optical fibre
- b)Difference between apparent and real depthof pond
- c)Mirage on hot summer days
- d)Brilliance of diamond
Correct answer is option 'B'. Can you explain this answer?
Which of the following is not due to total internalreflection? [2011]
a)
Working of optical fibre
b)
Difference between apparent and real depthof pond
c)
Mirage on hot summer days
d)
Brilliance of diamond

|
Nayanika Dasgupta answered |
Difference between apparent and real depth
of a pond is due to the refraction of light,
not due to the total internal reflection. Other
three phenomena are due to the total
internal reflection.
of a pond is due to the refraction of light,
not due to the total internal reflection. Other
three phenomena are due to the total
internal reflection.
A thin prism of angle 15º made of glass ofrefractive index μ1 = 1.5 is combined with anotherprism of glass of refractive index μ2 = 1.75. Thecombination of the prism produces dispersionwithout deviation. The angle of the second prismshould be [2011M]- a)7°
- b)10°
- c)12°
- d)5°
Correct answer is option 'B'. Can you explain this answer?
A thin prism of angle 15º made of glass ofrefractive index μ1 = 1.5 is combined with anotherprism of glass of refractive index μ2 = 1.75. Thecombination of the prism produces dispersionwithout deviation. The angle of the second prismshould be [2011M]
a)
7°
b)
10°
c)
12°
d)
5°

|
Tejas Chavan answered |
Deviation = zero
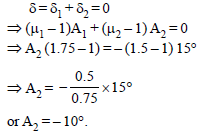
or A2 = – 10°.
Negative sign shows that the second prism
is inverted with respect to the first.
Negative sign shows that the second prism
is inverted with respect to the first.
A converging beam of rays is incident on adiverging lens. Having passed through the lensthe rays intersect at a point 15 cm from the lenson the opposite side. If the lens is removedthe point where the rays meet will move 5 cmcloser to the lens. The focal length of the lensis [2011M]- a)– 10 cm
- b)20 cm
- c)–30 cm
- d)5 cm
Correct answer is option 'C'. Can you explain this answer?
A converging beam of rays is incident on adiverging lens. Having passed through the lensthe rays intersect at a point 15 cm from the lenson the opposite side. If the lens is removedthe point where the rays meet will move 5 cmcloser to the lens. The focal length of the lensis [2011M]
a)
– 10 cm
b)
20 cm
c)
–30 cm
d)
5 cm

|
Subhankar Datta answered |
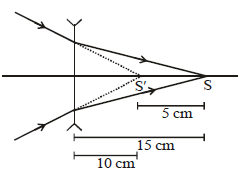
By lens formula
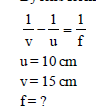
Putting the values, we get
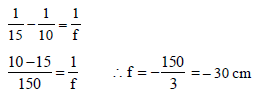
An electromagnetic radiation of frequency n, wavelength λ, travelling with velocity v in air enters in a glass slab of refractive index (ν). The frequency, wavelength and velocity of light in the glass slab will be respectively [1997]- a)
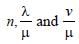
- b)
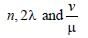
- c)
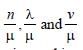
- d)
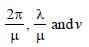
Correct answer is option 'A'. Can you explain this answer?
An electromagnetic radiation of frequency n, wavelength λ, travelling with velocity v in air enters in a glass slab of refractive index (ν). The frequency, wavelength and velocity of light in the glass slab will be respectively [1997]
a)
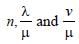
b)
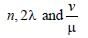
c)
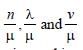
d)
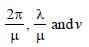

|
Maya Sengupta answered |
When electromagnetic wave enters in other
medium, frequency reamains unchanged
while wavelength and velocity become 1/μ times.
medium, frequency reamains unchanged
while wavelength and velocity become 1/μ times.
So, For e.m. wave entering from air to glass
slab (μ), frequency remains n,
slab (μ), frequency remains n,
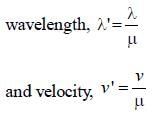
Chapter doubts & questions for Ray Optics and Optical Instruments - NEET Past Year Papers 2025 is part of NEET exam preparation. The chapters have been prepared according to the NEET exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for NEET 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Ray Optics and Optical Instruments - NEET Past Year Papers in English & Hindi are available as part of NEET exam.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup