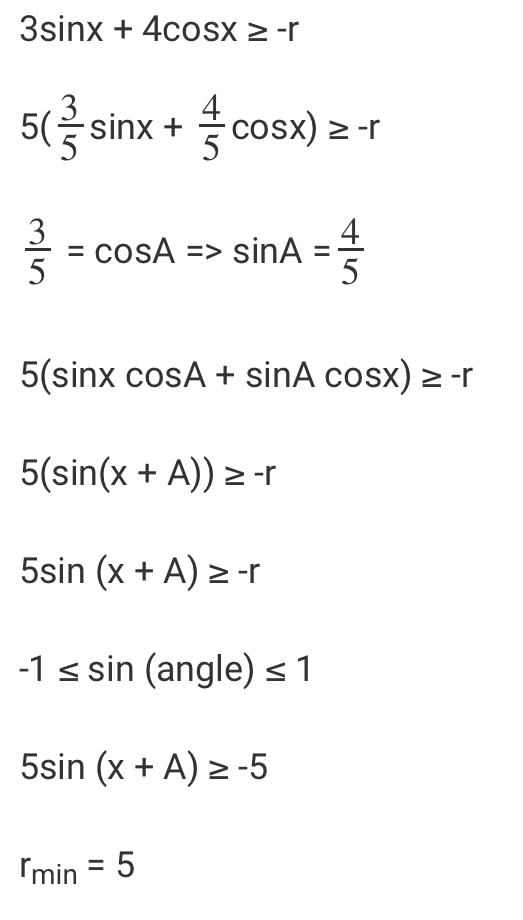All Exams >
ACT >
Mathematics for ACT >
All Questions
All questions of Trigonometry for ACT Exam
A right angled triangle has a height ‘p’, base ‘b’ and hypotenuse ‘h’. Which of the following value can h2 not take, given that p and b are positive integers?- a)74
- b)52
- c)13
- d)23
Correct answer is option 'D'. Can you explain this answer?
A right angled triangle has a height ‘p’, base ‘b’ and hypotenuse ‘h’. Which of the following value can h2 not take, given that p and b are positive integers?
a)
74
b)
52
c)
13
d)
23

|
Imk Pathshala answered |
We know that,
h2 = p2 + b2 Given, p and b are positive integer, so h2 will be sum of two perfect squares. We see
a) 72 + 52 = 74
b) 62 + 42 = 52
c) 32 + 22 = 13
d) Can’t be expressed as a sum of two perfect squares
The question is "Which of the following value can h2 not take, given that p and b are positive integers? "
Hence, the answer is 23
h2 = p2 + b2 Given, p and b are positive integer, so h2 will be sum of two perfect squares. We see
a) 72 + 52 = 74
b) 62 + 42 = 52
c) 32 + 22 = 13
d) Can’t be expressed as a sum of two perfect squares
The question is "Which of the following value can h2 not take, given that p and b are positive integers? "
Hence, the answer is 23
What will be the value of 2cos2 θ - 1, if cos4 θ - sin4 θ = 2/3?- a)1
- b)2
- c)3/2
- d)2/3
Correct answer is option 'D'. Can you explain this answer?
What will be the value of 2cos2 θ - 1, if cos4 θ - sin4 θ = 2/3?
a)
1
b)
2
c)
3/2
d)
2/3
|
|
Joshua Pope answered |
It appears that the expression "2cos2" is incomplete and does not make mathematical sense. In order to provide an answer, please provide the full expression or specify what you are referring to.
Which of the following is the correct value of cos2 550 + cos2 350 + sin2 650 + sin2 250?- a)0
- b)3
- c)2
- d)None of the above
Correct answer is option 'C'. Can you explain this answer?
Which of the following is the correct value of cos2 550 + cos2 350 + sin2 650 + sin2 250?
a)
0
b)
3
c)
2
d)
None of the above
|
|
Liam Curry answered |
To determine the value of cos2550, cos2350, sin2650, and sin2250, we need to use the unit circle and the properties of trigonometric functions.
1. Cosine of 2550:
To find the cosine of 2550, we need to locate the angle 2550 degrees on the unit circle. Since the unit circle is divided into 360 degrees, we can subtract 360 from 2550 to get an equivalent angle within one full rotation:
2550 - 360 = 2190 degrees
Now, locate 2190 degrees on the unit circle. The cosine value is the x-coordinate of the point on the unit circle corresponding to the angle. From the unit circle, we can see that the x-coordinate at 2190 degrees is 1. Therefore, cos2550 = 1.
2. Cosine of 2350:
Similarly, we need to find the equivalent angle within one full rotation for 2350 degrees:
2350 - 360 = 1990 degrees
Locate 1990 degrees on the unit circle. The x-coordinate at 1990 degrees is -1. Therefore, cos2350 = -1.
3. Sine of 2650:
To find the sine of 2650, we need to locate the angle 2650 degrees on the unit circle. Again, find the equivalent angle within one full rotation:
2650 - 360 = 2290 degrees
Locate 2290 degrees on the unit circle. The y-coordinate at 2290 degrees is 1. Therefore, sin2650 = 1.
4. Sine of 2250:
Similarly, find the equivalent angle within one full rotation for 2250 degrees:
2250 - 360 = 1890 degrees
Locate 1890 degrees on the unit circle. The y-coordinate at 1890 degrees is -1. Therefore, sin2250 = -1.
Hence, the correct values are:
cos2550 = 1
cos2350 = -1
sin2650 = 1
sin2250 = -1
None of the given options (a, b, d) matches these values, so the correct answer is option 'C' (2).
1. Cosine of 2550:
To find the cosine of 2550, we need to locate the angle 2550 degrees on the unit circle. Since the unit circle is divided into 360 degrees, we can subtract 360 from 2550 to get an equivalent angle within one full rotation:
2550 - 360 = 2190 degrees
Now, locate 2190 degrees on the unit circle. The cosine value is the x-coordinate of the point on the unit circle corresponding to the angle. From the unit circle, we can see that the x-coordinate at 2190 degrees is 1. Therefore, cos2550 = 1.
2. Cosine of 2350:
Similarly, we need to find the equivalent angle within one full rotation for 2350 degrees:
2350 - 360 = 1990 degrees
Locate 1990 degrees on the unit circle. The x-coordinate at 1990 degrees is -1. Therefore, cos2350 = -1.
3. Sine of 2650:
To find the sine of 2650, we need to locate the angle 2650 degrees on the unit circle. Again, find the equivalent angle within one full rotation:
2650 - 360 = 2290 degrees
Locate 2290 degrees on the unit circle. The y-coordinate at 2290 degrees is 1. Therefore, sin2650 = 1.
4. Sine of 2250:
Similarly, find the equivalent angle within one full rotation for 2250 degrees:
2250 - 360 = 1890 degrees
Locate 1890 degrees on the unit circle. The y-coordinate at 1890 degrees is -1. Therefore, sin2250 = -1.
Hence, the correct values are:
cos2550 = 1
cos2350 = -1
sin2650 = 1
sin2250 = -1
None of the given options (a, b, d) matches these values, so the correct answer is option 'C' (2).
If tan θ + cot θ = 2, then what is the value of tan100 θ + cot100 θ?- a)1
- b)3
- c)2
- d)None of the above
Correct answer is option 'C'. Can you explain this answer?
If tan θ + cot θ = 2, then what is the value of tan100 θ + cot100 θ?
a)
1
b)
3
c)
2
d)
None of the above
|
|
Ayesha Joshi answered |
Given tan θ + cot θ = 2
Put θ = 450, above equation will satisfy as,
1 + 1 = 2
So, θ = 450,
= tan100 450 + cot100 450
= 1100 + 1100
= 2
Put θ = 450, above equation will satisfy as,
1 + 1 = 2
So, θ = 450,
= tan100 450 + cot100 450
= 1100 + 1100
= 2
If the value of sin A + cosec A = 2, then what is the value of sin7 A + cosec7 A?- a)1
- b)0
- c)2
- d)3
Correct answer is option 'C'. Can you explain this answer?
If the value of sin A + cosec A = 2, then what is the value of sin7 A + cosec7 A?
a)
1
b)
0
c)
2
d)
3
|
|
Ayesha Joshi answered |
It is given that sin A + cosec A = 2 ……(i)
On putting A = 900, then above condition will satisfy
sin 900 + cosec 900 = 2
or, 1 + 1 = 2 (as the equation satisfies, so, A = 900)
Now, sin7 A + cosec7 A = ?
⇒ sin7 900 + cosec7 900
⇒ 17 + 17
= 2
On putting A = 900, then above condition will satisfy
sin 900 + cosec 900 = 2
or, 1 + 1 = 2 (as the equation satisfies, so, A = 900)
Now, sin7 A + cosec7 A = ?
⇒ sin7 900 + cosec7 900
⇒ 17 + 17
= 2
Which of the following is the correct value of (3 / 1+tan2 θ) + 2 sin2 θ + (1 / 1+cot2 θ)?- a)3
- b)9
- c)6
- d)None of the above
Correct answer is option 'A'. Can you explain this answer?
Which of the following is the correct value of (3 / 1+tan2 θ) + 2 sin2 θ + (1 / 1+cot2 θ)?
a)
3
b)
9
c)
6
d)
None of the above
|
|
Ayesha Joshi answered |
(3 / 1+tan2 θ) + 2 sin2 θ + (1 / 1+cot2 θ) = ?
According to the trigonometric identities, the given equation can be written as -
= 3/sec2 θ + 2 sin2 θ + 1/cosec2 θ
= 3cos2 θ + 2 sin2 θ + sin2 θ
= 3cos2 θ + 3sin2 θ
= 3(cos2 θ + sin2 θ)
= 3
According to the trigonometric identities, the given equation can be written as -
= 3/sec2 θ + 2 sin2 θ + 1/cosec2 θ
= 3cos2 θ + 2 sin2 θ + sin2 θ
= 3cos2 θ + 3sin2 θ
= 3(cos2 θ + sin2 θ)
= 3
What will be the value of sec4 θ - tan4 θ, if sec2 θ + tan2 θ = 7/12?- a)1/2
- b)7/12
- c)1
- d)2/3
Correct answer is option 'B'. Can you explain this answer?
What will be the value of sec4 θ - tan4 θ, if sec2 θ + tan2 θ = 7/12?
a)
1/2
b)
7/12
c)
1
d)
2/3
|
|
Ayesha Joshi answered |
Given sec2 θ + tan2 θ = 7/12
Now, here we can apply the formula -
a4 - b4 = (a2 - b2) (a2 + b2)
sec4 θ - tan4 θ = (sec2 θ - tan2 θ) (sec2 θ + tan2 θ)
= 1 x (sec2 θ + tan2 θ) {because 1 + tan2 θ = sec2 θ}
= 1 x 7/12
= 7/12
Now, here we can apply the formula -
a4 - b4 = (a2 - b2) (a2 + b2)
sec4 θ - tan4 θ = (sec2 θ - tan2 θ) (sec2 θ + tan2 θ)
= 1 x (sec2 θ + tan2 θ) {because 1 + tan2 θ = sec2 θ}
= 1 x 7/12
= 7/12
What will be the numerical value of (4 sec2 300 + cos2 600 - tan2 450) / (sin2 300 + cos2 300)?- a)55/12
- b)45/12
- c)1/12
- d)None of the above
Correct answer is option 'A'. Can you explain this answer?
What will be the numerical value of (4 sec2 300 + cos2 600 - tan2 450) / (sin2 300 + cos2 300)?
a)
55/12
b)
45/12
c)
1/12
d)
None of the above
|
|
Ayesha Joshi answered |
Given: (4 sec2 300 + cos2 600 - tan2 450) / (sin2 300 + cos2 300)
We have to put the numerical values,
= [4 (2/√3)2 + (½)2 - (1)2] / 1
⇒ sec2 A - 1 = 1 + 2 (sec2 B - 1)
⇒ sec2 A - 1 = 1 + 2 sec2 B - 2
⇒ sec2 A - 1 = 2 sec2 B - 1
⇒ 1/cos2 A = 2/cos2 B
⇒ cos2 B = 2cos2 A
⇒ or, cos B = √2 cos A
⇒ So, √2 cos A - cos B = 0
We have to put the numerical values,
= [4 (2/√3)2 + (½)2 - (1)2] / 1
⇒ sec2 A - 1 = 1 + 2 (sec2 B - 1)
⇒ sec2 A - 1 = 1 + 2 sec2 B - 2
⇒ sec2 A - 1 = 2 sec2 B - 1
⇒ 1/cos2 A = 2/cos2 B
⇒ cos2 B = 2cos2 A
⇒ or, cos B = √2 cos A
⇒ So, √2 cos A - cos B = 0
A man standing on top of a tower sees a car coming towards the tower. If it takes 20 minutes for the angle of depression to change from 30° to 60°, what is the time remaining for the car to reach the tower?- a)20√3 minutes
- b)10 minutes
- c)10√3 minutes
- d)5 minutes
Correct answer is option 'B'. Can you explain this answer?
A man standing on top of a tower sees a car coming towards the tower. If it takes 20 minutes for the angle of depression to change from 30° to 60°, what is the time remaining for the car to reach the tower?
a)
20√3 minutes
b)
10 minutes
c)
10√3 minutes
d)
5 minutes

|
Quantronics answered |
What is the value of tan3θ, If tan7θ.tan2θ = 1?- a)√3
- b)1/√3
- c)-1/√3
- d)None of the above
Correct answer is option 'B'. Can you explain this answer?
What is the value of tan3θ, If tan7θ.tan2θ = 1?
a)
√3
b)
1/√3
c)
-1/√3
d)
None of the above

|
Orion Classes answered |
Given tan7θ.tan2θ = 1
As we know, if tanA . tanB = 1 then, A + B = 900
So, 7θ + 3θ = 900
⇒ 9θ = 900
Or, θ = 100
Now, we have to find tan3θ
So, put θ = 100 in tan3θ, we will get
tan 300 = 1/√3
As we know, if tanA . tanB = 1 then, A + B = 900
So, 7θ + 3θ = 900
⇒ 9θ = 900
Or, θ = 100
Now, we have to find tan3θ
So, put θ = 100 in tan3θ, we will get
tan 300 = 1/√3
If sin (θ + 180) = cos 600, then what is the value of cos5θ, where 00 < θ < 900?- a)0
- b)1/2
- c)1
- d)2
Correct answer is option 'B'. Can you explain this answer?
If sin (θ + 180) = cos 600, then what is the value of cos5θ, where 00 < θ < 900?
a)
0
b)
1/2
c)
1
d)
2

|
Orion Classes answered |
Given sin (θ + 180) = cos 600
sin (θ + 180) = cos (900 - 300)
So, sin (θ + 180) = sin300
Then, θ = 300 - 180
θ = 120
So, cos5θ = cos 5 x 120
= cos 600
= 1/2
sin (θ + 180) = cos (900 - 300)
So, sin (θ + 180) = sin300
Then, θ = 300 - 180
θ = 120
So, cos5θ = cos 5 x 120
= cos 600
= 1/2
If tan θ - cot θ = 0, what will be the value of sin θ + cos θ?- a)1
- b)√2
- c)1/√2
- d)None of the above
Correct answer is option 'B'. Can you explain this answer?
If tan θ - cot θ = 0, what will be the value of sin θ + cos θ?
a)
1
b)
√2
c)
1/√2
d)
None of the above
|
|
Lucy Jenkins answered |
Understanding the Equation
When tan θ - cot θ = 0, it implies that:
- tan θ = cot θ
We know that:
- tan θ = sin θ / cos θ
- cot θ = cos θ / sin θ
Setting these equal gives:
- sin θ / cos θ = cos θ / sin θ
Cross Multiplying
Cross multiplying leads to:
- sin² θ = cos² θ
This can be rewritten using the Pythagorean identity:
- sin² θ + cos² θ = 1
Finding the Values of sin θ and cos θ
From sin² θ = cos² θ, we can infer:
- sin² θ = 1/2
- cos² θ = 1/2
Thus, we have:
- sin θ = ± 1/√2
- cos θ = ± 1/√2
Calculating sin θ + cos θ
Now, we need to find:
- sin θ + cos θ = ± 1/√2 ± 1/√2
Considering both positive values, we get:
- sin θ + cos θ = 1/√2 + 1/√2 = 2/√2 = √2
Conclusion
Hence, the value of sin θ + cos θ is:
- √2
Thus, the correct answer is option 'B'.
When tan θ - cot θ = 0, it implies that:
- tan θ = cot θ
We know that:
- tan θ = sin θ / cos θ
- cot θ = cos θ / sin θ
Setting these equal gives:
- sin θ / cos θ = cos θ / sin θ
Cross Multiplying
Cross multiplying leads to:
- sin² θ = cos² θ
This can be rewritten using the Pythagorean identity:
- sin² θ + cos² θ = 1
Finding the Values of sin θ and cos θ
From sin² θ = cos² θ, we can infer:
- sin² θ = 1/2
- cos² θ = 1/2
Thus, we have:
- sin θ = ± 1/√2
- cos θ = ± 1/√2
Calculating sin θ + cos θ
Now, we need to find:
- sin θ + cos θ = ± 1/√2 ± 1/√2
Considering both positive values, we get:
- sin θ + cos θ = 1/√2 + 1/√2 = 2/√2 = √2
Conclusion
Hence, the value of sin θ + cos θ is:
- √2
Thus, the correct answer is option 'B'.
Suppose cos θ + sin θ = √2 cos θ, then which of the following is the correct value of cos θ - sin θ?- a)√2 cos θ
- b)√2 sin θ
- c)-√2 cos θ
- d)-√2 sin θ
Correct answer is option 'B'. Can you explain this answer?
Suppose cos θ + sin θ = √2 cos θ, then which of the following is the correct value of cos θ - sin θ?
a)
√2 cos θ
b)
√2 sin θ
c)
-√2 cos θ
d)
-√2 sin θ
|
|
Ayesha Joshi answered |
It is given that, cos θ + sin θ = √2 cos θ …..(i)
On squaring both sides, we will get,
(cos θ + sin θ)2 = (√2 cos θ)2
⇒ cos2 θ + sin2 θ + 2 sin θ cos θ = 2 cos2 θ
Or, 2cos2 θ - cos2 θ - sin2 θ = 2 sinθ cosθ
⇒ cos2 θ - sin2 θ = 2 sin θ cos θ
⇒ (cos θ + sin θ) (cos θ - sin θ) = 2 sin θ cos θ
⇒ (√2 cos θ) (cos θ - sin θ) = 2 sin θ cos θ [from equation (i)]
⇒ (cos θ - sin θ) = 2 sinθ cosθ / √2 cos θ
= √2 sin θ
On squaring both sides, we will get,
(cos θ + sin θ)2 = (√2 cos θ)2
⇒ cos2 θ + sin2 θ + 2 sin θ cos θ = 2 cos2 θ
Or, 2cos2 θ - cos2 θ - sin2 θ = 2 sinθ cosθ
⇒ cos2 θ - sin2 θ = 2 sin θ cos θ
⇒ (cos θ + sin θ) (cos θ - sin θ) = 2 sin θ cos θ
⇒ (√2 cos θ) (cos θ - sin θ) = 2 sin θ cos θ [from equation (i)]
⇒ (cos θ - sin θ) = 2 sinθ cosθ / √2 cos θ
= √2 sin θ
Which of the following is the correct value of (5/sec2 θ) + 3 sin2 θ + (2 / 1+cot2 θ)?- a)3
- b)9
- c)5
- d)None of the above
Correct answer is option 'C'. Can you explain this answer?
Which of the following is the correct value of (5/sec2 θ) + 3 sin2 θ + (2 / 1+cot2 θ)?
a)
3
b)
9
c)
5
d)
None of the above
|
|
Ayesha Joshi answered |
(5 / sec2 θ) + 3 sin2 θ + (2 / 1+cot2 θ) = ?
According to the trigonometric identities, the given equation can be written as -
= 5cos2 θ + 3 sin2 θ + 2/cosec2 θ
= 5cos2 θ + 3 sin2 θ + 2sin2 θ
= 5cos2 θ + 5sin2 θ
= 5(cos2 θ + sin2 θ)
= 5
According to the trigonometric identities, the given equation can be written as -
= 5cos2 θ + 3 sin2 θ + 2/cosec2 θ
= 5cos2 θ + 3 sin2 θ + 2sin2 θ
= 5cos2 θ + 5sin2 θ
= 5(cos2 θ + sin2 θ)
= 5
If the value of sin(θ + 300) is 3/√12, then what is the value of cos2 θ?- a)3/4
- b)4/3
- c)1/4
- d)None of the above
Correct answer is option 'A'. Can you explain this answer?
If the value of sin(θ + 300) is 3/√12, then what is the value of cos2 θ?
a)
3/4
b)
4/3
c)
1/4
d)
None of the above
|
|
Ayesha Joshi answered |
Given sin (θ + 300) = 3/√12
It can be written as sin (θ + 300) = 3/2√3
Or, sin (θ + 300) = √3/2
⇒ sin (θ + 300) = sin 600
⇒ θ + 300 = 600
⇒ θ = 300
On putting θ = 300, in cos2 θ, we will get
cos2 300 = (√3/2)2
= 3/4
It can be written as sin (θ + 300) = 3/2√3
Or, sin (θ + 300) = √3/2
⇒ sin (θ + 300) = sin 600
⇒ θ + 300 = 600
⇒ θ = 300
On putting θ = 300, in cos2 θ, we will get
cos2 300 = (√3/2)2
= 3/4
What is the value of (tan2 θ - sec2 θ)?- a)2
- b)-1
- c)1
- d)None of the above
Correct answer is option 'B'. Can you explain this answer?
What is the value of (tan2 θ - sec2 θ)?
a)
2
b)
-1
c)
1
d)
None of the above

|
Orion Classes answered |
(tan2 θ - sec2 θ)
= sin2 θ/cos2 θ - 1/cos2 θ
= (sin2 θ - 1) / cos2 θ
= - cos2 θ/cos2 θ
= -1
= sin2 θ/cos2 θ - 1/cos2 θ
= (sin2 θ - 1) / cos2 θ
= - cos2 θ/cos2 θ
= -1
If the value of tan2 θ + tan4 θ = 1, what will be the value of cos2 θ + cos4 θ?- a)4
- b)1
- c)-2
- d)-1
Correct answer is option 'B'. Can you explain this answer?
If the value of tan2 θ + tan4 θ = 1, what will be the value of cos2 θ + cos4 θ?
a)
4
b)
1
c)
-2
d)
-1
|
|
Ayesha Joshi answered |
Given, tan2 θ + tan4 θ = 1 …. (i)
From equation (i),
tan2 θ ( 1 + tan2 θ ) = 1
tan2 θ ( sec2 θ ) = 1 [As according to the trigonometric identity, sec2 θ - tan2 θ = 1]
tan2 θ = 1/ sec2 θ
tan2 θ = cos2 θ ….(ii)
Now, cos2 θ + cos4 θ = ?
⇒ cos2 θ + (cos2)2 θ
⇒ tan2 θ + (tan2)2 θ
⇒ tan2 θ + tan4 θ
= 1 {from equation (i)}
From equation (i),
tan2 θ ( 1 + tan2 θ ) = 1
tan2 θ ( sec2 θ ) = 1 [As according to the trigonometric identity, sec2 θ - tan2 θ = 1]
tan2 θ = 1/ sec2 θ
tan2 θ = cos2 θ ….(ii)
Now, cos2 θ + cos4 θ = ?
⇒ cos2 θ + (cos2)2 θ
⇒ tan2 θ + (tan2)2 θ
⇒ tan2 θ + tan4 θ
= 1 {from equation (i)}
If the value of θ + φ = π/2, and sin θ = 1/2, what will be the value of sinφ?- a)1
- b)√2
- c)√3/2
- d)2/√3
Correct answer is option 'C'. Can you explain this answer?
If the value of θ + φ = π/2, and sin θ = 1/2, what will be the value of sinφ?
a)
1
b)
√2
c)
√3/2
d)
2/√3
|
|
Hannah Cooper answered |
An item decreases by 20%, the new value of the item is 80% of its original value.
Which of the following is the correct value of cot 100.cot 200.cot 600.cot 700.cot 800?- a)1/√3
- b)√3
- c)-1
- d)1
Correct answer is option 'A'. Can you explain this answer?
Which of the following is the correct value of cot 100.cot 200.cot 600.cot 700.cot 800?
a)
1/√3
b)
√3
c)
-1
d)
1

|
Orion Classes answered |
Here, we can apply the formula -
cot A. cot B = 1 (when A + B = 900)
= (cot 200 . cot 700) x (cot 100 . cot 800) x cot 600
= 1 x 1 x 1/√3
= 1/√3
So, the correct value of cot 100.cot 200.cot 600.cot 700.cot 800 = 1/√3
cot A. cot B = 1 (when A + B = 900)
= (cot 200 . cot 700) x (cot 100 . cot 800) x cot 600
= 1 x 1 x 1/√3
= 1/√3
So, the correct value of cot 100.cot 200.cot 600.cot 700.cot 800 = 1/√3
Which of the following is the correct relation between A and B, if A = tan 110 . tan 290, and B = 2 cot 610 . cot 790?- a)A = B
- b)A = -B
- c)A = 2B
- d)2A = B
Correct answer is option 'D'. Can you explain this answer?
Which of the following is the correct relation between A and B, if A = tan 110 . tan 290, and B = 2 cot 610 . cot 790?
a)
A = B
b)
A = -B
c)
A = 2B
d)
2A = B
|
|
Ayesha Joshi answered |
Given A = tan 110 . tan 290, and B = 2 cot 610 . cot 790
A / B = tan 110 . tan 290 / 2 cot 610 . cot 790
= [tan 110 . tan 290] / [2 cot (900 - 290) . cot (900 - 110)]
= tan 110 . tan 290 / 2 tan 110 . tan 290
= 1/2
So, A/B = 1/2
Or, 2A = B
A / B = tan 110 . tan 290 / 2 cot 610 . cot 790
= [tan 110 . tan 290] / [2 cot (900 - 290) . cot (900 - 110)]
= tan 110 . tan 290 / 2 tan 110 . tan 290
= 1/2
So, A/B = 1/2
Or, 2A = B
Find the value of :- (log sin 1° + log sin 2° ………..+ log sin 89°) + (log tan 1° + log tan 2° + ……… + log tan 89°) - (log cos 1° + log cos 2° + ……… + log cos 89°)- a)log √2/(1+√2)
- b)-1
- c)1
- d)none of these
Correct answer is option 'D'. Can you explain this answer?
Find the value of :- (log sin 1° + log sin 2° ………..+ log sin 89°) + (log tan 1° + log tan 2° + ……… + log tan 89°) - (log cos 1° + log cos 2° + ……… + log cos 89°)
a)
log √2/(1+√2)
b)
-1
c)
1
d)
none of these
|
|
Vikas Choudhury answered |
Writing the equation as :-
(log sin 1degree - log cos 89degree) + (log sin 2degree - log cos 88degree) + (log sin 3degree - log cos 87degree)… + log tan 1degree. log tan 89degree + log tan 2degree. log tan 88degree + ….
=) As cos(90−ϕ)=sinϕ:tan(90−ϕ)=cotϕ
=) (log sin 1degree - log sin 1degree) +(log sin 2degree - log sin 2degree)+…..+ log tan 1degree cot 1degree + log tan 2degree cot 2degree
=) log 1 = 0
If the value of tan θ = 4/3, then which of the following is the correct value of (3 sin θ + 2 cos θ) / (3 sin θ - 2 cos θ) = ?- a)1
- b)-3
- c)2
- d)3
Correct answer is option 'D'. Can you explain this answer?
If the value of tan θ = 4/3, then which of the following is the correct value of (3 sin θ + 2 cos θ) / (3 sin θ - 2 cos θ) = ?
a)
1
b)
-3
c)
2
d)
3
|
|
Ayesha Joshi answered |
It is given that, tan θ = 4/3
⇒ sin θ / cos θ = 4/3
So sin θ = 4, and cos θ = 3
Now, on putting the values of sin θ and cos θ in (3 sin θ + 2 cos θ) / (3 sin θ - 2 cos θ), we will get -
= 3x4 + 2x3/ 3x4 - 2x3
= 18/6
= 3
⇒ sin θ / cos θ = 4/3
So sin θ = 4, and cos θ = 3
Now, on putting the values of sin θ and cos θ in (3 sin θ + 2 cos θ) / (3 sin θ - 2 cos θ), we will get -
= 3x4 + 2x3/ 3x4 - 2x3
= 18/6
= 3
A student is standing with a banner at the top of a 100 m high college building. From a point on the ground, the angle of elevation of the top of the student is 60° and from the same point, the angle of elevation of the top of the tower is 45°. Find the height of the student.- a)35 m
- b)73.2 m
- c)50 m
- d)75m
Correct answer is option 'B'. Can you explain this answer?
A student is standing with a banner at the top of a 100 m high college building. From a point on the ground, the angle of elevation of the top of the student is 60° and from the same point, the angle of elevation of the top of the tower is 45°. Find the height of the student.
a)
35 m
b)
73.2 m
c)
50 m
d)
75m
|
|
Abhiram Kumar answered |
Let BC be the height of the tower and DC be the height of the student.
Two poles of equal height are standing opposite to each other on either side of a road which is 100 m wide. Find a point between them on road, angles of elevation of their tops are 30∘ and 60∘. The height of each pole in meter, is:- a) 25√3
- b)20√3
- c)28√3
- d)30√3
Correct answer is option 'A'. Can you explain this answer?
Two poles of equal height are standing opposite to each other on either side of a road which is 100 m wide. Find a point between them on road, angles of elevation of their tops are 30∘ and 60∘. The height of each pole in meter, is:
a)
25√3
b)
20√3
c)
28√3
d)
30√3
|
|
Mita Mehta answered |
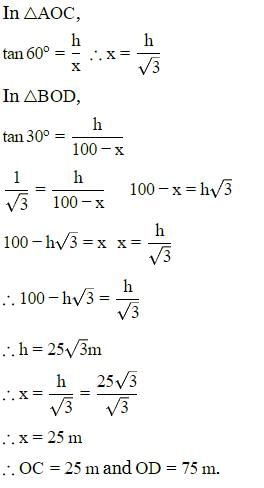
Evaluate:sin2 5° + sin2 10° + sin2 15° + …… + sin2 85° + sin2 90°- a)7
- b)8
- c)9
- d)19/2
Correct answer is option 'D'. Can you explain this answer?
Evaluate:
sin2 5° + sin2 10° + sin2 15° + …… + sin2 85° + sin2 90°
a)
7
b)
8
c)
9
d)
19/2
|
|
Ayesha Joshi answered |
Concept:
I. sin (90° - θ) = cos θ
II. sin2 θ + cos2 θ = 1
I. sin (90° - θ) = cos θ
II. sin2 θ + cos2 θ = 1
Calculation:
⇒ sin2 5° + sin2 10° + sin2 15° + …… + sin2 85° + sin2 90°
= (sin2 5° + sin2 85°) + (sin2 10° + sin2 80°) + ….. +(sin2 40° + sin2 50°)+ sin2 45° + sin2 90°
= (sin2 5° + sin2 (90° - 5°)) + (sin2 10° + sin2 (90° - 10°)) + ….. +(sin2 40° + sin2 (90° - 40°))+ sin2 45° + sin2 90°
As we know that, sin (90° - θ) = cos θ
= (sin2 5° + cos2 5°) + (sin2 10° + cos2 10°) + ….. +(sin2 40° + cos2 40°)+ sin2 45° + sin2 90°
As we know that, sin2 θ + cos2 θ = 1
= 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + (1/√2)2 + 1
= 9 + (1/2) = 19/2
⇒ sin2 5° + sin2 10° + sin2 15° + …… + sin2 85° + sin2 90°
= (sin2 5° + sin2 85°) + (sin2 10° + sin2 80°) + ….. +(sin2 40° + sin2 50°)+ sin2 45° + sin2 90°
= (sin2 5° + sin2 (90° - 5°)) + (sin2 10° + sin2 (90° - 10°)) + ….. +(sin2 40° + sin2 (90° - 40°))+ sin2 45° + sin2 90°
As we know that, sin (90° - θ) = cos θ
= (sin2 5° + cos2 5°) + (sin2 10° + cos2 10°) + ….. +(sin2 40° + cos2 40°)+ sin2 45° + sin2 90°
As we know that, sin2 θ + cos2 θ = 1
= 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + (1/√2)2 + 1
= 9 + (1/2) = 19/2
What will be the value of 1 - 2sin2 θ, if cos4 θ - sin4 θ = 2/3?- a)1
- b)2
- c)3/2
- d)2/3
Correct answer is option 'D'. Can you explain this answer?
What will be the value of 1 - 2sin2 θ, if cos4 θ - sin4 θ = 2/3?
a)
1
b)
2
c)
3/2
d)
2/3
|
|
Ayesha Joshi answered |
Given cos4 θ - sin4 θ = 2/3
Now, here we can apply the formula -
a4 - b4 = (a2 - b2) (a2 + b2)
So, (cos2 θ - sin2 θ) (cos2 θ + sin2 θ) = 2/3
So, 1 x (cos2 θ - sin2 θ) = 2/3 (because cos2 θ + sin2 θ = 1)
⇒ (1 - sin2 θ) - sin2 θ = 2/3
So, 1 - 2sin2 θ = 2/3
Now, here we can apply the formula -
a4 - b4 = (a2 - b2) (a2 + b2)
So, (cos2 θ - sin2 θ) (cos2 θ + sin2 θ) = 2/3
So, 1 x (cos2 θ - sin2 θ) = 2/3 (because cos2 θ + sin2 θ = 1)
⇒ (1 - sin2 θ) - sin2 θ = 2/3
So, 1 - 2sin2 θ = 2/3
If 2sinθ/cos3θ = tan 270° - tan θ, find the value of θ?- a)45°
- b)135°
- c)100°
- d)90°
Correct answer is option 'D'. Can you explain this answer?
If 2sinθ/cos3θ = tan 270° - tan θ, find the value of θ?
a)
45°
b)
135°
c)
100°
d)
90°

|
Orion Classes answered |
Formula:
sin2θ = 2sinθcosθ
sin(A - B) = sinAcosB - cosAsinB
sin2θ = 2sinθcosθ
sin(A - B) = sinAcosB - cosAsinB
Calculation:
Multiplying the left hand side with cosθ, we get-
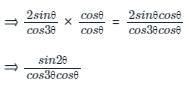
Multiplying the left hand side with cosθ, we get-
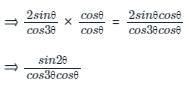
sin2θ can also be written as sin(3θ - θ)
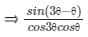
Applying sin(A-B) formula in the numerator part, we get-
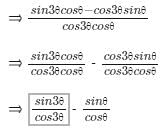
⇒ tan3θ - tanθ
Equating LHS with RHS, we get-
⇒ tan3θ - tanθ = tan 270° - tan θ
⇒ 3θ = 270°
⇒ θ = 90°
∴ The value of θ is 90°
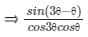
Applying sin(A-B) formula in the numerator part, we get-
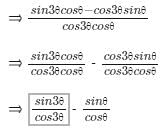
⇒ tan3θ - tanθ
Equating LHS with RHS, we get-
⇒ tan3θ - tanθ = tan 270° - tan θ
⇒ 3θ = 270°
⇒ θ = 90°
∴ The value of θ is 90°
Practice Quiz or MCQ (Multiple Choice Questions) with solutions are available for Practice, which would help you prepare for "Trigonometry" under Quantitative Aptitude. You can practice these practice quizzes as per your speed and improvise the topic. The same topic is covered under various competitive examinations like - CAT, GMAT, Bank PO, SSC and other competitive examinations. Q. 3sinx + 4cosx + r is always greater than or equal to 0. What is the smallest value ‘r’ can to take?- a)5
- b)-5
- c)4
- d)3
Correct answer is option 'A'. Can you explain this answer?
Practice Quiz or MCQ (Multiple Choice Questions) with solutions are available for Practice, which would help you prepare for "Trigonometry" under Quantitative Aptitude. You can practice these practice quizzes as per your speed and improvise the topic. The same topic is covered under various competitive examinations like - CAT, GMAT, Bank PO, SSC and other competitive examinations.
Q. 3sinx + 4cosx + r is always greater than or equal to 0. What is the smallest value ‘r’ can to take?
a)
5
b)
-5
c)
4
d)
3

|
Dhruv Mehra answered |
3sinx + 4cosx ≥ -r
5(3/5sinx+4/5cosx) ≥ -r
35 = cosA => sinA =45
5(sinx cosA + sinA cosA) ≥ -r
5(sin(x + A)) ≥ -r
5sin (x + A) ≥ -r
-1 ≤ sin (angle) ≤ 1
5sin (x + A) ≥ -5
rmin = 5
Ram and Shyam are 10 km apart. They both see a hot air balloon passing in the sky making an angle of 60° and 30° respectively. What is the height at which the balloon could be flying?- a)
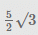
- b)5√3
- c)Both A and B
- d)Can’t be determined
Correct answer is option 'C'. Can you explain this answer?
Ram and Shyam are 10 km apart. They both see a hot air balloon passing in the sky making an angle of 60° and 30° respectively. What is the height at which the balloon could be flying?
a)
b)
5√3
c)
Both A and B
d)
Can’t be determined
|
|
Vikas Choudhury answered |
What is  equal to?
equal to?- a)sin θ - cos θ
- b)sin θ + cos θ
- c)2sin θ
- d)2cos θ
Correct answer is option 'B'. Can you explain this answer?
What is  equal to?
equal to?
 equal to?
equal to?a)
sin θ - cos θ
b)
sin θ + cos θ
c)
2sin θ
d)
2cos θ
|
|
Ayesha Joshi answered |
Formula Used:
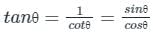
a2 - b2 = (a - b) (a + b)
Calculation:
We have to find the value of
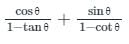
tan θ & cot θ can be written as,
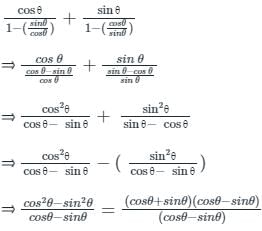
Hence,
 (sin θ + cos θ)
(sin θ + cos θ)
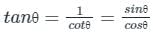
a2 - b2 = (a - b) (a + b)
Calculation:
We have to find the value of
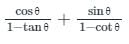
tan θ & cot θ can be written as,
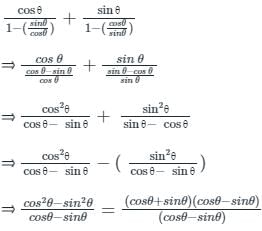
Hence,
 (sin θ + cos θ)
(sin θ + cos θ)If p = cosec θ – cot θ and q = (cosec θ + cot θ)-1 then which one of the following is correct?- a)p - q = 1
- b)p = q
- c)p + q = 1
- d)p + q = 0
Correct answer is option 'B'. Can you explain this answer?
If p = cosec θ – cot θ and q = (cosec θ + cot θ)-1 then which one of the following is correct?
a)
p - q = 1
b)
p = q
c)
p + q = 1
d)
p + q = 0
|
|
Ayesha Joshi answered |
Concept:
cosec2 x – cot2 x = 1
cosec2 x – cot2 x = 1
Calculation:
Given: p = cosec θ – cot θ and q = (cosec θ + cot θ)-1
⇒ cosec θ + cot θ = 1/q
As we know that, cosec2 x – cot2 x = 1
⇒ (cosec θ + cot θ) × (cosec θ – cot θ) = 1
1/q × p = 1
⇒ p = q
Given: p = cosec θ – cot θ and q = (cosec θ + cot θ)-1
⇒ cosec θ + cot θ = 1/q
As we know that, cosec2 x – cot2 x = 1
⇒ (cosec θ + cot θ) × (cosec θ – cot θ) = 1
1/q × p = 1
⇒ p = q
If tan 48° tan 23° tan 42° tan 67° = tan(A + 30°) then A will be- a)30∘
- b)15∘
- c)45∘
- d)60∘
Correct answer is option 'B'. Can you explain this answer?
If tan 48° tan 23° tan 42° tan 67° = tan(A + 30°) then A will be
a)
30∘
b)
15∘
c)
45∘
d)
60∘
|
|
Samantha Nguyen answered |
Understanding the Problem
To solve the equation tan 48° tan 23° tan 42° tan 67° = tan(A + 30°), we need to simplify the left-hand side and explore relationships between the angles.
Using Angle Identities
1. Complementary Angles:
- We know that tan(90° - x) = cot(x).
- Therefore, tan 67° = cot 23° and tan 42° = cot 48°.
2. Rewriting the Expression:
- This gives us:
- tan 48° tan 23° tan 42° tan 67° = tan 48° cot 48° tan 23° cot 23°.
- Both tan 48° and cot 48° multiply to 1, and the same for tan 23° and cot 23°:
- Thus, tan 48° cot 48° = 1 and tan 23° cot 23° = 1.
3. Final Simplification:
- Therefore, tan 48° tan 23° tan 42° tan 67° = 1.
Equating Both Sides
Now we have 1 = tan(A + 30°).
Finding A
1. Using the tan Identity:
- The tangent of an angle is 1 when the angle is 45° (plus any integer multiple of 180°).
- Therefore, A + 30° = 45°.
2. Solving for A:
- Thus, A = 45° - 30° = 15°.
Conclusion
The value of A is 15°, confirming that the correct answer is option 'B'. This demonstrates how understanding complementary angles and the properties of tangent can simplify the problem effectively.
To solve the equation tan 48° tan 23° tan 42° tan 67° = tan(A + 30°), we need to simplify the left-hand side and explore relationships between the angles.
Using Angle Identities
1. Complementary Angles:
- We know that tan(90° - x) = cot(x).
- Therefore, tan 67° = cot 23° and tan 42° = cot 48°.
2. Rewriting the Expression:
- This gives us:
- tan 48° tan 23° tan 42° tan 67° = tan 48° cot 48° tan 23° cot 23°.
- Both tan 48° and cot 48° multiply to 1, and the same for tan 23° and cot 23°:
- Thus, tan 48° cot 48° = 1 and tan 23° cot 23° = 1.
3. Final Simplification:
- Therefore, tan 48° tan 23° tan 42° tan 67° = 1.
Equating Both Sides
Now we have 1 = tan(A + 30°).
Finding A
1. Using the tan Identity:
- The tangent of an angle is 1 when the angle is 45° (plus any integer multiple of 180°).
- Therefore, A + 30° = 45°.
2. Solving for A:
- Thus, A = 45° - 30° = 15°.
Conclusion
The value of A is 15°, confirming that the correct answer is option 'B'. This demonstrates how understanding complementary angles and the properties of tangent can simplify the problem effectively.
sec x + tan x = 2, find the value of cos x- a)1/3
- b)3/4
- c)1/2
- d)4/5
Correct answer is option 'D'. Can you explain this answer?
sec x + tan x = 2, find the value of cos x
a)
1/3
b)
3/4
c)
1/2
d)
4/5
|
|
Ayesha Joshi answered |
Concept:
sec2 x - tan2 x = 1
Calculation:
Given sec x + tan x = 2 ....(i)
∵ sec2 x - tan2 x = 1
(sec x + tan x)(sec x - tan x) = 1
2(sec x - tan x) = 1
sec x - tan x = 1/2 ....(ii)
Adding the equation (i) and (ii)
2 sec x = 2 + 1/2
2/cosx = 5/2
cos x = 4/5
sec2 x - tan2 x = 1
Calculation:
Given sec x + tan x = 2 ....(i)
∵ sec2 x - tan2 x = 1
(sec x + tan x)(sec x - tan x) = 1
2(sec x - tan x) = 1
sec x - tan x = 1/2 ....(ii)
Adding the equation (i) and (ii)
2 sec x = 2 + 1/2
2/cosx = 5/2
cos x = 4/5
If θ is said to be an acute angle, and 4 cos2 θ - 1 = 0, then what is the value of tan (θ - 150)?- a)1
- b)√2
- c)1/√3
- d)None of the above
Correct answer is option 'A'. Can you explain this answer?
If θ is said to be an acute angle, and 4 cos2 θ - 1 = 0, then what is the value of tan (θ - 150)?
a)
1
b)
√2
c)
1/√3
d)
None of the above
|
|
Ayesha Joshi answered |
Given 4 cos2 θ - 1 = 0
4 cos2 θ = 1
cos2 θ = 1/4
cos θ = 1/2
Or, θ = 600
So, tan (θ - 150) = ?
⇒ tan (600 - 150)
= tan 450
= 1
4 cos2 θ = 1
cos2 θ = 1/4
cos θ = 1/2
Or, θ = 600
So, tan (θ - 150) = ?
⇒ tan (600 - 150)
= tan 450
= 1
What is the value of sin 0° + sin 10° + sin 20° + sin 30° + ⋯ + sin 360°?- a)-1
- b)0
- c)1
- d)2
Correct answer is option 'B'. Can you explain this answer?
What is the value of sin 0° + sin 10° + sin 20° + sin 30° + ⋯ + sin 360°?
a)
-1
b)
0
c)
1
d)
2
|
|
Ayesha Joshi answered |
Formula used:
sin(360° - θ) = - sin θ
sin(360° - θ) = - sin θ
Calculation:
sin 0° + sin 10° + sin 20° + sin 30° + ⋯ + sin 360°
⇒ sin 0° + sin 10° + ....+ sin 180° + sin (360 - 170°) + sin (360 - 160°) + .....+ sin (360 - 10°) + sin (360 - 0°)
sin 0° + sin 10° + sin 20° + sin 30° + ⋯ + sin 360°
⇒ sin 0° + sin 10° + ....+ sin 180° + sin (360 - 170°) + sin (360 - 160°) + .....+ sin (360 - 10°) + sin (360 - 0°)
By using the above formula
⇒ sin 0° + sin 10° + ......- sin 10° - sin 0° = 0
∴ sin 0° + sin 10° + sin 20° + sin 30° + ⋯ + sin 360° = 0
⇒ sin 0° + sin 10° + ......- sin 10° - sin 0° = 0
∴ sin 0° + sin 10° + sin 20° + sin 30° + ⋯ + sin 360° = 0
If r cosθ = √3, and r sinθ = 1, what is the value of r2 tanθ?- a)4/√3
- b)√3/4
- c)√3
- d)None of the above
Correct answer is option 'A'. Can you explain this answer?
If r cosθ = √3, and r sinθ = 1, what is the value of r2 tanθ?
a)
4/√3
b)
√3/4
c)
√3
d)
None of the above
|
|
Ayesha Joshi answered |
Given r cosθ = √3, and r sinθ = 1
r cosθ / r sinθ = 1/√3
tanθ = tan 300
Or, θ = 300
On putting, θ = 300, we will get,
r sin 300 = 1
r x ½ = 1
or r =2
Now, r2 tanθ = ?
= (2)2 tan 300
= 4 x 1/√3
= 4/√3
r cosθ / r sinθ = 1/√3
tanθ = tan 300
Or, θ = 300
On putting, θ = 300, we will get,
r sin 300 = 1
r x ½ = 1
or r =2
Now, r2 tanθ = ?
= (2)2 tan 300
= 4 x 1/√3
= 4/√3
If sin θ + cos θ = 7/5, then sinθ cosθ is?- a)11/25
- b)12/25
- c)13/25
- d)14/25
Correct answer is option 'B'. Can you explain this answer?
If sin θ + cos θ = 7/5, then sinθ cosθ is?
a)
11/25
b)
12/25
c)
13/25
d)
14/25

|
Orion Classes answered |
Concept:
sin2 x + cos2 x = 1
Calculation:
Given: sin θ + cos θ = 7/5
By, squaring both sides of the above equation we get,
⇒ (sin θ + cos θ)2 = 49/25
⇒ sin2 θ + cos2 θ + 2sin θ.cos θ = 49/25
As we know that, sin2 x + cos2 x = 1
⇒ 1 + 2sin θcos θ = 49/25
⇒ 2sin θcos θ = 24/25
∴ sin θcos θ = 12/25
sin2 x + cos2 x = 1
Calculation:
Given: sin θ + cos θ = 7/5
By, squaring both sides of the above equation we get,
⇒ (sin θ + cos θ)2 = 49/25
⇒ sin2 θ + cos2 θ + 2sin θ.cos θ = 49/25
As we know that, sin2 x + cos2 x = 1
⇒ 1 + 2sin θcos θ = 49/25
⇒ 2sin θcos θ = 24/25
∴ sin θcos θ = 12/25
If Tan4θ + Tan2θ = 1, then what is the value of Cos4θ + Cos2θ?- a)8
- b)10
- c)1
- d)2
Correct answer is option 'C'. Can you explain this answer?
If Tan4θ + Tan2θ = 1, then what is the value of Cos4θ + Cos2θ?
a)
8
b)
10
c)
1
d)
2
|
|
Ayesha Joshi answered |
Given:
Tan4θ + Tan2θ = 1
Formula:
Sec2θ - Tan2θ = 1
Sin2θ + Cos2θ = 1
Calculation:
Tan4θ + Tan2θ = 1
⇒ Tan2θ (Tan2θ + 1) = 1
⇒ Tan2θ. Sec2θ = 1 {∵ sec2θ = 1 + tan2θ}
⇒ (sin2 θ/cos4 θ) = 1
⇒ 1 – cos2θ = cos4 θ {∵ sin2 θ = 1 – cos2θ}
⇒ cos4 θ + cos2 θ = 1
∴ Then the value of cos4 θ + cos2 θ is 1.
Tan4θ + Tan2θ = 1
Formula:
Sec2θ - Tan2θ = 1
Sin2θ + Cos2θ = 1
Calculation:
Tan4θ + Tan2θ = 1
⇒ Tan2θ (Tan2θ + 1) = 1
⇒ Tan2θ. Sec2θ = 1 {∵ sec2θ = 1 + tan2θ}
⇒ (sin2 θ/cos4 θ) = 1
⇒ 1 – cos2θ = cos4 θ {∵ sin2 θ = 1 – cos2θ}
⇒ cos4 θ + cos2 θ = 1
∴ Then the value of cos4 θ + cos2 θ is 1.
sec4 x - tan4 x is equal to ?- a)1 + tan2 x
- b)2tan2 x - 1
- c)1 + 2tan2 x
- d)None of the above
Correct answer is option 'C'. Can you explain this answer?
sec4 x - tan4 x is equal to ?
a)
1 + tan2 x
b)
2tan2 x - 1
c)
1 + 2tan2 x
d)
None of the above

|
Orion Classes answered |
Concept:
a2 - b2 = (a - b) (a + b)
sec2 x - tan2 x = 1
a2 - b2 = (a - b) (a + b)
sec2 x - tan2 x = 1
Calculation:
sec4 x - tan4 x
=(sec2 x - tan2 x) (sec2 x + tan2 x) (∵ a2 - b2 = (a - b) (a + b))
= 1 × (1 + tan2 x + tan2 x) (∵ sec2 x - tan2 x = 1)
= 1 + 2tan2 x
sec4 x - tan4 x
=(sec2 x - tan2 x) (sec2 x + tan2 x) (∵ a2 - b2 = (a - b) (a + b))
= 1 × (1 + tan2 x + tan2 x) (∵ sec2 x - tan2 x = 1)
= 1 + 2tan2 x
What is the value of (sin 300 + cos 600) - (sin 600 + cos 300)?- a)1 + √2
- b)1 + 2√2
- c)1 + √3
- d)1 + 2√3
Correct answer is option 'C'. Can you explain this answer?
What is the value of (sin 300 + cos 600) - (sin 600 + cos 300)?
a)
1 + √2
b)
1 + 2√2
c)
1 + √3
d)
1 + 2√3
|
|
Anthony Crawford answered |
The value of (sin 300 cos 600) - (sin 600 cos 300) is 1.
The tops of two poles of height 30 m and 14 m are connected by a string. If the wire makes an angle of 30° with the horizontal, find the length of the wire.- a)36 m
- b)34 m
- c)30 m
- d)32 m
Correct answer is option 'D'. Can you explain this answer?
The tops of two poles of height 30 m and 14 m are connected by a string. If the wire makes an angle of 30° with the horizontal, find the length of the wire.
a)
36 m
b)
34 m
c)
30 m
d)
32 m

|
Arshiya Bose answered |
Understanding the Problem
In this problem, we have two poles of different heights (30 m and 14 m) connected by a wire that makes a 30° angle with the horizontal. We need to find the length of this wire.
Step 1: Determine the Height Difference
- Height of the first pole = 30 m
- Height of the second pole = 14 m
- Height difference = 30 m - 14 m = 16 m
Step 2: Visualize the Triangle
- The wire forms the hypotenuse of a right triangle where:
- The vertical side (height difference) = 16 m
- The angle with the horizontal = 30°
Step 3: Use Trigonometric Ratios
- In a right triangle, the sine function relates the opposite side to the hypotenuse:
- sin(θ) = opposite/hypotenuse
- Here, θ = 30° and the opposite side = 16 m.
Step 4: Calculate the Length of the Wire
- Rearranging the sine formula gives us:
- hypotenuse = opposite / sin(θ)
- Plugging in the values:
- hypotenuse = 16 m / sin(30°)
- Since sin(30°) = 1/2:
- hypotenuse = 16 m / (1/2) = 16 m * 2 = 32 m
Conclusion
The length of the wire connecting the tops of the two poles is 32 m, confirming that the correct answer is option D.
In this problem, we have two poles of different heights (30 m and 14 m) connected by a wire that makes a 30° angle with the horizontal. We need to find the length of this wire.
Step 1: Determine the Height Difference
- Height of the first pole = 30 m
- Height of the second pole = 14 m
- Height difference = 30 m - 14 m = 16 m
Step 2: Visualize the Triangle
- The wire forms the hypotenuse of a right triangle where:
- The vertical side (height difference) = 16 m
- The angle with the horizontal = 30°
Step 3: Use Trigonometric Ratios
- In a right triangle, the sine function relates the opposite side to the hypotenuse:
- sin(θ) = opposite/hypotenuse
- Here, θ = 30° and the opposite side = 16 m.
Step 4: Calculate the Length of the Wire
- Rearranging the sine formula gives us:
- hypotenuse = opposite / sin(θ)
- Plugging in the values:
- hypotenuse = 16 m / sin(30°)
- Since sin(30°) = 1/2:
- hypotenuse = 16 m / (1/2) = 16 m * 2 = 32 m
Conclusion
The length of the wire connecting the tops of the two poles is 32 m, confirming that the correct answer is option D.
A right angled triangle has a height ‘p’, base ‘b’ and hypotenuse ‘h’. Which of the following value can h2 not take, given that p and b are positive integers?- a)74
- b)52
- c)13
- d)23
Correct answer is option 'D'. Can you explain this answer?
A right angled triangle has a height ‘p’, base ‘b’ and hypotenuse ‘h’. Which of the following value can h2 not take, given that p and b are positive integers?
a)
74
b)
52
c)
13
d)
23
|
|
Mira Sharma answered |
We know that,
h2 = p2 + b2 Given, p and b are positive integer, so h2 will be sum of two perfect squares.
We see
a) 72 + 52 = 74
b) 62 + 42 = 52
c) 32 + 22 = 13
d) Can’t be expressed as a sum of two perfect squares
h2 = p2 + b2 Given, p and b are positive integer, so h2 will be sum of two perfect squares.
We see
a) 72 + 52 = 74
b) 62 + 42 = 52
c) 32 + 22 = 13
d) Can’t be expressed as a sum of two perfect squares
Therefore the answer is Option D.
If 3 - 4cotθ = cosecθ and 4 + 3cotθ = kcosecθ, find tha value of k- a)4√2
- b)2√6
- c)3√5
- d)3√3
Correct answer is option 'B'. Can you explain this answer?
If 3 - 4cotθ = cosecθ and 4 + 3cotθ = kcosecθ, find tha value of k
a)
4√2
b)
2√6
c)
3√5
d)
3√3
|
|
Ayesha Joshi answered |
Formula:
1 + cot2θ = cosec2θ
1 + cot2θ = cosec2θ
Calculation:
Squaring both equations, we get-
⇒ (3 - 4cot)2 = (cosecθ)2
⇒ 9 + 16cot2θ - 2 × 3 × 4cotθ = cosec2θ
⇒ 9 + 16cot2θ - 24cotθ = cosec2θ (Eq 1)
Similarly,
⇒ (4 + 3cotθ)2 = (kcosecθ)2
⇒ 16 + 9cot2θ + 2 × 4 × 3cotθ = k2cosec2θ
⇒ 16 + 9cot2θ + 24cotθ = k2cosec2θ (Eq 2)
Adding Eq 1 and Eq 2, we get-
⇒ 9 + 16cot2θ - 24cotθ + 16 + 9cot2θ + 24cotθ = cosec2θ + k2cosec2θ
⇒ 25 + 25cot2θ = cosec2θ (1 + k2)
⇒ 25 (1 + cot2θ) = cosec2θ (1 + k2)
Substituting the value of 1 + cot2θ as cosec2θ, we get-
⇒ 25 × cosec2θ = cosec2θ (1 + k2)
⇒ 25 = 1 + k2
∴ k2 = 24 or k = 2√6
The value of k is 2√6
Squaring both equations, we get-
⇒ (3 - 4cot)2 = (cosecθ)2
⇒ 9 + 16cot2θ - 2 × 3 × 4cotθ = cosec2θ
⇒ 9 + 16cot2θ - 24cotθ = cosec2θ (Eq 1)
Similarly,
⇒ (4 + 3cotθ)2 = (kcosecθ)2
⇒ 16 + 9cot2θ + 2 × 4 × 3cotθ = k2cosec2θ
⇒ 16 + 9cot2θ + 24cotθ = k2cosec2θ (Eq 2)
Adding Eq 1 and Eq 2, we get-
⇒ 9 + 16cot2θ - 24cotθ + 16 + 9cot2θ + 24cotθ = cosec2θ + k2cosec2θ
⇒ 25 + 25cot2θ = cosec2θ (1 + k2)
⇒ 25 (1 + cot2θ) = cosec2θ (1 + k2)
Substituting the value of 1 + cot2θ as cosec2θ, we get-
⇒ 25 × cosec2θ = cosec2θ (1 + k2)
⇒ 25 = 1 + k2
∴ k2 = 24 or k = 2√6
The value of k is 2√6
If Cos x – Sin x = √2 Sin x, find the value of Cos x + Sin x:- a)√2 Cos x
- b)√2 Cosec x
- c)√2 Sec x
- d)√2 Sin x Cos x
Correct answer is option 'A'. Can you explain this answer?
If Cos x – Sin x = √2 Sin x, find the value of Cos x + Sin x:
a)
√2 Cos x
b)
√2 Cosec x
c)
√2 Sec x
d)
√2 Sin x Cos x
|
|
Mira Sharma answered |
Cos x – Sin x = √2 Sin x
=> Cos x = Sin x + √2 Sin x
=> Cos x = Sin x + √2 Sin x
=> Sin x = Cosx/(√2+1) * Cos x
=> Sin x = (√2−1)/(√2−1) * 1/(√2+1) * Cos x
=> Sin x = (√2−1)/((√2)2−(1)2)* Cos x
=> Sin x = (√2 - 1) Cos x
=> Sin x = √2 Cos x – Cos x
=> Sin x + Cos x = √2 Cos x
=> Cos x = Sin x + √2 Sin x
=> Cos x = Sin x + √2 Sin x
=> Sin x = Cosx/(√2+1) * Cos x
=> Sin x = (√2−1)/(√2−1) * 1/(√2+1) * Cos x
=> Sin x = (√2−1)/((√2)2−(1)2)* Cos x
=> Sin x = (√2 - 1) Cos x
=> Sin x = √2 Cos x – Cos x
=> Sin x + Cos x = √2 Cos x
Hence, the correct answer is Option A.
If θ is said to be an acute angle, and 7 sin2 θ + 3 cos2 θ = 4, then what is the value of tan θ?- a)1
- b)√3
- c)1/√3
- d)None of the above
Correct answer is option 'C'. Can you explain this answer?
If θ is said to be an acute angle, and 7 sin2 θ + 3 cos2 θ = 4, then what is the value of tan θ?
a)
1
b)
√3
c)
1/√3
d)
None of the above
|
|
Ayesha Joshi answered |
Given 7 sin2 θ + 3 cos2 θ = 4
=> 7 sin2 θ + 3 (1 - sin2 θ) = 4
=> 7 sin2 θ + 3 - 3sin2 θ = 4
Then, 4sin2 θ = 1
Or, sin θ = 1/2
So, θ = 300
Now, put θ = 300 in tan θ, we will get,
tan θ = 1/√3
=> 7 sin2 θ + 3 (1 - sin2 θ) = 4
=> 7 sin2 θ + 3 - 3sin2 θ = 4
Then, 4sin2 θ = 1
Or, sin θ = 1/2
So, θ = 300
Now, put θ = 300 in tan θ, we will get,
tan θ = 1/√3
Alternate
We can directly check the equation by putting values of θ. Let's put θ = 300
7 sin2 300 + 3 cos2 300= 4
Then, 7 * 1/4 + 3 * 3/4 = 4
So, 7/4 + 9/4 = 4
16/4 = 4
Or, 4 = 4 (so, it satisfy the condition)
Now, tan 300 = 1/√3
We can directly check the equation by putting values of θ. Let's put θ = 300
7 sin2 300 + 3 cos2 300= 4
Then, 7 * 1/4 + 3 * 3/4 = 4
So, 7/4 + 9/4 = 4
16/4 = 4
Or, 4 = 4 (so, it satisfy the condition)
Now, tan 300 = 1/√3
Chapter doubts & questions for Trigonometry - Mathematics for ACT 2025 is part of ACT exam preparation. The chapters have been prepared according to the ACT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for ACT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Trigonometry - Mathematics for ACT in English & Hindi are available as part of ACT exam.
Download more important topics, notes, lectures and mock test series for ACT Exam by signing up for free.
Mathematics for ACT
144 videos|100 docs|61 tests
|
Signup to see your scores go up within 7 days!
Study with 1000+ FREE Docs, Videos & Tests
10M+ students study on EduRev

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup