All Exams >
Year 12 >
Mathematics for Year 12 >
All Questions
All questions of Conic sections for Year 12 Exam
The angle between the two tangents from the origin to the circle (x – 7)2 + (y + 1)2 = 25 equals- a)π/2
- b)π/3
- c)π/4
- d)None
Correct answer is option 'A'. Can you explain this answer?
The angle between the two tangents from the origin to the circle (x – 7)2 + (y + 1)2 = 25 equals
a)
π/2
b)
π/3
c)
π/4
d)
None
|
Aryan Singh answered |
To find the angle between the two tangents from the origin to the circle, we can use the fact that the angle between a tangent and a radius at the point of tangency is always 90 degrees.
Let's assume the coordinates of the center of the circle are (h, k) and the radius is r.
The equation of the circle is given by:
(x - h)^2 + (y - k)^2 = r^2
Since the origin is (0, 0), the equation of the line passing through the origin and the center of the circle can be written as:
(y - k) = m(x - h)
Substituting x = 0 and y = 0, we get:
(-k) = mh
Simplifying, we get:
m = -k/h
The slope of a line perpendicular to m is the negative reciprocal of m. So, the slope of the tangent lines is:
m_perpendicular = -1/m = -1/(-k/h) = h/k
The angle between the two tangents can be found using the formula for the angle between two lines with slopes m1 and m2:
tan(theta) = |(m1 - m2) / (1 + m1 * m2)|
Substituting m1 = h/k and m2 = -h/k, we get:
tan(theta) = |(h/k + h/k) / (1 + h/k * -h/k)| = |(2h/k) / (1 - (h^2/k^2))|
Simplifying, we get:
tan(theta) = |(2h/k) / ((k^2 - h^2)/k^2)| = |2h / (k^2 - h^2)|
Therefore, the angle between the two tangents from the origin to the circle is given by:
theta = atan(|2h / (k^2 - h^2)|)
Let's assume the coordinates of the center of the circle are (h, k) and the radius is r.
The equation of the circle is given by:
(x - h)^2 + (y - k)^2 = r^2
Since the origin is (0, 0), the equation of the line passing through the origin and the center of the circle can be written as:
(y - k) = m(x - h)
Substituting x = 0 and y = 0, we get:
(-k) = mh
Simplifying, we get:
m = -k/h
The slope of a line perpendicular to m is the negative reciprocal of m. So, the slope of the tangent lines is:
m_perpendicular = -1/m = -1/(-k/h) = h/k
The angle between the two tangents can be found using the formula for the angle between two lines with slopes m1 and m2:
tan(theta) = |(m1 - m2) / (1 + m1 * m2)|
Substituting m1 = h/k and m2 = -h/k, we get:
tan(theta) = |(h/k + h/k) / (1 + h/k * -h/k)| = |(2h/k) / (1 - (h^2/k^2))|
Simplifying, we get:
tan(theta) = |(2h/k) / ((k^2 - h^2)/k^2)| = |2h / (k^2 - h^2)|
Therefore, the angle between the two tangents from the origin to the circle is given by:
theta = atan(|2h / (k^2 - h^2)|)
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Point (-2, – 5) lies on the circle x2 + y2 = 25.- a)On the axis outside the circle
- b)Outside
- c)Inside
- d)On the circle
Correct answer is option 'B'. Can you explain this answer?
Point (-2, – 5) lies on the circle x2 + y2 = 25.
a)
On the axis outside the circle
b)
Outside
c)
Inside
d)
On the circle
|
Hansa Sharma answered |
X2 +Y2 =25 Points =(-2,-5)
Put the points in the variables
(-2)2 + (-5)2 = 29
As 29 > 25 (lies outside).
Put the points in the variables
(-2)2 + (-5)2 = 29
As 29 > 25 (lies outside).
The radius of the circle given by 2x2 + 2y2 – x = 0 is- a)1/4
- b)1
- c)2
- d)1/2
Correct answer is option 'A'. Can you explain this answer?
The radius of the circle given by 2x2 + 2y2 – x = 0 is
a)
1/4
b)
1
c)
2
d)
1/2
|
Geetika Shah answered |
2x² + 2y² - x = 0 .
==> 2 ( x² + y² - x/2 ) = 0 .
==> 2/2 ( x² + y² - x/2 ) = 0/2 .
==> x² - x/2 + y² = 0 .
==> ( x² - x/2 + (1/4)² ) + y² = (1/4)² .
==> ( x - 1/4 )² + ( y - 0 )² = (1/4)²
Centre (-¼, 0) radius(¼)
==> 2 ( x² + y² - x/2 ) = 0 .
==> 2/2 ( x² + y² - x/2 ) = 0/2 .
==> x² - x/2 + y² = 0 .
==> ( x² - x/2 + (1/4)² ) + y² = (1/4)² .
==> ( x - 1/4 )² + ( y - 0 )² = (1/4)²
Centre (-¼, 0) radius(¼)
The equation of circle whose centre is (2, 1) and which passes through the point (3, – 5) is:- a)
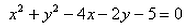
- b)
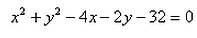
- c)
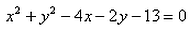
- d)
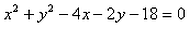
Correct answer is option 'B'. Can you explain this answer?
The equation of circle whose centre is (2, 1) and which passes through the point (3, – 5) is:
a)
b)
c)
d)
|
Poonam Reddy answered |
Radius of circle is given by -
r = √[(h-x1)² + (k-y1)²]
r = √[(2-3)² + (1+5)²]
r = √(-1² + 6²)
r = √(1 + 36)
r = √37
if centre (2,-]1) and radius=√26 are given,
(x-h)2+(y-k)2=r2
equation is (x-2)2 + (y-1)2 = (√37)2
x2 + 4 - 4x + y2 + 1 - 2y = 37
x2 + y2 - 4x - 2y - 32 = 0
r = √[(h-x1)² + (k-y1)²]
r = √[(2-3)² + (1+5)²]
r = √(-1² + 6²)
r = √(1 + 36)
r = √37
if centre (2,-]1) and radius=√26 are given,
(x-h)2+(y-k)2=r2
equation is (x-2)2 + (y-1)2 = (√37)2
x2 + 4 - 4x + y2 + 1 - 2y = 37
x2 + y2 - 4x - 2y - 32 = 0
The equation of circle of radius 5 units touches the coordinates axes in the second quadrant is:- a)x2 + y2 + 10x – 10y + 25 = 0
- b)x2 + y2 – 10x – 10y + 25 = 0
- c)x2 + y2 + 10x + 10y + 25 = 0
- d)x2 + y2 – 10x – 10y – 25 = 0
Correct answer is option 'A'. Can you explain this answer?
The equation of circle of radius 5 units touches the coordinates axes in the second quadrant is:
a)
x2 + y2 + 10x – 10y + 25 = 0
b)
x2 + y2 – 10x – 10y + 25 = 0
c)
x2 + y2 + 10x + 10y + 25 = 0
d)
x2 + y2 – 10x – 10y – 25 = 0
|
Suresh Reddy answered |
If the circle lies in second quadrant
The equation of a circle touches both the coordinate axes and has radius a is
x2 + y2 + 2ax - 2ay + a2 = 0
Radius of circle, a = 5
x2 + y2 + 10x - 10y + 25 = 0
The equation of a circle touches both the coordinate axes and has radius a is
x2 + y2 + 2ax - 2ay + a2 = 0
Radius of circle, a = 5
x2 + y2 + 10x - 10y + 25 = 0
The centre of the ellipse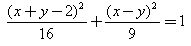 
is:- a)(0, 1)
- b)(1, 1)
- c)(0, 0)
- d)(1, 0)
Correct answer is option 'B'. Can you explain this answer?
The centre of the ellipse 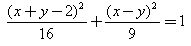is:
is:a)
(0, 1)
b)
(1, 1)
c)
(0, 0)
d)
(1, 0)
|
|
Preeti Iyer answered |
Centre of the ellipse is the intersection point of
x+y−1=0.........(1)
x−y=0............(2)
Substituting x from equation 2 in equation 1 two equations, we get,
2y=2, y=1
Replacing, we get x=1
⇒(1,1) is the centre
x+y−1=0.........(1)
x−y=0............(2)
Substituting x from equation 2 in equation 1 two equations, we get,
2y=2, y=1
Replacing, we get x=1
⇒(1,1) is the centre
The equation of the ellipse whose one focus is at (4, 0) and whose eccentricity is 4/5 is:- a)
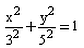
- b)
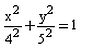
- c)
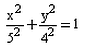
- d)
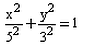
Correct answer is option 'D'. Can you explain this answer?
The equation of the ellipse whose one focus is at (4, 0) and whose eccentricity is 4/5 is:
a)
b)
c)
d)
|
Neha Sharma answered |
focus lies on x axis
So, the equation of ellipse is x2/a2 + y2/b2 = 1
Co-ordinate of focus(+-ae, 0)
ae = 4
e = ⅘
a = 4/e => 4/(⅘)
a = 5
(a)2 = 25
b2 = a2(1-e2)
= 25(1-16/25)
b2 = 9
Required equation : x2/(5)2 + y2/(3)2 = 1
So, the equation of ellipse is x2/a2 + y2/b2 = 1
Co-ordinate of focus(+-ae, 0)
ae = 4
e = ⅘
a = 4/e => 4/(⅘)
a = 5
(a)2 = 25
b2 = a2(1-e2)
= 25(1-16/25)
b2 = 9
Required equation : x2/(5)2 + y2/(3)2 = 1
The asymptotes of the hyperbola xy–3x–2y = 0 are- a)x – 2 = 0 and y – 3 = 0
- b)x – 3 = 0 and y – 2 = 0
- c)x + 2 = 0 and y + 3 = 0
- d)x +3 = 0 and y + 2 = 0
Correct answer is option 'A'. Can you explain this answer?
The asymptotes of the hyperbola xy–3x–2y = 0 are
a)
x – 2 = 0 and y – 3 = 0
b)
x – 3 = 0 and y – 2 = 0
c)
x + 2 = 0 and y + 3 = 0
d)
x +3 = 0 and y + 2 = 0
|
|
Suresh Reddy answered |
xy - 3x - 2y + λ = 0.
Then abc + 2fgh − af2 − bg2 − ch2 = 0
⇒ 3/2 − λ/4 = 0
⇒ λ = 6
∴ Equation of asymptotes is xy-3x-2y+6=0
⇒ (x-2)(y-3)=0
⇒x - 2 = 0 and y - 3 = 0
Then abc + 2fgh − af2 − bg2 − ch2 = 0
⇒ 3/2 − λ/4 = 0
⇒ λ = 6
∴ Equation of asymptotes is xy-3x-2y+6=0
⇒ (x-2)(y-3)=0
⇒x - 2 = 0 and y - 3 = 0
A circle is the set of …… in a plane that are equidistant from a fixed point in the plane.- a)Points
- b)Lines
- c)Cones
- d)Circles
Correct answer is option 'B'. Can you explain this answer?
A circle is the set of …… in a plane that are equidistant from a fixed point in the plane.
a)
Points
b)
Lines
c)
Cones
d)
Circles
|
|
Mira Sharma answered |
The correct answer is a.
A circle is the set of all points in a plane that are equidistant from a given point called the center of the circle. We use the symbol to represent a circle.
+ 
= 1, and its corresponding point Q on the auxiliary circle meet on the line
The equation of the tangent lines to the hyperbola x2 – 2y2 = 18 which are perpendicular to the line y = x are- a)y = x ± 3
- b)y = –x ± 3
- c)2x + 3y + 4 = 0
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
The equation of the tangent lines to the hyperbola x2 – 2y2 = 18 which are perpendicular to the line y = x are
a)
y = x ± 3
b)
y = –x ± 3
c)
2x + 3y + 4 = 0
d)
None of these
|
|
Preeti Khanna answered |
Equation of line perpendicular to x−y=0 is given by
y=−x+c
Also this line is tangent to the hyperbola x2−2y2=18
So we have m=−1, a2=18, b2=9
Thus Using condition of tangency c2 = a2m2−b2
= 18−9=9
⇒ c = ±3
Hence required equation of tangent is x+y = ±3
y=−x+c
Also this line is tangent to the hyperbola x2−2y2=18
So we have m=−1, a2=18, b2=9
Thus Using condition of tangency c2 = a2m2−b2
= 18−9=9
⇒ c = ±3
Hence required equation of tangent is x+y = ±3
The equation of the circle passing through (0, 0) and making intercepts 2 and 4 on the coordinate axes is:- a)
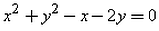
- b)
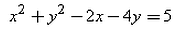
- c)
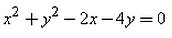
- d)
Correct answer is option 'C'. Can you explain this answer?
The equation of the circle passing through (0, 0) and making intercepts 2 and 4 on the coordinate axes is:
a)
b)
c)
d)
|
|
Geetika Shah answered |
The circle intercept the co-ordinate axes at a and b. it means x - intercept at ( a, 0) and y-intercept at (0, b) .
Now, we observed that circle passes through points (0, 0) , (a, 0) and (0, b) .
we also know, General equation of circle is
x² + y² + 2gx + 2fy + C = 0
when point (0,0)
(0)² + (0)² + 2g(0) + 2f(0) + C = 0
0 + 0 + 0 + 0 + C = 0
C = 0 -------(1)
when point (a,0)
(a)² + (0)² + 2g(a) + 2f(0) + C = 0
a² + 2ag + C = 0
from equation (1)
a² + 2ag = 0
a(a + 2g) = 0
g = -a/2
when point ( 0, b)
(0)² + (b)² + 2g(0) + 2f(b) + C = 0
b² + 2fb + C = 0
f = -b/2
Now, equation of circle is
x² + y² + 2x(-a/2) + 2y(-b/2) + 0 = 0 { after putting values of g, f and C }
x² + y² - ax - by = 0
As we know that, a=2, b=4
x^2 + y^2 - 2x - 4y = 0
Now, we observed that circle passes through points (0, 0) , (a, 0) and (0, b) .
we also know, General equation of circle is
x² + y² + 2gx + 2fy + C = 0
when point (0,0)
(0)² + (0)² + 2g(0) + 2f(0) + C = 0
0 + 0 + 0 + 0 + C = 0
C = 0 -------(1)
when point (a,0)
(a)² + (0)² + 2g(a) + 2f(0) + C = 0
a² + 2ag + C = 0
from equation (1)
a² + 2ag = 0
a(a + 2g) = 0
g = -a/2
when point ( 0, b)
(0)² + (b)² + 2g(0) + 2f(b) + C = 0
b² + 2fb + C = 0
f = -b/2
Now, equation of circle is
x² + y² + 2x(-a/2) + 2y(-b/2) + 0 = 0 { after putting values of g, f and C }
x² + y² - ax - by = 0
As we know that, a=2, b=4
x^2 + y^2 - 2x - 4y = 0
The eccentricity of an ellipse whose latus rectum is equal to distance between foci is:- a)
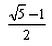
- b)
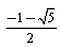
- c)
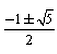
- d)
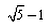
Correct answer is option 'A'. Can you explain this answer?
The eccentricity of an ellipse whose latus rectum is equal to distance between foci is:
a)
b)
c)
d)
|
|
Suresh Reddy answered |
Distance between the foci of an ellipse = length of latus rectum
i.e. (2b2)/a=2ae
e=b2/a2
But e=[1−b2/a2]1/2
Then e=(1−e)1/2
Squaring both sides, we get
e2 +e−1=0
e=−1 ± (1 + 4)1/2]/2
(∵ Eccentricity cannot be negative)
e=[(5)1/2 − 1]/2
i.e. (2b2)/a=2ae
e=b2/a2
But e=[1−b2/a2]1/2
Then e=(1−e)1/2
Squaring both sides, we get
e2 +e−1=0
e=−1 ± (1 + 4)1/2]/2
(∵ Eccentricity cannot be negative)
e=[(5)1/2 − 1]/2
If distance between the directrices be thrice the distance between the foci, then eccentricity of ellipse is- a)
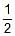
- b)
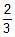
- c)
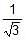
- d)
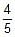
Correct answer is option 'C'. Can you explain this answer?
If distance between the directrices be thrice the distance between the foci, then eccentricity of ellipse is
a)
b)
c)
d)
|
|
Neha Sharma answered |
Distance between the directrices is 2a/e
Distance between the foci is 2ae
Given: 2a/e = 3∗2ae
Or,e2 = 1/3
∴ e=1/√3
Distance between the foci is 2ae
Given: 2a/e = 3∗2ae
Or,e2 = 1/3
∴ e=1/√3
The centre and radius of the circle x2 + y2 + 4x – 6y = 5 is:- a)(2, – 3), 2√2
- b)(– 2, 3), 3√2
- c)(– 2, 3), 2√2
- d)(2, – 3), 3√2
Correct answer is option 'B'. Can you explain this answer?
The centre and radius of the circle x2 + y2 + 4x – 6y = 5 is:
a)
(2, – 3), 2√2
b)
(– 2, 3), 3√2
c)
(– 2, 3), 2√2
d)
(2, – 3), 3√2
|
Riya Banerjee answered |
x2+y2+4x-6y=5
Circle Equation
(x-a)2+(y-b)2=r2 is the circle equation with a radius r, centered at (a,b)
Rewrite x2+y24x-6y=5 in the form of circle standard circle equation
(x-(-2))
Therefore the circle properties are:
(a,b) = (-2,3), r = 3√2
Circle Equation
(x-a)2+(y-b)2=r2 is the circle equation with a radius r, centered at (a,b)
Rewrite x2+y24x-6y=5 in the form of circle standard circle equation
(x-(-2))
2
+(y-3)2=(3
√2)2Therefore the circle properties are:
(a,b) = (-2,3), r = 3√2
A tangent having slope of _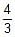
to the ellipse
+ 
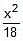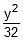= 1 intersects the major & minor axes in points A & B respectively. If C is the centre of the ellipse then the area of the triangle ABC is- a)12 sq. units
- b)24 sq. units
- c)36 sq. units
- d)48 sq. units
Correct answer is option 'B'. Can you explain this answer?
A tangent having slope of _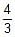 to the ellipse
to the ellipse + = 1 intersects the major & minor axes in points A & B respectively. If C is the centre of the ellipse then the area of the triangle ABC isa)
12 sq. units
b)
24 sq. units
c)
36 sq. units
d)
48 sq. units
|
|
Preeti Khanna answered |
Since the major axis is along the y-axis.
∴ Equation of tangent is x = my + [b2m2 + a]1/2
Slope of tangent = 1/m = −4/3
⇒ m = −3/4
Hence, equation of tangent is 4x+3y=24 or
x/6 + y/8 = 1
Its intercepts on the axes are 6 and 8.
Area (ΔAOB) = 1/2×6×8
= 24 sq. unit
∴ Equation of tangent is x = my + [b2m2 + a]1/2
Slope of tangent = 1/m = −4/3
⇒ m = −3/4
Hence, equation of tangent is 4x+3y=24 or
x/6 + y/8 = 1
Its intercepts on the axes are 6 and 8.
Area (ΔAOB) = 1/2×6×8
= 24 sq. unit
The equation of a circle which is concentric to the given circle x2 + y2 - 4x - 6y - 3 = 0 and which touches the Y-axis is:
- a)x2 + y2 + 4x + 6y + 13 = 0
- b)x2 + y2 - 4x - 6y + 13 = 0
- c)x2 + y2 - 4x - 6y + 9 = 0
- d)x2 + y2 - 4x - 6y + 4 = 0
Correct answer is option 'C'. Can you explain this answer?
The equation of a circle which is concentric to the given circle x2 + y2 - 4x - 6y - 3 = 0 and which touches the Y-axis is:
a)
x2 + y2 + 4x + 6y + 13 = 0
b)
x2 + y2 - 4x - 6y + 13 = 0
c)
x2 + y2 - 4x - 6y + 9 = 0
d)
x2 + y2 - 4x - 6y + 4 = 0
|
Aryan Khanna answered |
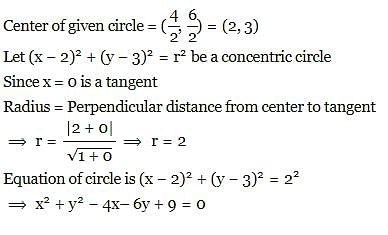
Foot of normals drawn from the point p(h,k) to the hyperbola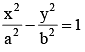 
will always lie on the conic- a)
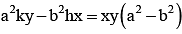
- b)
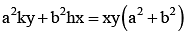
- c)
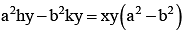
- d)
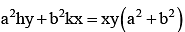
Correct answer is option 'D'. Can you explain this answer?
Foot of normals drawn from the point p(h,k) to the hyperbola 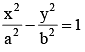will always lie on the conic
will always lie on the conica)
b)
c)
d)
|
Vijay Kumar answered |
Equation of normal at any point (x1, y1) is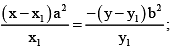 
it passes through
P (h, k) then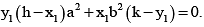
thus (x1, y1) lie on the conic
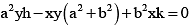
it passes through P (h, k) then
thus (x1, y1) lie on the conic Equation of the chord of the hyperbola 25x2 – 16y2 = 400 which is bisected at the point (6, 2) is- a)16x – 75y = 418
- b)75x – 16y = 418
- c)25x – 4y = 400
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
Equation of the chord of the hyperbola 25x2 – 16y2 = 400 which is bisected at the point (6, 2) is
a)
16x – 75y = 418
b)
75x – 16y = 418
c)
25x – 4y = 400
d)
None of these
|
|
Hansa Sharma answered |
Given hyperbola is 25x2−16y2=400
If (6, 2) is the midpoint of the chord, then equation of chord is T = S1
⇒25(6x)−16(2y)=25(36)−16(4)
⇒75x−16y=450−32
⇒75x−16y=418
If (6, 2) is the midpoint of the chord, then equation of chord is T = S1
⇒25(6x)−16(2y)=25(36)−16(4)
⇒75x−16y=450−32
⇒75x−16y=418
The locus of the mid-points of the chords of the circle x2 + y2 – 2x – 4y – 11 = 0 which subtend 60º at the centre is- a)x2 + y2 – 4x – 2y – 7 = 0
- b)x2 + y2 + 4x + 2y – 7 = 0
- c)x2 + y2 – 2x – 4y – 7 = 0
- d)x2 + y2 + 2x + 4y + 7 = 0
Correct answer is option 'C'. Can you explain this answer?
The locus of the mid-points of the chords of the circle x2 + y2 – 2x – 4y – 11 = 0 which subtend 60º at the centre is
a)
x2 + y2 – 4x – 2y – 7 = 0
b)
x2 + y2 + 4x + 2y – 7 = 0
c)
x2 + y2 – 2x – 4y – 7 = 0
d)
x2 + y2 + 2x + 4y + 7 = 0
|
|
Preeti Iyer answered |
Let AB be the chord of the circle and P be the midpoint of AB.
It is known that perpendicular from the center bisects a chord.
Thus △ACP is a right-angled triangle.
Now AC=BC= radius.
The equation of the give circle can be written as
(x−1)2+(y−2)2=16
Hence, centre C=(1,2) and radius =r=4 units.
PC=ACsin60degree
= rsin60degree
= 4([2(3)½]/2
= 2(3)1/2 units
Therefore, PC=2(3)1/2
⇒ PC2=12
⇒ (x−1)2+(y−2)2=12
⇒ x2+y2−2x−4y+5=12
⇒ x2+y2−2x−4y−7=0
It is known that perpendicular from the center bisects a chord.
Thus △ACP is a right-angled triangle.
Now AC=BC= radius.
The equation of the give circle can be written as
(x−1)2+(y−2)2=16
Hence, centre C=(1,2) and radius =r=4 units.
PC=ACsin60degree
= rsin60degree
= 4([2(3)½]/2
= 2(3)1/2 units
Therefore, PC=2(3)1/2
⇒ PC2=12
⇒ (x−1)2+(y−2)2=12
⇒ x2+y2−2x−4y+5=12
⇒ x2+y2−2x−4y−7=0
The number of common tangents of the circles x2 + y2 – 2x – 1 = 0 and x2 + y2 – 2y – 7 = 0- a)1
- b)2
- c)3
- d)4
Correct answer is option 'A'. Can you explain this answer?
The number of common tangents of the circles x2 + y2 – 2x – 1 = 0 and x2 + y2 – 2y – 7 = 0
a)
1
b)
2
c)
3
d)
4
|
|
Neha Joshi answered |
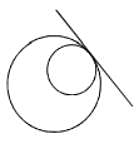
Internally touch ∴ common tangent is one.
Any point on the parabola whose focus is (0,1) and the directrix is x + 2 = 0 is given by- a)(t2 + 1, 2t – 1)
- b)(t2, 2t)
- c)(t2 + 1, 2t + 1)
- d)(t2 – 1, 2t + 1)
Correct answer is option 'D'. Can you explain this answer?
Any point on the parabola whose focus is (0,1) and the directrix is x + 2 = 0 is given by
a)
(t2 + 1, 2t – 1)
b)
(t2, 2t)
c)
(t2 + 1, 2t + 1)
d)
(t2 – 1, 2t + 1)
|
|
Pooja Shah answered |
f(0,1),d(x+2=0)
Distance of any point on parabola and focus is equal to distance of point and directrix.
fP=(h−0)2+(k−1)2= (h2+k2+1−2k)1/2
Distance of point (h,k) and line x+2=0
Using point line distance formula.
dP=h+2
[h2+k2+1−2k]1/2=h+2
h2+k2+1−2k = h2+4+4h
k2−2k+1−4−4h=0
replacing h→x,k→y y2−2y+1−4−4x=0
(y−1)2=4(x+1) …(1)
Let Y=y−1,X=x+1 then (1) becomes
Y^2=4aX2
Here a=1 any point on this parabola will be of the form (at2,2at)=(t2,2at)
⇒X=t2 ⇒x+1=t2
⇒x=t2−1
⇒Y2=2t
⇒y−1 = 2t ⇒ y = 2t+1
∴ Any point on the parabola (y−1)2=4(x+1) is
= (t2−1,2t+1)
Distance of any point on parabola and focus is equal to distance of point and directrix.
fP=(h−0)2+(k−1)2= (h2+k2+1−2k)1/2
Distance of point (h,k) and line x+2=0
Using point line distance formula.
dP=h+2
[h2+k2+1−2k]1/2=h+2
h2+k2+1−2k = h2+4+4h
k2−2k+1−4−4h=0
replacing h→x,k→y y2−2y+1−4−4x=0
(y−1)2=4(x+1) …(1)
Let Y=y−1,X=x+1 then (1) becomes
Y^2=4aX2
Here a=1 any point on this parabola will be of the form (at2,2at)=(t2,2at)
⇒X=t2 ⇒x+1=t2
⇒x=t2−1
⇒Y2=2t
⇒y−1 = 2t ⇒ y = 2t+1
∴ Any point on the parabola (y−1)2=4(x+1) is
= (t2−1,2t+1)
From the focus of the parabola y2 = 8x as centre, a circle is described so that a common chord of the curves is equidistant from the vertex and focus of the parabola. The equation of the circle is- a) (x – 2)2 + y2 = 3
- b) (x – 2)2 + y2 = 9
- c)(x + 2)2 + y2 = 9
- d)None
Correct answer is option 'B'. Can you explain this answer?
From the focus of the parabola y2 = 8x as centre, a circle is described so that a common chord of the curves is equidistant from the vertex and focus of the parabola. The equation of the circle is
a)
(x – 2)2 + y2 = 3
b)
(x – 2)2 + y2 = 9
c)
(x + 2)2 + y2 = 9
d)
None
|
|
Geetika Shah answered |
Focus of parabola y2 = 8x is (2,0). Equation of circle with centre (2,0) is (x−2)2 + y2 = r2
Let AB is common chord and Q is mid point i.e. (1,0)
AQ2 = y2 = 8x
= 8×1 = 8
∴ r2 = AQ2 + QS2
= 8 + 1 = 9
So required circle is (x−2)2 + y2 = 9
Let AB is common chord and Q is mid point i.e. (1,0)
AQ2 = y2 = 8x
= 8×1 = 8
∴ r2 = AQ2 + QS2
= 8 + 1 = 9
So required circle is (x−2)2 + y2 = 9
A parabola whose axis is along the y-axis, vertex is (0,0) and point from the first and second quadrants lie on it, has the equation of the type- a)
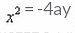
- b)
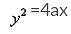
- c)
- d)
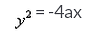
Correct answer is option 'C'. Can you explain this answer?
A parabola whose axis is along the y-axis, vertex is (0,0) and point from the first and second quadrants lie on it, has the equation of the type
a)
b)
c)
d)
|
|
Rohini Verma answered |
As the quadrants lies in first and second quadrant
y = -a Focus(0,a)
x2 = 4ay
y = -a Focus(0,a)
x2 = 4ay
y = √3x + c1 & y = √3x + c2 are two parallel tangents of a circle of radius 2 units, then |c1 – c2| is equal to
- a)8
- b)4
- c)2
- d)1
Correct answer is option 'A'. Can you explain this answer?
y = √3x + c1 & y = √3x + c2 are two parallel tangents of a circle of radius 2 units, then |c1 – c2| is equal to
a)
8
b)
4
c)
2
d)
1
|
|
Anmol Chauhan answered |
For both lines to be parallel tangent the distance between both lines
should be equal to the diameter of the circle
⇒ 4 = |c1−c2|/(1+3)1/2
⇒∣c1−c2∣ = 8
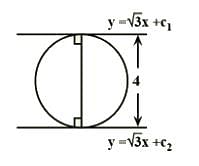
should be equal to the diameter of the circle
⇒ 4 = |c1−c2|/(1+3)1/2
⇒∣c1−c2∣ = 8
If y=c is a tangent to the circle x2+y2–2x+2y–2 =0 at (1, 1), then the value of c is- a)1
- b)2
- c)–1
- d)–2
Correct answer is option 'A'. Can you explain this answer?
If y=c is a tangent to the circle x2+y2–2x+2y–2 =0 at (1, 1), then the value of c is
a)
1
b)
2
c)
–1
d)
–2
|
|
Raghav Bansal answered |
For line y=c to be tangent to the given circle at point (1,1)
It has to pass through (1,1)
⇒ c = 1
It has to pass through (1,1)
⇒ c = 1
The equation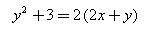 
represents a parabola with the vertex at- a)
- b)
- c)
- d)
Correct answer is option 'C'. Can you explain this answer?
The equation 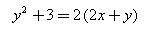represents a parabola with the vertex at
represents a parabola with the vertex ata)
b)
c)
d)
|
|
Gaurav Kumar answered |
y2+3=2(2x+y) represents parabola.
y2+3=4x+2y
y2−2y+3=4x
y2−2y+1+3=4x+1
(y−1)2=4x−2
(y−1)2=4(x−1/2)
So, the vertex of parabola=(1/2,1) and axis is parallel to x axis.
a=1
Focus=(1/2+1,1)
=(3/2,1)
y2+3=4x+2y
y2−2y+3=4x
y2−2y+1+3=4x+1
(y−1)2=4x−2
(y−1)2=4(x−1/2)
So, the vertex of parabola=(1/2,1) and axis is parallel to x axis.
a=1
Focus=(1/2+1,1)
=(3/2,1)
The length of the semi-latus-rectum of an ellipse is one third of its major axis, its eccentricity would be
- a)
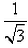
- b)
- c)2/3
- d)
Correct answer is option 'A'. Can you explain this answer?
The length of the semi-latus-rectum of an ellipse is one third of its major axis, its eccentricity would be
a)
b)
c)
2/3
d)
|
|
Suresh Iyer answered |
Correct Answer :- a
Explanation : Semi latus rectum of ellipse = one half the last rectum
b2/a = 1/3*2a
b2 = 2a2/3
b = (2a/3)1/2...........(1)
So, b2/a = a(1-e2)
b2 = a2(1-e2)
Substituting from (1)
2a2/3 = a2(1-e2)
e2 = 1-2/3
e2 = 1/(3)1/2
The line 4x – 7y + 10 = 0 intersects the parabola, y2 = 4x at the points A & B. The co-ordinates of the point of intersection of the tangents drawn at the points A & B are- a)
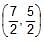
- b)
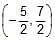
- c)
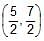
- d)
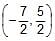
Correct answer is option 'C'. Can you explain this answer?
The line 4x – 7y + 10 = 0 intersects the parabola, y2 = 4x at the points A & B. The co-ordinates of the point of intersection of the tangents drawn at the points A & B are
a)
b)
c)
d)
|
Yash Patel answered |
ky=[4(x+h)]/2
=> 2ky=2(x+h)
2ky=4x+4h =>4x−2ky+4h=0
4x−7y+10=0
4h=10 => h=5/2
2k=7 => k=7/2
point of intersection of tangent at p and q is (5/2,7/2)
=> 2ky=2(x+h)
2ky=4x+4h =>4x−2ky+4h=0
4x−7y+10=0
4h=10 => h=5/2
2k=7 => k=7/2
point of intersection of tangent at p and q is (5/2,7/2)
The equation of the circle having the lines y2 – 2y + 4x – 2xy = 0 as its normals & passing through the point (2, 1) is- a)x2 + y2 – 2x – 4y + 3 = 0
- b)x2 + y2 – 2x + 4y – 5 = 0
- c)x2 + y2 + 2x + 4y – 13 = 0
- d)None
Correct answer is option 'A'. Can you explain this answer?
The equation of the circle having the lines y2 – 2y + 4x – 2xy = 0 as its normals & passing through the point (2, 1) is
a)
x2 + y2 – 2x – 4y + 3 = 0
b)
x2 + y2 – 2x + 4y – 5 = 0
c)
x2 + y2 + 2x + 4y – 13 = 0
d)
None
|
|
Geetika Shah answered |
The normal line to circle is →y² - 2 y + 4 x -2 xy=0
→ y(y-2) - 2x(y-2)=0
→ (y-2)(y-2x)=0
the two lines are , y=2 and 2 x -y =0
The point of intersection of normals are centre of circle.
→ Put , y=2 in 2 x -y=0, we get
→2 x -2=0
→2 x=2
→ x=1
So, the point of intersection of normals is (1,2) which is the center of circle.
Also, the circle passes through (2,1).
Radius of circle is given by distance formula = [(1-2)² + (2-1)²]½
=(1+1)½ =(2)½
The equation of circle having center (1,2) and radius √2 is
= (x-1)²+(y-2)²=[√2]²
→ (x-1)²+(y-2)²= 2
x²+y² -2x-4y+3 = 0
→ y(y-2) - 2x(y-2)=0
→ (y-2)(y-2x)=0
the two lines are , y=2 and 2 x -y =0
The point of intersection of normals are centre of circle.
→ Put , y=2 in 2 x -y=0, we get
→2 x -2=0
→2 x=2
→ x=1
So, the point of intersection of normals is (1,2) which is the center of circle.
Also, the circle passes through (2,1).
Radius of circle is given by distance formula = [(1-2)² + (2-1)²]½
=(1+1)½ =(2)½
The equation of circle having center (1,2) and radius √2 is
= (x-1)²+(y-2)²=[√2]²
→ (x-1)²+(y-2)²= 2
x²+y² -2x-4y+3 = 0
The equations of the tangents drawn from the point (0, 1) to the circle x2 + y2 - 2x + 4y = 0 are- a)2x - y + 1 = 0, x + 2y - 2 = 0
- b)2x - y - 1 = 0, x + 2y - 2 = 0
- c)2x - y + 1 = 0, x + 2y + 2 = 0
- d)2x - y - 1 = 0, x + 2y + 2 = 0
Correct answer is option 'A'. Can you explain this answer?
The equations of the tangents drawn from the point (0, 1) to the circle x2 + y2 - 2x + 4y = 0 are
a)
2x - y + 1 = 0, x + 2y - 2 = 0
b)
2x - y - 1 = 0, x + 2y - 2 = 0
c)
2x - y + 1 = 0, x + 2y + 2 = 0
d)
2x - y - 1 = 0, x + 2y + 2 = 0
|
|
Geetika Shah answered |
Let equation of tangent with slope =m and point (0,1)
(y−1)=m(x−0)⇒y=mx+1
Intersection point
x2+(mx+1)2−2x+4(mx+1)=0
(1+m2)x2+(−2+6m)x+5=0
For y=mx+1 to be tangent, discriminant =0
(6m−2)2−4×5(1+m2)=0
36m2+4−24m−20m2+20=0
16m2−20m+24=0
⇒ 2m2−3m−2=0
(2m+1)(m−2)=0
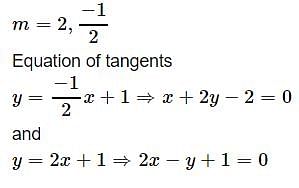
(y−1)=m(x−0)⇒y=mx+1
Intersection point
x2+(mx+1)2−2x+4(mx+1)=0
(1+m2)x2+(−2+6m)x+5=0
For y=mx+1 to be tangent, discriminant =0
(6m−2)2−4×5(1+m2)=0
36m2+4−24m−20m2+20=0
16m2−20m+24=0
⇒ 2m2−3m−2=0
(2m+1)(m−2)=0
such that DAOB (where `O' is the origin) is an equilateral triangle, then the eccentricity e of the hyperbola satisfies
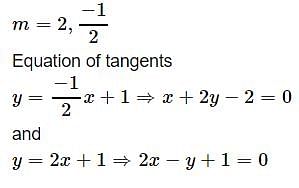
If the eccentricity of the hyperbola x2 – y2 sec2 a = 5 is (√3) times the eccentricity of the ellipse x2 sec2 a + y2 = 25, then a value e of a is- a)π/6
- b)π/4
- c)π/3
- d)π/2
Correct answer is option 'B'. Can you explain this answer?
If the eccentricity of the hyperbola x2 – y2 sec2 a = 5 is (√3) times the eccentricity of the ellipse x2 sec2 a + y2 = 25, then a value e of a is
a)
π/6
b)
π/4
c)
π/3
d)
π/2
|
|
Rishika Shah answered |
Given Information:
The eccentricity of the hyperbola x^2 - y^2 sec^2a = 5 is √3 times the eccentricity of the ellipse x^2 sec^2a + y^2 = 25.
To Find:
The value of 'a' where the eccentricity of the hyperbola is √3 times the eccentricity of the ellipse.
Solution:
Step 1: Find the eccentricity of the hyperbola
For a hyperbola of the form x^2/a^2 - y^2/b^2 = 1, the eccentricity is given by e = √(1 + b^2/a^2).
In this case, the hyperbola is x^2 - y^2 sec^2a = 5.
Comparing, we get a^2 = 5 and b^2 = 1.
So, the eccentricity of the hyperbola is e_hyperbola = √(1 + 1/5) = √(6/5).
Step 2: Find the eccentricity of the ellipse
For an ellipse of the form x^2/a^2 + y^2/b^2 = 1, the eccentricity is given by e = √(1 - b^2/a^2).
In this case, the ellipse is x^2 sec^2a + y^2 = 25.
Comparing, we get a^2 = 25 and b^2 = sec^2a.
So, the eccentricity of the ellipse is e_ellipse = √(1 - sec^2a/25) = √(24/25).
Step 3: Given Condition
It is given that e_hyperbola = √3 * e_ellipse.
Therefore, √(6/5) = √3 * √(24/25).
Solving this equation, we get sec^2a = 8/5.
Step 4: Find the value of 'a'
From sec^2a = 8/5, we get cos^2a = 5/8.
Taking the square root, we get cos a = √(5/8).
Taking the inverse cosine, we get a = π/4.
Therefore, the value of 'a' for the given conditions is π/4. Hence, option 'B' is the correct answer.
The eccentricity of the hyperbola x^2 - y^2 sec^2a = 5 is √3 times the eccentricity of the ellipse x^2 sec^2a + y^2 = 25.
To Find:
The value of 'a' where the eccentricity of the hyperbola is √3 times the eccentricity of the ellipse.
Solution:
Step 1: Find the eccentricity of the hyperbola
For a hyperbola of the form x^2/a^2 - y^2/b^2 = 1, the eccentricity is given by e = √(1 + b^2/a^2).
In this case, the hyperbola is x^2 - y^2 sec^2a = 5.
Comparing, we get a^2 = 5 and b^2 = 1.
So, the eccentricity of the hyperbola is e_hyperbola = √(1 + 1/5) = √(6/5).
Step 2: Find the eccentricity of the ellipse
For an ellipse of the form x^2/a^2 + y^2/b^2 = 1, the eccentricity is given by e = √(1 - b^2/a^2).
In this case, the ellipse is x^2 sec^2a + y^2 = 25.
Comparing, we get a^2 = 25 and b^2 = sec^2a.
So, the eccentricity of the ellipse is e_ellipse = √(1 - sec^2a/25) = √(24/25).
Step 3: Given Condition
It is given that e_hyperbola = √3 * e_ellipse.
Therefore, √(6/5) = √3 * √(24/25).
Solving this equation, we get sec^2a = 8/5.
Step 4: Find the value of 'a'
From sec^2a = 8/5, we get cos^2a = 5/8.
Taking the square root, we get cos a = √(5/8).
Taking the inverse cosine, we get a = π/4.
Therefore, the value of 'a' for the given conditions is π/4. Hence, option 'B' is the correct answer.
The locus of a point such that two tangents drawn from it to the parabola y2 = 4ax are such that the slope of one is double the other is- a) y2 =
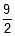ax - b) y2 =
ax - c) y2 = 9ax
- d)x2 = 4ay
Correct answer is option 'A'. Can you explain this answer?
The locus of a point such that two tangents drawn from it to the parabola y2 = 4ax are such that the slope of one is double the other is
a)
y2 = 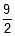ax
axb)
y2 = ax
axc)
y2 = 9ax
d)
x2 = 4ay
|
|
Riya Banerjee answered |
Let the point be (h, k)
Now equation of tangent to the parabola y2 = 4ax whose slope is m is
as it passes through (h, k)]
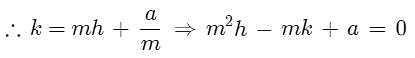
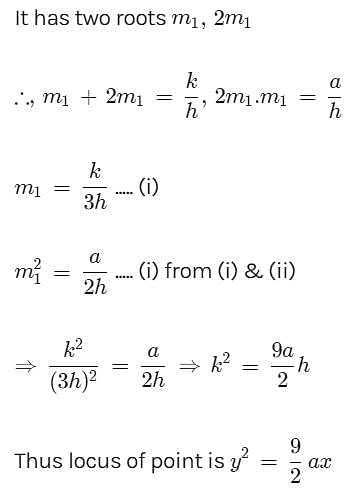
as it passes through (h, k)]
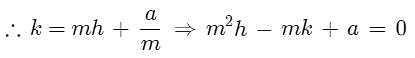
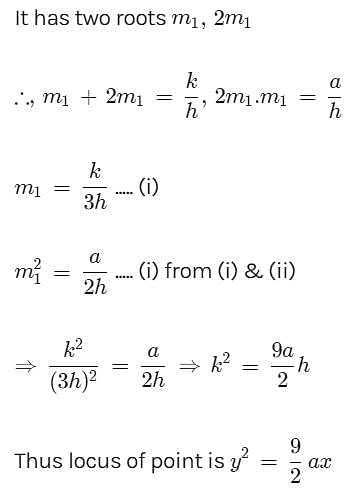
The eccentricity of an ellipse, with its centre at the origin, is 1/2. If one of the directrix is x = 4, then the equation of the ellipse is:- a)
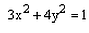
- b)
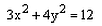
- c)
- d)
Correct answer is option 'B'. Can you explain this answer?
The eccentricity of an ellipse, with its centre at the origin, is 1/2. If one of the directrix is x = 4, then the equation of the ellipse is:
a)
b)
c)
d)
|
|
Naina Sharma answered |
Let the equation of ellipse (x2)/(a2)+(y2)/(b2)=1
Here a > ba > b because the directrix is parallel to y axis.
b2=a2(1−e2)
Given e= 1/2
⇒b2 = (3/4)a2
But a/e=4
⇒a=2
Putting a=2 we get b= (3)1/2
Required ellipse is (x2)/4+(y2)/3=1
⇒3x2+4y2=12
Here a > ba > b because the directrix is parallel to y axis.
b2=a2(1−e2)
Given e= 1/2
⇒b2 = (3/4)a2
But a/e=4
⇒a=2
Putting a=2 we get b= (3)1/2
Required ellipse is (x2)/4+(y2)/3=1
⇒3x2+4y2=12
If the product of the perpendicular distances from any point on the hyperbola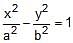 
of eccentricity e= on its asymptotes is equal to 6, then the length of the transverse axis of the hyperbola is- a)3
- b)6
- c)8
- d)12
Correct answer is option 'B'. Can you explain this answer?
If the product of the perpendicular distances from any point on the hyperbola 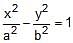of eccentricity e= on its asymptotes is equal to 6, then the length of the transverse axis of the hyperbola is
of eccentricity e= on its asymptotes is equal to 6, then the length of the transverse axis of the hyperbola isa)
3
b)
6
c)
8
d)
12
|
|
Naina Sharma answered |
e2 = (a2 / b2) + 1
3 = (a2 / b2) + 1
a2/b2 = 2
a2 = 2b2
Product of perpendicular distance of any point on hyperbola = (a2b2)/a2 + b2
= [2(b2).b2]/(2b2 + b2)
= [2b2]/3 = 6
= 2b2 = 18
=> b2 = 9
=> b = 3
Length (2b) = 2(3)
= 6
3 = (a2 / b2) + 1
a2/b2 = 2
a2 = 2b2
Product of perpendicular distance of any point on hyperbola = (a2b2)/a2 + b2
= [2(b2).b2]/(2b2 + b2)
= [2b2]/3 = 6
= 2b2 = 18
=> b2 = 9
=> b = 3
Length (2b) = 2(3)
= 6
=1, the length of the major axis is
The foci of the ellipse 25 (x + 1)2 + 9(y + 2)2 = 225 are at:- a)(–2, 1) and (–2, 6)
- b)(–1, 2) and (–1, –6)
- c)(–1, –2) and (–1, –6)
- d)(–1, –2) and (–2, –1)
Correct answer is option 'B'. Can you explain this answer?
The foci of the ellipse 25 (x + 1)2 + 9(y + 2)2 = 225 are at:
a)
(–2, 1) and (–2, 6)
b)
(–1, 2) and (–1, –6)
c)
(–1, –2) and (–1, –6)
d)
(–1, –2) and (–2, –1)
|
|
Poonam Reddy answered |
Here equation of ellipse is 25(x + 1)2 + 9(y + 2)2 = 225
0r (x + 1)2/9 + (y + 2)2/25 = 1
Centre of the ellipse is (–1,–2)
a2 = 9, b2 = 25
a = 3, b = 5
e = (1-a2/b2)1/2
e = (1-9/25)1/2
e = +-4/5
be = +-4
Foci : (-1,-6)(-1,2)
0r (x + 1)2/9 + (y + 2)2/25 = 1
Centre of the ellipse is (–1,–2)
a2 = 9, b2 = 25
a = 3, b = 5
e = (1-a2/b2)1/2
e = (1-9/25)1/2
e = +-4/5
be = +-4
Foci : (-1,-6)(-1,2)
If (x2−a)2+(y−b)2 = c2 represents a circle, then
- a)b = 0
- b)a = b = 0
- c)a = 0
- d)c ≠ 0
Correct answer is option 'D'. Can you explain this answer?
If (x2−a)2+(y−b)2 = c2 represents a circle, then
a)
b = 0
b)
a = b = 0
c)
a = 0
d)
c ≠ 0
|
Swati Reddy answered |
I am sorry, but your question is incomplete. Please provide the missing information so I can assist you better.
Locus of the point of intersection of the perpendicular tangents of the curve y2 + 4y – 6x – 2 = 0 is- a) 2x – 1 = 0
- b)2x + 3 = 0
- c)2y + 3 = 0
- d)2x + 5 = 0
Correct answer is option 'C'. Can you explain this answer?
Locus of the point of intersection of the perpendicular tangents of the curve y2 + 4y – 6x – 2 = 0 is
a)
2x – 1 = 0
b)
2x + 3 = 0
c)
2y + 3 = 0
d)
2x + 5 = 0
|
|
Geetika Shah answered |
Given parabola is, y2+4y−6x−2=0
⇒ y2+4y+4=6x+6=6(x+1)
⇒ (y+2)2 = 6(x+1)
shifting origin to (−1,−2)
Y2 = 4aX where a = 3/2
We know locus of point of intersection of perpendicular tangent is directrix of the parabola itself
Hence required locus is X=−a ⇒ x+1=−3/2
⇒ 2x+5=0
⇒ y2+4y+4=6x+6=6(x+1)
⇒ (y+2)2 = 6(x+1)
shifting origin to (−1,−2)
Y2 = 4aX where a = 3/2
We know locus of point of intersection of perpendicular tangent is directrix of the parabola itself
Hence required locus is X=−a ⇒ x+1=−3/2
⇒ 2x+5=0
Which one of the following equations represents parametrically, parabolic profile ?- a)x = 3 cost ; y = 4 sint
- b) x2 – 2 = – cost ; y = 4 cos2
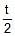
- c)
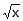= tan t ; 
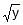= sec t - d) x =
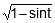; y = sin
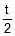+ cos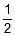
Correct answer is option 'B'. Can you explain this answer?
Which one of the following equations represents parametrically, parabolic profile ?
a)
x = 3 cost ; y = 4 sint
b)
x2 – 2 = – cost ; y = 4 cos2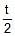
c)
= tan t ; = sec td)
x = 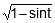; y = sin 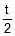+ cos
; y = sin + cos|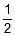
|
Hansa Sharma answered |
x2 − 2 = −2cost
⇒ x2 = 2 − 2cost
⇒x2 = 2(1−cost)
⇒x2 = 2(1−(1−2sin2 t/2))
⇒x2 = 4sin2 t/2
We have y = 4cos2 t/2
⇒cos2 t/2= y/4
We know the identity, sin2 t/2 + cos2 t/2 = 1
⇒ x2/4 + y/4 = 1
⇒ x2 = 4−y represents a parabolic profile.
⇒ x2 = 2 − 2cost
⇒x2 = 2(1−cost)
⇒x2 = 2(1−(1−2sin2 t/2))
⇒x2 = 4sin2 t/2
We have y = 4cos2 t/2
⇒cos2 t/2= y/4
We know the identity, sin2 t/2 + cos2 t/2 = 1
⇒ x2/4 + y/4 = 1
⇒ x2 = 4−y represents a parabolic profile.
The equation of the transverse and conjugate axes of a hyperbola are respectively x + 2y – 3 = 0, 2x – y + 4 = 0 and their respective lengths are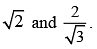 
The equation of the hyperbola is- a)
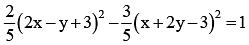
- b)
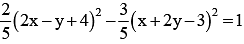
- c)
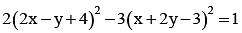
- d)2(x + 2y -3)2 -3 (2x - y + 4)2 = 1
Correct answer is option 'A'. Can you explain this answer?
The equation of the transverse and conjugate axes of a hyperbola are respectively x + 2y – 3 = 0, 2x – y + 4 = 0 and their respective lengths are 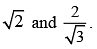The equation of the hyperbola is
The equation of the hyperbola isa)
b)
c)
d)
2(x + 2y -3)2 -3 (2x - y + 4)2 = 1
|
|
Vikas Kapoor answered |
Equation of the hyperbola is
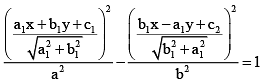
Where a1x + b1y + c1 = 0, b1x - a1y + c2 = 0 are conjugate and transverse axes respectively and a, b are lengths of semitransverse and semiconjugate axes respectively.
Where a1x + b1y + c1 = 0, b1x - a1y + c2 = 0 are conjugate and transverse axes respectively and a, b are lengths of semitransverse and semiconjugate axes respectively.
The greatest distance of the point P(10, 7) from the circle x2 + y2 – 4x – 2y – 20 = 0 is- a)5
- b)15
- c)10
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
The greatest distance of the point P(10, 7) from the circle x2 + y2 – 4x – 2y – 20 = 0 is
a)
5
b)
15
c)
10
d)
None of these
|
|
Sankar Mehta answered |
The equation of the circle is x^2 + y^2 = r^2, where r is the radius of the circle. We need to find the value of r first.
The circle passes through the origin (0,0), since x^2 + y^2 = 0^2 when x = 0 and y = 0. Therefore, the distance from the center of the circle to the origin is equal to the radius.
The center of the circle is at (0,0), so the distance from the center to the point P(10,7) is:
d = sqrt((10-0)^2 + (7-0)^2) = sqrt(149)
Therefore, the radius of the circle is r = sqrt(149).
The greatest distance from the point P(10,7) to the circle is the distance from the point to the edge of the circle along a line that passes through the center of the circle. This is equal to the difference between the distance from the center to the point and the radius of the circle.
The distance from the center of the circle to the point P(10,7) is d = sqrt((10-0)^2 + (7-0)^2) = sqrt(149).
Therefore, the greatest distance of the point P(10,7) from the circle is:
d - r = sqrt(149) - sqrt(149) = 0.
Therefore, the greatest distance is 0, which means that the point P(10,7) is on the circle.
The circle passes through the origin (0,0), since x^2 + y^2 = 0^2 when x = 0 and y = 0. Therefore, the distance from the center of the circle to the origin is equal to the radius.
The center of the circle is at (0,0), so the distance from the center to the point P(10,7) is:
d = sqrt((10-0)^2 + (7-0)^2) = sqrt(149)
Therefore, the radius of the circle is r = sqrt(149).
The greatest distance from the point P(10,7) to the circle is the distance from the point to the edge of the circle along a line that passes through the center of the circle. This is equal to the difference between the distance from the center to the point and the radius of the circle.
The distance from the center of the circle to the point P(10,7) is d = sqrt((10-0)^2 + (7-0)^2) = sqrt(149).
Therefore, the greatest distance of the point P(10,7) from the circle is:
d - r = sqrt(149) - sqrt(149) = 0.
Therefore, the greatest distance is 0, which means that the point P(10,7) is on the circle.
Chapter doubts & questions for Conic sections - Mathematics for Year 12 2024 is part of Year 12 exam preparation. The chapters have been prepared according to the Year 12 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Year 12 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Conic sections - Mathematics for Year 12 in English & Hindi are available as part of Year 12 exam.
Download more important topics, notes, lectures and mock test series for Year 12 Exam by signing up for free.
Mathematics for Year 12
154 videos|194 docs|125 tests
|
Signup to see your scores go up within 7 days!
Study with 1000+ FREE Docs, Videos & Tests
10M+ students study on EduRev
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup