All Exams >
GMAT >
Quantitative for GMAT >
All Questions
All questions of Probability & Statistics for GMAT Exam
A group of 30 people includes men, women and children. If one person is to be chosen at random from the group, is the probability that a man is chosen greater than the probability that a woman is chosen?(1) The probability that a man is chosen is 50% greater than the probability that a child is chosen.(2) The probability that either a woman or a child is chosen is greater than the probability that a man is chosen- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'E'. Can you explain this answer?
A group of 30 people includes men, women and children. If one person is to be chosen at random from the group, is the probability that a man is chosen greater than the probability that a woman is chosen?
(1) The probability that a man is chosen is 50% greater than the probability that a child is chosen.
(2) The probability that either a woman or a child is chosen is greater than the probability that a man is chosen
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
Anaya Patel answered |
Steps 1 & 2: Understand Question and Draw Inferences
Given:
- Let number of Men Women, Children be M, W, C respectively.
- M + W + C = 30
- Since M, W and C denote the number of people in the group, they must be positive integers
To find: Is P(Choosing a man) > P(Choosing a woman)?
Step 3: Analyze Statement 1 independently
- The probability that a man is chosen is 50% greater than the probability that a child is chosen.
- One is tempted to conclude that since this is a linear equation with two unknowns, we’ll not be able to find unique values of M and W, and hence, will not be able to answer the question. However, we should not be so fast in our judgment because we are given a constraint here on the values of M and W:
- M and W can only be positive integers
- Let’s evaluate if this constraint, when combined with the above equation, leads us to unique values of M and W or not:
- We can rewrite the above equation as:
- Since W must be an integer, M must be a multiple of 3
- Thus M must be a positive multiple of 3 and must be less than 16
-
Thus, we see that Statement 1 alone is not sufficient to arrive at a unique answerStep 4: Analyze Statement 2 independently - The probability that either a woman or a child is chosen is greater than the probability that a man is chosen
- P(Choosing a child) =
- P(Choosing a child) =
- P(Choosing a Woman or a child) = P(Choosing a Woman) + P(Choosing a child)
- Therefore, 30–M>M
- (Using M + W + C = 30)
- 30 > 2M
- So, M < 15
- If W = 2, M = 1 and C = 27, this condition is satisfied and the answer to the Question is NO
- If W =8, M = 12 and C = 10, this condition is satisfied and the answer to the Question is YES.
- So, Statement 2 is not sufficient to find a unique answer to the question.Step 5: Analyze Both Statements Together (if needed)
- From Statement 1:
- From Statement 2: M < 15
- All the values of M in the table satisfy this inequality
- Therefore, even after combining both the statements, we don’t’ know if the answer to the question is Yes or No.Answer: Option E
A box contains orange, green and blue balls. If one ball is chosen at random from the box, what is the probability that the chosen ball is orange?(1) The probability that the chosen ball is blue is one-fourth of the probability that the chosen ball is not blue(2) If there were 15 fewer orange balls in the box, the probability that the chosen ball is orange would have been equal to the probability that the chosen ball is blue- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'E'. Can you explain this answer?
A box contains orange, green and blue balls. If one ball is chosen at random from the box, what is the probability that the chosen ball is orange?
(1) The probability that the chosen ball is blue is one-fourth of the probability that the chosen ball is not blue
(2) If there were 15 fewer orange balls in the box, the probability that the chosen ball is orange would have been equal to the probability that the chosen ball is blue
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
Lavanya Menon answered |
Given:
- Let the number of orange, green and blue balls be R, G and B respectively.
To find: P(R)
Step 3: Analyze Statement 1 independently
- The probability that the chosen ball is blue is one-fourth of the probability that the chosen ball is not blue
But the expression for the probability that the chosen ball is blue =BR+G+B=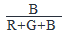 
- We do not know the exact values of R and G. Nor do we know the value of the ratio R:G
- So, we cannot find a unique value of P(R ) from the above equation.
Statement 1 is not sufficient to find a unique answer to the question
Step 4: Analyze Statement 2 independently
- If there were 15 fewer orange balls in the box, the probability that the chosen ball is orange would have been equal to the probability that the chosen ball is blue
- Number of orange balls = R – 15
- Number of blue balls = B
- Number of green balls = G
- So, The total number of balls in this case = G + B + (R – 15)
- Since we do not know the unique values of R and G, we cannot find the value of P(R)
Thus, Statement 2 alone is not sufficient to answer the question
Step 5: Analyze Both Statements Together (if needed)
- So, total number of balls,
- So,
- Since we don’t know the value of R, we cannot find this probability.
- Therefore, the 2 statements together are also not sufficient to answer the question.Answer: Option E
If scores of 10 students in a class are arranged in the table (shown below), then what is the Range of their scores?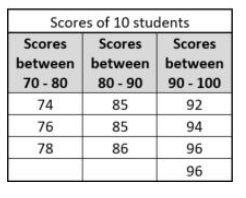 
- a)16
- b)18
- c)20
- d)22
- e)24
Correct answer is option 'D'. Can you explain this answer?
If scores of 10 students in a class are arranged in the table (shown below), then what is the Range of their scores?
a)
16
b)
18
c)
20
d)
22
e)
24
|
|
Anaya Patel answered |
The difference between the highest and lowest observations in a given data is called its Range.
Score of 10 students in ascending order = 74, 76, 78, 85, 85, 86, 92, 94, 96, 96
Then the difference between the highest and lowest value will be 96 - 74
Range = 22
Two distinct fair dice are rolled together. If a fair coin and a biased coin are also tossed together, what is the probability of getting 1 head and 1 tail on the coins and the sum of the two dice greater than 6? Assume that the probability of getting a head on the biased coin is 0.75.- a)7/36
- b)5/24
- c)7/24
- d)5/9
- e)1/2
Correct answer is option 'C'. Can you explain this answer?
Two distinct fair dice are rolled together. If a fair coin and a biased coin are also tossed together, what is the probability of getting 1 head and 1 tail on the coins and the sum of the two dice greater than 6? Assume that the probability of getting a head on the biased coin is 0.75.
a)
7/36
b)
5/24
c)
7/24
d)
5/9
e)
1/2
|
|
Aditya Kumar answered |
Given
- Two distinct dice are rolled together
- Fair coin is tossed
- P(head) = P(tail) = 0.5
- Biased coin is tossed
To Find: Probability of getting 1 head and 1 tail and the sum of the dice > 6
Approach
- Event-1: Probability of getting 1 head and 1 tail
- Event-2: Probability of getting the sum of two dice > 6
- P(Event-1 AND Event-2) = P(Event-1) * P(Event-2)
- Event-1: Getting 1 head and 1 tail on tossing of coins
- Following cases are possible:
- Case-I: Getting a head on the fair coin and a tail on the biased coin OR
- Case-II: Getting a tail on the fair coin and a head on the biased coin
- P(Event-1) = P(case-I) + P(case-II)
- As we know the probability of getting a head and a tail on both the coins, we can calculate the probability of getting a head and a tail on tossing the 2 coins
- Following cases are possible:
- Event-2: Getting the sum of dice > 6
- Event-2: Getting the sum of dice > 6, i.e. {7, 8, 9, 10, 11 or 12}
- Non-Event-2: Getting the sum of dice ≤ 6, i.e. {2, 3, 4, 5 or 6}
- As the non-event has lesser number of cases to calculate, we will solve this with the non-event method
- So, P(Non-Event-2) = P(getting a sum of 2) + P(getting a sum of 3) +……….P(getting a sum of 6)
- So, we need to find the number of ways of getting a sum of 2, 3,…..6 and then divide it by the number of possible ways of rolling the two dices.
- P(Event-2) = 1- P(Non-Event-2
The average (arithmetic mean) of the prime numbers that lie between 10 and 20 is how much greater than the average of the
prime numbers that lie between 1 and 10?- a)10.25
- b)10.75
- c)11
- d)11.25
- e)11.75
Correct answer is option 'B'. Can you explain this answer?
The average (arithmetic mean) of the prime numbers that lie between 10 and 20 is how much greater than the average of the
prime numbers that lie between 1 and 10?
prime numbers that lie between 1 and 10?
a)
10.25
b)
10.75
c)
11
d)
11.25
e)
11.75
|
|
Aditya Kumar answered |
Given:
2 sets of Prime Numbers – let’s call them Sets A and B:
- Set A = {2, 3, 5, 7}
- Set B = {11, 13, 17, 19}
To find: Difference between Average(Set B) and Average (Set A)
- That is, Average(Set B) – Average (Set A)
Approach:
- In order to find the answer, we need to know the values of Average(Set A), Average(Set B)
- Since we know all the elements in each of Set A and B, we will be easily able to find the required averages.
Working out:
Correct Answer – Option B
Alex participates in a shooting competition and makes n attempts to shoot a target. Is the probability that he will shoot the target in all the n attempts that he makes, greater than 50%? - Alex has a 80% chance of shooting the target in every attempt that he makes.
- He makes 7 attempts in total.
- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'C'. Can you explain this answer?
Alex participates in a shooting competition and makes n attempts to shoot a target. Is the probability that he will shoot the target in all the n attempts that he makes, greater than 50%?
- Alex has a 80% chance of shooting the target in every attempt that he makes.
- He makes 7 attempts in total.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.
|
EduRev GMAT answered |
This is a DS question on the concept of probability. So, we will apply the A-B-C approach that we have learnt for Probability questions within the 5-step framework that we universally apply for all DS questions.
Steps 1&2: Understand the question and draw inferences
We know that Alex makes n attempts to shoot the target.
We need to determine the probability that he shoots the target in each of the n attempts.
Let us follow the A-B-C approach to answer this question.
Step A: Write Probability Event Equation
In order to do so, we should list all the events.
Event 1: Alex shoots the target in 1st attempt
Event 2: Alex shoots the target in 2nd attempt, and so on. . .
Event n: Alex shoots the target in nth attempt
Now, we should determine whether ‘AND’ or ‘OR’ applies.
The question statement asks about the probability of Alex shooting the target in everyattempt. So, he needs to shoot the target in the 1st attempt AND in the 2nd attempt and so on. . .
So, the Probability Event Equation will be:
P(Alexshootingthetargetineveryattempt)=P(Event1)×P(Event2)×...×P(Eventn)
Step B: Determine Probabilities of individual events
From the question statement, we do not know:
i) What is the probability of his shooting the target in every attempt
ii) Whether the probability of his shooting the target is equal for every attempt or different
So, let us assume that:
The probability of his shooting the target the first attempt = P1
The probability of his shooting the target in the second attempt = P2 . . .
The probability of his shooting the target in the nth attempt = Pn
Step C: Plug values of Individual Event Probabilities in the Event Equation
Thus, the Event Equation becomes:
P(Alexshootingthetargetineveryattempt)=P1×P2×...×Pn
.......Equation 1
The question asks us whether P(Alex shooting the target in every attempt) is greater than 0.50
In order to answer this question, we need to know the values of P1, P2 . . . Pn
Step 3: Analyze Statement 1 independently
Alex has 80% chance of hitting the target in every attempt that he makes
From this statement, we get:
P1 = P2 = . . . Pn = 0.80
So, Equation 1 becomes:
P(Alex shooting the target in each attempt) = 0.8× 0.8× 0.8...n times
P(Alexshootingthetargetineachattempt)=(0.8)n
Since we do not know the value of n, we will not be able to determine if
P(Alex shooting the target in each attempt ) >0.5
Thus, Statement 1 alone is not sufficient to answer the question.
Step 4: Analyze Statement 2 independently
He makes 7 attempts in total
From this statement, we get n = 7
Thus, from Equation 1, we get:
P(Alex shooting the target in each attempt) =P1×P2×...×P7
However, this statement gives us no clue about the values of P1, P2 . . . P7
Thus, Statement 2 alone is clearly not sufficient to answer the question.
Step 5: Analyze both statements together (if needed)
From Statement 1,
P(Alex shooting the target in each attempt) =(0.8)n
From Statement 2,
n = 7
By combining both statements, we get:
P(Alex shooting the target in each attempt) =(0.8)7
From this equation, we will be able to determine the exact numerical value of the probability that Alex shoots the target in every attempt. Therefore, we will also be able to determine if this value is greater than 0.50 or not.
Thus, both statements together are sufficient to answer the question.
Answer: Option (C)
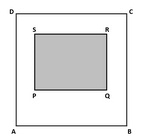In the figure above, rectangle PQRS is a shaded region inside the square ABCD. What is the probability that a point chosen at random from the square ABCD will lie inside the shaded rectangle PQRS?(1) The length of a diagonal of rectangle PQRS is 55% the length of a diagonal of square ABCD(2) The length of side PQ is 20% greater than the length of side QR- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'C'. Can you explain this answer?
In the figure above, rectangle PQRS is a shaded region inside the square ABCD. What is the probability that a point chosen at random from the square ABCD will lie inside the shaded rectangle PQRS?
(1) The length of a diagonal of rectangle PQRS is 55% the length of a diagonal of square ABCD
(2) The length of side PQ is 20% greater than the length of side QR
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
|
Aditya Kumar answered |
Steps 1 & 2: Understand Question and Draw Inferences
Given: The figure that shows rectangle PQRS inside square ABCD
To find: Probability that a randomly chosen point from the square lies inside the rectangle PQRS
Step 3: Analyze Statement 1 independently
Statement 1 says that ‘The length of a diagonal of rectangle PQRS is 55% the length of a diagonal of square ABCD’
The above equation has 2 unknowns:
- So, we cannot find a unique value of the required ratios from this single equation
- Therefore, Statement 1 is not sufficient.
Step 4: Analyze Statement 2 independently
Statement 2 says that ‘The length of side PQ is 20% greater than the length of side QR’
However, in order to answer the question, we need to know the value of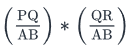 
- Since Statement 2 doesn’t provide us with these ratios, it is not sufficient.
Step 5: Analyze Both Statements Together (if needed)
- Rejecting the negative root since the ratio of two lengths cannot be negative
- Thus, by combining the 2 statements, we get a unique value of the ratio QR/AB
- By substituting the equation from Statement 2, we can also get a unique value of the ratio PQ/AB
- So, we will be able to find the value of
- Thus, the 2 statements together are sufficient to answer the question
Frequency Distribution of Integers in Set X and Set Y 
X and Y are two sets that contain integers as shown the table above. What is the probability that the product of a randomly chosen integer from Set X and a randomly chosen integer from Set Y will be even?- a)1/15
- b)13/354
- c)1/5
- d)1/2
- e)4/5
Correct answer is option 'D'. Can you explain this answer?
Frequency Distribution of Integers in Set X and Set Y
X and Y are two sets that contain integers as shown the table above. What is the probability that the product of a randomly chosen integer from Set X and a randomly chosen integer from Set Y will be even?
a)
1/15
b)
13/354
c)
1/5
d)
1/2
e)
4/5
|
|
Aditya Kumar answered |
Given:
- Sets X and Y contain integers as shown in the table.
- 1 integer is chosen from X (the integer chosen from Set X will be referred to as IX from now on) and one from Y (IY)
To find: The probability that IX*IY is Even
Approach:
- P(IX*IY is Even) = 1 – P(IX*IY is Odd)
- The reason why we are taking the Non-Event Approach here is that there are 3 ways in which the product of 2 integers can be Even ( i. Both integers are even ii. Only IX is even and iii. Only IY is even). However, there is only one way in which IX*IY is odd (when both the integers are odd). So, it’s easier and quicker to solve the question using the Non-Event Approach.
- Since the product IX*IY is odd when IX and IY are odd, we can write:
- P(IX*IY is Odd) = P(IX is odd)*P(IY is odd)
- So, we need to find P(IX is odd) and P(IY is odd)
Working Out:
- Finding P(IX is odd)
The total number of integers in Set X is 30
- So, the total number of ways in which one integer can be selected from Set X =
- The odd integers in Set X (3, 5, 7) are highlighted in the table. 3 occurs 4 times in Set X, 5 occurs 6 times and 7 occurs 8 times
- So, the total number of odd integers in Set X = 4 + 6 + 8 = 18
- So, the number of ways in which one ODD integer can be selected from Set X=
- Therefore, P(IX is odd) =
- Finding P(IY is odd)
- The total number of integers in Set Y is 12
- So, the total number of ways in which one integer can be selected from Set
- All the integers in Set Y are odd (highlighted in the table) except the two occurrences of 24.
- So, the total number of odd integers in Set Y = 12 – 2 = 10
- So, the number of ways in which one ODD integer can be selected from Set Y =
- Therefore, P(IY is odd) =
Finding the Required Probability
Looking at the answer choices, we see that the correct answer is Option DIf scores of 10 students in a class are arranged in the table (shown below), then what is the Median of their scores?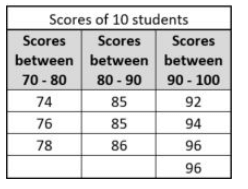
- a)84
- b)84.5
- c)85
- d)85.5
- e)86
Correct answer is option 'D'. Can you explain this answer?
If scores of 10 students in a class are arranged in the table (shown below), then what is the Median of their scores?
a)
84
b)
84.5
c)
85
d)
85.5
e)
86
|
Bank Exams India answered |
Score of 10 students in ascending order = 74, 76, 78, 85, 85, 86, 92, 94, 96, 96
Since number of observations is even, the median is given by finding the average or mean of the two middle most observations.
So, median = (85 + 86)/2
Median = 85.5
If x is an integer such that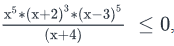 
what is the probability that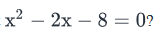 
- a)1/7
- b)1/6
- c)1/4
- d)2/7
- e)1/3
Correct answer is option 'B'. Can you explain this answer?
If x is an integer such that 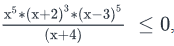what is the probability that
what is the probability that a)
1/7
b)
1/6
c)
1/4
d)
2/7
e)
1/3
|
Meera Rana answered |
Given
To Find: The probability that x2 - 2x -8 =0 ?
We need to find the probability that x = -2, or 4
- We need to find the probability that x = -2, or 4
Approach
- Possible number of ways for which
2. Possible number of values that x can takeà For finding the values that x can take, we need to solve the inequality 
3. Probability of
4. For solving the inequality, we will use the wavy line method
Woking Out
1. 
- Now, we can see that the inequality is satisfied at {-3, -2, 0, 1, 2, 3}, i.e. a total of 6 values….(1)
- Please note that we have not considered x = -4 as one of the solution points, because for x = -4, the denominator becomes 0
- As we do not have x = 4 as one of the solutions, x2 - 2x -8 =0 only when x = -2
- So, the probability of (x = -2) = 1/6
- So, out of the possible 6 values of x, for only one value of x = -2.
When positive integer y is added to each of the first n non-negative integers, which of the following statements is true?
I. If the median of the resulting numbers is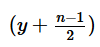 
then n is oddII. The arithmetic mean of the resulting numbers is equal to the median of the resulting numbers
III. The arithmetic mean of the resulting numbers is y units greater than the arithmetic mean of the first n positive integers.- a)I only
- b)II only
- c)III only
- d)I, II and III
- e)None of the above
Correct answer is option 'B'. Can you explain this answer?
When positive integer y is added to each of the first n non-negative integers, which of the following statements is true?
I. If the median of the resulting numbers is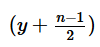 then n is odd
I. If the median of the resulting numbers is
then n is oddII. The arithmetic mean of the resulting numbers is equal to the median of the resulting numbers
III. The arithmetic mean of the resulting numbers is y units greater than the arithmetic mean of the first n positive integers.
III. The arithmetic mean of the resulting numbers is y units greater than the arithmetic mean of the first n positive integers.
a)
I only
b)
II only
c)
III only
d)
I, II and III
e)
None of the above
|
Naroj Boda answered |
Given:
- The list of first n non-negative integers: {0, 1, 2, 3, . . . , n – 1}
- Positive integer y is added to each integer in this list: {0 + y, 1 + y, 2 + y, . . . n – 1 + y}
- = {y, y + 1, y + 2, . . . , y + n – 1}
To Find: Which of the 3 statements is/are true?
Approach:
- Since these 3 statements deal with:
- Mean of the first n positive integers
- Mean of the resulting numbers
- And, Median of the resulting numbers,
We will first find the expressions for these 3 quantities.
2. Then, we’ll evaluate the 3 statements one by one to determine which is/are true for all values of y and n
Working out:
- Finding the expressions for the 3 quantities featured in Statements I – III
- Finding Mean of the first n positive integers
- Sum of first n positive integers =
- So, the mean of the first n positive integers =
- (n+2/2)
- Sum of first n positive integers =
- Finding Mean of the first n positive integers
- Finding Mean of the Resulting Numbers
- The resulting numbers are: {y, y + 1, y + 2, . . . , y + n – 1}
- These numbers form an increasing arithmetic sequence of n terms.
- First term of the sequence = y
- Last term of the sequence = y + n -1
- So, the sum of these numbers =
- These numbers form an increasing arithmetic sequence of n terms.
- The resulting numbers are: {y, y + 1, y + 2, . . . , y + n – 1}
- Finding Median of the Resulting Numbers
- The resulting numbers are: {y, y + 1, y + 2, . . . , y + n – 1}
- The total number of elements in this set is (y + n – 1) – y + 1 = n
- These numbers form an increasing arithmetic sequence of n terms.
- Now, in an ordered list that has:
- An even number of elements (say 4 elements), the median of the list is equal to the average of the middle 2 elements of the list
- An odd number of elements (Say 5 elements), the median of the list is equal to the middle element in the list
- Case 1: If n is odd,
- Then, Median = the middle element in the list of resulting numbers
- The first term in the list is y + 0 and the last term is y +(n – 1)
- So, the Median =
- (Note: If the above expression for the Median is not intuitive to you, you can arrive at it by taking a few easy values of n. For example:
- If n = 3, the list is {y, y + 1, y + 2}. So, the median = y + 1
- If n = 5, the list is {y, y + 1. y + 2, y + 3, y + 4}. So, the median = y + 2
- Similarly, if n = 7, the list goes from y to y + 6 and the median = y + 3
- From these examples, the pattern for how the value of Median changes with n becomes easy to see)
- Case 2: If n is even,
- This means, the median of the list is equal to the
- This means, the median of the list is equal to the
- Evaluating Statement I
- If the median of the resulting numbers is
then n is odd - In our calculation of the Median of the Resulting Numbers, observe that the median is always equal to , whether n is even or odd.
- Therefore, Statement I is not correct
- If the median of the resulting numbers is
- Evaluating Statement II
- The arithmetic mean of the resulting numbers is equal to the median of the resulting numbers
- From our calculations of the Mean and Median of the Resulting Numbers, we see that:
- Mean of the Resulting numbers =
- Median =
- Mean of the Resulting numbers =
- From our calculations of the Mean and Median of the Resulting Numbers, we see that:
- So, Statement II is indeed true.
- The arithmetic mean of the resulting numbers is equal to the median of the resulting numbers
- Evaluating Statement III
- The arithmetic mean of the resulting numbers is y units greater than the arithmetic mean of the first n positive integers.
- From our calculations above, we see that:
- Mean of the Resulting numbers =
- Mean of the first n positive integers
- Mean of the Resulting numbers =
- Note that
is not equal to . Therefore, it is wrong to say that Mean of the Resulting Numbers is y units greater than the Mean of the first n positive integers. - So, Statement III is not true.
- Getting to the answer
- Of the 3 statements, we see that only Statement II is true.
Looking at the answer choices, we see that the correct answer is Option B
Find the chance of throwing at least one ace in a simple throw with two dice- a)1/12
- b)1/3
- c)1/4
- d)11/36
Correct answer is option 'D'. Can you explain this answer?
Find the chance of throwing at least one ace in a simple throw with two dice
a)
1/12
b)
1/3
c)
1/4
d)
11/36
|
Ravi Singh answered |
The possible number of cases is 6×6, or 36.
An ace on one die may be associated with any of the 6 numbers on the other die, and the remaining 5 numbers on the first die may each be associated with the ace on the second die; thus the number of favourable cases is 11.
Therefore the required chance is 11/36
An ace on one die may be associated with any of the 6 numbers on the other die, and the remaining 5 numbers on the first die may each be associated with the ace on the second die; thus the number of favourable cases is 11.
Therefore the required chance is 11/36
From a set of consecutive numbers from 1 to 20 (both inclusive) a number is selected. What is the probability that the selected number is divisible by 5?- a)1/20
- b)1/10
- c)1/5
- d)1/4
- e)1/2
Correct answer is option 'C'. Can you explain this answer?
From a set of consecutive numbers from 1 to 20 (both inclusive) a number is selected. What is the probability that the selected number is divisible by 5?
a)
1/20
b)
1/10
c)
1/5
d)
1/4
e)
1/2
|
Talent Skill Learning answered |
Step I: Define the Event
We are given a set of 20 numbers. A single number is selected from this set. The event will be the selection of a number that is divisible by 5
Step II: Find n, the number of ways in which all outcomes can occur
As we know there are 20 numbers in the set. Any of these numbers may be selected.
Thus, n = 20C1 = 20
Step III: Find x, the number of ways in which the event can occur
To find x, we should list the numbers between 1 and 20 that are divisible by 5. These numbers are:
5, 10, 15 and 20.
Thus, there are 4 numbers between 1 and 20 that are divisible by 5.
The event will occur if any of these 4 numbers is selected.
Thus, x = 4C1 = 4
Step IV: Probability = x/n
P = x/n = 4/20 = 1/5
So, the probability of the selected number being divisible by 5 is 1/5.
Answer: Option (C)
From January to October, the revenue of a textile manufacturing plant averaged 20,000 USD per month. What average monthly revenue in USD was required in November and December, if the plant had a goal to achieve 330,000 USD in revenue by the end of the calendar year? - a)65000
- b)75000
- c)80000
- d)100000
- e)110000
Correct answer is option 'A'. Can you explain this answer?
From January to October, the revenue of a textile manufacturing plant averaged 20,000 USD per month. What average monthly revenue in USD was required in November and December, if the plant had a goal to achieve 330,000 USD in revenue by the end of the calendar year?
a)
65000
b)
75000
c)
80000
d)
100000
e)
110000
|
Sravya Joshi answered |
Step 1: Question statement and Inferences
We are given that the average revenue for a textile manufacturing plant was 20,000 USD per month from January till October. The plant wanted to achieve a total revenue of 330,000 USD by the end of the year.
We have to find the average revenue that the plant must achieve in November and December to meet its total targeted revenue.
Let’s say the monthly revenues for the plant are M1, M2, M3 ….. M12.
Now, we don’t know the individual values of the monthly revenues. But we do know that the average monthly revenue for the first ten months is USD 20,000. Thus,
Hence,
M1 + M2 + M3 …. + M10 = 200,000 ………… (1)
The targeted revenue for the year is USD 330,000. Thus,
M1 + M2 + M3 …. + M11 + M12 = 330,000 ………… (2)
Step 2: Finding required values
The question wants us to find the average monthly revenue for November and December. Let’s say the average monthly revenue for these two months is X. Thus,
That is, M11 + M12 = 2X ………… (3)
Substituting values from Equations 1 and 3 in Equation 2:
200,000 + 2X = 330,000
2X = 130,000
X = 65,000
So, the average monthly revenue for the months of November and December is 65,000 USD.
Answer: Option (A)
In a classroom, 40% of the boys had read a particular book. What was the probability that a student who was randomly selected from the classroom was a girl who had read the book?(1) Three-eighths of all students in the classroom had read the book(2) 20 girls in the classroom had not read the book- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'E'. Can you explain this answer?
In a classroom, 40% of the boys had read a particular book. What was the probability that a student who was randomly selected from the classroom was a girl who had read the book?
(1) Three-eighths of all students in the classroom had read the book
(2) 20 girls in the classroom had not read the book
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
|
|
Disha Mehta answered |
teps 1 & 2: Understand Question and Draw Inferences
Given:
- We are given information about the students in the classroom based on 2 attributes:
- Gender – Girls, Boys
- Book – Read, Not Read
- Accordingly, we can draw the following table to represent the information given in this question:
- Let the total number of Boys in the class be B and the total number of girls be G
- As given: 40% of the boys read. So, their number is equal to 0.4B
- Therefore, the number of boys who do not read = B – 0.4B = 0.6B
- (Note: In this solution, the given information will be displayed in black font color in the table, while the inferred information will be displayed in blue font color)
To find: P(Choosing a girl has read the book)
- Let the number of girls who have read the book be GR
- So, Required Probability =
Step 3: Analyze Statement 1 independently
Statement 1 says that ‘Three-eighths of all students in the classroom had read the book’
Therefore,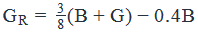 
- This equation will give us an expression for GR in terms of B and G
- So, we will get an expression for the Required Probability in terms of B and G. However, since we do not know the values of B and G (or the ratio B/G), we will not be able to find the value of the Required Probability
- Therefore, Statement 1 alone is not sufficient.
Step 4: Analyze Statement 2 independently
Statement 2 says that ‘20 girls in the classroom had not read the book’
- Therefore, GR = G – 20
- (And Total Students who Read = 0.4B + G – 20)
- So, Required Probability =
- However, since we do not know the values of G and B, we cannot find the value of the Required Probability
- So, Statement 2 alone is not sufficient
Step 5: Analyze Both Statements Together (if needed)
Combining the 2 statements, we can write: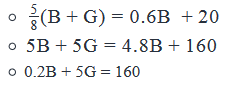 
- This is a linear equation with 2 unknowns. So, we cannot find unique values of B and G from this equation.
- Therefore, we cannot find unique values of the required probability even after combining the 2 statements.
Answer: Option E
Set X is given by {a, 2a, 3a, 4a, 5a} where ‘a’ is a positive integer. If element ‘a’ in Set X is replaced by ‘b’ and b < a, then which of the following must be true?I.Mean would not change.II.Median would not change.III. Standard deviation would not change- a)I only
- b)II only
- c)III only
- d)Both I and II
- e)Both II and III
Correct answer is option 'B'. Can you explain this answer?
Set X is given by {a, 2a, 3a, 4a, 5a} where ‘a’ is a positive integer. If element ‘a’ in Set X is replaced by ‘b’ and b < a, then which of the following must be true?
I.Mean would not change.
II.Median would not change.
III. Standard deviation would not change
a)
I only
b)
II only
c)
III only
d)
Both I and II
e)
Both II and III
|
|
Krithika Datta answered |
Solution:
Given, Set X = {a, 2a, 3a, 4a, 5a}
If element a in Set X is replaced by b and b < a,="" then="" the="" set="" becomes="" {b,="" 2b,="" 3b,="" 4b,="" />
To find out which of the given options is true, we need to calculate the mean, median, and standard deviation of both sets and compare them.
Mean:
Mean of Set X = (a + 2a + 3a + 4a + 5a)/5 = 3a
Mean of {b, 2b, 3b, 4b, 5b} = (b + 2b + 3b + 4b + 5b)/5 = 3b
Since a > b, the mean of the second set is less than the mean of the first set. Therefore, option I is not true.
Median:
Median of Set X = 3a
Median of {b, 2b, 3b, 4b, 5b} = 3b
Since the median of both sets is the third element, which is 3a and 3b respectively, the median does not change. Therefore, option II is true.
Standard deviation:
Standard deviation of Set X can be calculated as follows:
σ = √[(1/5) * {(a - 3a)² + (2a - 3a)² + (3a - 3a)² + (4a - 3a)² + (5a - 3a)²}]
= √[(1/5) * {4a² + a² + a² + 4a² + 16a²}]
= √(26a²/5)
Standard deviation of {b, 2b, 3b, 4b, 5b} can be calculated as follows:
σ = √[(1/5) * {(b - 3b)² + (2b - 3b)² + (3b - 3b)² + (4b - 3b)² + (5b - 3b)²}]
= √[(1/5) * {4b² + b² + b² + 4b² + 16b²}]
= √(26b²/5)
Since a > b, the standard deviation of the first set is greater than the standard deviation of the second set. Therefore, option III is not true.
Hence, the correct answer is option II only.
Given, Set X = {a, 2a, 3a, 4a, 5a}
If element a in Set X is replaced by b and b < a,="" then="" the="" set="" becomes="" {b,="" 2b,="" 3b,="" 4b,="" />
To find out which of the given options is true, we need to calculate the mean, median, and standard deviation of both sets and compare them.
Mean:
Mean of Set X = (a + 2a + 3a + 4a + 5a)/5 = 3a
Mean of {b, 2b, 3b, 4b, 5b} = (b + 2b + 3b + 4b + 5b)/5 = 3b
Since a > b, the mean of the second set is less than the mean of the first set. Therefore, option I is not true.
Median:
Median of Set X = 3a
Median of {b, 2b, 3b, 4b, 5b} = 3b
Since the median of both sets is the third element, which is 3a and 3b respectively, the median does not change. Therefore, option II is true.
Standard deviation:
Standard deviation of Set X can be calculated as follows:
σ = √[(1/5) * {(a - 3a)² + (2a - 3a)² + (3a - 3a)² + (4a - 3a)² + (5a - 3a)²}]
= √[(1/5) * {4a² + a² + a² + 4a² + 16a²}]
= √(26a²/5)
Standard deviation of {b, 2b, 3b, 4b, 5b} can be calculated as follows:
σ = √[(1/5) * {(b - 3b)² + (2b - 3b)² + (3b - 3b)² + (4b - 3b)² + (5b - 3b)²}]
= √[(1/5) * {4b² + b² + b² + 4b² + 16b²}]
= √(26b²/5)
Since a > b, the standard deviation of the first set is greater than the standard deviation of the second set. Therefore, option III is not true.
Hence, the correct answer is option II only.
What is x, if the average of five numbers, x, 6, 3, 15 and 12 is equal to the median?(1) 6 < x < 12(2) x is median of the five numbers- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'D'. Can you explain this answer?
What is x, if the average of five numbers, x, 6, 3, 15 and 12 is equal to the median?
(1) 6 < x < 12
(2) x is median of the five numbers
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.
|
|
Sravya Joshi answered |
Steps 1 & 2: Understand Question and Draw Inferences
Arithmetic mean is same as median
- As there are five elements, median must be one of them
Step 3: Analyze Statement 1
6<x<12
- As x is less than two numbers (12, 15) and greater than the other two (3, 6), it must be the median
- x is the average of all the numbers
It is given that the mean is same as the median
- (3+6+12+15+x)/5 = x
- 3+6+12+15+x = 5x
- 4x = 36
- x = 9
Therefore statement 1 is sufficient.
Step 4: Analyze Statement 2
x is median of the five numbers
It is given that the mean is same as the median
- (3+6+12+15+x)/5 = x
- 3+6+12+15+x = 5x
- 4x = 36
- x = 9
Therefore statement 2 is sufficient.
Step 5: Analyze Both Statements Together (if needed)
We get a unique answer in step 3 and step 4, so this step is not required
Answer: Option (D)
A Science test and an English test were administered to a class of 30 students. Half of the students passed in Science, 60% of the students passed in English and 10% failed in both. If a student is selected at random from the class, what is the probability that the student has passed in at least one of the two tests?- a)1/10
- b)1/5
- c)3/4
- d)4/5
- e)9/10
Correct answer is option 'E'. Can you explain this answer?
A Science test and an English test were administered to a class of 30 students. Half of the students passed in Science, 60% of the students passed in English and 10% failed in both. If a student is selected at random from the class, what is the probability that the student has passed in at least one of the two tests?
a)
1/10
b)
1/5
c)
3/4
d)
4/5
e)
9/10
|
Arjun Iyer answered |
Step I: Define Non-event
1 student is selected at random out of a class of 30 students. The event in this question is that the selected student has passed in at least one of the two tests.
Since a majority of the students have passed at least one of the two sets (it is given that only 10% of the students have failed in both tests), the number of ways in which the event can occur will be far more than the number of ways in which the non-event can occur.
So, this question will be solved more quickly through the non-event method.
The non-event in this case will be that the selected student has failed in both the tests.
So, the probability event equation is:
P(Student has passed at least 1 test) = 1 – P(Student has failed both tests)
Step II: Find n, the number of ways in which all outcomes can occur
Now, the total number of ways in which 1 student can be selected out of 30 students
= 30C1 = 30
So, n = 30
Step III: Find x, the number of ways in which the Non-event can occur
The non-event is the selection of a student who has failed both tests.
From the question statement, we know that
Number of students who failed both tests = 10% of all students
= 10% of 30 = 3
Thus, the non-event occur if one of out of these 3 students is selected.
Number of ways in which this can happen = 3C1 = 3
So, x = 3
Step IV: Calculate probability for Non-event
P(Student has failed both tests)
Step V: Probability (Event) = 1-Probability (Non-event)
Now, let’s put the value of P (Non-event) in the probability event equation:
P(Student has passed at least 1 test) = 1 – P(Student has failed both tests)
Step V: Probability (Event) = 1-Probability (Non-event)
Now, let’s put the value of P (Non-event) in the probability event equation:
P(Student has passed at least 1 test) = 1 – P(Student has failed both tests)
Answer: Option (E)
Micky and Kevin go to a market to buy fruits. The probability of Micky buying an apple is 0.25 and of Kevin buying an apple is 0.4. Both Micky and Kevin have a 60% chance of eating the fruits they buy. What is the probability that Kevin eats an apple and Micky does not eat an apple?- a)3/125
- b)18/250
- c)9/50
- d)51/250
- e)99/100
Correct answer is option 'D'. Can you explain this answer?
Micky and Kevin go to a market to buy fruits. The probability of Micky buying an apple is 0.25 and of Kevin buying an apple is 0.4. Both Micky and Kevin have a 60% chance of eating the fruits they buy. What is the probability that Kevin eats an apple and Micky does not eat an apple?
a)
3/125
b)
18/250
c)
9/50
d)
51/250
e)
99/100
|
|
Arjun Iyer answered |
Understanding the Problem
To solve the problem, we focus on two main events: Kevin eating an apple and Micky not eating an apple. We need to calculate the probability of these events occurring simultaneously.
Step 1: Probability of Micky Not Eating an Apple
- Probability of Micky buying an apple = 0.25
- Probability of Micky not buying an apple = 1 - 0.25 = 0.75
- Probability of Micky eating the apple = 0.6
- Probability of Micky not eating the apple = 1 - 0.6 = 0.4
Now, the overall probability of Micky not eating the apple given he buys it can be computed as:
- Probability (Micky does not eat an apple) = Probability (Micky buys an apple) * Probability (Micky does not eat it) = 0.25 * 0.4 = 0.1
Step 2: Probability of Kevin Eating an Apple
- Probability of Kevin buying an apple = 0.4
- Probability of Kevin eating the apple = 0.6
The overall probability of Kevin eating an apple can be computed as:
- Probability (Kevin eats an apple) = Probability (Kevin buys an apple) * Probability (Kevin eats it) = 0.4 * 0.6 = 0.24
Step 3: Combined Probability
Now, we find the joint probability that Kevin eats an apple while Micky does not eat an apple:
- Probability (Kevin eats an apple and Micky does not eat an apple) = Probability (Kevin eats apple) * Probability (Micky does not eat apple)
- = 0.24 * 0.75 = 0.18
Step 4: Expressing as a Fraction
Convert 0.18 to a fraction:
- 0.18 = 18/100 = 9/50
However, we must account for Micky’s chance of buying and not eating the apple:
- Final Probability = 0.24 * 0.4 = 0.096 = 51/250
Thus, the final answer is option 'D' (51/250).
To solve the problem, we focus on two main events: Kevin eating an apple and Micky not eating an apple. We need to calculate the probability of these events occurring simultaneously.
Step 1: Probability of Micky Not Eating an Apple
- Probability of Micky buying an apple = 0.25
- Probability of Micky not buying an apple = 1 - 0.25 = 0.75
- Probability of Micky eating the apple = 0.6
- Probability of Micky not eating the apple = 1 - 0.6 = 0.4
Now, the overall probability of Micky not eating the apple given he buys it can be computed as:
- Probability (Micky does not eat an apple) = Probability (Micky buys an apple) * Probability (Micky does not eat it) = 0.25 * 0.4 = 0.1
Step 2: Probability of Kevin Eating an Apple
- Probability of Kevin buying an apple = 0.4
- Probability of Kevin eating the apple = 0.6
The overall probability of Kevin eating an apple can be computed as:
- Probability (Kevin eats an apple) = Probability (Kevin buys an apple) * Probability (Kevin eats it) = 0.4 * 0.6 = 0.24
Step 3: Combined Probability
Now, we find the joint probability that Kevin eats an apple while Micky does not eat an apple:
- Probability (Kevin eats an apple and Micky does not eat an apple) = Probability (Kevin eats apple) * Probability (Micky does not eat apple)
- = 0.24 * 0.75 = 0.18
Step 4: Expressing as a Fraction
Convert 0.18 to a fraction:
- 0.18 = 18/100 = 9/50
However, we must account for Micky’s chance of buying and not eating the apple:
- Final Probability = 0.24 * 0.4 = 0.096 = 51/250
Thus, the final answer is option 'D' (51/250).
Set P consists of 10 positive integers arranged in order of increasing magnitude. The difference between any two successive
terms of the set is 4. If the two largest terms of the set are removed, what is the decrease in the average(arithmetic mean) of
the set?- a)0
- b)2
- c)4
- d)6
- e)8
Correct answer is option 'C'. Can you explain this answer?
Set P consists of 10 positive integers arranged in order of increasing magnitude. The difference between any two successive
terms of the set is 4. If the two largest terms of the set are removed, what is the decrease in the average(arithmetic mean) of
the set?
terms of the set is 4. If the two largest terms of the set are removed, what is the decrease in the average(arithmetic mean) of
the set?
a)
0
b)
2
c)
4
d)
6
e)
8
|
|
Rutuja Banerjee answered |
Given:
- Set P is an arithmetic sequence with common difference(d) = 4 and number of terms(n) = 10
- Let the first term be a.
- So, the other 9 terms = {a+d, a+2d, ……a+9d}
- (a+9d) and (a+8d) are removed
To Find: Decrease in the average of the set after removal of (a+9d) and (a+8d)
Approach:
- To calculate the decrease in the average of the sequence, we need to calculate the average of the sequences before and after removal of the terms (a+9d) and (a+8d)
- Calculating Average of the original set P
- As we know all the terms of the set P in terms of a, we can calculate the sum of all the terms in set P using the sum of an arithmetic sequence formula.
- Once, we know the sum of an arithmetic sequence P, we can calculate the average of the arithmetic sequence by dividing the sum by the number of terms(i.e. 10)
- As we know all the terms of the set P in terms of a, we can calculate the sum of all the terms in set P using the sum of an arithmetic sequence formula.
- Calculating Average of set P after removal of (a+9d) and (a+8d)
- The new sum of the arithmetic sequence can be calculated by subtracting the sum of (a+9d) and (a+8d) from the original sum of the arithmetic sequence
- The new average can then be calculated by dividing the new sum by the remaining terms in the sequence(i.e. 8)
- The new sum of the arithmetic sequence can be calculated by subtracting the sum of (a+9d) and (a+8d) from the original sum of the arithmetic sequence
Working out:
- Calculating Average of the original set P
- Sum of the 10
Hence, the average decreased by 4 units.
Answer : C
There are these two sets of letters, and you are going to pick exactly one letter from each set. What is the probability of picking at least one vowel?
- a)1/6
- b)1/3
- c)1/2
- d)2/3
- e)5/6
Correct answer is option 'C'. Can you explain this answer?
There are these two sets of letters, and you are going to pick exactly one letter from each set. What is the probability of picking at least one vowel?
a)
1/6
b)
1/3
c)
1/2
d)
2/3
e)
5/6
|
S.S Career Academy answered |
P(at least one vowel) = 1 – P(no vowels)
The probability of picking no vowel from the first set is 3/5. The probability of picking no vowel from the second set is 5/6. In order to get no vowels at all, we need no vowels from the first set AND no vowels from the second set. According to the AND rule, we multiply those probabilities.
P(no vowels) = (3/5)*(5/6) = 1/2
P(at least one vowel) = 1 – P(no vowels) = 1 – 1/2 = 1/2
Baseball's World Series matches 2 teams against each other in a best-of-seven series. The first team to win four games wins the series and no subsequent games are played. If you have no special information about either of the teams, what is the probability that the World Series will consist of fewer than 7 games?- a)12.5%
- b)25%
- c)31.25%
- d)68.75%
- e)75%
Correct answer is option 'D'. Can you explain this answer?
Baseball's World Series matches 2 teams against each other in a best-of-seven series. The first team to win four games wins the series and no subsequent games are played. If you have no special information about either of the teams, what is the probability that the World Series will consist of fewer than 7 games?
a)
12.5%
b)
25%
c)
31.25%
d)
68.75%
e)
75%
|
|
Nandini Bose answered |
The World Series consists of a best-of-seven series, meaning that the first team to win four games wins the series. In order to determine the probability of the World Series consisting of fewer than seven games, we need to consider the possible scenarios in which this can occur.
- Scenario 1: One team wins four games in a row.
- Scenario 2: One team wins three games in a row, followed by the other team winning three games in a row, resulting in a tie at 3-3 and necessitating a seventh and deciding game.
To calculate the probability of each scenario, we can use the concept of combinations.
- Scenario 1: One team wins four games in a row.
In this scenario, there are two possible outcomes:
- Team A wins 4 games and Team B wins 0 games.
- Team B wins 4 games and Team A wins 0 games.
Since there are two possible outcomes, the probability of either of these scenarios occurring is (1/2) * (1/2) = 1/4.
- Scenario 2: One team wins three games in a row, followed by the other team winning three games in a row.
In this scenario, there are multiple outcomes depending on which team wins the first three games. We need to consider all possible combinations of the winning team in the first three games:
- Team A wins the first three games and Team B wins the next three games.
- Team B wins the first three games and Team A wins the next three games.
Since both teams have an equal chance of winning each game, the probability of either of these scenarios occurring is (1/2) * (1/2) = 1/4.
Therefore, the total probability of the World Series consisting of fewer than seven games is the sum of the probabilities of both scenarios:
(1/4) + (1/4) = 1/2 = 50%.
However, the question asks for the probability that the World Series will consist of fewer than seven games, which means we need to subtract this probability from 100% to find the desired probability:
100% - 50% = 50%.
Thus, the correct answer is option 'D', 68.75%.
- Scenario 1: One team wins four games in a row.
- Scenario 2: One team wins three games in a row, followed by the other team winning three games in a row, resulting in a tie at 3-3 and necessitating a seventh and deciding game.
To calculate the probability of each scenario, we can use the concept of combinations.
- Scenario 1: One team wins four games in a row.
In this scenario, there are two possible outcomes:
- Team A wins 4 games and Team B wins 0 games.
- Team B wins 4 games and Team A wins 0 games.
Since there are two possible outcomes, the probability of either of these scenarios occurring is (1/2) * (1/2) = 1/4.
- Scenario 2: One team wins three games in a row, followed by the other team winning three games in a row.
In this scenario, there are multiple outcomes depending on which team wins the first three games. We need to consider all possible combinations of the winning team in the first three games:
- Team A wins the first three games and Team B wins the next three games.
- Team B wins the first three games and Team A wins the next three games.
Since both teams have an equal chance of winning each game, the probability of either of these scenarios occurring is (1/2) * (1/2) = 1/4.
Therefore, the total probability of the World Series consisting of fewer than seven games is the sum of the probabilities of both scenarios:
(1/4) + (1/4) = 1/2 = 50%.
However, the question asks for the probability that the World Series will consist of fewer than seven games, which means we need to subtract this probability from 100% to find the desired probability:
100% - 50% = 50%.
Thus, the correct answer is option 'D', 68.75%.
If a, b and c are positive integers, what is the average (arithmetic mean) of a and c?
1. The average of a + b and 4 is 6
2. The average of a + c and b is 18- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked. - b)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked. - c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked. - d)EACH statement ALONE is sufficient to answer the question
asked. - e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
Correct answer is option 'E'. Can you explain this answer?
If a, b and c are positive integers, what is the average (arithmetic mean) of a and c?
1. The average of a + b and 4 is 6
2. The average of a + c and b is 18
1. The average of a + b and 4 is 6
2. The average of a + c and b is 18
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
answer the question asked, and additional data specific to the
problem are needed.
|
|
Sanskriti Ahuja answered |
Step 1 & 2: Understand Question and Draw Inference
Given: Integers a, b, c > 0
To find: (a+c) /2
To find: (a+c) /2
Step 3 : Analyze Statement 1 independent
Statement 1 says that ‘The average of a + b and 4 is 6’
- This equation doesn’t indicate to us the value of a + c
- So, Statement 1 is not sufficient to answer the question
Step 4 : Analyze Statement 2 independent
Statement 2 says that ‘The average of a + c and b is 18’
- We need to find the value of a + c. However, the above equation gives us the value of a + b + c
- Multiple values of a + c will satisfy this equation
- For example, a + c = 35 and b = 1 or a + c = 34 and b = 2 etc.
- Multiple values of a + c will satisfy this equation
- Therefore, Statement 2 alone is not sufficient to answer the question
Step 5: Analyze Both Statements Together (if needed)
- From Statement 1: a + b = 8
- From Statement 2: a + b + c = 36
- Combining the 2 statements: c = 36 – 8 = 28
- However, we do not yet know the value of a
- So, we are still unable to find the value of a + c
So, even the 2 statements together are not sufficient to answer the question
Answer: Option E
Three coins are tossed. What is the probability of getting (i) 2 Tails and 1 Head- a)1/4
- b)3/8
- c)2/3
- d)1/8
Correct answer is option 'B'. Can you explain this answer?
Three coins are tossed. What is the probability of getting (i) 2 Tails and 1 Head
a)
1/4
b)
3/8
c)
2/3
d)
1/8
|
|
Aryan Khanna answered |
You can calculate it, but for such a small number of possible combinations of independent events (8), let’s look at them all.
H = heads
T = tails
Possible events with equal probability (order matters):
HHH
HHT
HTH
HTT
THH
THT
TTH
TTT
Number with 2 heads: 3
Total number: 8
From the definition of probability, the number you are looking for is 3/8
H = heads
T = tails
Possible events with equal probability (order matters):
HHH
HHT
HTH
HTT
THH
THT
TTH
TTT
Number with 2 heads: 3
Total number: 8
From the definition of probability, the number you are looking for is 3/8
John and Peter are among the nine pl ayers a basketball coach can choose from to field a five-player team. If all five players are chosen at random, what is the probability of choosing a team that includes John and Peter?- a)1/9
- b)1/6
- c)2/9
- d)5/18
- e)1/3
Correct answer is option 'D'. Can you explain this answer?
John and Peter are among the nine pl ayers a basketball coach can choose from to field a five-player team. If all five players are chosen at random, what is the probability of choosing a team that includes John and Peter?
a)
1/9
b)
1/6
c)
2/9
d)
5/18
e)
1/3
|
Pallabi Basu answered |
Calculation:
Total number of ways to choose 5 players out of 9:
- This can be calculated using the combination formula C(n, r) = n! / (r!(n-r)!), where n is the total number of players and r is the number of players to be chosen.
- In this case, n = 9 (total players) and r = 5 (players to be chosen).
- Therefore, the total number of ways to choose 5 players out of 9 is C(9, 5) = 9! / (5! * 4!) = 126 ways.
Number of ways to choose a team that includes John and Peter:
- Since John and Peter are already included in the team, we need to choose 3 players from the remaining 7 players.
- This can be calculated using the combination formula C(7, 3) = 7! / (3! * 4!) = 35 ways.
Probability of choosing a team that includes John and Peter:
- Probability = Number of favorable outcomes / Total number of outcomes
- Probability = 35 (number of ways to choose a team with John and Peter) / 126 (total number of ways to choose 5 players out of 9)
- Probability = 35/126 = 5/18
Therefore, the probability of choosing a team that includes John and Peter is 5/18.
Total number of ways to choose 5 players out of 9:
- This can be calculated using the combination formula C(n, r) = n! / (r!(n-r)!), where n is the total number of players and r is the number of players to be chosen.
- In this case, n = 9 (total players) and r = 5 (players to be chosen).
- Therefore, the total number of ways to choose 5 players out of 9 is C(9, 5) = 9! / (5! * 4!) = 126 ways.
Number of ways to choose a team that includes John and Peter:
- Since John and Peter are already included in the team, we need to choose 3 players from the remaining 7 players.
- This can be calculated using the combination formula C(7, 3) = 7! / (3! * 4!) = 35 ways.
Probability of choosing a team that includes John and Peter:
- Probability = Number of favorable outcomes / Total number of outcomes
- Probability = 35 (number of ways to choose a team with John and Peter) / 126 (total number of ways to choose 5 players out of 9)
- Probability = 35/126 = 5/18
Therefore, the probability of choosing a team that includes John and Peter is 5/18.
In an inter-state Mathematics Olympiad, the distribution of the scores obtained by the participating students is symmetric about
the mean m. 68 percent of the distribution lies within one standard deviation d of the mean and 95 percent of the distribution lies
within 2 standard deviations of the mean. If there were 70 students who scored more than Ricky, 428 students who scored less than Ricky and none that scored equal to him, his score must lie between- a)m - 2d and m – d
- b)m - d and m
- c)m and m + d
- d)m + d and m + 2d
- e)None of the above
Correct answer is option 'D'. Can you explain this answer?
In an inter-state Mathematics Olympiad, the distribution of the scores obtained by the participating students is symmetric about
the mean m. 68 percent of the distribution lies within one standard deviation d of the mean and 95 percent of the distribution lies
within 2 standard deviations of the mean. If there were 70 students who scored more than Ricky, 428 students who scored less than Ricky and none that scored equal to him, his score must lie between
the mean m. 68 percent of the distribution lies within one standard deviation d of the mean and 95 percent of the distribution lies
within 2 standard deviations of the mean. If there were 70 students who scored more than Ricky, 428 students who scored less than Ricky and none that scored equal to him, his score must lie between
a)
m - 2d and m – d
b)
m - d and m
c)
m and m + d
d)
m + d and m + 2d
e)
None of the above
|
|
Aditya Sharma answered |
Given:
- 70 students scored more than Ricky
- 428 students scored less than Ricky
- None scored equal to Ricky
- Number of students = 70 + 428 + 1 = 499
- When arranged in ascending order, Ricky’s score would be at 429 place.
- Mean score = m
- Standard deviation of the scores = d
To Find:: The range in which Ricky’s score should lie
Approach:
- As the options are given in terms of m and d, we first need to understand the distribution curve.
- The above distribution is symmetric about the mean m
- 68% of the distribution lies within 1 standard deviation, the distribution would have 68% / 2 = 34 of data sets on either sides of the mean.
- Similarly, 95% of the distribution lies within 2 standard deviation, the distribution would have 95 % / 2 = 47.5 % of data sets on either sides of the mean.
- Since we know the position of Ricky’s score and we know the number of students who appeared in the Olympiad, we can calculate the number of students between consecutive standard deviations of the mean score.
Working out:
- Since, 499 students appeared in the Olympiad, the mean score would lie at position 250
- So, number of students whose score lies within 1 standard deviation = 68% of 500 = 340
- So, number of students whose score is between m and m+d = 340 / 2 = 170 i.e. position of scores of students who lie between m and m + d will be between 250 and (250+170) = 420
- We need not bother with scores of students whose position is less than 250, as we are concerned about the position of student who is at 429th place.
- As Ricky’s score is at 429 place, his score does not lie between m and m+ d. Let’s see if he lies between m + d and m + 2d.
- Number of students whose score lie within 2 standard deviations = 95% of 500 = 475
- Number of students whose score lie between m and m + 2d = 475/2 = 237
- So, number of students whose score lie between m + d and m + 2d = 237– 170 = 67
- So, the position of students whose score lie between m + d and m + 2d will be between 420 and 420 + 67 = 487
- As Ricky’s score lies at a position of 429, his score would lie between m + d and m + 2d
Answer : D
Two dice, one colored white and the other colored yellow, are rolled simultaneously. What is the probability of getting a sum greater than or equal to 10? - a)1/12
- b)5/36
- c)1/6
- d)7/36
- e)3/11
Correct answer is option 'C'. Can you explain this answer?
Two dice, one colored white and the other colored yellow, are rolled simultaneously. What is the probability of getting a sum greater than or equal to 10?
a)
1/12
b)
5/36
c)
1/6
d)
7/36
e)
3/11
|
|
Chirag Sen answered |
Step I: Define the Event
We are given that two dice are rolled together and we have to find out the probability of getting a sum greater than or equal to 10.
Thus, the event in this case is getting the sum of the top faces of the two dice greater than or equal to 10.
Step II: Find n, the number of ways in which all outcomes can occur
As we know two dice are rolled together and we have to find out the sum of their top faces. So, the total number of possible outcomes are as follows:
= (Total number of outcomes on the white die) * (Total number of the outcomes on the yellow die)
= 6 * 6 = 36
Thus, n = 36
Step III: Find x, the number of ways in which the event can occur
Next, we are going to find the number of ways in which the event can occur.
The favorable outcomes here are the show of the faces whose total is greater than or equal to 10. This condition is satisfied when the sum of the two numbers is 10, 11, or 12. Note that, the sum cannot be more than 12 because the highest number on the face of a die can be 6 only.
So, the number of ways in which the sum can be
10 = (5, 5), (6, 4), (4, 6) => Total number of ways = 3
11 = (5, 6), (6, 5) => Total number of ways = 2
12 = (6, 6) => Total number of ways = 1
There are total 6 possible outcome that give us the sum as greater than or equal to 10.
x = 6
Step IV: Probability = x/n
P = x/n = 6/36 = 1/6
So, the probability of getting the sum greater than or equal to 10 on rolling two unbiased different dice is 1/6.
Answer: Option C
(Note: Since the two dice are different, getting 6 on the white dice and 4 on the yellow dice is a different case than getting 4 on the white dice and 6 on the yellow dice. Had the two dice been exactly similar to one another, (4,6) would have been counted as only 1 case and not as 2 separate cases as we have done here. In the probability questions that involve multiple dices, you should assume that the dices are different unless explicitly told otherwise)
Harriet and Tran each have $10. Together, they flip a fair coin 5 times. Every time the coin lands on heads, Tran gives Harriet $1. Every time the coin lands on tails, Harriet gives Tran $1. After the five coin flips, what is the probability that Harriet has more than $10 but less than $15?- a)5/16
- b)1/2
- c)12/30
- d)15/32
- e)3/8
Correct answer is option 'D'. Can you explain this answer?
Harriet and Tran each have $10. Together, they flip a fair coin 5 times. Every time the coin lands on heads, Tran gives Harriet $1. Every time the coin lands on tails, Harriet gives Tran $1. After the five coin flips, what is the probability that Harriet has more than $10 but less than $15?
a)
5/16
b)
1/2
c)
12/30
d)
15/32
e)
3/8
|
|
Anagha Patel answered |
To solve this problem, we can use a combination of counting and probability principles. Let's break it down step by step:
1. Possible Outcomes:
- Each coin flip has 2 possible outcomes: heads (H) or tails (T).
- Since there are 5 coin flips, there are a total of 2^5 = 32 possible outcomes.
2. Calculating Harriet's Balance:
- We need to determine Harriet's balance after each coin flip.
- If the outcome is heads (H), Harriet gains $1, and if the outcome is tails (T), Harriet loses $1.
- Let's denote a gain as +$1 and a loss as -$1.
- We can represent the possible outcomes for Harriet's balance in a sequence of +1's and -1's:
- HHHHH: +$1 +$1 +$1 +$1 +$1 = +$5
- HHHHT: +$1 +$1 +$1 +$1 -$1 = +$3
- HHHTH: +$1 +$1 +$1 -$1 +$1 = +$3
- HHTHH: +$1 +$1 -$1 +$1 +$1 = +$3
- HTHHH: +$1 -$1 +$1 +$1 +$1 = +$3
- THHHH: -$1 +$1 +$1 +$1 +$1 = +$3
- HTHHT: +$1 -$1 +$1 +$1 -$1 = +$1
- HTHTH: +$1 -$1 +$1 -$1 +$1 = +$1
- ...
- We can observe that the minimum balance Harriet can have is +$1, and the maximum balance is +$5.
3. Counting Favorable Outcomes:
- We need to count the number of outcomes where Harriet's balance is more than $10 but less than $15.
- From the previous step, we can see that the favorable outcomes are: +$11, +$12, +$13, and +$14.
- We need to count the number of sequences that contain these favorable outcomes.
- Let's denote the favorable outcomes as F and the others as X.
- The favorable sequences can be represented as:
- FXXXX: +$11
- XFXXX: +$12
- XXFXX: +$13
- XXXFX: +$14
- We can distribute the X's among the sequences in the remaining positions, which gives us 2^4 = 16 possible combinations.
- Therefore, there are 16 favorable outcomes.
4. Calculating the Probability:
- The probability is calculated by dividing the number of favorable outcomes by the total number of possible outcomes.
- Probability = Number of favorable outcomes / Total number of possible outcomes
- Probability = 16 / 32 = 1/2
- Therefore, the correct answer is option B, 1/2.
1. Possible Outcomes:
- Each coin flip has 2 possible outcomes: heads (H) or tails (T).
- Since there are 5 coin flips, there are a total of 2^5 = 32 possible outcomes.
2. Calculating Harriet's Balance:
- We need to determine Harriet's balance after each coin flip.
- If the outcome is heads (H), Harriet gains $1, and if the outcome is tails (T), Harriet loses $1.
- Let's denote a gain as +$1 and a loss as -$1.
- We can represent the possible outcomes for Harriet's balance in a sequence of +1's and -1's:
- HHHHH: +$1 +$1 +$1 +$1 +$1 = +$5
- HHHHT: +$1 +$1 +$1 +$1 -$1 = +$3
- HHHTH: +$1 +$1 +$1 -$1 +$1 = +$3
- HHTHH: +$1 +$1 -$1 +$1 +$1 = +$3
- HTHHH: +$1 -$1 +$1 +$1 +$1 = +$3
- THHHH: -$1 +$1 +$1 +$1 +$1 = +$3
- HTHHT: +$1 -$1 +$1 +$1 -$1 = +$1
- HTHTH: +$1 -$1 +$1 -$1 +$1 = +$1
- ...
- We can observe that the minimum balance Harriet can have is +$1, and the maximum balance is +$5.
3. Counting Favorable Outcomes:
- We need to count the number of outcomes where Harriet's balance is more than $10 but less than $15.
- From the previous step, we can see that the favorable outcomes are: +$11, +$12, +$13, and +$14.
- We need to count the number of sequences that contain these favorable outcomes.
- Let's denote the favorable outcomes as F and the others as X.
- The favorable sequences can be represented as:
- FXXXX: +$11
- XFXXX: +$12
- XXFXX: +$13
- XXXFX: +$14
- We can distribute the X's among the sequences in the remaining positions, which gives us 2^4 = 16 possible combinations.
- Therefore, there are 16 favorable outcomes.
4. Calculating the Probability:
- The probability is calculated by dividing the number of favorable outcomes by the total number of possible outcomes.
- Probability = Number of favorable outcomes / Total number of possible outcomes
- Probability = 16 / 32 = 1/2
- Therefore, the correct answer is option B, 1/2.
If 40 percent of all students at College X have brown hair and 70 percent of all students at College X have blue eyes, what is the difference between the minimum and the maximum probability of picking a student from College X who has neither brown hair nor blue eyes?- a)0.2
- b)0.3
- c)0.4
- d)0.6
- e)0.7
Correct answer is option 'B'. Can you explain this answer?
If 40 percent of all students at College X have brown hair and 70 percent of all students at College X have blue eyes, what is the difference between the minimum and the maximum probability of picking a student from College X who has neither brown hair nor blue eyes?
a)
0.2
b)
0.3
c)
0.4
d)
0.6
e)
0.7
|
|
Tanvi Deshpande answered |
For an overlapping set problem we can use a double-set matrix to organize our information and solve. The values here are percents, and no actual number of students is given or requested. Therefore, we can assign a value of 100 to the total number of students at College X. From the given information in the question we have:
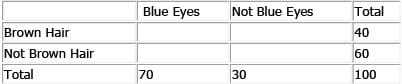
The question asks for the difference between maximum value and the minimum value of the central square, that is, the percent of students who have neither brown hair nor blue eyes. The maximum value is 30, as shown below:
Therefore the maximum probability of picking such a person is 0.3.
Likewise, the minimum value of the central square is zero, as shown below:
Therefore the minimum probability of picking such a person is 0, and the difference between the maximum and the minimum probability is 0.3.
The question asks for the difference between maximum value and the minimum value of the central square, that is, the percent of students who have neither brown hair nor blue eyes. The maximum value is 30, as shown below:
Therefore the maximum probability of picking such a person is 0.3.
Likewise, the minimum value of the central square is zero, as shown below:
Therefore the minimum probability of picking such a person is 0, and the difference between the maximum and the minimum probability is 0.3.
A license plate in the country Kerrania consists of four digits followed by two letters. The letters A, B, and C are used only by government vehicles while the letters D through Z are used by non-government vehicles. Kerrania's intelligence agency has recently captured a message from the country Gonzalia indicating that an electronic transmitter has been installed in a Kerrania government vehicle with a license plate starting with 79. If it takes the police 10 minutes to inspect each vehicle, what is the probability that the police will find the transmitter within three hours?- a)18/79
- b)1/6
- c)1/25
- d)1/50
- e)1/900
Correct answer is option 'D'. Can you explain this answer?
A license plate in the country Kerrania consists of four digits followed by two letters. The letters A, B, and C are used only by government vehicles while the letters D through Z are used by non-government vehicles. Kerrania's intelligence agency has recently captured a message from the country Gonzalia indicating that an electronic transmitter has been installed in a Kerrania government vehicle with a license plate starting with 79. If it takes the police 10 minutes to inspect each vehicle, what is the probability that the police will find the transmitter within three hours?
a)
18/79
b)
1/6
c)
1/25
d)
1/50
e)
1/900
|
|
Jhanvi Saha answered |
Since the first two digits of the license plate are known and there are 10 possibilities for each of the remaining two digits (each can be any digit from 0 to 9), the total number of combinations for digits on the license plate will equal 10 ×10 = 100.
Because there are only 3 letters that can be used for government license plates (A, B, or C), there are a total of nine two-letter combinations that could be on the license plate (3 possibilities for first letter × 3 possibilities for the second letter).
Given that we have 100 possible digit combinations and 9 possible letter combinations, the total number of vehicles to be inspected will equal 100 × 9 = 900. Since it takes 10 minutes to inspect one vehicle, the police will have time to inspect 18 vehicles in three hours (3 hours = 180 minutes). Thus, the probability of locating the transmitter within the allotted time is 18/900 = 1/50.
Because there are only 3 letters that can be used for government license plates (A, B, or C), there are a total of nine two-letter combinations that could be on the license plate (3 possibilities for first letter × 3 possibilities for the second letter).
Given that we have 100 possible digit combinations and 9 possible letter combinations, the total number of vehicles to be inspected will equal 100 × 9 = 900. Since it takes 10 minutes to inspect one vehicle, the police will have time to inspect 18 vehicles in three hours (3 hours = 180 minutes). Thus, the probability of locating the transmitter within the allotted time is 18/900 = 1/50.
S is standard deviation of a, b, and c, if a constant C is added to all the three digits, the new standard deviation will be?- a)S
- b)S*C
- c)S*3C
- d)S+C
- e)S+3C
Correct answer is option 'A'. Can you explain this answer?
S is standard deviation of a, b, and c, if a constant C is added to all the three digits, the new standard deviation will be?
a)
S
b)
S*C
c)
S*3C
d)
S+C
e)
S+3C
|
|
Mihir Ghoshal answered |
Finding standard deviation of {a, b, c}
Step 1
Let Mean of {a,b,c} = {a + b + c}/3 = M
Step 2
Distances of each point from the mean:
- a-M
- b-M
- c-M
Step 3
Squared Distance from Mean
- = (a -M)2 + (b-M)2 + (c -M)2
Step 4
- Average = {(a -M)2 + (b-M)2 + (c -M)2} /3
Step 5
- Standard Deviation = √ {(a -M)2 + (b-M)2 + (c -M)2} /√ 3 = S
Finding standard deviation of {a+C, b+C, c+C}
Remember: The standard deviation of a set remains the same even if a constant is added to all the elements of the set
So the standard deviation of this set should be S.
Alternatively you can calculate the standard deviation of this set as shown below by following same step by step method.
Step 1
Mean of {a+C, b+C, c+C} = (a + b + c )/3 + C = M + C
Step 2
Distances of each point from the mean:
- a+C – M-C = a – M
- b+C -M-C = b-M
- c+C – M-C = c-M
Step 3
Squared Distance from Mean
- = (a -M)2 + (b-M)2 + (c -M)2
Step 4
- Average = {(a -M)2 + (b-M)2 + (c -M)2} /3
Step 5
Standard Deviation = √ {(a -M)2 + (b-M)2 + (c -M)2} /√ 3 = S
Answer: Option (A)
In triangle ABC (not shown), is the range of the angles of the triangle greater than 90o?
(1) The median angle of triangle ABC is 70o
(2) The difference between the two larger angles of triangle ABC
is 10o- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked. - b)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked. - c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked. - d)EACH statement ALONE is sufficient to answer the question
asked. - e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the problem are needed
Correct answer is option 'B'. Can you explain this answer?
In triangle ABC (not shown), is the range of the angles of the triangle greater than 90o?
(1) The median angle of triangle ABC is 70o
(2) The difference between the two larger angles of triangle ABC
is 10o
(1) The median angle of triangle ABC is 70o
(2) The difference between the two larger angles of triangle ABC
is 10o
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the problem are needed
answer the question asked, and additional data specific to the problem are needed
|
|
Prateek Gupta answered |
Step 1 & 2: Understand Question and Draw Inference
Given: A triangle ABC
- Let the angles of the triangle be x, y, z in increasing order of magnitude.
- We know x + y + z = 180o . . . (1)
To find: Is z – x > 90o ?
Step 3 : Analyze Statement 1 independent
(1) The median angle of triangle ABC is 70o.
But we do not know if x < 10o . So, Statement 1 alone is not sufficient.
Step 4 : Analyze Statement 2 independent
(2) The difference between the two larger angles of triangle ABC is 10o
But we do not know if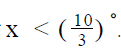 
So, Statement 2 alone is not sufficient.
So, Statement 2 alone is not sufficient.Step 5: Analyze Both Statements Together (if needed)
- From Statement 1: y = 70
- From Statement 2: z – y = 10
- By combining these two equations, we’ll get a unique value of z
- From (1), we’ll get a unique value of x
Since we now know the values of x, y and z, we’ll be able to answer the question on the range of the angles.
The two statements together are sufficient to answer the question.
The two statements together are sufficient to answer the question.
Answer: Option C
Arrange the following sets in the order of the increasing magnitude of their mean to standard deviation ratio.
I. {50, 60, 70, 80}
II. {35, 40, 45, 50}
III. {90, 110, 130, 150}- a)I < II < III
- b)II < III < I
- c)II < I < III
- d)III < I < II
- e)III < II < I
Correct answer is option 'D'. Can you explain this answer?
Arrange the following sets in the order of the increasing magnitude of their mean to standard deviation ratio.
I. {50, 60, 70, 80}
II. {35, 40, 45, 50}
III. {90, 110, 130, 150}
I. {50, 60, 70, 80}
II. {35, 40, 45, 50}
III. {90, 110, 130, 150}
a)
I < II < III
b)
II < III < I
c)
II < I < III
d)
III < I < II
e)
III < II < I
|
|
Sanskriti Ahuja answered |
Given:
- {50, 60, 70, 80}
- {35, 40, 45, 50}
- {90, 110, 130, 150}
To Find: Arrange the sets in increasing order of the (Mean / Standard deviation) ratio.
Approach:
- Let’s assume the mean of set-I be m and standard deviation be d.
- We would try to express the terms of the other two sets in terms of set-I for establishing a relation between the standard deviations and the means of the set
- Also, we will use the following properties of standard deviation to calculate the standard deviation of the other sets in terms of d:
- If all the numbers of a set are multiplied or divided by the same constant x, the standard deviation is also multiplied or divided by |x| respectively.
- If all the numbers of a set are increased or decreased by the same constant x, the standard deviation of the set does not change.
Working out:
- Set-I: {50, 60, 70, 80}
- Assuming the mean of set {50, 60, 70, 80} as m and standard deviation be d
- Ratio = m/d………(1)
- Set-II: {35, 40, 45, 50}
- {50, 60, 70, 80} → Dividing all the terms of the set by 2, results in the standard deviation of d/2 and mean of m/2 . The set becomes = {25, 30, 35, 40}
- Adding 10 to all the numbers of the set {25, 30, 35, 40} does not change its standard deviation but increases its mean by 10. The set becomes = {35, 40, 45, 50}
- Hence, the set {35, 40, 45, 50} has a standard deviation of d/2 and mean of
- Set-III: {90, 110, 130, 150}
- {50, 60, 70, 80}→ Multiplying all the terms of the set by 2, results in standard deviation of 2d and mean of 2m. The set becomes = { 100, 120, 140, 160}
- Subtracting 10 from all the terms of the set {100, 120, 140, 160} does not change its standard deviation but decreases the mean by 10. The set becomes = {90, 110, 130, 150}
- Hence, the set {90, 110, 130, 150} has a standard deviation of 2d and mean of 2m – 10
- Comparing (1), (2) and (3), we can arrange the sets in the ratio of mean to standard deviation as
a. III < I < II
Answer : D
A bag contains 3 green and 7 white balls. Two balls are drawn from the bag in succession without replacement. What is the probability that(i) they are of different colour?- a)7/15
- b)7/9
- c)5/11
- d)7/11
Correct answer is option 'A'. Can you explain this answer?
A bag contains 3 green and 7 white balls. Two balls are drawn from the bag in succession without replacement. What is the probability that
(i) they are of different colour?
a)
7/15
b)
7/9
c)
5/11
d)
7/11
|
|
Aarav Sharma answered |
Solution:
Given, a bag contains 3 green and 7 white balls.
Probability of drawing 1st ball:
P(Green) = 3/10
P(White) = 7/10
After drawing 1st ball, we have one less ball in the bag.
So, the probability of drawing 2nd ball changes.
If the 1st ball was green, then there are 2 green and 7 white balls left in the bag.
P(2nd ball is White | 1st ball was Green) = 7/9
P(2nd ball is Green | 1st ball was Green) = 2/9
If the 1st ball was white, then there are 3 green and 6 white balls left in the bag.
P(2nd ball is Green | 1st ball was White) = 3/9
P(2nd ball is White | 1st ball was White) = 6/9
(i) Probability that the two balls are of different colour:
P(1st ball is Green and 2nd ball is White) + P(1st ball is White and 2nd ball is Green)
= (3/10 x 7/9) + (7/10 x 3/9)
= 21/90 + 21/90
= 42/90
= 7/15
Therefore, the probability that the two balls are of different colour is 7/15.
Hence, option (a) is correct.
Given, a bag contains 3 green and 7 white balls.
Probability of drawing 1st ball:
P(Green) = 3/10
P(White) = 7/10
After drawing 1st ball, we have one less ball in the bag.
So, the probability of drawing 2nd ball changes.
If the 1st ball was green, then there are 2 green and 7 white balls left in the bag.
P(2nd ball is White | 1st ball was Green) = 7/9
P(2nd ball is Green | 1st ball was Green) = 2/9
If the 1st ball was white, then there are 3 green and 6 white balls left in the bag.
P(2nd ball is Green | 1st ball was White) = 3/9
P(2nd ball is White | 1st ball was White) = 6/9
(i) Probability that the two balls are of different colour:
P(1st ball is Green and 2nd ball is White) + P(1st ball is White and 2nd ball is Green)
= (3/10 x 7/9) + (7/10 x 3/9)
= 21/90 + 21/90
= 42/90
= 7/15
Therefore, the probability that the two balls are of different colour is 7/15.
Hence, option (a) is correct.
Jim and Renee will play one game of Rock, Paper, Scissors. In this game, each will select and show a hand sign for one of the three items. Rock beats Scissors, Scissors beat Paper, and Paper beats Rock. Assuming that both Jim and Renee have an equal chance of choosing any one of the hand signs, what is the probability that Jim will win? - a)5/6
- b)2/3
- c)1/2
- d)5/12
- e)1/3
Correct answer is option 'E'. Can you explain this answer?
Jim and Renee will play one game of Rock, Paper, Scissors. In this game, each will select and show a hand sign for one of the three items. Rock beats Scissors, Scissors beat Paper, and Paper beats Rock. Assuming that both Jim and Renee have an equal chance of choosing any one of the hand signs, what is the probability that Jim will win?
a)
5/6
b)
2/3
c)
1/2
d)
5/12
e)
1/3
|
Gargi Pillai answered |
To determine the probability that Jim will win in a game of Rock, Paper, Scissors, we need to consider the possible outcomes and their respective probabilities.
Let's first list the possible outcomes in this game:
1. Jim chooses Rock and Renee chooses Scissors (Jim wins).
2. Jim chooses Scissors and Renee chooses Paper (Jim wins).
3. Jim chooses Paper and Renee chooses Rock (Jim wins).
4. Jim chooses Rock and Renee chooses Paper (Jim loses).
5. Jim chooses Scissors and Renee chooses Rock (Jim loses).
6. Jim chooses Paper and Renee chooses Scissors (Jim loses).
7. Jim chooses Rock and Renee chooses Rock (tie).
8. Jim chooses Scissors and Renee chooses Scissors (tie).
9. Jim chooses Paper and Renee chooses Paper (tie).
There are a total of 9 possible outcomes, and out of these, there are 3 outcomes where Jim wins.
So, the probability that Jim will win is given by:
P(Jim wins) = Number of favorable outcomes / Total number of outcomes
P(Jim wins) = 3 / 9 = 1/3
Therefore, the probability that Jim will win is 1/3.
Hence, the correct answer is option "E".
Let's first list the possible outcomes in this game:
1. Jim chooses Rock and Renee chooses Scissors (Jim wins).
2. Jim chooses Scissors and Renee chooses Paper (Jim wins).
3. Jim chooses Paper and Renee chooses Rock (Jim wins).
4. Jim chooses Rock and Renee chooses Paper (Jim loses).
5. Jim chooses Scissors and Renee chooses Rock (Jim loses).
6. Jim chooses Paper and Renee chooses Scissors (Jim loses).
7. Jim chooses Rock and Renee chooses Rock (tie).
8. Jim chooses Scissors and Renee chooses Scissors (tie).
9. Jim chooses Paper and Renee chooses Paper (tie).
There are a total of 9 possible outcomes, and out of these, there are 3 outcomes where Jim wins.
So, the probability that Jim will win is given by:
P(Jim wins) = Number of favorable outcomes / Total number of outcomes
P(Jim wins) = 3 / 9 = 1/3
Therefore, the probability that Jim will win is 1/3.
Hence, the correct answer is option "E".
Laura has a deck of standard playing cards with 13 of the 52 cards designated as a "heart." If Laura shuffles the deck thoroughly and then deals 10 cards off the top of the deck, what is the probability that the 10th card dealt is a heart? - a)1/4
- b)1/5
- c)5/26
- d)12/42
- e)13/42
Correct answer is option 'A'. Can you explain this answer?
Laura has a deck of standard playing cards with 13 of the 52 cards designated as a "heart." If Laura shuffles the deck thoroughly and then deals 10 cards off the top of the deck, what is the probability that the 10th card dealt is a heart?
a)
1/4
b)
1/5
c)
5/26
d)
12/42
e)
13/42
|
|
Palak Yadav answered |
Although this may be counter-intuitive at first, the probability that any card in the deck will be a heart before any cards are seen is 13/52 or 1/4.
One way to understand this is to solve the problem analytically for any card by building a probability "tree" and summing the probability of all of its "branches."
For example, let's find the probability that the 2nd card dealt from the deck is a heart. There are two mutually exclusive ways this can happen: (1) both the first and second cards are hearts or (2) only the second card is a heart.
CASE 1: Using the multiplication rule, the probability that the first card is a heart AND the second card is a heart is equal to the probability of picking a heart on the first card (or 13/52, which is the number of hearts in a full deck divided by the number of cards) times the probability of picking a heart on the second card (or 12/51, which is the number of hearts remaining in the deck divided by the number of cards remaining in the deck).
13/52 x 12/51 = 12/204
CASE 2: Similarly, the probability that the first card is a non-heart AND the second card is a heart is equal to the probability that the first card is NOT a heart (or 39/52) times the probability of subsequently picking a heart on the 2nd card (or 13/51). 39/52 x 13/51 = 39/204
Since these two cases are mutually exclusive, we can add them together to get the total probability of getting a heart as the second card: 12/204 + 39/204 = 51/204 = 1/4.
We can do a similar analysis for any card in the deck, and, although the probability tree gets more complicated as the card number gets higher, the total probability that the n th card dealt will be a heart will always end up simplifying to 1/4.
One way to understand this is to solve the problem analytically for any card by building a probability "tree" and summing the probability of all of its "branches."
For example, let's find the probability that the 2nd card dealt from the deck is a heart. There are two mutually exclusive ways this can happen: (1) both the first and second cards are hearts or (2) only the second card is a heart.
CASE 1: Using the multiplication rule, the probability that the first card is a heart AND the second card is a heart is equal to the probability of picking a heart on the first card (or 13/52, which is the number of hearts in a full deck divided by the number of cards) times the probability of picking a heart on the second card (or 12/51, which is the number of hearts remaining in the deck divided by the number of cards remaining in the deck).
13/52 x 12/51 = 12/204
CASE 2: Similarly, the probability that the first card is a non-heart AND the second card is a heart is equal to the probability that the first card is NOT a heart (or 39/52) times the probability of subsequently picking a heart on the 2nd card (or 13/51). 39/52 x 13/51 = 39/204
Since these two cases are mutually exclusive, we can add them together to get the total probability of getting a heart as the second card: 12/204 + 39/204 = 51/204 = 1/4.
We can do a similar analysis for any card in the deck, and, although the probability tree gets more complicated as the card number gets higher, the total probability that the n th card dealt will be a heart will always end up simplifying to 1/4.
If the probability that Brendon, Daniel and Kane score more than or equal to 700 on the GMAT is 0.4, 0.5 and 0.6 respectively, what is the probability that at least 2 of them score less than 700?- a)0.12
- b)0.38
- c)0.40
- d)0.50
- e)0.60
Correct answer is option 'D'. Can you explain this answer?
If the probability that Brendon, Daniel and Kane score more than or equal to 700 on the GMAT is 0.4, 0.5 and 0.6 respectively, what is the probability that at least 2 of them score less than 700?
a)
0.12
b)
0.38
c)
0.40
d)
0.50
e)
0.60
|
|
Ameya Yadav answered |
Given
- P(Brendon scoring more than or equal to 700) = 0.4
- P(Daniel scoring more than or equal to 700) = 0.5
- P(Kane scoring more than or equal to 700) = 0.6
To Find: Probability that at-least 2 of them score less than 700?
Approach
- P(at-least 2 of them score less than 700) = P(exactly 2 of them score less than 700 or all 3 of them score less than 700)
- Event-1: Two of them score less than 700
- Event-2: All 3 of them score less than 700
- P(Event) = P(Event-1) + P(Event-2)
- Event-1: Two of them score less than 700
- The possible combinations can be:
- Case-I: Brendon and Daniel scoring less than 700 AND kane scoring more than or equal to 700 OR
- Case-II: Daniel and Kane scoring less than 700 AND Brendon scoring more than or equal to 700 OR
- Case-III: Kane and Brendon scoring less than 700 AND Daniel scoring more than or equal to 700
- P(Event-1) = P(case-I) + P(case-II) + P(case-III)
- The possible combinations can be:
- Event-2: All 3 of them scoring less than 700
- Event-2 = (Bredon scoring less than 700 AND Daniel scoring less than 700 AND Kane scoring less than 700)
- P(Event-2) = P(Brendon scoring less than 700) * P(Daniel scoring less than 700) *P(Kane scoring less than 700)
Working Out
- Event-1: Two of them scoring less than 700
- Case-I: (1-0.4) * (1- 0.5) * 0.6 = 0.18
- Case-II: 0.4 *(1-0.5) *(1-0.6) = 0.08
- Case-III: (1-0.4) * 0.5 * (1- 0.6) = 0.12
- P(Event-1) = 0.18 + 0.08 + 0.12 =0.38
- Event-2: All 3 of them scoring less than 700
- P(Event-2) = (1-0.4) * (1-0.5) * (1-0.6) = 0.6 * 0.5 * 0.4 = 0.12
- P(Event) = P(Event-1) + P(Event-2) = 0.38 + 0.12 = 0.50
What is the probability that a person born between the years 1990 and 2010, inclusive, was born in a leap year? - a)1/21
- b)1/7
- c)1/5
- d)5/21
- e)1/4
Correct answer is option 'D'. Can you explain this answer?
What is the probability that a person born between the years 1990 and 2010, inclusive, was born in a leap year?
a)
1/21
b)
1/7
c)
1/5
d)
5/21
e)
1/4
|
|
Amar Chakraborty answered |
Step I: Define Event
The event here is that the person was born in a leap year between 1990 and 2010, inclusive. We know that a leap year is a year that is divisible by 4.
Step II: Find n, the number of ways in which all outcomes can occur
Since the boundary years 1990 and 2010 are included as well, the total number of years to be considered is 2010 – 1990 + 1 = 21.
(Note: Suppose the years given were 1990-1992 inclusive, then how many years would that be? 3 years: 1990, 1991 and 1992. But 1992-1990 is equal to only 2. Therefore, when the boundary years are included, the correct formula to count the number of years will be: Final Year – Initial Year + 1)
The person may be born in any of these years.
Thus, n = 21C1 = 21
Step III: Find x, the number of ways in which the event can occur
To calculate x, we need to find the leap years between 1990 and 2010, inclusive.
We know that a number is divisible by 4 if its last two digits are divisible by 4. Using this rule, we can determine that the leap years will be:
1992, 1996, 2000, 2004 and 2008
Thus, there are 5 leap years. The person being born in any of these 5 years will be a favorable outcome.
Therefore, x = 5
Step IV: Calculate probability
P = x/n = 5/21
Answer: Option (D)
A, B, C, D, E, and F are six consecutive positive odd integers in increasing order. What is the value of the median of these six integers?(1) The sum of the two smallest integers is greater than the largest integer by 13 (2) The average (arithmetic mean) of these integers is 26- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'D'. Can you explain this answer?
A, B, C, D, E, and F are six consecutive positive odd integers in increasing order. What is the value of the median of these six integers?
(1) The sum of the two smallest integers is greater than the largest integer by 13
(2) The average (arithmetic mean) of these integers is 26
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.
|
|
Mihir Ghoshal answered |
Steps 1 & 2: Understand Question and Draw Inferences
We are given six consecutive positive odd integers. We have to find the median of this set of integers.
Since the integers are consecutive odd integers, they can be represented with the help of a positive integer n, as follows:
A = 2*n + 1
B = 2*n + 3
C = 2*n + 5
D = 2*n + 7
E = 2*n + 9
F = 2*n + 11
Now, we know that, for a series in increasing order, the median is the middle number in case of odd number of integers and the average of the middle two numbers in case of even number of integers.
Since there are even number (6) of integers in this series, the median will be the average of the 3rd and 4th number:
Thus, in order to find the value of the median, we need to know the value of n. So, the question becomes “what is the value of n?”
Step 3: Analyze Statement 1
The sum of the two smallest integers is greater than the largest integer by 13 ?
Now, the two smallest integers in the sequence are 2n+1 and 2n+3 and their sum = 4n+4
The largest integer in the sequence is 2n+11.
Per statement (1), the difference between these two should be 13. So,
(4n+4) – (2n+11) = 13
2n-7 = 13
2n = 20
Thus, n =10.
Now, since we have found the value of n, we can find the median.
Hence, statement (1) is sufficient to find a unique value of the median.
Step 4: Analyze Statement 2
The average (arithmetic mean) of these integers is 26
Thus:
Now, since we have found the value of n, we can find the median.
Hence, statement (2) is sufficient to find a unique value of the median
Step 5: Analyze Both Statements Together (if needed)
Since statement (1) and (2) alone are sufficient to answer the question, we don’t need to perform this step.
Answer: Option (D)
In a room filled with 7 people, 4 people have exactly 1 friend in the room and 3 people have exactly 2 friends in the room (Assuming that friendship is a mutual relationship, i.e. if John is Peter's friend, Peter is John's friend). If two individuals are selected from the room at random, what is the probability that those two individuals are NOT friends? - a)5/21
- b)3/7
- c)4/7
- d)5/7
- e)16/21
Correct answer is option 'E'. Can you explain this answer?
In a room filled with 7 people, 4 people have exactly 1 friend in the room and 3 people have exactly 2 friends in the room (Assuming that friendship is a mutual relationship, i.e. if John is Peter's friend, Peter is John's friend). If two individuals are selected from the room at random, what is the probability that those two individuals are NOT friends?
a)
5/21
b)
3/7
c)
4/7
d)
5/7
e)
16/21
|
|
Akshay Khanna answered |
Begin by counting the number of relationships that exist among the 7 individuals whom we will call A, B, C, D, E, F, and G.
First consider the relationships of individual A: AB, AC, AD, AE, AF, AG = 6 total. Then consider the relationships of individual B without counting the relationship AB that was already counted before: BC, BD, BE, BF, BG = 5 total. Continuing this pattern, we can see that C will add an additional 4 relationships, D will add an additional 3 relationships, E will add an additional 2 relationships, and F will add 1 additional relationship. Thus, there are a total of 6 + 5 + 4 + 3 + 2 + 1 = 21 total relationships between the 7 individuals.
Alternatively, this can be computed formulaically as choosing a group of 2 from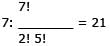
We are told that 4 people have exactly 1 friend. This would account for 2 "friendship" relationships (e.g. AB and CD). We are also told that 3 people have exactly 2 friends. This would account for another 3 "friendship" relationships (e.g. EF, EG, and FG). Thus, there are 5 total "friendship" relationships in the group.
The probability that any 2 individuals in the group are friends is 5/21. The probability that any 2 individuals in the group are NOT friends = 1 – 5/21 = 16/21.
First consider the relationships of individual A: AB, AC, AD, AE, AF, AG = 6 total. Then consider the relationships of individual B without counting the relationship AB that was already counted before: BC, BD, BE, BF, BG = 5 total. Continuing this pattern, we can see that C will add an additional 4 relationships, D will add an additional 3 relationships, E will add an additional 2 relationships, and F will add 1 additional relationship. Thus, there are a total of 6 + 5 + 4 + 3 + 2 + 1 = 21 total relationships between the 7 individuals.
Alternatively, this can be computed formulaically as choosing a group of 2 from
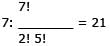
We are told that 4 people have exactly 1 friend. This would account for 2 "friendship" relationships (e.g. AB and CD). We are also told that 3 people have exactly 2 friends. This would account for another 3 "friendship" relationships (e.g. EF, EG, and FG). Thus, there are 5 total "friendship" relationships in the group.
The probability that any 2 individuals in the group are friends is 5/21. The probability that any 2 individuals in the group are NOT friends = 1 – 5/21 = 16/21.
Set X consists of 10 integers and has median of 20 and a range of 20. What is the value of the greatest possible integer that can be present in the set?- a)32
- b)37
- c)40
- d)43
- e)50
Correct answer is option 'C'. Can you explain this answer?
Set X consists of 10 integers and has median of 20 and a range of 20. What is the value of the greatest possible integer that can be present in the set?
a)
32
b)
37
c)
40
d)
43
e)
50
|
|
Sravya Joshi answered |
Given: Median and Range
To Find: The greatest possible number
Let the lowest number be P and the greatest number be Q
Given:
- Range = 20
- Q – P = 20
- Q = 20 + P
Here we expressed Q (the highest value) in terms of P (the lowest value).
Therefore by finding the max value of P, we can find the max value of Q.
Now we know that the median = 20
- So, the greatest value which P can take = 20
- This means that at least 6 numbers in the given set of 10 numbers will have the same value of 20. This ways, when the 10 numbers are arranged in an ascending order, the median will be equal to half the sum of the 5th and 6th term. And so, will be equal to 20. The 7th, 8th and 9th terms (when the 10 numbers are arranged in an ascending order) can take any value between 20 and 40. The 10th term will be 40.
- That is, Q = 40
- Thus, the greatest integer that can be present in this set is 40.
Remember -The difference between any two numbers in a set cannot be greater than the range.
Answer: Option (C)
While debugging a piece of software, an engineer records the number of bugs he finds each day. If the number of bugs found by the engineer reduces by x with each passing day, what is the standard deviation of the number of bugs found by the engineer during the last 7 days?
(1) The difference between the maximum number of bugs and the minimum number of bugs found by the engineer during the last 7
days is 24.
(2) The average (arithmetic mean) number of bugs found by the engineer during the last 7 days is 24- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked. - b)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked. - c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked. - d)EACH statement ALONE is sufficient to answer the question
asked. - e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
Correct answer is option 'A'. Can you explain this answer?
While debugging a piece of software, an engineer records the number of bugs he finds each day. If the number of bugs found by the engineer reduces by x with each passing day, what is the standard deviation of the number of bugs found by the engineer during the last 7 days?
(1) The difference between the maximum number of bugs and the minimum number of bugs found by the engineer during the last 7
days is 24.
(2) The average (arithmetic mean) number of bugs found by the engineer during the last 7 days is 24
(1) The difference between the maximum number of bugs and the minimum number of bugs found by the engineer during the last 7
days is 24.
(2) The average (arithmetic mean) number of bugs found by the engineer during the last 7 days is 24
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
answer the question asked, and additional data specific to the
problem are needed.
|
|
Malavika Choudhury answered |
The Problem Overview
The engineer records the daily number of bugs found over 7 days, with a consistent reduction of x bugs daily. We need to determine the standard deviation of these findings.
Statement Analysis
Statement (1): The difference between the maximum and minimum number of bugs found is 24.
- This indicates that the range of the bugs found is 24.
- Since the number of bugs decreases daily, the values can be represented as:
- Day 1: M (maximum)
- Day 2: M - x
- Day 3: M - 2x
- ...
- Day 7: M - 6x
- The minimum value (Day 7) can be expressed as M - 6x, leading to:
- M - (M - 6x) = 24
- Thus, 6x = 24, which gives x = 4.
- The specific values for each day can be calculated, allowing the standard deviation to be found.
- Hence, this statement alone is sufficient.
Statement (2): The average number of bugs found is 24.
- The average does not provide enough information about the distribution of the daily values.
- Without the daily values or their range, we cannot calculate the standard deviation.
- Therefore, this statement alone is not sufficient.
Conclusion
- Statement (1) provides enough information to calculate the standard deviation.
- Statement (2) does not provide sufficient data alone.
The correct answer is option 'A': Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
The engineer records the daily number of bugs found over 7 days, with a consistent reduction of x bugs daily. We need to determine the standard deviation of these findings.
Statement Analysis
Statement (1): The difference between the maximum and minimum number of bugs found is 24.
- This indicates that the range of the bugs found is 24.
- Since the number of bugs decreases daily, the values can be represented as:
- Day 1: M (maximum)
- Day 2: M - x
- Day 3: M - 2x
- ...
- Day 7: M - 6x
- The minimum value (Day 7) can be expressed as M - 6x, leading to:
- M - (M - 6x) = 24
- Thus, 6x = 24, which gives x = 4.
- The specific values for each day can be calculated, allowing the standard deviation to be found.
- Hence, this statement alone is sufficient.
Statement (2): The average number of bugs found is 24.
- The average does not provide enough information about the distribution of the daily values.
- Without the daily values or their range, we cannot calculate the standard deviation.
- Therefore, this statement alone is not sufficient.
Conclusion
- Statement (1) provides enough information to calculate the standard deviation.
- Statement (2) does not provide sufficient data alone.
The correct answer is option 'A': Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
Five children, Anaxagoras, Beatrice, Childeric, Desdemona, and Ethelred, sit randomly in five chairs in a row. What is the probability that Childeric and Ethelred sit next to each other?- a)1/30
- b)1/15
- c)1/5
- d)2/5
- e)7/20
Correct answer is option 'D'. Can you explain this answer?
Five children, Anaxagoras, Beatrice, Childeric, Desdemona, and Ethelred, sit randomly in five chairs in a row. What is the probability that Childeric and Ethelred sit next to each other?
a)
1/30
b)
1/15
c)
1/5
d)
2/5
e)
7/20
|
|
S.S Career Academy answered |
First, we will count all the possible arrangements of the five children on the five seats, all the possible orders. This is 5! = 120. That’s the denominator.
Now, the more challenging part: we have to figure out how many arrangements there are involving C & E sitting together. This is a tricky problem to frame, so I’ll demonstrate the steps to follow. First, let’s look at the seats these two could be next to each other. There are four possible pairs of seats in which they could be next to each other
i. X X _ _ _
ii. _ X X _ _
iii. _ _ X X _
iv. _ _ _ X X
In each of those four cases, we could have either CE or EC, either order, so that’s 4 x 2 = 8 ways we could have just C & E sitting next to each other with the remaining three seats empty.
For the final step, we need to consider the other three children, A & B & D. In each of the eight cases, there are three blank seats waiting for those three, and those three could be put in any order in those blank seats. Three elements in any order—that’s 3! = 6. Thus, the total number of arrangements in which C & E would be next to each other would be 8 x 6 = 48. This is our numerator.
The probability would be this number, 48, over the total number of arrangements of the children, 120.
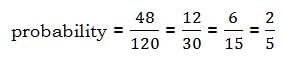
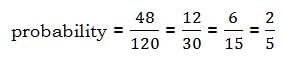
A small company employs 3 men and 5 women. If a team of 4 employees is to be randomly selected to organize the company retreat, what is the probability that the team will have exactly 2 women?- a)1/14
- b)1/7
- c)2/7
- d)3/7
- e)1/2
Correct answer is option 'D'. Can you explain this answer?
A small company employs 3 men and 5 women. If a team of 4 employees is to be randomly selected to organize the company retreat, what is the probability that the team will have exactly 2 women?
a)
1/14
b)
1/7
c)
2/7
d)
3/7
e)
1/2
|
|
Tejas Gupta answered |
First, we must calculate the total number of possible teams (let’s call this t ). Then, we must calculate how many of these possible teams have exactly 2 women (let’s call this w). The probability that a randomly selected team will have exactly 2 women can be expressed as w/t.
To calculate the number of possible teams, we can use the Anagram Grid method. Since there are 8 employees, 4 of whom will be on the team (represented with a Y) and 4 of whom will not (represented with an N), we can arrange the following anagram grid:
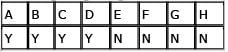
To make the calculation easier, we can use the following shortcut: t = (8!)/(4!)(4!). The (8!) in the numerator comes from the fact that there are 8 total employees to choose from. The first (4!) in the denominator comes from the fact that 4 employees will be on the team, and the other (4!) comes from the fact that 4 employees will not be on the team. Simplifying yields:
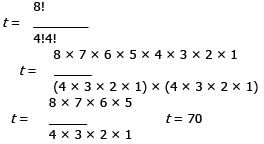
So, there are 70 possible teams of 4 employees. Next, we can use a similar method to determine w, the number of possible teams with exactly 2 women. We note that in order to have exactly 2 women on the team, there must also be 2 men on the team of 4. If we calculate the number of ways that 2 out of 5 women can be selected, and the number of ways that 2 out of 3 men can be selected, we can then multiply the two to get the total number of teams consisting of 2 men and 2 women. Let’s start with the women:
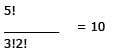
So, the number of ways that 2 women can be selected is 10. Now the men:
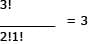
Thus, the number of ways that 2 men can be selected is 3. Now we can multiply to get the total number of 2 women teams: w = (10)(3) = 30. Since there are 30 possible teams with exactly 2 women, and 70 possible teams overall, w /t = 30/70 = 3/7.
To calculate the number of possible teams, we can use the Anagram Grid method. Since there are 8 employees, 4 of whom will be on the team (represented with a Y) and 4 of whom will not (represented with an N), we can arrange the following anagram grid:
To make the calculation easier, we can use the following shortcut: t = (8!)/(4!)(4!). The (8!) in the numerator comes from the fact that there are 8 total employees to choose from. The first (4!) in the denominator comes from the fact that 4 employees will be on the team, and the other (4!) comes from the fact that 4 employees will not be on the team. Simplifying yields:
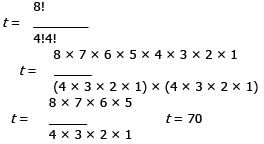
So, there are 70 possible teams of 4 employees. Next, we can use a similar method to determine w, the number of possible teams with exactly 2 women. We note that in order to have exactly 2 women on the team, there must also be 2 men on the team of 4. If we calculate the number of ways that 2 out of 5 women can be selected, and the number of ways that 2 out of 3 men can be selected, we can then multiply the two to get the total number of teams consisting of 2 men and 2 women. Let’s start with the women:
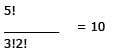
So, the number of ways that 2 women can be selected is 10. Now the men:
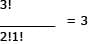
Thus, the number of ways that 2 men can be selected is 3. Now we can multiply to get the total number of 2 women teams: w = (10)(3) = 30. Since there are 30 possible teams with exactly 2 women, and 70 possible teams overall, w /t = 30/70 = 3/7.
List A: 20, 4, 8, x
List B: 8, 3, 6, 12, -4
List A above has 4 numbers and List B above has 5 numbers. What is the value of x?(1) The range of the numbers in List A is equal to the range of the numbers in List B(2) The median of the numbers in List A is equal to the median of the numbers in List B.- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked. - b)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked. - c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked. - d)EACH statement ALONE is sufficient to answer the question
asked. - e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'C'. Can you explain this answer?
List A: 20, 4, 8, x
List B: 8, 3, 6, 12, -4
List A above has 4 numbers and List B above has 5 numbers. What is the value of x?
List B: 8, 3, 6, 12, -4
List A above has 4 numbers and List B above has 5 numbers. What is the value of x?
(1) The range of the numbers in List A is equal to the range of the numbers in List B
(2) The median of the numbers in List A is equal to the median of the numbers in List B.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the problem are needed.
answer the question asked, and additional data specific to the problem are needed.
|
|
Rutuja Banerjee answered |
Step 1 & 2: Understand Question and Draw Inference
Given:
- List A: 4, 8, 20, x (don’t know the value of x, other numbers arranged in ascending order)
- List B: -4, 3, 6, 8, 12 (numbers arranged in ascending order)
To find: x = ?
Step 3 : Analyze Statement 1 independent
(1) The range of the numbers in List A is equal to the range of the numbers in List B
- Range of List B = 12 – (-4 ) = 12 + 4 = 16
- So, Range of List A = 16
- (Greatest number of List A) – (Smallest number of List A) = 16
- In List A, difference between 20 and 4 is 16
- This means, Greatest number of List A = 20
- And, Smallest number of List A = 4
- This means, 4 ≤ x ≤ 20
Not sufficient to find a unique value of x.
Step 4 : Analyze Statement 2 independent
(2) The median of the numbers in List A is equal to the median of the numbers
in List B.
in List B.
- Median of List B = 6
- So, Median of List A = 6
- In List A, possible arrangements of the 4 elements in ascending order and the corresponding medians:
- Thus, from Statement 2, we infer that x ≤ 4
Not sufficient to find a unique value of x
Step 5: Analyze Both Statements Together (if needed)
- From Statement 1: 4 ≤ x ≤ 20
- From Statement 2: x ≤ 4
- combing the 2 statements: x = 4Combin
Thus, the two statements together are sufficient to find a unique value of x
Answer: Option C
Answer: Option C
Three squares on a chessboard are chosen at random. The probability that 2 of them are of one color and the remaining one is of another color is: - a)3/64
- b)64/441
- c)5/21
- d)8/21
- e)16/21
Correct answer is option 'E'. Can you explain this answer?
Three squares on a chessboard are chosen at random. The probability that 2 of them are of one color and the remaining one is of another color is:
a)
3/64
b)
64/441
c)
5/21
d)
8/21
e)
16/21
|
|
Hridoy Desai answered |
A. Write Probability Event Equation
We are given that 3 squares on a chessboard are chosen at random. We have to find the probability that 2 of these squares are of one color and the remaining one is of another color.
A chessboard has 8 rows and 8 columns. So, there are total 8*8 = 64 squares on the chessboard. Out of these 64 squares, 32 are black and 32 are white.
So, the events in this case are:
Event 1: Selecting two black squares and one white square
Event 2: Selecting one black squares and two white square
Since the objective of the question can be completed by accomplishing either Event 1 OR Event 2, we will use an addition sign in the Probability Event Equation:
P(Selecting3squaresonachessboardundergivenconstraint)=P(Event1)+P(Event2)
B. Determine Probabilities of Individual Events
Event 1
Step I: Define Event
There are 64 squares on the chessboard, of which 32 are black and 32 are white.
Event 1 is to select 2 black squares and 1 white square.
Step II: Find n1, the number of ways in which all outcomes can occur
The total possible outcomes in this case is equal to the number of ways to select any 3 squares from the chessboard. So, the number of ways in which 3 squares can be selected from 64 squares
= 64C3
Thus, n1 = 64C3
Step III: Find x1, the number of ways in which the event can occur
To accomplish Event 1, we have to do the following tasks:
- Select 2 black squares
- Select one white square
The number of ways to select 2 black squares from 32 black squares = 32C2
The number of ways to select 1 white square from 32 white squares = 32C1
Since both these tasks need to be completed to accomplish the objective of Event 1, we will use a multiplication sign between the number of ways of doing the two events:
Thus, x1 = 32C2 * 32C1
Step IV: Calculate probability
NOTE: Order doesn't matter here - Hence, it is a Selection Question.
For Example:
Better Method (Combination): We will just select 2 black and 1 white square.
OR
Lengthy Method (Permutation): We consider all the following 3 cases:
1) We select first white and then 2 blacks OR
2) We select first 2 blacks and then white.
3) we select first a black, then white and then a black.
Event 2
Step I: Define Event
There are 64 squares on the chessboard, of which 32 are black and 32 are white.
Event 2 is to select 1 black square and 2 white squares.
Similar to Event 1, Order doesn't matter here.
Step II: Find n2, the number of ways in which all outcomes can occur
The total possible outcomes in this case is equal to the number of ways to select any 3 squares from the chessboard. So, the number of ways in which 3 squares can be selected from 64 squares
= 64C3
Thus, n2 = 64C3
Step III: Find x2, the number of ways in which the event can occur
To accomplish Event 2, we have to do the following tasks:
- Select 1 black square
- Select 2 white squares
The number of ways to select 1 black square from 32 black squares = 32C1
The number of ways to select 2 white squares from 32 white squares = 32C2
Since both these tasks need to be completed to accomplish the objective of Event 2, we will use a multiplication sign between the number of ways of doing the two events:
Step IV: Calculate probability
C. Plug the values in the Probability Event Equation
P(Selecting 3 squares on a chess board undergiven constraint) =P (Event1) +P (Event2)
Answer: Option (E)
A dance group consists of 6 men and 7 women. There are 3 married couples in the group. If 2 people have to be selected – 1 man and 1 woman, what is the probability that one of the couples will be selected?- a)1/14
- b)1/7
- c)1/6
- d)1/3
- e)1/2
Correct answer is option 'A'. Can you explain this answer?
A dance group consists of 6 men and 7 women. There are 3 married couples in the group. If 2 people have to be selected – 1 man and 1 woman, what is the probability that one of the couples will be selected?
a)
1/14
b)
1/7
c)
1/6
d)
1/3
e)
1/2
|
|
Gitanjali Kumar answered |
Step 1: Define the Event
Consider 6 men in the group to be M1 M2 M3 M4 M5 M6
Consider 7 women in the group to be W1 W2 W3 W4 W5 W6 W7
The group has 3 married couples.
(Consider (M1, W1) (M2, W2) and (M3, W3) to be the married couples.)
1 man out of the 6 men in the group &
1 woman out of the 7 women in the group are to be selected.
The Event is that one of the 3 married couples gets selected.
Step 2: Find n, the number of ways in which all outcomes can occur
- Total number of ways in which 1 man can be selected out of 6 men = 6C1 = 6
- Total number of ways in which 1 woman can be selected out of 7 women = 7C1 = 7
Thus,
- Total number of possible outcomes, n = 6 x 7 = 42
(For example, selections like: (M1, W7) (M2, W5) (M1, W1) ……........................... etc. are all possible)
Note here that we use a multiplication sign in the above equation because we need to select both a man AND a woman.
Step 3: Find x, the number of ways in which the event can occur
The Event is the selection of a married couple.
In how many ways you can select a married couple out of 3 married couples??
- No: of ways in which 1 married couple can be selected out of 3 married couples
- 3C1 = 3
Thus,
- x = 3
Step 4: Probability = x/n
Therefore,
- Probability (a married couple is selected) = x/n = 3/42 = 1/14
In other words,
Out of the 42 possible selections ((M1, W7) (M2, W5) (M1, W1) …................…. etc.),
there are 3 selections ((M1, W1) (M2, W2) and (M3, W3)) who will be married couples.
Correct Answer: Option A
Two letters from the word FARTHING are selected at random. What is the probability that at least one of the selected letters is a consonant?- a)1/500
- b)1/28
- c)27/28
- d)124/125
- e)499/500
Correct answer is option 'C'. Can you explain this answer?
Two letters from the word FARTHING are selected at random. What is the probability that at least one of the selected letters is a consonant?
a)
1/500
b)
1/28
c)
27/28
d)
124/125
e)
499/500
|
|
Maya Khanna answered |
To find the probability that at least one of the selected letters is a consonant, we can calculate the probability of the complement event (i.e., the event where both selected letters are vowels) and subtract it from 1.
Total number of ways to select two letters from the word FARTHING = 8C2 = 28
Total number of ways to select two vowels from the word FARTHING = 3C2 = 3
So, the probability of selecting two vowels is 3/28.
To find the probability of at least one consonant, we subtract the probability of selecting two vowels from 1:
P(at least one consonant) = 1 - P(two vowels)
= 1 - 3/28
= 25/28
Therefore, the probability that at least one of the selected letters is a consonant is 25/28.
Thus, the correct answer is option C) 27/28.
Total number of ways to select two letters from the word FARTHING = 8C2 = 28
Total number of ways to select two vowels from the word FARTHING = 3C2 = 3
So, the probability of selecting two vowels is 3/28.
To find the probability of at least one consonant, we subtract the probability of selecting two vowels from 1:
P(at least one consonant) = 1 - P(two vowels)
= 1 - 3/28
= 25/28
Therefore, the probability that at least one of the selected letters is a consonant is 25/28.
Thus, the correct answer is option C) 27/28.
Chapter doubts & questions for Probability & Statistics - Quantitative for GMAT 2025 is part of GMAT exam preparation. The chapters have been prepared according to the GMAT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for GMAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Probability & Statistics - Quantitative for GMAT in English & Hindi are available as part of GMAT exam.
Download more important topics, notes, lectures and mock test series for GMAT Exam by signing up for free.
Quantitative for GMAT
121 videos|148 docs|111 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup