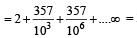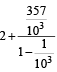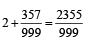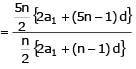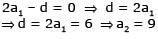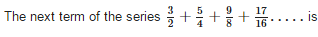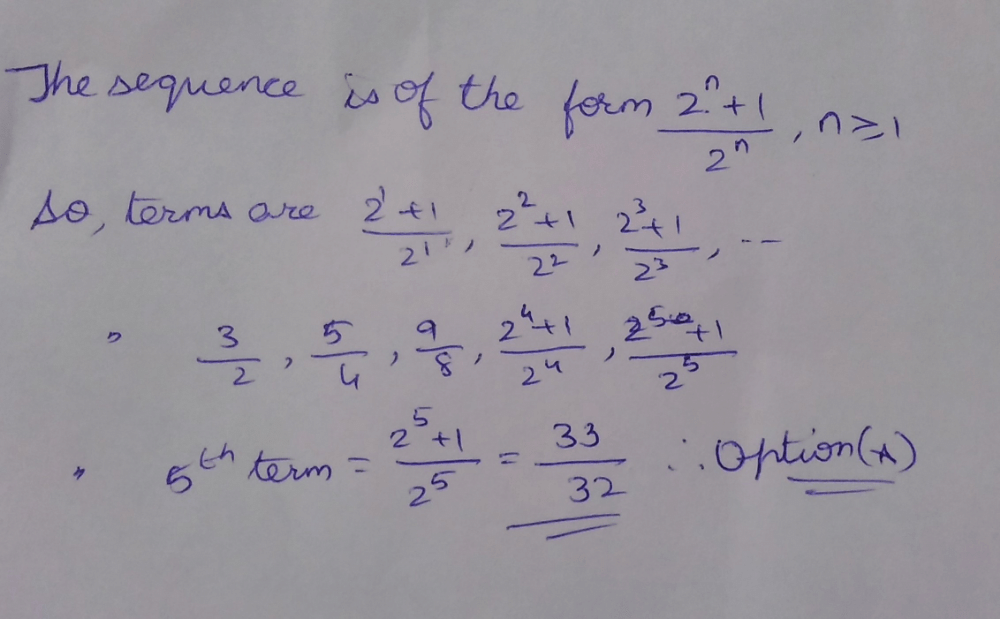All Exams >
JEE >
Chapter-wise Tests for JEE Main & Advanced >
All Questions
All questions of Sequences and Series for JEE Exam
What is the 50th term of the sequence √3, 3, 3√3, 9, ......- a)(√3)49
- b)(√3)50
- c)349
- d)350
Correct answer is option 'B'. Can you explain this answer?
What is the 50th term of the sequence √3, 3, 3√3, 9, ......
a)
(√3)49
b)
(√3)50
c)
349
d)
350
|
|
Nandini Iyer answered |
an = ar(n-1)
Given, a = √3, r = 3/√3
r = √3
a50 = ar(n-1)
= (√3)(√3)(50-1)
= (√3)(√3)49
= (√3)50
Given, a = √3, r = 3/√3
r = √3
a50 = ar(n-1)
= (√3)(√3)(50-1)
= (√3)(√3)49
= (√3)50
Find the missing number. 1, 4, 9, 16, 25, 36, 49, (....)- a)64
- b)54
- c)56
- d)81
Correct answer is option 'A'. Can you explain this answer?
Find the missing number. 1, 4, 9, 16, 25, 36, 49, (....)
a)
64
b)
54
c)
56
d)
81
|
|
Anjana Sharma answered |
The given number series as follow as 1^2, 2^2, 3^2, 4^2, 5^2, 6^2, 7^2, 8^2, ...
So the next number is 8^2 = 64.
The terms of an A.P. are doubled, then the resulting sequence is- a)An A.P. with common difference equal to the common difference of the original A.P
- b)An A.P. with common difference thrice the common difference of the original A.P.
- c)An A.P. with common difference double the common difference of the original A.P.
- d)An A.P. with common difference half the common difference of the original A.P.
Correct answer is option 'C'. Can you explain this answer?
The terms of an A.P. are doubled, then the resulting sequence is
a)
An A.P. with common difference equal to the common difference of the original A.P
b)
An A.P. with common difference thrice the common difference of the original A.P.
c)
An A.P. with common difference double the common difference of the original A.P.
d)
An A.P. with common difference half the common difference of the original A.P.
|
|
Lavanya Menon answered |
The general form of an AP is a, a+d, a+2d,.....
where a is the first term and d is the common difference
If we double the terms, the new sequence would be
A , a+2d, a+4d,......
We can observe that this sequence is also an AP
First term is a
Common difference is 2d nth term= 2a+(n-1)2d
= 2[a+(n-1)d]
where a is the first term and d is the common difference
If we double the terms, the new sequence would be
A , a+2d, a+4d,......
We can observe that this sequence is also an AP
First term is a
Common difference is 2d nth term= 2a+(n-1)2d
= 2[a+(n-1)d]
The next term of the sequence 1, 2, 4, 7,11,…. Is- a)18
- b)17
- c)16
- d)15
Correct answer is option 'C'. Can you explain this answer?
The next term of the sequence 1, 2, 4, 7,11,…. Is
a)
18
b)
17
c)
16
d)
15

|
Imk Pathsala answered |
The given series is: 1,2,4,7,11,...
Difference between second and first term = 2 - 1 = 1
Difference between third and second term = 4 - 2 = 2
Difference between fourth and third term = 7 - 4 = 3
Difference between fifth and fourth term = 11 - 7 = 4
Difference between sixth and fifth term = 16 - 11 = 5
Difference between second and first term = 2 - 1 = 1
Difference between third and second term = 4 - 2 = 2
Difference between fourth and third term = 7 - 4 = 3
Difference between fifth and fourth term = 11 - 7 = 4
Difference between sixth and fifth term = 16 - 11 = 5
The sum of the first hundred even natural numbers divisible by 5 is- a)55005
- b)55000
- c)50000
- d)50500
Correct answer is option 'D'. Can you explain this answer?
The sum of the first hundred even natural numbers divisible by 5 is
a)
55005
b)
55000
c)
50000
d)
50500
|
|
Preeti Iyer answered |
first even no. divisible by 5= 10
d=10
Sn = n/2(2a + (n-1) d)
S100= 100/2 (2(10) + (100-1)10)
S100=50(20 + 990)
S100= 50(1010)
S100 = 50500
Let a1, a2, a3, ....., a11 be real numbers satisfyinga1 = 15, 27 – 2a2 > 0 and ak = 2ak-1 – ak-2 for k = 3, 4, ...., 11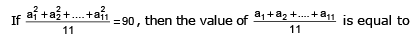 [JEE 2010]
[JEE 2010]- a)1
- b)0
- c)-1
- d)2
Correct answer is option 'B'. Can you explain this answer?
Let a1, a2, a3, ....., a11 be real numbers satisfying
a1 = 15, 27 – 2a2 > 0 and ak = 2ak-1 – ak-2 for k = 3, 4, ...., 11
[JEE 2010]
a)
1
b)
0
c)
-1
d)
2
|
|
Ishan Choudhury answered |
= ak = 2ak-1 - ak-2
⇒ a1, a2, a3 ...., a11 are in A.P. with common difference d.
a1 = 15,a2 = 15+d, a3 = 15+2d ..... a11 = 15+ 10d
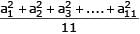
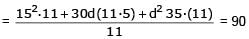
⇒ 35d2 + 150d + 225 = 90
⇒ 35d2 + 150d + 135 = 0
⇒ 7d2 + 30d + 27 = 0
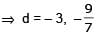
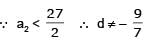
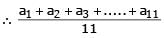
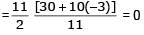
⇒ a1, a2, a3 ...., a11 are in A.P. with common difference d.
a1 = 15,a2 = 15+d, a3 = 15+2d ..... a11 = 15+ 10d
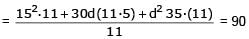
⇒ 35d2 + 150d + 225 = 90
⇒ 35d2 + 150d + 135 = 0
⇒ 7d2 + 30d + 27 = 0
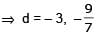
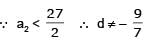
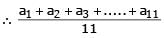
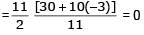
The first negative term of the A.P.62,57,52…. is the- a)10th term
- b)14th term
- c)12th term
- d)18th term
Correct answer is option 'B'. Can you explain this answer?
The first negative term of the A.P.62,57,52…. is the
a)
10th term
b)
14th term
c)
12th term
d)
18th term
|
|
Naina Sharma answered |
a = 62 d = 57 - 62 = -5
tn = a + (n-1)d
= 62 + (n-1)(-5)
= 62 - 5n + 5
= 67 - 5n
From the options, we take '14'
= 67 - 5(14)
= 67 - 70
= -3 (The first negative term will be at the 14th term)
tn = a + (n-1)d
= 62 + (n-1)(-5)
= 62 - 5n + 5
= 67 - 5n
From the options, we take '14'
= 67 - 5(14)
= 67 - 70
= -3 (The first negative term will be at the 14th term)
The three numbers between 1 and 256 such that the sequence is in GP are- a)4,16,64
- b)2,8,32
- c)8,16,32
- d)8,16,64
Correct answer is option 'A'. Can you explain this answer?
The three numbers between 1 and 256 such that the sequence is in GP are
a)
4,16,64
b)
2,8,32
c)
8,16,32
d)
8,16,64
|
|
Pooja Shah answered |
nth G.M. between a and b is
Gn = arn
Where common ratio is r = (b/a)(1/(n+1))
So, to insert 3 geometric means between 1 and 256
r = (b/a)(1/(n+1))
r = (256/(1)(1/(3+1))
r = (256)1/4
r = (4)(4)1/4
r = 4
Gn = 1 * (4)n
G1 = 1 * (4)1 = 4
G2 = 1 * (4)2 = 16
G3 = 1 * (4)3 = 64
The terms are 4, 16, 64
Gn = arn
Where common ratio is r = (b/a)(1/(n+1))
So, to insert 3 geometric means between 1 and 256
r = (b/a)(1/(n+1))
r = (256/(1)(1/(3+1))
r = (256)1/4
r = (4)(4)1/4
r = 4
Gn = 1 * (4)n
G1 = 1 * (4)1 = 4
G2 = 1 * (4)2 = 16
G3 = 1 * (4)3 = 64
The terms are 4, 16, 64
How many terms of the series
24,20,16,…are required so that their sum is 72?- a)8 or 6
- b)12
- c)9 or 4
- d)11
Correct answer is option 'C'. Can you explain this answer?
How many terms of the series
24,20,16,…are required so that their sum is 72?
24,20,16,…are required so that their sum is 72?
a)
8 or 6
b)
12
c)
9 or 4
d)
11
|
|
Naina Bansal answered |
As given above we can clearly see that the given series forms an AP. So we can use the sum formula to calculate it.
= Sn = n / 2 [ 2a + ( n-1 ) d ]
So the values are :
a = 24
d = -4
n = ?
Sn = 72
So substitute in the formula to get the answer:
= 72 = n / 2 [ 2 ( 24 ) + ( n - 1 ) -4 ]
= 72 = n / 2 [ 48 - 4n + 4 ]
= 72 * 2 = n [ 52 - 4n ]
= 144 = 52n - 4n^2
= 4n^2 - 52n + 144 = 0 ------ Dividing by 4 throughout the equation we get,
= n^2 - 13n + 36
Factorizing the above quadratic equation we get,
= n^2 - 9n - 4n + 36 = 0
= n ( n - 9 ) -4 ( n - 9 ) = 0
= ( n - 4 ) ( n - 9 ) = 0
= n = 4 , 9
So the number of terms can be both 4 terms and 9 terms. This is because since the AP is decreasing.
Hope it helps !!
The 5th term of the sequence 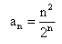 is
is- a)1
- b)5/16
- c)25/16
- d)25/32
Correct answer is option 'D'. Can you explain this answer?
The 5th term of the sequence 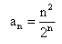 is
is
a)
1
b)
5/16
c)
25/16
d)
25/32
|
|
Riya Banerjee answered |
an = (n2)/2n
⇒ a5 = [(5)2]/2(5)
⇒ a5 = 25/32
⇒ a5 = [(5)2]/2(5)
⇒ a5 = 25/32
What is the 10th term of the sequence defined by an = (n-1)(2-n)(3+n)?
a) 792
b) -936
c) -924
d) -792
The answer is b.
|
|
Naina Sharma answered |
an = (n-1)(2-n)(3+n)
Put n = 10
an = 9×(-8)×13
= - 936
Put n = 10
an = 9×(-8)×13
= - 936
Sum of infinite number of terms of GP is 20 and sum of their square is 100. The common ratio of GP is [2002]- a)5
- b)3/5
- c)8/5
- d)1/5
Correct answer is option 'B'. Can you explain this answer?
Sum of infinite number of terms of GP is 20 and sum of their square is 100. The common ratio of GP is [2002]
a)
5
b)
3/5
c)
8/5
d)
1/5
|
|
Krishna Iyer answered |
Let a = first term of G.P. and r = common ratio of G.P.; Then G.P. is a, ar, ar2
Given 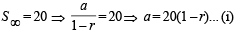
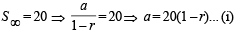
Also 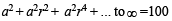
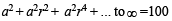
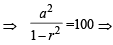 a2 = 100(1 – r)(1 + r)... (ii)
a2 = 100(1 – r)(1 + r)... (ii)From (i), a2 = 400(1 – r)2;
From (ii), we get 100(1 – r)(1 + r) = 400(1 – r)2
⇒ 1 + r = 4 – 4r
⇒ 5r = 3 ⇒ r = 3/5.
Three terms in A.P. are such that their sum is 45. What is the middle term?- a)25
- b)30
- c)15
- d)10
Correct answer is option 'C'. Can you explain this answer?
Three terms in A.P. are such that their sum is 45. What is the middle term?
a)
25
b)
30
c)
15
d)
10
|
|
Pooja Shah answered |
Let the three numbers be a-d, a, a+d
ATQ,
a - d + a + a + 2d = 45
3a = 45
a = 15
Middle term is 15
ATQ,
a - d + a + a + 2d = 45
3a = 45
a = 15
Middle term is 15
A man saved Rs 21700 in 14 years. In each year after the first he saved Rs 100 more than he did in the preceding year. How much did he save in the first year?- a)Rs 2100
- b)Rs 1300
- c)Rs 900
- d)Rs 600
Correct answer is option 'C'. Can you explain this answer?
A man saved Rs 21700 in 14 years. In each year after the first he saved Rs 100 more than he did in the preceding year. How much did he save in the first year?
a)
Rs 2100
b)
Rs 1300
c)
Rs 900
d)
Rs 600
|
|
Gaurav Kumar answered |
d = 100
Sn = 21700
n = 14
Sn = n/2[2a + (n-1)d]
21700 = 14/2[2a + (14-1)100]
= 21700 = 7[2a + 1300]
= 3100 = 2a + 1300
⇒ 3100 - 1300 = 2a
⇒ 1800 = 2a
⇒ a = 900
Sn = 21700
n = 14
Sn = n/2[2a + (n-1)d]
21700 = 14/2[2a + (14-1)100]
= 21700 = 7[2a + 1300]
= 3100 = 2a + 1300
⇒ 3100 - 1300 = 2a
⇒ 1800 = 2a
⇒ a = 900
If ar > 0, r ∈ N and a1, a2 , a3 , .............a2n are A.P. then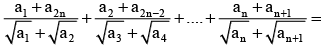
- a)n – 1
- b)
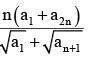
- c)
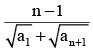
- d)n + 1
Correct answer is option 'B'. Can you explain this answer?
If ar > 0, r ∈ N and a1, a2 , a3 , .............a2n are A.P. then
a)
n – 1
b)
c)
d)
n + 1
|
|
Geetika Shah answered |
a1 + a2n = a2 + a2n-1 = an + an-1 = K(say)
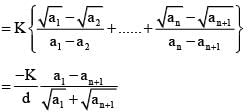
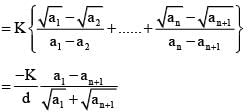
If a, b, c, d are in H.P., then ab + bc + cd is- a)3 b d
- b)(a + b) (c + d)
- c)3 a d
- d)3 a c
Correct answer is option 'C'. Can you explain this answer?
If a, b, c, d are in H.P., then ab + bc + cd is
a)
3 b d
b)
(a + b) (c + d)
c)
3 a d
d)
3 a c
|
|
Rajesh Gupta answered |
Since a,b,c are in H.P, so b = 2ac/(a+c).
Also, b,c,d are in H.P, so c = 2bd/(b+d).
Therefore, (a+c)(b+d) = 2ac/b × 2bd/c
⇒ab+cb+ad+cd = 4ad
⇒ab+bc+cd = 3ad
Also, b,c,d are in H.P, so c = 2bd/(b+d).
Therefore, (a+c)(b+d) = 2ac/b × 2bd/c
⇒ab+cb+ad+cd = 4ad
⇒ab+bc+cd = 3ad
If A1, A2, A3,…., An are n numbers between a and b, such that a, A1, A2, A3,…, An, b are in A.P., then nth term from beginning is:- a)b
- b)An-1
- c)An
- d)A1
Correct answer is option 'B'. Can you explain this answer?
If A1, A2, A3,…., An are n numbers between a and b, such that a, A1, A2, A3,…, An, b are in A.P., then nth term from beginning is:
a)
b
b)
An-1
c)
An
d)
A1
|
|
Krishna Iyer answered |
A1,A2,......, An are inserted between a and b then the series will become
a, A1,A2,A3,......, An,b. Now a becomes the first term, A1 will be second, A2 will become third term
An will become A(n+1)th term
therefore A(n-1) will become nth term.
a, A1,A2,A3,......, An,b. Now a becomes the first term, A1 will be second, A2 will become third term
An will become A(n+1)th term
therefore A(n-1) will become nth term.
The digits of a positive integer having three digits are in AP and sum of their digits is 21. The number obtained by reversing the digits is 396 less than the original number. Find the original number.- a)876
- b)579
- c)975
- d)678
Correct answer is option 'C'. Can you explain this answer?
The digits of a positive integer having three digits are in AP and sum of their digits is 21. The number obtained by reversing the digits is 396 less than the original number. Find the original number.
a)
876
b)
579
c)
975
d)
678

|
Trisha Vashisht answered |
Let the digits at ones, tens and hundreds place be (a−d)a and (a+d) respectively. The, the number is
(a+d)×100+a×10+(a−d) = 111a+99d
The number obtained by reversing the digits is
(a−d)×+a×10+(a+d) = 111a−99d
It is given that the sum of the digits is 21.
(a−d)+a+(a+d) = 21 ...(i)
Also it is given that the number obtained by reversing the digits is 594 less than the original number.
∴111a−99d = 111a+99d−396 ...(ii)
⟹ 3a = 21 and 198d = 396
⟹ a = 7 and d = -2
Original number = (a−d)×+a×10+(a+d)
= 100(9) + 10(7) + 5
= 975
(a+d)×100+a×10+(a−d) = 111a+99d
The number obtained by reversing the digits is
(a−d)×+a×10+(a+d) = 111a−99d
It is given that the sum of the digits is 21.
(a−d)+a+(a+d) = 21 ...(i)
Also it is given that the number obtained by reversing the digits is 594 less than the original number.
∴111a−99d = 111a+99d−396 ...(ii)
⟹ 3a = 21 and 198d = 396
⟹ a = 7 and d = -2
Original number = (a−d)×+a×10+(a+d)
= 100(9) + 10(7) + 5
= 975
The first 4 terms of the sequence 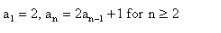 are
are- a)2, 6, 13, 27
- b)2, 5, 11, 23
- c)2, 6, 11, 24
- d)2, 5, 12, 37
Correct answer is option 'B'. Can you explain this answer?
The first 4 terms of the sequence 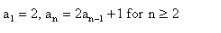 are
are
a)
2, 6, 13, 27
b)
2, 5, 11, 23
c)
2, 6, 11, 24
d)
2, 5, 12, 37
|
|
Geetika Shah answered |
a1 = 2
a2 = 2a1 + 1
=> 2(2) + 1 = 5
a3 = 2a2 + 1
=> 2(5) + 1 = 11
a4 = 2a3 + 1
=> 2(11) + 1 = 23
Hence, the required series is : 2,5,11,23………
a2 = 2a1 + 1
=> 2(2) + 1 = 5
a3 = 2a2 + 1
=> 2(5) + 1 = 11
a4 = 2a3 + 1
=> 2(11) + 1 = 23
Hence, the required series is : 2,5,11,23………
If 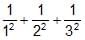 + ...... upto ¥ =
+ ...... upto ¥ =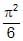 ,then
,then 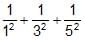 + ..... =
+ ..... =- a) p2/12
- b) p2/24
- c)p2/8
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
If 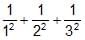 + ...... upto ¥ =
+ ...... upto ¥ =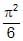 ,
,
then 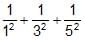 + ..... =
+ ..... =
a)
p2/12
b)
p2/24
c)
p2/8
d)
None of these

|
Sushil Kumar answered |
(1/12 + 1/22 + 1/32 + ........∞) = π2/6
⇒ (1/12 + 1/32 + 1/52 + ........∞) + (1/22 + 1/42 + 1/62 + ........∞) = π2/6
=> (1/12 + 1/32 + 1/52 + ........∞) + 1/22(1/12 + 1/22 + 1/32 + ........∞) = π2/6
=> (1/12 + 1/32 + 1/52 + ........∞) + 1/22(π2/6) = π2/6
=> (1/12 + 1/32 + 1/52 + ........∞) + π2/24 = π2/6
= π2/8
⇒ (1/12 + 1/32 + 1/52 + ........∞) + (1/22 + 1/42 + 1/62 + ........∞) = π2/6
=> (1/12 + 1/32 + 1/52 + ........∞) + 1/22(1/12 + 1/22 + 1/32 + ........∞) = π2/6
=> (1/12 + 1/32 + 1/52 + ........∞) + 1/22(π2/6) = π2/6
=> (1/12 + 1/32 + 1/52 + ........∞) + π2/24 = π2/6
= π2/8
Sum to 20 terms of the series (1.3)2 + (2.5)2 + (3.7)2 +… is:
- a)168090
- b)198090
- c)178090
- d)188090
Correct answer is option 'D'. Can you explain this answer?
Sum to 20 terms of the series (1.3)2 + (2.5)2 + (3.7)2 +… is:
a)
168090
b)
198090
c)
178090
d)
188090
|
|
Mira Joshi answered |
Given that (1.3)2, (2.5)2 , (3.7)2 .....................20 terms
Here 1,2,3,.................are in A.P.
a = 1, d = 1
tn = a + (n-1) d = 1 + (n -1)1 = n
3,5,7 ............. are in A.P
a = 3, d = 2
tn = a + (n-1) d = 3 + (n -1)2 = 2n + 1
∴ nth term = n(2n + 1)2 = 4n3 + 4n2 + n
Sum of n terms Sn = ∑ ( 4n3 + 4n2 + n ) = 4 { n2(n+1)2}/4 + 4 {n (n+1)(2n+1)} / 6 + n(n+1)/2
= { n2(n+1)2} + 2 {n (n+1)(2n+1)} / 3 + n(n+1)/2
Sum of 20 terms S20 = 400 × 441 + 40 × 41 × 7 + 10 ×21 = 176400 + 11480 + 210
= 188090.
Here 1,2,3,.................are in A.P.
a = 1, d = 1
tn = a + (n-1) d = 1 + (n -1)1 = n
3,5,7 ............. are in A.P
a = 3, d = 2
tn = a + (n-1) d = 3 + (n -1)2 = 2n + 1
∴ nth term = n(2n + 1)2 = 4n3 + 4n2 + n
Sum of n terms Sn = ∑ ( 4n3 + 4n2 + n ) = 4 { n2(n+1)2}/4 + 4 {n (n+1)(2n+1)} / 6 + n(n+1)/2
= { n2(n+1)2} + 2 {n (n+1)(2n+1)} / 3 + n(n+1)/2
Sum of 20 terms S20 = 400 × 441 + 40 × 41 × 7 + 10 ×21 = 176400 + 11480 + 210
= 188090.
In an A.P., sum of first p terms is equal to the sum of first q terms. Sum of its first p + q terms is- a)0
- b)- ( p + q)
- c)p + q
- d)none of these.
Correct answer is option 'A'. Can you explain this answer?
In an A.P., sum of first p terms is equal to the sum of first q terms. Sum of its first p + q terms is
a)
0
b)
- ( p + q)
c)
p + q
d)
none of these.

|
Trisha Vashisht answered |
Sp = Sq
⇒ p/2(2a+(p−1)d) = q/2(2a+(q−1)d)
⇒ p(2a+(p−1)d) = q(2a+(q−1)d)
⇒ 2ap + p2d − pd = 2aq + q2d − qd
⇒ 2a(p−q) + (p+q)(p−q)d − d(p−q) = 0
⇒ (p−q)[2a + (p+q)d − d] = 0
⇒ 2a + (p+q)d − d = 0
⇒ 2a + ((p+q) − 1)d = 0
⇒ Sp+q = 0
⇒ p/2(2a+(p−1)d) = q/2(2a+(q−1)d)
⇒ p(2a+(p−1)d) = q(2a+(q−1)d)
⇒ 2ap + p2d − pd = 2aq + q2d − qd
⇒ 2a(p−q) + (p+q)(p−q)d − d(p−q) = 0
⇒ (p−q)[2a + (p+q)d − d] = 0
⇒ 2a + (p+q)d − d = 0
⇒ 2a + ((p+q) − 1)d = 0
⇒ Sp+q = 0
If a, b, c are in A.P. and k is any non zero numbre, then ka , kb ,kc are in- a)A.P
- b)G.P
- c)H.P
- d)A.G.P.
Correct answer is option 'B'. Can you explain this answer?
If a, b, c are in A.P. and k is any non zero numbre, then ka , kb ,kc are in
a)
A.P
b)
G.P
c)
H.P
d)
A.G.P.

|
Mohit Rajpoot answered |
a, b, c are in AP
Let d be the common difference.
b = a + d,
c = a + 2d
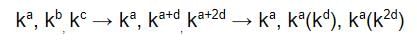
There are in GP with common ratio: kd
Let d be the common difference.
b = a + d,
c = a + 2d
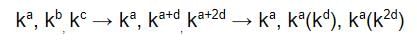
There are in GP with common ratio: kd
The arithmetic mean between 6 and – 12 is:- a)6
- b)-3
- c)-6
- d)9
Correct answer is option 'B'. Can you explain this answer?
The arithmetic mean between 6 and – 12 is:
a)
6
b)
-3
c)
-6
d)
9
|
|
Geetika Shah answered |
6, x, -12
x = (6-12)/2
x = -6/2
x = -3
x = (6-12)/2
x = -6/2
x = -3
Which term of the sequence 8 – 6i, 7 – 4i, 6 – 2i, ….is a real number ?- a)7th
- b)6th
- c)5th
- d)4th
Correct answer is option 'D'. Can you explain this answer?
Which term of the sequence 8 – 6i, 7 – 4i, 6 – 2i, ….is a real number ?
a)
7th
b)
6th
c)
5th
d)
4th
|
|
Preeti Iyer answered |
a = 8−6i
d = 7−4i−8+6i
= −1+2i
an = a+(n−1)d
a+ib = 8−6i+(n−1)(−1+2i)
a+ib = 8−6i+(−1)(n−1)+(n−1)2i
= − 6+2(n−1)=0
= 2(n−1) = 6
n = 4
an = 8−6i+(4−1)(−1+2i)
= 8−6i−3+6i = 5
4th term = 5
d = 7−4i−8+6i
= −1+2i
an = a+(n−1)d
a+ib = 8−6i+(n−1)(−1+2i)
a+ib = 8−6i+(−1)(n−1)+(n−1)2i
= − 6+2(n−1)=0
= 2(n−1) = 6
n = 4
an = 8−6i+(4−1)(−1+2i)
= 8−6i−3+6i = 5
4th term = 5
The next term of the sequence 1, 5, 14, 30, 55, …… is
- a)95
- b)91
- c)90
- d)80
Correct answer is option 'B'. Can you explain this answer?
The next term of the sequence 1, 5, 14, 30, 55, …… is
a)
95
b)
91
c)
90
d)
80
|
|
Mihir Chaudhary answered |
The sequence is obtained by adding consecutive odd numbers, starting with 1.
1 + 0 = 1
1 + 3 = 4
4 + 5 = 9
9 + 7 = 16
16 + 9 = 25
So the next term in the sequence is 25.
Therefore, the complete sequence is:
1, 5, 14, 30, 55, 25
1 + 0 = 1
1 + 3 = 4
4 + 5 = 9
9 + 7 = 16
16 + 9 = 25
So the next term in the sequence is 25.
Therefore, the complete sequence is:
1, 5, 14, 30, 55, 25
The A.M. between two numbers is 34 and their G.M. is 16.The numbers are- a)32 and 8
- b)64 and 4
- c)62 and 6
- d)60 and 18
Correct answer is option 'B'. Can you explain this answer?
The A.M. between two numbers is 34 and their G.M. is 16.The numbers are
a)
32 and 8
b)
64 and 4
c)
62 and 6
d)
60 and 18

|
Sushil Kumar answered |
Let the numbers be x, y
Then arithmatic mean = (x+y)/2 =34
→x+y =68
Also geometric mean =√(xy)=16
oy xy=16^2=256
Hence
x(68−x)=256
or x^2−68x+256=0
(x−64)(x−4)=0
Hence x=64 or x=4
and y=4 or 64
Larger number is 64
The value of 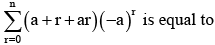
- a)
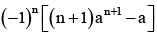
- b)
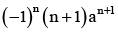
- c)
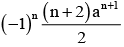
- d)
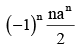
Correct answer is option 'B'. Can you explain this answer?
The value of 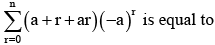
a)
b)
c)
d)

|
Sai Kulkarni answered |
= r(-a)r + a(r+1) (-a)r
= r(-a)r - (r+1) (-a)(r+1)
Tr = Vr - Vr+1
T1 = V1 - V2
T2 = V2 - V3
T3 = V3 - V4
.
.
.
.
.
Tn = Vn - V(n+1)
S = (r = 1 to n) Tr = V0 - V(n+1)
= (-1)n (n+1)(-a)(n+1)
= r(-a)r - (r+1) (-a)(r+1)
Tr = Vr - Vr+1
T1 = V1 - V2
T2 = V2 - V3
T3 = V3 - V4
.
.
.
.
.
Tn = Vn - V(n+1)
S = (r = 1 to n) Tr = V0 - V(n+1)
= (-1)n (n+1)(-a)(n+1)
The natural numbers are divided into groups 1, (2, 3), (4, 5, 6), (7, 8, 9, 10)....; then the sum of the numbers in the 50th group is- a)62500
- b)62520
- c)62525
- d)65225
Correct answer is option 'C'. Can you explain this answer?
The natural numbers are divided into groups 1, (2, 3), (4, 5, 6), (7, 8, 9, 10)....; then the sum of the numbers in the 50th group is
a)
62500
b)
62520
c)
62525
d)
65225
|
|
Pj Commerce Academy answered |
1
2 3
4 5 6
7 8 9 10
..........
Series for starting number:
1, 2, 4, 7, ...
Let Tn = an2 + bn + c
a+b+c=1 ......(1)
4a+2b+c=2 ......(2)
9a+3b+c=4 .......(3)
From eq (1), (2), (3), we get:
a= 1/2, b= −1/2, c=1
∴ Tn = n2/2 − n/2 + 1
∴ T50 = (50)2/2 − 50/2 + 1 = 1226
Now, elements in 50th group:
1226, 1227, 1228,.....(50 terms)
∴ Sn = 50/2[2×1226+(50−1)×1]
= 62525
2 3
4 5 6
7 8 9 10
..........
Series for starting number:
1, 2, 4, 7, ...
Let Tn = an2 + bn + c
a+b+c=1 ......(1)
4a+2b+c=2 ......(2)
9a+3b+c=4 .......(3)
From eq (1), (2), (3), we get:
a= 1/2, b= −1/2, c=1
∴ Tn = n2/2 − n/2 + 1
∴ T50 = (50)2/2 − 50/2 + 1 = 1226
Now, elements in 50th group:
1226, 1227, 1228,.....(50 terms)
∴ Sn = 50/2[2×1226+(50−1)×1]
= 62525
What is the 10th A.M between 2 and 57 if 10 A.M s are inserted between these numbers?
- a)54
- b)53
- c)52
- d)55
Correct answer is option 'C'. Can you explain this answer?
What is the 10th A.M between 2 and 57 if 10 A.M s are inserted between these numbers?
a)
54
b)
53
c)
52
d)
55
|
|
Aryan Khanna answered |
2 and 57 have 10 terms between them so including them there would be 12 terms
an = 57, a = 2, n = 12
an = a + (n-1)d
=> 57 = 2 + (12 - 1)d
=> 55 = 11d
d = 5
T10 = a + 10d
=> 2 + 10(5)
= 52
an = 57, a = 2, n = 12
an = a + (n-1)d
=> 57 = 2 + (12 - 1)d
=> 55 = 11d
d = 5
T10 = a + 10d
=> 2 + 10(5)
= 52
If we want to insert 8 numbers between the numbers 4 and 31 such that the resulting sequence is an AP.The difference between the consecutive numbers will be- a)4
- b)3
- c)2
- d)5
Correct answer is option 'B'. Can you explain this answer?
If we want to insert 8 numbers between the numbers 4 and 31 such that the resulting sequence is an AP.The difference between the consecutive numbers will be
a)
4
b)
3
c)
2
d)
5

|
New Words answered |
a = 4, l = 31, n = 8
(l-a)/(n+1) = (31-4)/(8+1)
= 27/9
= 3
(l-a)/(n+1) = (31-4)/(8+1)
= 27/9
= 3
If the sums of n, 2n and 3n terms of an AP are S1, S2 and S3 respectively, then 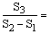
- a)
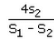
- b)
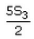
- c)3
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
If the sums of n, 2n and 3n terms of an AP are S1, S2 and S3 respectively, then
a)
b)
c)
3
d)
none of these
|
|
Pooja Shah answered |
Given x 2 - 3x = 0
Factor x out in the expression on the left.
x (x - 3) = 0
For the product x (x - 3) to be equal to zero we nedd to have
x = 0 or x - 3 = 0
Solve the above simple equations to obtain the solutions.
x = 0
or
x = 3
Factor x out in the expression on the left.
x (x - 3) = 0
For the product x (x - 3) to be equal to zero we nedd to have
x = 0 or x - 3 = 0
Solve the above simple equations to obtain the solutions.
x = 0
or
x = 3
The sum of the series 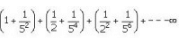
- a)49/25
- b)49/24
- c)47/24
- d)49/29
Correct answer is option 'B'. Can you explain this answer?
The sum of the series 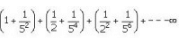
a)
49/25
b)
49/24
c)
47/24
d)
49/29

|
Knowledge Hub answered |
(1 + 1/52) + (1/2 + 1/52) + (1/22 + 1/54)+......
= (1 + 1/2 + 1/22 +....) + (1/52 + 1/54 + 1/56 +......)
= r = (1/4)/(1/2) , r = (1/54)/(1/52)
⇒ r = 1/2 + 1/25
⇒ S = 1 + [(1/2)/(1-1/2)], S = [(1/25)/(1-1/25)]
⇒ S = 1 + 1, S = 1/24
Total sum = 2 + 1/24
⇒ 49/24
= (1 + 1/2 + 1/22 +....) + (1/52 + 1/54 + 1/56 +......)
= r = (1/4)/(1/2) , r = (1/54)/(1/52)
⇒ r = 1/2 + 1/25
⇒ S = 1 + [(1/2)/(1-1/2)], S = [(1/25)/(1-1/25)]
⇒ S = 1 + 1, S = 1/24
Total sum = 2 + 1/24
⇒ 49/24
If the 10 times of the 10th term of an AP is equal to 15 times to the 15th term, then the 25th term is:- a)25 times of 25th term
- b)zero
- c)1
- d)2
Correct answer is option 'B'. Can you explain this answer?
If the 10 times of the 10th term of an AP is equal to 15 times to the 15th term, then the 25th term is:
a)
25 times of 25th term
b)
zero
c)
1
d)
2
|
|
Nandini Patel answered |
According to question ,
10 x 10th term =15 x 15th term
let a is the first term and d is the common difference .
10 (a+9d)=15 (a+14d)
5a+120d=0
a +24d=0
now ,
25th term =a+(25-1) d=a+24d=0
hence 25th term=0
How many terms of the G.P. 4 + 16 + 64 + … will make the sum 5460?- a)9
- b)7
- c)8
- d)6
Correct answer is option 'D'. Can you explain this answer?
How many terms of the G.P. 4 + 16 + 64 + … will make the sum 5460?
a)
9
b)
7
c)
8
d)
6
|
|
Nandini Iyer answered |
Sum (Sn) = a x (rn -1)/(r-1)
5460 = 4 x (4n -1)/3
16380 = 4n+1 - 4
5460 = 4 x (4n -1)/3
16380 = 4n+1 - 4
16384 = 4n+1
47 = 4n+1
7 = n + 1
n = 6
If a1, a2....an are in A.P. with common difference d ¹ 0, then the sum of the series(sin d) [cosec a1 cosec a2 + cosec a2 cosec a3 +..... ......+ cosec an – 1 cosec an]- a) sec a1 – sec an
- b)cosec a1 – cosec an
- c)cot a1 – cot an
- d) tan a1 – tan an
Correct answer is option 'C'. Can you explain this answer?
If a1, a2....an are in A.P. with common difference d ¹ 0, then the sum of the series
(sin d) [cosec a1 cosec a2 + cosec a2 cosec a3 +..... ......+ cosec an – 1 cosec an]
a)
sec a1 – sec an
b)
cosec a1 – cosec an
c)
cot a1 – cot an
d)
tan a1 – tan an
|
|
Krishna Iyer answered |
A₁ , A₂ , A₃ , .......An are in AP and common difference is d
so, d = A₂ - A₁ = A₃ - A₂ = A₄ - A₃ =...... =An - An-1 -------(1)
Now, sind[cosecA₁.cosecA₂ + cosecA₂.cosecA₃ + cosecA₃.cosecA₄ ...........+ cosecAn-1.cosecAn ]
⇒ sind[1/sinA₁.sinA₂ + 1/sinA₂.sinA₃ + 1/sinA₃.sinA₄ + .........+ 1/sinAn₋₁.sinAn]
⇒ sin d/sinA₁.sinA₂ + sind/sinA₂.sinA₃ + sind/sinA₃.sinA₄ + .......+sind/sinAn₋₁.sinAn
⇒ sin(A₂ - A₁)/sinA₁.sinA₂ + sin(A₃ - A₂)/sinA₂.sinA₃ + sin(A₄ - A₃)/sinA₃.sinA₄ + .......+ sin(An-1 - An)/sinAn-1.sinAn [ from equation (1)
⇒ (sinA₁.cosA₂ - cosA₁.sinA₂)/sinA₁.sinA₂ + (sinA₂.cosA₃ - cosA₂.sinA₃)/sinA₂.sinA₃ +.........+ (sinAn-1.cosAn - cosAn-1.sinAn)/sinAn-1.sinAn
⇒cotA₂ - cotA₁ + cotA₃ - cotA₂ + cotA₄ - cotA₃ + .........cotAn - cotAn-1
⇒cotAn - cotA₁
so, d = A₂ - A₁ = A₃ - A₂ = A₄ - A₃ =...... =An - An-1 -------(1)
Now, sind[cosecA₁.cosecA₂ + cosecA₂.cosecA₃ + cosecA₃.cosecA₄ ...........+ cosecAn-1.cosecAn ]
⇒ sind[1/sinA₁.sinA₂ + 1/sinA₂.sinA₃ + 1/sinA₃.sinA₄ + .........+ 1/sinAn₋₁.sinAn]
⇒ sin d/sinA₁.sinA₂ + sind/sinA₂.sinA₃ + sind/sinA₃.sinA₄ + .......+sind/sinAn₋₁.sinAn
⇒ sin(A₂ - A₁)/sinA₁.sinA₂ + sin(A₃ - A₂)/sinA₂.sinA₃ + sin(A₄ - A₃)/sinA₃.sinA₄ + .......+ sin(An-1 - An)/sinAn-1.sinAn [ from equation (1)
⇒ (sinA₁.cosA₂ - cosA₁.sinA₂)/sinA₁.sinA₂ + (sinA₂.cosA₃ - cosA₂.sinA₃)/sinA₂.sinA₃ +.........+ (sinAn-1.cosAn - cosAn-1.sinAn)/sinAn-1.sinAn
⇒cotA₂ - cotA₁ + cotA₃ - cotA₂ + cotA₄ - cotA₃ + .........cotAn - cotAn-1
⇒cotAn - cotA₁
Chapter doubts & questions for Sequences and Series - Chapter-wise Tests for JEE Main & Advanced 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Sequences and Series - Chapter-wise Tests for JEE Main & Advanced in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup
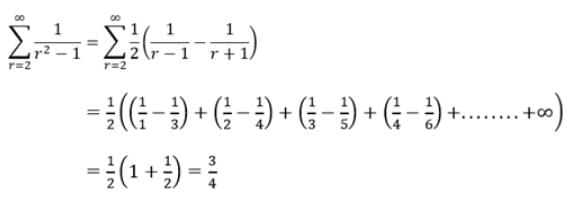


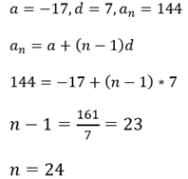
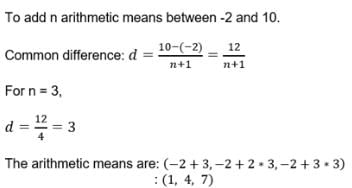
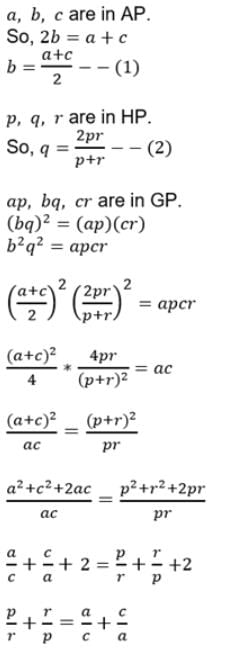

 Therefore
Therefore


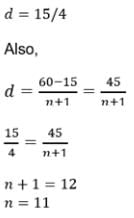
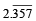 with recurring decimal is (1983 - 1 Mark)
with recurring decimal is (1983 - 1 Mark)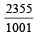
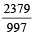
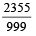
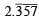 = 2 + .357 + 0.000357 + ...∞
= 2 + .357 + 0.000357 + ...∞