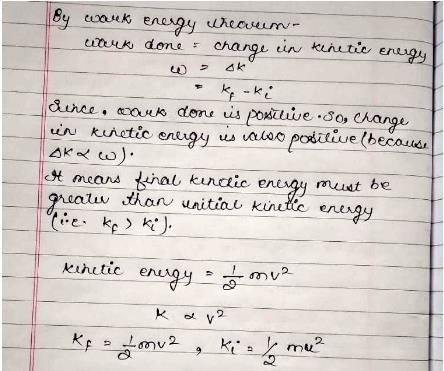All Exams >
NEET >
Physics Class 11 >
All Questions
All questions of Work, Energy and Power for NEET Exam
For what angle between Force and Displacement will the work done be positive?- a)

- b)
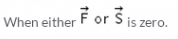
- c)

- d)

Correct answer is option 'C'. Can you explain this answer?
For what angle between Force and Displacement will the work done be positive?
a)
b)
c)
d)
|
|
Om Desai answered |
- If a force acting on a body has a component in the opposite direction of displacement, the work done is negative.
- So when a body slides against a rough horizontal surface, its displacement is opposite to that of the force of friction. The work done by the friction is negative.
Work done by gravitational force on a man, in lifting a bucket out of the well by rope tied to the bucket is- a)negative
- b)positive
- c)zero
- d)infinity
Correct answer is option 'A'. Can you explain this answer?
Work done by gravitational force on a man, in lifting a bucket out of the well by rope tied to the bucket is
a)
negative
b)
positive
c)
zero
d)
infinity
|
|
Om Desai answered |
When the man pulls the bucket outside the well the gravitational potential of the man + bucket system increases and hence the work done by the gravitational force is negative.
Two identical balls A and B moving with velocities +0.5 m/s and –0.3 m/s respectively, collide head on elastically. The velocities of the balls A and B after collision, will be, respectively [1991]- a)+0.5 m/s and +0.3 m/s
- b)– 0.3 m/s and +0.5 m/s
- c)+0.3 m/s and 0.5 m/s
- d)–0.5 m/s and +0.3 m/s
Correct answer is option 'B'. Can you explain this answer?
Two identical balls A and B moving with velocities +0.5 m/s and –0.3 m/s respectively, collide head on elastically. The velocities of the balls A and B after collision, will be, respectively [1991]
a)
+0.5 m/s and +0.3 m/s
b)
– 0.3 m/s and +0.5 m/s
c)
+0.3 m/s and 0.5 m/s
d)
–0.5 m/s and +0.3 m/s

|
Kajal Bose answered |
When the identical balls collide head-on, their velocities are exchanged.
Time rate at which work is done by a force is- a)Power
- b)Torque
- c)Centrifugal Force
- d)Acceleration
Correct answer is option 'A'. Can you explain this answer?
Time rate at which work is done by a force is
a)
Power
b)
Torque
c)
Centrifugal Force
d)
Acceleration
|
|
Gaurav Kumar answered |
We know that Work done, W = F.s
where F is force and s is displacement due to that force.
Thus rate of work done is:
where F is force and s is displacement due to that force.
Thus rate of work done is:
dW/dt = d(F.s)/dt
So as F is constant we get,
dW/dt = F.d(s)/dt = F.v = P (Power)
dW/dt = F.d(s)/dt = F.v = P (Power)
There are two bodies X and Y with equal kinetic energy but different masses m and 4m respectively. The ratio of their linear momentum is-- a)1:2
- b)4:1
- c)1:√2
- d)1:4
Correct answer is option 'A'. Can you explain this answer?
There are two bodies X and Y with equal kinetic energy but different masses m and 4m respectively. The ratio of their linear momentum is-
a)
1:2
b)
4:1
c)
1:√2
d)
1:4
|
|
Suresh Iyer answered |
X and Y have equal kinetic energy but their masses are m and 4m respectively.
► 1/2 m1v12 = 1/2 m2v22
► mv12 = 4m * v22
► v1 : v2 = 2 : 1
Hence the ratio of their linear momentum is:
m1v1 : m2v2 = m * 2v : 4m * v = 1 : 2
► 1/2 m1v12 = 1/2 m2v22
► mv12 = 4m * v22
► v1 : v2 = 2 : 1
Hence the ratio of their linear momentum is:
m1v1 : m2v2 = m * 2v : 4m * v = 1 : 2
By how much does kinetic energy increase if the momentum is increased by 20%?- a)55 %
- b)20 %
- c)44 %
- d)60 %
Correct answer is option 'C'. Can you explain this answer?
By how much does kinetic energy increase if the momentum is increased by 20%?
a)
55 %
b)
20 %
c)
44 %
d)
60 %
|
|
Hansa Sharma answered |
The kinetic energy is given by:
KE= p2/2m
So, ΔKE = 2pΔp / 2m = pΔp / m
ΔKE / KE = (pΔp/m) * (2m/p2) = 2Δp / p
Since the momentum p increases by 20%, so the final momentum becomes 1.2p.
Hence, KEfinal = (1.2p)2 / 2m = 1.44p2 / 2m = 1.44KE
So, % change in KE = 44%
ΔKE / KE = (pΔp/m) * (2m/p2) = 2Δp / p
Since the momentum p increases by 20%, so the final momentum becomes 1.2p.
Hence, KEfinal = (1.2p)2 / 2m = 1.44p2 / 2m = 1.44KE
So, % change in KE = 44%
Output of a truck is 4500 J and its efficiency is 50%, the input energy provided to the truck is- a)5000 J
- b)900 J
- c)9000 J
- d)500 J
Correct answer is option 'C'. Can you explain this answer?
Output of a truck is 4500 J and its efficiency is 50%, the input energy provided to the truck is
a)
5000 J
b)
900 J
c)
9000 J
d)
500 J
|
|
Naina Sharma answered |
► η = work output / heat input
► η = 50% = 50/100 = 1/2
► 1/2 = 4500 / Heat input
► Heat input = 9000 J
► η = 50% = 50/100 = 1/2
► 1/2 = 4500 / Heat input
► Heat input = 9000 J
Water falls from a height of 60 m at the rate of 15 kg/s to operate a turbine. The losses due to frictional force are 10% of energy. How much power is generated by the turbine?( g = 10 m/s2) [2008]
- a)8.1 kW
- b)10.2 kW
- c)12.3 kW
- d)7.0 kW
Correct answer is option 'A'. Can you explain this answer?
Water falls from a height of 60 m at the rate of 15 kg/s to operate a turbine. The losses due to frictional force are 10% of energy. How much power is generated by the turbine?( g = 10 m/s2) [2008]
a)
8.1 kW
b)
10.2 kW
c)
12.3 kW
d)
7.0 kW

|
Arnav Iyer answered |
Given, h = 60m, g = 10 ms–2, Rate of flow of water = 15 kg/s
∴ Power of the falling water = 15 kgs–1 × 10 ms–2 × 60 m = 900 watt.
Loss in energy due to friction
Loss in energy due to friction
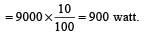
∴ Power generated by the turbine = ( 9000 – 900) watt = 8100 watt = 8.1 kW
A machine gun fires 60 bullets per minute, with a velocity of 700 m/s. If each bullet has a mass of 50g, find the power developed by the gun.
- a)1225 W
- b)12250 W
- c)122.5 W
- d)122 W
Correct answer is option 'B'. Can you explain this answer?
A machine gun fires 60 bullets per minute, with a velocity of 700 m/s. If each bullet has a mass of 50g, find the power developed by the gun.
a)
1225 W
b)
12250 W
c)
122.5 W
d)
122 W
|
|
Tejas Verma answered |
Each bullet will have KE = 1/2 * 0.05 * 700 * 700 = 12250 J
So for 60 bullets the energy given by machine in 60 second = 60 x 12250 J
Hence power developed = Energy / time =60 x12250/60 =12250W
Or power = 12.250 kW.
So for 60 bullets the energy given by machine in 60 second = 60 x 12250 J
Hence power developed = Energy / time =60 x12250/60 =12250W
Or power = 12.250 kW.
Which of the following is not conserved in inelastic collision?- a)momentum
- b)kinetic energy
- c)both momentum and kinetic energy
- d)neither momentum nor kinetic energ
Correct answer is option 'B'. Can you explain this answer?
Which of the following is not conserved in inelastic collision?
a)
momentum
b)
kinetic energy
c)
both momentum and kinetic energy
d)
neither momentum nor kinetic energ
|
|
Rajesh Gupta answered |
In an inelastic collision, the force of reformation is not equal to the force of deformation and thus some amount of energy is lost. But still as no external force acts upon the system momentum is still conserved.
A bomb of mass 30 kg at rest explodes into two pieces of masses 18 kg and 12 kg. The velocity of 18 kg mass is 6 ms–1. The kinetic energy of the other mass is [2005]- a)324 J
- b)486 J
- c)256 J
- d)524 J
Correct answer is option 'B'. Can you explain this answer?
A bomb of mass 30 kg at rest explodes into two pieces of masses 18 kg and 12 kg. The velocity of 18 kg mass is 6 ms–1. The kinetic energy of the other mass is [2005]
a)
324 J
b)
486 J
c)
256 J
d)
524 J

|
Sarthak Saini answered |
From conservation of linear momentum
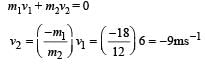
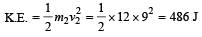
Which of the following statement is not related to conservative force?- a)Work done in closed path is zero
- b)Work done is recoverable
- c)Path independent
- d)Path dependent
Correct answer is option 'D'. Can you explain this answer?
Which of the following statement is not related to conservative force?
a)
Work done in closed path is zero
b)
Work done is recoverable
c)
Path independent
d)
Path dependent
|
|
Krishna Iyer answered |
A force is said to be conservative if the work done by or against the force on a body is independent of path followed by the body and depends only on initial and final positions.
Work done by or against the conservative force in moving a particle along a closed path is zero.
Work done by or against the conservative force in moving a particle along a closed path is zero.
Which of the following is not a unit of energy?- a)newton meter
- b)electron volt
- c)joule/meter
- d)kilowatt hour
Correct answer is option 'C'. Can you explain this answer?
Which of the following is not a unit of energy?
a)
newton meter
b)
electron volt
c)
joule/meter
d)
kilowatt hour

|
Gargey Dudhe answered |
C is correct option because energy The joule ( symbol: J) is a derived unit of energy in the International System of Units. It is equal to the energy transferred to (or work done on) an object when a force of one newton acts on that object in the direction of its motion through a distance of one metre (1 newton metreor N⋅m). pls upvote and follow me.
In an elastic collision in one dimension if a body A collides against the body B of equal mass at rest, then the body A will- a)moves with the same velocity but in opposite direction
- b)move with twice its initial velocity
- c)moves with the same velocity in the same direction
- d)come to rest.
Correct answer is option 'D'. Can you explain this answer?
In an elastic collision in one dimension if a body A collides against the body B of equal mass at rest, then the body A will
a)
moves with the same velocity but in opposite direction
b)
move with twice its initial velocity
c)
moves with the same velocity in the same direction
d)
come to rest.
|
|
Lavanya Menon answered |
Since collision is elastic and mass is same then after velocity exchange A body will stop and B will start moving with A's velocity in the same direction.
Two moving particle P and Q are 10 m apart at a certain instant. The velocity of P is 8m/s making an angle 30° with the line joining P and Q and that of Q is 6m/s making an angle 30° with PQ as shown in the figure. Then angular velocity of P with respect to Q is 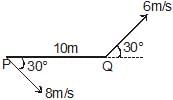
- a)Zero
- b)0.1 rad/sec
- c)0.4 rad/sec
- d)0.7 rad sec
Correct answer is option 'D'. Can you explain this answer?
Two moving particle P and Q are 10 m apart at a certain instant. The velocity of P is 8m/s making an angle 30° with the line joining P and Q and that of Q is 6m/s making an angle 30° with PQ as shown in the figure. Then angular velocity of P with respect to Q is
a)
Zero
b)
0.1 rad/sec
c)
0.4 rad/sec
d)
0.7 rad sec
|
|
Krishna Iyer answered |
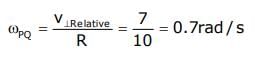
A machine, in an amusement park, consists of a cage at the end of one arm, hinged at O. The cage revolves along a vertical circle of radius r (ABCDEFGH) about its hinge O, at constant linear speedv = 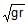 . The cage is so attached that the man of weight `w' standing on a weighing machine, inside the cage, is always vertical. Then which of the following is correct
. The cage is so attached that the man of weight `w' standing on a weighing machine, inside the cage, is always vertical. Then which of the following is correct
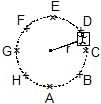
- a)The reading of his weight on the machine is the same at all positions
- b)The weight reading at A is greater than the weight reading at E by 2 w.
- c)The weight reading at G = w
- d)The ratio of the weight reading at E to that at A=0
- e)The ratio of the weight reading at A to that at C=2
Correct answer is option 'B,C,D,E'. Can you explain this answer?
A machine, in an amusement park, consists of a cage at the end of one arm, hinged at O. The cage revolves along a vertical circle of radius r (ABCDEFGH) about its hinge O, at constant linear speed
v = 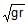 . The cage is so attached that the man of weight `w' standing on a weighing machine, inside the cage, is always vertical. Then which of the following is correct
. The cage is so attached that the man of weight `w' standing on a weighing machine, inside the cage, is always vertical. Then which of the following is correct

a)
The reading of his weight on the machine is the same at all positions
b)
The weight reading at A is greater than the weight reading at E by 2 w.
c)
The weight reading at G = w
d)
The ratio of the weight reading at E to that at A=0
e)
The ratio of the weight reading at A to that at C=2

|
Crafty Classes answered |

No work is done by a force on an object if- a)The force is always perpendicular to its velocity
- b)The force is always perpendicular to its acceleration
- c)The object is stationary but the point of application of the force moves on the object.
- d)The object moves in such a way that the point of application of the force remains fixed.
Correct answer is option 'A,B'. Can you explain this answer?
No work is done by a force on an object if
a)
The force is always perpendicular to its velocity
b)
The force is always perpendicular to its acceleration
c)
The object is stationary but the point of application of the force moves on the object.
d)
The object moves in such a way that the point of application of the force remains fixed.
|
|
Krishna Iyer answered |
Work done = f.ds
So on perpendicular application for product becomes zero so no work is done
So on perpendicular application for product becomes zero so no work is done
When a ball is allowed to fall from a height of 20 m, 40% of its energy is lost due to impact. After one impact the ball will go up to a height of- a)12 m
- b)15 m
- c)8 m
- d)10 m
Correct answer is option 'A'. Can you explain this answer?
When a ball is allowed to fall from a height of 20 m, 40% of its energy is lost due to impact. After one impact the ball will go up to a height of
a)
12 m
b)
15 m
c)
8 m
d)
10 m
|
|
Lavanya Menon answered |
Before the impact the KE was ½ x m x (2g x 20) = 20mg
And let say v be the velocity after impact and for height h, v2= 2gh
Thus KE = ½ mv2 = ½m2gh = ⅗ x 20mg
Thus we get mgh = 12mg
thus h = 12 m
And let say v be the velocity after impact and for height h, v2= 2gh
Thus KE = ½ mv2 = ½m2gh = ⅗ x 20mg
Thus we get mgh = 12mg
thus h = 12 m
Frictional force is an example of- a)ectrostatic force
- b)Non conservative force
- c)conservative force
- d)nuclear force
Correct answer is option 'B'. Can you explain this answer?
Frictional force is an example of
a)
ectrostatic force
b)
Non conservative force
c)
conservative force
d)
nuclear force
|
|
Om Desai answered |
The friction is the phenomena that defines that there is a resistance which is present there between the two surfaces. This friction is applied tangentially to the surfaces in contact. Thus the main thing is that the forces on both of the surfaces act tangential to each other.
When conservative force does positive work on a body, the potential energy of the body:- a)increases
- b)decreases
- c)remains unaltered
- d)there is no relationship between force and potential energy
Correct answer is option 'B'. Can you explain this answer?
When conservative force does positive work on a body, the potential energy of the body:
a)
increases
b)
decreases
c)
remains unaltered
d)
there is no relationship between force and potential energy
|
|
Suresh Iyer answered |
We have a relation between potential energy and work done: 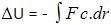
The negative sign just shows the inverse relation between potential energy and work done by conservative force.
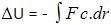
The negative sign just shows the inverse relation between potential energy and work done by conservative force.
The potential energy of a system increases if work is done [2011]- a)upon the system by a n on conser vative force
- b)upon the system by a conservative force
- c)by the system against a non conservative force
- d)by the system against a conservative force
Correct answer is option 'D'. Can you explain this answer?
The potential energy of a system increases if work is done [2011]
a)
upon the system by a n on conser vative force
b)
upon the system by a conservative force
c)
by the system against a non conservative force
d)
by the system against a conservative force
|
|
Avantika Kumar answered |
Explanation:
When work is done on a system against a conservative force, the potential energy of the system increases.
- Conservative Force: A force is said to be conservative if the work done by the force on a particle moving from one point to another depends only on the initial and final positions of the particle and not on the path followed by the particle.
- Potential Energy: Potential energy is the energy possessed by a system due to the relative positions of its components. It is a scalar quantity and is measured in joules (J).
In the given options, only option D mentions work done by the system against a conservative force, which is the correct answer.
When a system does work against a conservative force, the energy is stored in the system as potential energy. This potential energy can be released later when the system returns to its original position or configuration.
For example, when a spring is compressed by an external force, the system stores potential energy. When the external force is removed, the spring returns to its original position and releases the stored potential energy.
Hence, the potential energy of a system increases when work is done by the system against a conservative force.
When work is done on a system against a conservative force, the potential energy of the system increases.
- Conservative Force: A force is said to be conservative if the work done by the force on a particle moving from one point to another depends only on the initial and final positions of the particle and not on the path followed by the particle.
- Potential Energy: Potential energy is the energy possessed by a system due to the relative positions of its components. It is a scalar quantity and is measured in joules (J).
In the given options, only option D mentions work done by the system against a conservative force, which is the correct answer.
When a system does work against a conservative force, the energy is stored in the system as potential energy. This potential energy can be released later when the system returns to its original position or configuration.
For example, when a spring is compressed by an external force, the system stores potential energy. When the external force is removed, the spring returns to its original position and releases the stored potential energy.
Hence, the potential energy of a system increases when work is done by the system against a conservative force.
If the kinetic energy of a particle is increased by 300%, the momentum of the particle will increase by[2002]- a)20%
- b)200%
- c)100%
- d)50%
Correct answer is option 'C'. Can you explain this answer?
If the kinetic energy of a particle is increased by 300%, the momentum of the particle will increase by[2002]
a)
20%
b)
200%
c)
100%
d)
50%

|
Pooja Saha answered |
New K.E., E' = 4E
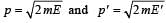
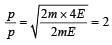
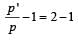
[on substrating 1 in both sides.]
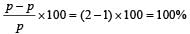
Two cylindrical vessels of equal cross-sectional area 16 cm2 contain water up to heights 100 cm and 150 cm, respectively. The vessels are interconnected so that the water levels in them become equal. The work done by the force of gravity during the process is: [Take density of water = 103 kg/m3 and g = 10 ms-2]
- a)0.25 J
- b)12 J
- c)8 J
- d)1 J
Correct answer is option 'D'. Can you explain this answer?
Two cylindrical vessels of equal cross-sectional area 16 cm2 contain water up to heights 100 cm and 150 cm, respectively. The vessels are interconnected so that the water levels in them become equal. The work done by the force of gravity during the process is: [Take density of water = 103 kg/m3 and g = 10 ms-2]
a)
0.25 J
b)
12 J
c)
8 J
d)
1 J
|
|
Rajeev Saxena answered |
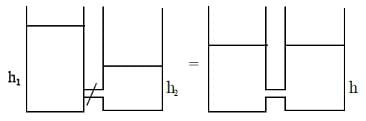
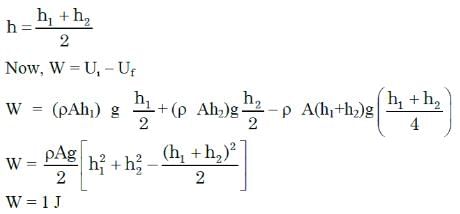
Which of the following statements is false:- a)kinetic energy is positiv
- b)potential energy is positive
- c)kinetic energy is negative
- d)potential energy is negative
Correct answer is option 'C'. Can you explain this answer?
Which of the following statements is false:
a)
kinetic energy is positiv
b)
potential energy is positive
c)
kinetic energy is negative
d)
potential energy is negative

|
Aiims answered |
K.E never negative as velocity negative then its square becomes it positive.
Select the odd one out- a)Viscous force
- b)Frictional force
- c)Electrostatic force
- d)Air-resistance
Correct answer is option 'C'. Can you explain this answer?
Select the odd one out
a)
Viscous force
b)
Frictional force
c)
Electrostatic force
d)
Air-resistance
|
|
Anjali Iyer answered |
The correct answer is muscular force because all these forces are non-contact forces and muscular force is a contact force.
A bomb of mass 4 kg explodes in air into two pieces of masses 3 kg and 1 kg. The smaller mass goes at a speed of 90 m/s. The total energy imparted to two fragments is.- a)2.4 kj
- b)5.4 kj
- c)5.9 kJ
- d)3.8 kJ
Correct answer is option 'B'. Can you explain this answer?
A bomb of mass 4 kg explodes in air into two pieces of masses 3 kg and 1 kg. The smaller mass goes at a speed of 90 m/s. The total energy imparted to two fragments is.
a)
2.4 kj
b)
5.4 kj
c)
5.9 kJ
d)
3.8 kJ
|
|
Raghav Bansal answered |
By conservation of momentum we get the speed of the bigger part let say, v = 1 x90 / 3
Hence we get v = 30
Thus the total KE of the system after collision is ½ (3 X 900 + 1 X 8100)
Thus KE = ½ (10800) = 5400
Now if we apply WET to the system, as no external force has acted upon it, we get
W = ΔKE
= 5400 - 0
= 5.4 kJ
Hence we get v = 30
Thus the total KE of the system after collision is ½ (3 X 900 + 1 X 8100)
Thus KE = ½ (10800) = 5400
Now if we apply WET to the system, as no external force has acted upon it, we get
W = ΔKE
= 5400 - 0
= 5.4 kJ
A bomb at rest on a horizontal frictionless surface explodes and breaks into three pieces that fly apart horizontally as shown below. Select all of the following statements that must be true after the bomb has exploded.1. The total kinetic energy of the bomb fragments is the same as that of the bomb before explosion.
2. The total momentum of the bomb fragments is the same as that of the bomb before explosion.
3. The total momentum of all the bomb fragments together is zero.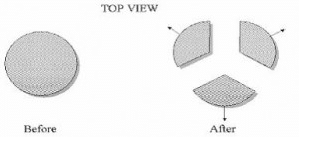
- a)1,2 and 3
- b)1 only
- c)3 only
- d)2 only
Correct answer is option 'C'. Can you explain this answer?
A bomb at rest on a horizontal frictionless surface explodes and breaks into three pieces that fly apart horizontally as shown below. Select all of the following statements that must be true after the bomb has exploded.
1. The total kinetic energy of the bomb fragments is the same as that of the bomb before explosion.
2. The total momentum of the bomb fragments is the same as that of the bomb before explosion.
3. The total momentum of all the bomb fragments together is zero.
2. The total momentum of the bomb fragments is the same as that of the bomb before explosion.
3. The total momentum of all the bomb fragments together is zero.
a)
1,2 and 3
b)
1 only
c)
3 only
d)
2 only
|
|
Naina Sharma answered |
So as no external force acts upon the system, we can say that momentum of the system remains conserved but as an internal force acts that explodes the bomb, the KE of the system is never conserved. But every fragment has some non zero momentum while the bomb initially has zero momentum.
For a conservative force, F is equal to- a)
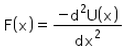
- b)
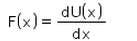
- c)
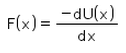
- d)
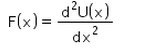
Correct answer is option 'C'. Can you explain this answer?
For a conservative force, F is equal to
a)
b)
c)
d)
|
|
Pooja Shah answered |
Potential energy at a point is defined in terms the amount of work done, which is defined in terms of force and thus we get potential as an integral of force applied over some position x. Hence F(x) = -dU(x) / dx which is the differentiation of potential energy wrt position.
If a force acts perpendicular to the direction of motion of a body, what is the amount of work done?- a)Infinity
- b)Constant
- c)Zero
- d)sinθ
Correct answer is option 'C'. Can you explain this answer?
If a force acts perpendicular to the direction of motion of a body, what is the amount of work done?
a)
Infinity
b)
Constant
c)
Zero
d)
sinθ
|
|
Anjali Sharma answered |
If a force acts perpendicular to the direction of a body, the amount of work done is zero because there is no displacement in the direction of a force.
A 0.5 kg ball moving with speed of 12 m/s strikes a hard wall at an angle of 30° with the wall. It is reflected with the same speed and at the same angle. If the ball is in contact with the wall for 0.25 seconds, the average force acting on the wall is[2006]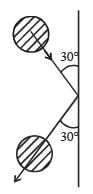
- a)24 N
- b)12 N
- c)96 N
- d)48 N
Correct answer is option 'A'. Can you explain this answer?
A 0.5 kg ball moving with speed of 12 m/s strikes a hard wall at an angle of 30° with the wall. It is reflected with the same speed and at the same angle. If the ball is in contact with the wall for 0.25 seconds, the average force acting on the wall is[2006]

a)
24 N
b)
12 N
c)
96 N
d)
48 N

|
Ias Masters answered |
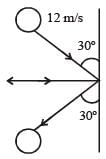
Resolving the velocities in vertical and horizontal directions, resolved parts of first velocity
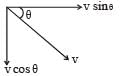
v cosθ perpendicular to the wall and v sinθ parallel to the wall. In the second case, they are –v sinθ & v cosθ respectively. Here, –ve sign is because direction is opposite to the earlier ones. So we see a net change in velocity perpendicular to way = v sinθ – (–v sinθ) = 2v sinθ
This change has occured in 0.25 sec, so, rate of change of velocity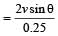
This change has occured in 0.25 sec, so, rate of change of velocity
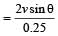
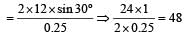
Thus, acceleration a = 48 m/sec2
Force applied = m . a = 0.5 × 48 = 24 N
A shell of mass 200 gm is ejected from a gun of mass 4 kg by an explosion that generates 1.05 kJ of energy. The initial velocity of the shell is:- a)100 ms–1
- b)80 ms–1 [2008]
- c)40 ms–1
- d)120 ms–1
Correct answer is option 'A'. Can you explain this answer?
A shell of mass 200 gm is ejected from a gun of mass 4 kg by an explosion that generates 1.05 kJ of energy. The initial velocity of the shell is:
a)
100 ms–1
b)
80 ms–1 [2008]
c)
40 ms–1
d)
120 ms–1
|
|
Rajeev Saxena answered |
Solution: Option A is correct option.
Explanation is given as follows.
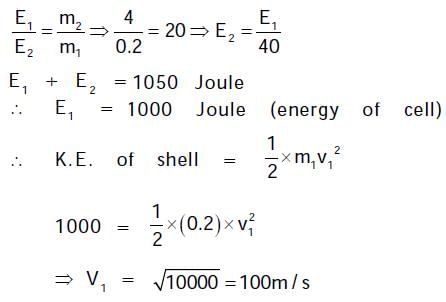
A box of mass m is released from rest at position on the frictionless curved track shown. It slides a distance d along the track in time t to reach position 2, dropping a vertical distance h. Let v and a be the instantaneous speed and instantaneous acceleration, respectively, of the box at position 2. Which of the following equations is valid for this situation? 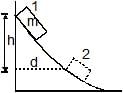
- a)h = vt
- b)h = (1/2)gt2
- c)mgh = (1/2)mv2
- d)none
Correct answer is option 'C'. Can you explain this answer?
A box of mass m is released from rest at position on the frictionless curved track shown. It slides a distance d along the track in time t to reach position 2, dropping a vertical distance h. Let v and a be the instantaneous speed and instantaneous acceleration, respectively, of the box at position 2. Which of the following equations is valid for this situation?
a)
h = vt
b)
h = (1/2)gt2
c)
mgh = (1/2)mv2
d)
none

|
Imk Pathsala answered |
According to the Work Energy Theorem,
Change in PE = Change in KE
So, mgh = ½ mv2
Hence C
Forum id- 1775160
For complete circle v = √(5gl)
mgh = ½mv2
So, h = 2.5R
Change in PE = Change in KE
So, mgh = ½ mv2
Hence C
Forum id- 1775160
For complete circle v = √(5gl)
mgh = ½mv2
So, h = 2.5R
A stone of mass of 16 kg is attached to a string 144 m long and is whirled in a horizontal smooth surface. The maximum tension the string can withstand is 16 newton. The maximum speed of revolution of the stone without breaking it, will be :- a)20 ms-1
- b)16 ms-1
- c)14 ms-1
- d)12 ms-1
Correct answer is option 'A,C,D'. Can you explain this answer?
A stone of mass of 16 kg is attached to a string 144 m long and is whirled in a horizontal smooth surface. The maximum tension the string can withstand is 16 newton. The maximum speed of revolution of the stone without breaking it, will be :
a)
20 ms-1
b)
16 ms-1
c)
14 ms-1
d)
12 ms-1
|
|
Pooja Shah answered |
T= (mv2max)/r
16 = (16 v2max)/144
v2max = 12 m/s
16 = (16 v2max)/144
v2max = 12 m/s
The launching mechanism of a toy gun consists of a spring of unknown spring constant. When the spring is compressed 0.120 m, the gun, when fired vertically, is able to launch a 35.0-g projectile to a maximum height of 20.0 m above the position of the projectile before firing. Neglecting all resistive forces, determine the spring constant.- a)903 N/m
- b)993 N/m
- c)953 N/m
- d)873 N/m
Correct answer is option 'C'. Can you explain this answer?
The launching mechanism of a toy gun consists of a spring of unknown spring constant. When the spring is compressed 0.120 m, the gun, when fired vertically, is able to launch a 35.0-g projectile to a maximum height of 20.0 m above the position of the projectile before firing. Neglecting all resistive forces, determine the spring constant.
a)
903 N/m
b)
993 N/m
c)
953 N/m
d)
873 N/m

|
Mrinalini Bose answered |
Explanation:
Potential energy of spring converted in to potential energy

The minimum value of H required so that the particle makes a complete vertical circle is given by- a)5 R
- b)4 R
- c)2.5 R
- d)2 R
Correct answer is option 'C'. Can you explain this answer?
The minimum value of H required so that the particle makes a complete vertical circle is given by
a)
5 R
b)
4 R
c)
2.5 R
d)
2 R
|
|
Hansa Sharma answered |
For complete circle v = √(5gl)
mgh = ½mv2
So, h = 2.5R
mgh = ½mv2
So, h = 2.5R
Which physical quantity is conserved during both elastic and inelastic collision?- a)Kinetic energy
- b)Potential energy
- c)Linear momentum
- d)Velocity
Correct answer is option 'C'. Can you explain this answer?
Which physical quantity is conserved during both elastic and inelastic collision?
a)
Kinetic energy
b)
Potential energy
c)
Linear momentum
d)
Velocity
|
|
Preeti Iyer answered |
Kinetic energy is conserved in elastic collisions, whereas kinetic energy is converted into other forms of energy during an inelastic collision. In both types of collisions, momentum is conserved.
If the momentum of a body is increased by 50%, then the percentage increase in its kinetic energy is[1995]- a)50%
- b)100%
- c)125%
- d)200%
Correct answer is option 'C'. Can you explain this answer?
If the momentum of a body is increased by 50%, then the percentage increase in its kinetic energy is[1995]
a)
50%
b)
100%
c)
125%
d)
200%
|
|
Anand Chaudhary answered |
Explanation:
Let the initial momentum (P) of the body be P and its initial kinetic energy (K) be K.
According to the question, the momentum of the body is increased by 50%.
Therefore, the new momentum (P') of the body is:
P' = P + (50/100) * P = 1.5P
The kinetic energy of a body is given by:
K = (1/2) * m * v^2
where m is the mass of the body and v is its velocity.
Since the mass of the body remains constant, the kinetic energy is directly proportional to the square of its velocity.
Let the initial velocity (v) of the body be v and its new velocity (v') be v'.
Since momentum is given by:
P = m * v
and
P' = m * v'
we can write:
m * v' = 1.5 * m * v
or
v' = (3/2) * v
Therefore, the new kinetic energy (K') of the body is:
K' = (1/2) * m * v'^2
Substituting the value of v' in the above equation, we get:
K' = (1/2) * m * (3/2)^2 * v^2
K' = (9/8) * K
Therefore, the percentage increase in kinetic energy is:
(K' - K)/K * 100%
= [(9/8)K - K]/K * 100%
= (1/8) * 100%
= 12.5%
Hence, the correct option is (c) 125%.
The magnitude of displacement of a particle moving in a circle of radius a with constant angular speed w varies with time t as- a)2 a sin wt
- b)
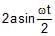
- c)2a cos wt
- d)

Correct answer is option 'B'. Can you explain this answer?
The magnitude of displacement of a particle moving in a circle of radius a with constant angular speed w varies with time t as
a)
2 a sin wt
b)
c)
2a cos wt
d)
|
|
Naina Sharma answered |
If a particle is moving with angular velocity=ω
Its angle of rotation is given by ωt
Now displacement= length of line AB
Position vector of a particle is given by
R =iacosωt + jasinωt
Ro=ai
displacement =R−Ro
=a(cosωt−1)i+asinωj
d=√[(a(cosωt-1))2+(asinω)2]
=a√(2(1-cosωt))=a√(2×2(sinωt/2)2)=2asinωt/2
Its angle of rotation is given by ωt
Now displacement= length of line AB
Position vector of a particle is given by
R =iacosωt + jasinωt
Ro=ai
displacement =R−Ro
=a(cosωt−1)i+asinωj
d=√[(a(cosωt-1))2+(asinω)2]
=a√(2(1-cosωt))=a√(2×2(sinωt/2)2)=2asinωt/2
A body projected ver tically fr om the ear th reaches a height equal to earth's radius before returning to the earth. The power exerted by the gravitational force is greatest [2011]- a)at the highest position of the body
- b)at the instant just before the body hits the earth
- c)it remains constant all through
- d)at the instant just after the body is projected
Correct answer is option 'B'. Can you explain this answer?
A body projected ver tically fr om the ear th reaches a height equal to earth's radius before returning to the earth. The power exerted by the gravitational force is greatest [2011]
a)
at the highest position of the body
b)
at the instant just before the body hits the earth
c)
it remains constant all through
d)
at the instant just after the body is projected
|
|
Anshika Roy answered |
**Answer:**
The power exerted by the gravitational force can be calculated using the formula:
Power = force x velocity
When a body is projected vertically upwards, the only force acting on it is the gravitational force. The gravitational force is given by:
F = mg
Where:
F = gravitational force
m = mass of the body
g = acceleration due to gravity
Since the body reaches a height equal to the Earth's radius, the distance traveled by the body is 2 times the Earth's radius. Let's assume the Earth's radius is R.
Therefore, the work done against the gravitational force is given by:
Work = force x distance
= mg x 2R
= 2mgR
Now, the time taken to reach the maximum height is given by:
t = (2u sinθ) / g
Where:
t = time taken
u = initial velocity
θ = angle of projection
g = acceleration due to gravity
Since the body is projected vertically upwards, the angle of projection is 90° and the sine of 90° is 1.
Therefore, the time taken to reach the maximum height is:
t = (2u) / g
Now, the power exerted by the gravitational force can be calculated using the formula:
Power = Work / time
= (2mgR) / [(2u) / g]
= mg^2R/u
From this equation, we can see that the power exerted by the gravitational force is inversely proportional to the initial velocity (u). As the body reaches the highest position, the velocity becomes zero. Therefore, the power exerted by the gravitational force is greatest at the highest position of the body.
Hence, the correct answer is option 'A' - at the highest position of the body.
The power exerted by the gravitational force can be calculated using the formula:
Power = force x velocity
When a body is projected vertically upwards, the only force acting on it is the gravitational force. The gravitational force is given by:
F = mg
Where:
F = gravitational force
m = mass of the body
g = acceleration due to gravity
Since the body reaches a height equal to the Earth's radius, the distance traveled by the body is 2 times the Earth's radius. Let's assume the Earth's radius is R.
Therefore, the work done against the gravitational force is given by:
Work = force x distance
= mg x 2R
= 2mgR
Now, the time taken to reach the maximum height is given by:
t = (2u sinθ) / g
Where:
t = time taken
u = initial velocity
θ = angle of projection
g = acceleration due to gravity
Since the body is projected vertically upwards, the angle of projection is 90° and the sine of 90° is 1.
Therefore, the time taken to reach the maximum height is:
t = (2u) / g
Now, the power exerted by the gravitational force can be calculated using the formula:
Power = Work / time
= (2mgR) / [(2u) / g]
= mg^2R/u
From this equation, we can see that the power exerted by the gravitational force is inversely proportional to the initial velocity (u). As the body reaches the highest position, the velocity becomes zero. Therefore, the power exerted by the gravitational force is greatest at the highest position of the body.
Hence, the correct answer is option 'A' - at the highest position of the body.
One coolie takes 1 minute to raise a suitcase through a height of 2 m but the second coolie takes 30 s to raise the same suitcase to the same height. The powers of two coolies are in the ratio of [NEET Kar. 2013]- a)1 : 2
- b)1 : 3
- c)2 : 1
- d)3 : 1
Correct answer is option 'A'. Can you explain this answer?
One coolie takes 1 minute to raise a suitcase through a height of 2 m but the second coolie takes 30 s to raise the same suitcase to the same height. The powers of two coolies are in the ratio of [NEET Kar. 2013]
a)
1 : 2
b)
1 : 3
c)
2 : 1
d)
3 : 1

|
Rajeev Sharma answered |
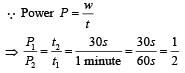
(t1 = 1 minute; t2 = 30 second given)
An explosion blows a rock into three parts. Two parts go off at right angles to each other. These two are, 1 kg first part moving with a velocity of 12 ms–1 and 2 kg second part moving with a velocity of 8 ms–1. If the third part flies off with a velocity of 4 ms–1, its mass would be: [2009]- a)7 kg
- b)17 kg
- c)3 kg
- d)5 kg
Correct answer is option 'D'. Can you explain this answer?
An explosion blows a rock into three parts. Two parts go off at right angles to each other. These two are, 1 kg first part moving with a velocity of 12 ms–1 and 2 kg second part moving with a velocity of 8 ms–1. If the third part flies off with a velocity of 4 ms–1, its mass would be: [2009]
a)
7 kg
b)
17 kg
c)
3 kg
d)
5 kg
|
|
Anoushka Kaur answered |
$^{-1}$ and 2 kg second part moving with a velocity of 8 ms$^{-1}$. What is the mass and velocity of the third part?
To solve this problem, we need to use the law of conservation of momentum. According to this law, the total momentum of a system of objects remains constant if there are no external forces acting on the system. In other words, the sum of the momenta of all the objects before the explosion is equal to the sum of the momenta of all the objects after the explosion.
Before the explosion, the rock had zero velocity, so its momentum was zero. After the explosion, the two parts that went off at right angles to each other have the following momenta:
First part: momentum = mass x velocity = 1 kg x 12 ms$^{-1}$ = 12 kg ms$^{-1}$
Second part: momentum = mass x velocity = 2 kg x 8 ms$^{-1}$ = 16 kg ms$^{-1}$
The total momentum of these two parts is:
Total momentum = 12 kg ms$^{-1}$ + 16 kg ms$^{-1}$ = 28 kg ms$^{-1}$
According to the law of conservation of momentum, the momentum of the third part must be equal and opposite to the total momentum of the first two parts. Let's call the mass of the third part "m" and its velocity "v". Then we have:
Momentum of third part = -28 kg ms$^{-1}$
Momentum = mass x velocity
Therefore:
-mv = -28 kg ms$^{-1}$
Solving for "m", we get:
m = 28/v
Now we can use the law of conservation of energy to find the velocity of the third part. According to this law, the total kinetic energy of a system of objects remains constant if there are no external forces acting on the system. In other words, the sum of the kinetic energies of all the objects before the explosion is equal to the sum of the kinetic energies of all the objects after the explosion.
Before the explosion, the rock had zero kinetic energy, so its total kinetic energy was zero. After the explosion, the two parts that went off at right angles to each other have the following kinetic energies:
First part: KE = 0.5 x mass x velocity$^2$ = 0.5 x 1 kg x (12 ms$^{-1}$)$^2$ = 72 J
Second part: KE = 0.5 x mass x velocity$^2$ = 0.5 x 2 kg x (8 ms$^{-1}$)$^2$ = 64 J
The total kinetic energy of these two parts is:
Total KE = 72 J + 64 J = 136 J
According to the law of conservation of energy, the kinetic energy of the third part must be equal to the difference between the total kinetic energy of the first two parts and the initial kinetic energy of the rock. The initial kinetic energy of the rock was zero, so we have:
KE of third part = Total KE - 0 = 136 J
Using the formula for kinetic energy, we can write:
0.5mv$^2$ = 136 J
Solving for "v", we get:
v = $\sqrt{\frac{272}{m}}$
Substituting
To solve this problem, we need to use the law of conservation of momentum. According to this law, the total momentum of a system of objects remains constant if there are no external forces acting on the system. In other words, the sum of the momenta of all the objects before the explosion is equal to the sum of the momenta of all the objects after the explosion.
Before the explosion, the rock had zero velocity, so its momentum was zero. After the explosion, the two parts that went off at right angles to each other have the following momenta:
First part: momentum = mass x velocity = 1 kg x 12 ms$^{-1}$ = 12 kg ms$^{-1}$
Second part: momentum = mass x velocity = 2 kg x 8 ms$^{-1}$ = 16 kg ms$^{-1}$
The total momentum of these two parts is:
Total momentum = 12 kg ms$^{-1}$ + 16 kg ms$^{-1}$ = 28 kg ms$^{-1}$
According to the law of conservation of momentum, the momentum of the third part must be equal and opposite to the total momentum of the first two parts. Let's call the mass of the third part "m" and its velocity "v". Then we have:
Momentum of third part = -28 kg ms$^{-1}$
Momentum = mass x velocity
Therefore:
-mv = -28 kg ms$^{-1}$
Solving for "m", we get:
m = 28/v
Now we can use the law of conservation of energy to find the velocity of the third part. According to this law, the total kinetic energy of a system of objects remains constant if there are no external forces acting on the system. In other words, the sum of the kinetic energies of all the objects before the explosion is equal to the sum of the kinetic energies of all the objects after the explosion.
Before the explosion, the rock had zero kinetic energy, so its total kinetic energy was zero. After the explosion, the two parts that went off at right angles to each other have the following kinetic energies:
First part: KE = 0.5 x mass x velocity$^2$ = 0.5 x 1 kg x (12 ms$^{-1}$)$^2$ = 72 J
Second part: KE = 0.5 x mass x velocity$^2$ = 0.5 x 2 kg x (8 ms$^{-1}$)$^2$ = 64 J
The total kinetic energy of these two parts is:
Total KE = 72 J + 64 J = 136 J
According to the law of conservation of energy, the kinetic energy of the third part must be equal to the difference between the total kinetic energy of the first two parts and the initial kinetic energy of the rock. The initial kinetic energy of the rock was zero, so we have:
KE of third part = Total KE - 0 = 136 J
Using the formula for kinetic energy, we can write:
0.5mv$^2$ = 136 J
Solving for "v", we get:
v = $\sqrt{\frac{272}{m}}$
Substituting
Two spheres A and B of masses m1 and m2 respectively collide. A is at rest initially and B is moving with velocity v along x-axis. After collision B has a velocity v/2 in a direction perpendicular to the original direction. The mass A moves after collision in the direction.
- a)Same as that of B [2012]
- b)Opposite to that of B
- c)θ = tan–1 (1/2) to the x-axis
- d)θ = tan–1 (–1/2) to the x-axis
Correct answer is option 'C'. Can you explain this answer?
Two spheres A and B of masses m1 and m2 respectively collide. A is at rest initially and B is moving with velocity v along x-axis. After collision B has a velocity v/2 in a direction perpendicular to the original direction. The mass A moves after collision in the direction.
a)
Same as that of B [2012]
b)
Opposite to that of B
c)
θ = tan–1 (1/2) to the x-axis
d)
θ = tan–1 (–1/2) to the x-axis
|
|
Kavya Choudhury answered |
Perpendicular to the original direction of B
d)Cannot be determined
Answer:
c) Perpendicular to the original direction of B
Explanation:
We can solve this problem using conservation of momentum and conservation of kinetic energy.
Before the collision, the total momentum of the system is:
p = m2v
Since sphere A is at rest, its momentum is zero.
The total kinetic energy of the system before the collision is:
K = (1/2)m2v^2
After the collision, the spheres move in different directions. Let the velocity of sphere A be u and the velocity of sphere B be w. Then, the total momentum of the system after the collision is:
p' = m1u + m2w
Since sphere B moves perpendicular to its original direction, we can write:
w = 2v
Using conservation of momentum, we have:
m2v = m1u + m2(2v)
Simplifying, we get:
u = (m2 - 2m1)v / m1
Now, using conservation of kinetic energy, we have:
(1/2)m1u^2 + (1/2)m2w^2 = (1/2)m2v^2
Substituting the values of u and w, we get:
(m2 - 2m1)v^2 = m1u^2
Simplifying, we get:
u = sqrt((m2 - 2m1)/m1) v
Since m1 and m2 are positive, (m2 - 2m1)/m1 is negative. Therefore, u is imaginary, which means that sphere A moves in a direction perpendicular to the original direction of sphere B. Hence, the answer is option c) Perpendicular to the original direction of B.
d)Cannot be determined
Answer:
c) Perpendicular to the original direction of B
Explanation:
We can solve this problem using conservation of momentum and conservation of kinetic energy.
Before the collision, the total momentum of the system is:
p = m2v
Since sphere A is at rest, its momentum is zero.
The total kinetic energy of the system before the collision is:
K = (1/2)m2v^2
After the collision, the spheres move in different directions. Let the velocity of sphere A be u and the velocity of sphere B be w. Then, the total momentum of the system after the collision is:
p' = m1u + m2w
Since sphere B moves perpendicular to its original direction, we can write:
w = 2v
Using conservation of momentum, we have:
m2v = m1u + m2(2v)
Simplifying, we get:
u = (m2 - 2m1)v / m1
Now, using conservation of kinetic energy, we have:
(1/2)m1u^2 + (1/2)m2w^2 = (1/2)m2v^2
Substituting the values of u and w, we get:
(m2 - 2m1)v^2 = m1u^2
Simplifying, we get:
u = sqrt((m2 - 2m1)/m1) v
Since m1 and m2 are positive, (m2 - 2m1)/m1 is negative. Therefore, u is imaginary, which means that sphere A moves in a direction perpendicular to the original direction of sphere B. Hence, the answer is option c) Perpendicular to the original direction of B.
The potential energy in joules of a particle of mass 1 kg moving in a plane is given by U = 3x + 4y, the position coordinates of the point being x and y, measured in meters. If the particle is initially at rest at (6, 4), then- a)Its acceleration is of magnitude 5 m/s2
- b)Its speed when it crosses the y-axis is 10 m/s
- c)It crosses the y-axis (x = 0) at y = _4
- d)It moves in a straight line passing through the origin (0, 0)
Correct answer is option 'A,B,C'. Can you explain this answer?
The potential energy in joules of a particle of mass 1 kg moving in a plane is given by U = 3x + 4y, the position coordinates of the point being x and y, measured in meters. If the particle is initially at rest at (6, 4), then
a)
Its acceleration is of magnitude 5 m/s2
b)
Its speed when it crosses the y-axis is 10 m/s
c)
It crosses the y-axis (x = 0) at y = _4
d)
It moves in a straight line passing through the origin (0, 0)
|
|
Pooja Shah answered |
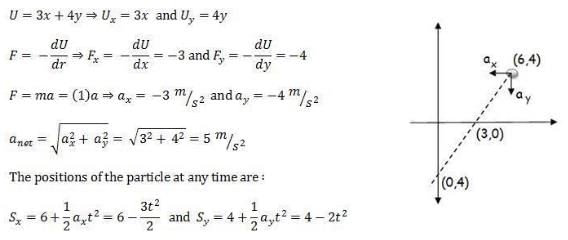
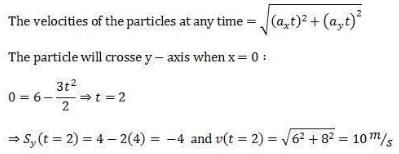 Similarly you can find that the particle crosses x - axis at (3, 0) with a velocity 7.07 m/s
Similarly you can find that the particle crosses x - axis at (3, 0) with a velocity 7.07 m/sWork done by force of friction- a)Can be zero
- b)Can be positive
- c)Can be negative
- d)Information insufficient
Correct answer is option 'A,B,C'. Can you explain this answer?
Work done by force of friction
a)
Can be zero
b)
Can be positive
c)
Can be negative
d)
Information insufficient
|
|
Om Desai answered |
Since the motion of the body can be placed in the direction of friction, opposite to the direction of motion and even can not be placed in any motion.
So, Work done by force of friction can be zero, negative, and can be positive.
So, Work done by force of friction can be zero, negative, and can be positive.
A force which does not depend on the path taken to increase the potential energy is- a)Viscous force
- b)Frictional force
- c)Conservative force
- d)Non - Conservative force
Correct answer is option 'C'. Can you explain this answer?
A force which does not depend on the path taken to increase the potential energy is
a)
Viscous force
b)
Frictional force
c)
Conservative force
d)
Non - Conservative force
|
|
Rohan Singh answered |
Gravitational and electrical forces are conservative. Friction is non-conservative because the amount of work done by friction depends on the path. One can associate a potential energy with a conservative force but not with a non-conservative force.
An engine pumps water through a hose pipe.Water passes through the pipe and leaves it with a velocity of 2 m/s. The mass per unit length of water in the pipe is 100 kg/m. What is the power of the engine? [2010]
- a)400 W
- b)200 W
- c)100 W
- d)800 W
Correct answer is option 'D'. Can you explain this answer?
An engine pumps water through a hose pipe.Water passes through the pipe and leaves it with a velocity of 2 m/s. The mass per unit length of water in the pipe is 100 kg/m. What is the power of the engine? [2010]
a)
400 W
b)
200 W
c)
100 W
d)
800 W
|
|
Nitya Shah answered |
Given:
Velocity of water, v = 2 m/s
Mass per unit length of water, m = 100 kg/m
To find:
Power of the engine
Formula used:
Power = Force × Velocity
Force = mass × acceleration = mass × change in velocity / time
Change in velocity = final velocity - initial velocity = v - 0 = v
Time taken to move out of the pipe, t = length of the pipe / velocity of water
Let the length of the pipe be L.
Therefore, t = L / v
Force = m × v / t = m × v² / L
Power = Force × Velocity = m × v² / L × v = m × v² / L
Substituting the given values, we get:
Power = 100 kg/m × (2 m/s)² / L = 400 W
Therefore, the power of the engine is 400 W.
Velocity of water, v = 2 m/s
Mass per unit length of water, m = 100 kg/m
To find:
Power of the engine
Formula used:
Power = Force × Velocity
Force = mass × acceleration = mass × change in velocity / time
Change in velocity = final velocity - initial velocity = v - 0 = v
Time taken to move out of the pipe, t = length of the pipe / velocity of water
Let the length of the pipe be L.
Therefore, t = L / v
Force = m × v / t = m × v² / L
Power = Force × Velocity = m × v² / L × v = m × v² / L
Substituting the given values, we get:
Power = 100 kg/m × (2 m/s)² / L = 400 W
Therefore, the power of the engine is 400 W.
There is a sphere of mass m moving with constant velocity v. It hits another sphere of same mass which is at rest. If e is the coefficient of restitution, then the ratio of the velocities of the two spheres after collision will be- a)
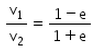
- b)
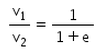
- c)
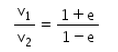
- d)
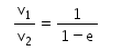
Correct answer is option 'A'. Can you explain this answer?
There is a sphere of mass m moving with constant velocity v. It hits another sphere of same mass which is at rest. If e is the coefficient of restitution, then the ratio of the velocities of the two spheres after collision will be
a)
b)
c)
d)
|
|
Gaurav Kumar answered |
Here, a sphere of mass m moving with a constant velocity v hits another stationary sphere of the same mass. As per the given problem we can write
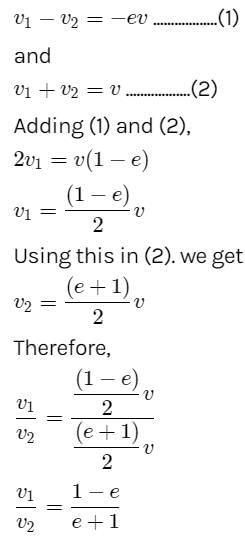
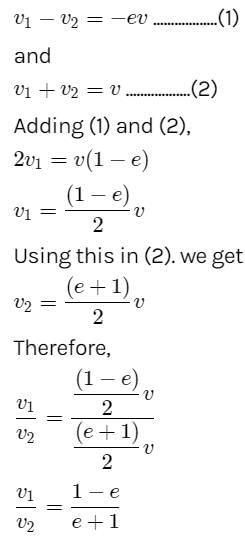
How much water, a pump of 2 kW can raise in one minute to a height of 10 m, take g = 10 m/s2? [1990]- a)1000 litres
- b)1200 litres
- c)100 litres
- d)2000 litres
Correct answer is option 'B'. Can you explain this answer?
How much water, a pump of 2 kW can raise in one minute to a height of 10 m, take g = 10 m/s2? [1990]
a)
1000 litres
b)
1200 litres
c)
100 litres
d)
2000 litres

|
Pooja Saha answered |
 Here, P = 2kW = 2000 W..
Here, P = 2kW = 2000 W..W = Mgh = M × 10 × 10 = 100 M and t = 60 s.
This gives, M = 1200 kg Its volume = 1200 litre as 1 litre of water contains 1 kg of its mass.
Chapter doubts & questions for Work, Energy and Power - Physics Class 11 2025 is part of NEET exam preparation. The chapters have been prepared according to the NEET exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for NEET 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Work, Energy and Power - Physics Class 11 in English & Hindi are available as part of NEET exam.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup