All questions of Pipes & Cistern for Computer Science Engineering (CSE) Exam
A pipe can fill a tank in 20 minutes but due to a leak develop at the bottom of the tank, 1/5 of the water filled by the pipe leaks out. Find the time in which the tank is filled.- a)20 min
- b)25 min
- c)30 min
- d)can’t be determined
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
A pipe can fill a tank in 20 minutes but due to a leak develop at the bottom of the tank, 1/5 of the water filled by the pipe leaks out. Find the time in which the tank is filled.
a)
20 min
b)
25 min
c)
30 min
d)
can’t be determined
e)
None of these
|
|
Nikita Singh answered |
Amount of tank filled by the pipe in one minute = 1/20 and due to leakage 1/5 of 1/20 leaks out so, [1/20 – (1/5)*(1/20)]*T = 1
We get T = 25
We get T = 25
On pipe P is 4 times faster than pipe Q and takes 45 minutes less than pipe Q. In what time the cistern is full if both the pipes are opened together?- a)8 minutes
- b)10 minutes
- c)12 minutes
- d)14 minutes
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
On pipe P is 4 times faster than pipe Q and takes 45 minutes less than pipe Q. In what time the cistern is full if both the pipes are opened together?
a)
8 minutes
b)
10 minutes
c)
12 minutes
d)
14 minutes
e)
None of these

|
Cstoppers Instructors answered |
Let P takes x minutes to fill the tank alone, then Q will take 4x minutes to fill the tank
4x – x = 45, x = 15
So P will take 15 minutes and Q will take 60 minutes to fill the tank. Both will fill the tank in
(60*15)/(75) = 12 minutes
4x – x = 45, x = 15
So P will take 15 minutes and Q will take 60 minutes to fill the tank. Both will fill the tank in
(60*15)/(75) = 12 minutes
Two pipes A and B can fill a tank in 12 hours and 15 hours respectively. If they are opened on alternate hours with pipe A opened first, then in how many hours the tank will be full?- a)13 hrs
- b)14 1/2 hrs
- c)12 hrs
- d)12 1/2 hrs
- e)10 2/3 hrs
Correct answer is option 'D'. Can you explain this answer?
Two pipes A and B can fill a tank in 12 hours and 15 hours respectively. If they are opened on alternate hours with pipe A opened first, then in how many hours the tank will be full?
a)
13 hrs
b)
14 1/2 hrs
c)
12 hrs
d)
12 1/2 hrs
e)
10 2/3 hrs

|
Bank Exams India answered |
A = 12 hours, B = 15 hours
Total work = LCM(12,15) = 60
So efficiency of A = 60/12 = 5, efficiency of B = 60/15 = 4
2 hrs work of (A+B) = 5+4 = 9
2*6(12) hours work of (A+B) = 9*6 = 54
So remaining work = 60-54 = 6
Now A’s turn at 13th hour, he will do remaining work(6) in 6/12 hr
So total 12 1/2 hrs
Total work = LCM(12,15) = 60
So efficiency of A = 60/12 = 5, efficiency of B = 60/15 = 4
2 hrs work of (A+B) = 5+4 = 9
2*6(12) hours work of (A+B) = 9*6 = 54
So remaining work = 60-54 = 6
Now A’s turn at 13th hour, he will do remaining work(6) in 6/12 hr
So total 12 1/2 hrs
In what time would a cistern be filled by three pipes whose diameters are 1cm, 2 cm and 3 cm running together, when the largest pipe alone can fill the tank in 21 minutes? The amount of water flowing through the pipe is directly proportional to the square of its diameter.- a)10.5 minutes
- b)11.5 minutes
- c)12.5 minutes
- d)13.5 minutes
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
In what time would a cistern be filled by three pipes whose diameters are 1cm, 2 cm and 3 cm running together, when the largest pipe alone can fill the tank in 21 minutes? The amount of water flowing through the pipe is directly proportional to the square of its diameter.
a)
10.5 minutes
b)
11.5 minutes
c)
12.5 minutes
d)
13.5 minutes
e)
None of these
|
|
User4237784 answered |
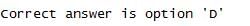
A cistern can be filled by a pipe in 6 hours. A leak is developed at the bottom due to which it takes 2 hours more to fill the cistern. Find the time taken by the leak to empty the cistern when the cistern is full.- a)20hr
- b)22hr
- c)24hr
- d)26hr
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
A cistern can be filled by a pipe in 6 hours. A leak is developed at the bottom due to which it takes 2 hours more to fill the cistern. Find the time taken by the leak to empty the cistern when the cistern is full.
a)
20hr
b)
22hr
c)
24hr
d)
26hr
e)
None of these
|
|
Kavya Saxena answered |
1/6 – 1/T = 1/8, solve for T
Pipe A fills a tank in 30 minutes. Pipe B can fill the same tank 5 times as fast as pipe A. If both the pipes were kept open when the tank is empty, how much time will it take for the tank to overflow?- a)3 minutes
- b)2 minutes
- c)5 minutes
- d)4 minutes
- e)None of the Above
Correct answer is option 'E'. Can you explain this answer?
Pipe A fills a tank in 30 minutes. Pipe B can fill the same tank 5 times as fast as pipe A. If both the pipes were kept open when the tank is empty, how much time will it take for the tank to overflow?
a)
3 minutes
b)
2 minutes
c)
5 minutes
d)
4 minutes
e)
None of the Above

|
Divya Garg answered |
Lets assume Total capacity 1000 Litres. 1 Pipe will fill 33.333 litres in 1 minute while 2nd pipe will fill 5 times faster i.e. 166.6666 litres . so total tank filled in 1minute is equal to 200 litres. so to fill 1000 litre tank it will take 1000/200= 5 Minutes. so to overflow the tank it requires more than 5 minutes.
One pipe fill 1/4 of the tank in 4 minutes and another pipe fills 1/5 of the tank in 4 minutes. Find the time taken by both pipe together to fill half the tank?- a)40/9 minutes
- b)50/9 minutes
- c)44/9 minutes
- d)53/9 minutes
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
One pipe fill 1/4 of the tank in 4 minutes and another pipe fills 1/5 of the tank in 4 minutes. Find the time taken by both pipe together to fill half the tank?
a)
40/9 minutes
b)
50/9 minutes
c)
44/9 minutes
d)
53/9 minutes
e)
None of these

|
Chirag Makkar answered |
First pipe will take 16 minutes to fill the tank alone. Similarly second pipe will take 20 minutes to fill the tank alone. Let T is the time in which both the pipes will fill half the tank
(1/16 + 1/20)*T = 1/2, we get T = 40/9 minutes
(1/16 + 1/20)*T = 1/2, we get T = 40/9 minutes
In what time a cistern is filled by three pipes of diameter 2cm, 4cm and 6cm respectively. If the time taken by largest pipe to fill the tank is 40 minutes. Amount of water flowing through the pipe is proportional to the diameter of the pipe- a)25.5/7 min
- b)25.3/7 min
- c)23.5/7 min
- d)23.4/7 min
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
In what time a cistern is filled by three pipes of diameter 2cm, 4cm and 6cm respectively. If the time taken by largest pipe to fill the tank is 40 minutes. Amount of water flowing through the pipe is proportional to the diameter of the pipe
a)
25.5/7 min
b)
25.3/7 min
c)
23.5/7 min
d)
23.4/7 min
e)
None of these

|
Divey Sethi answered |
Larger the cross-section area less will be time taken by pipe to fill the tank. 36/16 = T/40, T = 90min (for 4 cm pipe)
similarly for 2 cm pipe time taken will be = 360min
Total time = (1/360 + 1/90 + 1/40) = 1/p, so we get P = 25.5/7 minutes
similarly for 2 cm pipe time taken will be = 360min
Total time = (1/360 + 1/90 + 1/40) = 1/p, so we get P = 25.5/7 minutes
Three pipes, A, B and C are opened to fill a tank such that A and B cam fill the tank alone in 36 min. and 45 min. respectively and C can empty it in 30 min. After 6 minutes the emptying pipe is closed. In how many minutes the tank will be full in this way?- a)20
- b)25
- c)18
- d)24
- e)30
Correct answer is option 'D'. Can you explain this answer?
Three pipes, A, B and C are opened to fill a tank such that A and B cam fill the tank alone in 36 min. and 45 min. respectively and C can empty it in 30 min. After 6 minutes the emptying pipe is closed. In how many minutes the tank will be full in this way?
a)
20
b)
25
c)
18
d)
24
e)
30
|
|
Preeti Khanna answered |
Let the tank full in x minutes, then A and B opened for x minutes and C for 6 minutes.
(1/36 + 1/45)*x – (1/30)*6 = 1
(1/20)*x = 6/5
Solve, x = 24
(1/36 + 1/45)*x – (1/30)*6 = 1
(1/20)*x = 6/5
Solve, x = 24
A tank is normally filled in 6 hours but takes two hours longer to fill because of a leak in the bottom of the tank. If the tank is full the leak will empty it in how many hours?- a)16 hours
- b)18 hours
- c)17 hours
- d)24 hours
- e)None of the Above
Correct answer is option 'D'. Can you explain this answer?
A tank is normally filled in 6 hours but takes two hours longer to fill because of a leak in the bottom of the tank. If the tank is full the leak will empty it in how many hours?
a)
16 hours
b)
18 hours
c)
17 hours
d)
24 hours
e)
None of the Above

|
Bank Exams India answered |
Work done by leak in 1 hr=(1/6-1/8)=1/24
Leak will empty the tank in 24 hours
Leak will empty the tank in 24 hours
A pipe can fill a tank in 12 minutes and another pipe can fill it in 15 minutes, but a third pipe can empty it in 6 minutes. The first two pipes are kept open for 5 min in the beginning and then third pipe is also opened. Time taken to empty the water tank is?- a)30 mins
- b)25 mins
- c)45 mins
- d)50 mins
- e)None of the Above
Correct answer is option 'C'. Can you explain this answer?
A pipe can fill a tank in 12 minutes and another pipe can fill it in 15 minutes, but a third pipe can empty it in 6 minutes. The first two pipes are kept open for 5 min in the beginning and then third pipe is also opened. Time taken to empty the water tank is?
a)
30 mins
b)
25 mins
c)
45 mins
d)
50 mins
e)
None of the Above
|
|
Kavya Saxena answered |
x/6 – (x+5)/12 – (x+5)/15 = 0
x = 45 mins
x = 45 mins
Two pipes P and Q can fill a cistern in 10 hours and 20 hours respectively. If they are opened simultaneously. Sometimes later, tap Q was closed, then it takes total 8 hours to fill up the whole tank. After how many hours Q was closed?- a)4 hours
- b)5 hours
- c)2 hours
- d)6 hours
- e)None of the Above
Correct answer is option 'A'. Can you explain this answer?
Two pipes P and Q can fill a cistern in 10 hours and 20 hours respectively. If they are opened simultaneously. Sometimes later, tap Q was closed, then it takes total 8 hours to fill up the whole tank. After how many hours Q was closed?
a)
4 hours
b)
5 hours
c)
2 hours
d)
6 hours
e)
None of the Above

|
Vikas Singh answered |
Assume that the total volume of the cistern is 200L.
so, P fills 20L/hr and Q fills 10L/hr, and they both simultaneously fill 30L/hr
now, let Q was closed after x hrs and then rest was filled by P.
30x + 20(8-x)= 200
10x = 40 => x = 4 hrs
hence Q was closed after 4 hrs
so, P fills 20L/hr and Q fills 10L/hr, and they both simultaneously fill 30L/hr
now, let Q was closed after x hrs and then rest was filled by P.
30x + 20(8-x)= 200
10x = 40 => x = 4 hrs
hence Q was closed after 4 hrs
A bathing tub can be filled by a cold pipe in 15 minutes and by a hot pipe in 10 minutes. Ramesh opened both the tap and leaves the bathroom and returns at the time when the tub should be full. He observed that a waste pipe is opened at the bottom, he now closes it. Now the tub will take more 5 minutes to fill the tank, find the time in which the leak can empty the tank.- a)36/5 min
- b)33/5 min
- c)37/5 min
- d)can’t be determined
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
A bathing tub can be filled by a cold pipe in 15 minutes and by a hot pipe in 10 minutes. Ramesh opened both the tap and leaves the bathroom and returns at the time when the tub should be full. He observed that a waste pipe is opened at the bottom, he now closes it. Now the tub will take more 5 minutes to fill the tank, find the time in which the leak can empty the tank.
a)
36/5 min
b)
33/5 min
c)
37/5 min
d)
can’t be determined
e)
None of these

|
Divey Sethi answered |
(1/15 + 1/10 – 1/x)*6 + (1/15 + 1/10)*5 = 1
x = 36/5
x = 36/5
A Tank is already filled up to X% of its capacity. An Inlet pipe can fill Full Tank in 30 minutes and an Outlet pipe can empty Full Tank in 20 Minutes. Now both pipes are opened then the Tank is emptied in 24 Minutes. Then initially up to what % of its capacity is Tank filled?- a)40%
- b)48%
- c)50%
- d)60%
- e)Cannot be determined
Correct answer is option 'A'. Can you explain this answer?
A Tank is already filled up to X% of its capacity. An Inlet pipe can fill Full Tank in 30 minutes and an Outlet pipe can empty Full Tank in 20 Minutes. Now both pipes are opened then the Tank is emptied in 24 Minutes. Then initially up to what % of its capacity is Tank filled?
a)
40%
b)
48%
c)
50%
d)
60%
e)
Cannot be determined
|
|
Aisha Gupta answered |
1/30 – 1/20 = -1/60
Full Tank can be emptied 60 Minutes
In 24 minutes 40% of Tank can be emptied.
Full Tank can be emptied 60 Minutes
In 24 minutes 40% of Tank can be emptied.
Two pipes M and N can fill a tank in 30 and 45 minutes respectively. If both the pipes were open for few minutes after N was closed and the tank was full in 25 minutes, find the time for pipe N was open.- a)8.16m
- b)7.5min
- c)5min
- d)10.2m
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
Two pipes M and N can fill a tank in 30 and 45 minutes respectively. If both the pipes were open for few minutes after N was closed and the tank was full in 25 minutes, find the time for pipe N was open.
a)
8.16m
b)
7.5min
c)
5min
d)
10.2m
e)
None of these
|
|
Preeti Khanna answered |
X(1/30+1/45) + 1/30(25-x) = 1
x/45+25/30 =1
x/45 = 5/30 =1/6
x=45/6
x=7.5m
x/45+25/30 =1
x/45 = 5/30 =1/6
x=45/6
x=7.5m
A cistern is filled by 3 pipes A, B and C with uniform flow. The second pipe B takes3/2 times the time taken by A to fill the tank, while C takes twice the time taken by B to fill the tank. If all the three pipes can fill the tank in 7 hours, find the time required by pipe A alone to fill the tank.- a)10hrs
- b)12hrs
- c)14hrs
- d)15hrs
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
A cistern is filled by 3 pipes A, B and C with uniform flow. The second pipe B takes3/2 times the time taken by A to fill the tank, while C takes twice the time taken by B to fill the tank. If all the three pipes can fill the tank in 7 hours, find the time required by pipe A alone to fill the tank.
a)
10hrs
b)
12hrs
c)
14hrs
d)
15hrs
e)
None of these
|
|
Preeti Khanna answered |
1/x + 1/ (3/2x) + ½(3x/2) = 1/7
6/3x = 1/7
3x/6 = 7
3x=42
X=14
6/3x = 1/7
3x/6 = 7
3x=42
X=14
Two Inlet Pipes A and B together can fill a Tank in ‘X’ minutes. If A and B take 81 minutes and 49 minutes more than ‘X’ minutes respectively, to fill the Tank. Then They can fill the 5/7 of that Tank in how many minutes?- a)45 Minutes
- b)49 Minutes
- c)63 Minutes
- d)81 Minutes
- e)None
Correct answer is option 'A'. Can you explain this answer?
Two Inlet Pipes A and B together can fill a Tank in ‘X’ minutes. If A and B take 81 minutes and 49 minutes more than ‘X’ minutes respectively, to fill the Tank. Then They can fill the 5/7 of that Tank in how many minutes?
a)
45 Minutes
b)
49 Minutes
c)
63 Minutes
d)
81 Minutes
e)
None
|
|
Aarav Sharma answered |
Time taken by two pipes to fill full Tank is = √ab min = 63 min
5/7 Tank = 63*5/7 = 45 min
Three pipes A, B, and C can fill the tank in 10 hours, 20 hours and 40 hours respectively. In the beginning all of them are opened simultaneously. After 2 hours, tap C is closed and A and B are kept running. After the 4th hour, tap B is also closed. The remaining work is done by tap A alone. What is the percentage of the work done by tap A alone?- a)30 %
- b)35 %
- c)45 %
- d)50 %
- e)None of the Above
Correct answer is option 'B'. Can you explain this answer?
Three pipes A, B, and C can fill the tank in 10 hours, 20 hours and 40 hours respectively. In the beginning all of them are opened simultaneously. After 2 hours, tap C is closed and A and B are kept running. After the 4th hour, tap B is also closed. The remaining work is done by tap A alone. What is the percentage of the work done by tap A alone?
a)
30 %
b)
35 %
c)
45 %
d)
50 %
e)
None of the Above

|
Future Foundation Institute answered |
Pipe A’s work in % = 100/10 = 10%
Pipe B’s work in % = 100/20 = 5%
Pipe C’s work in % = 100/40 = 2.5%
All of them are opened for 2 hours + after 2 hours, tap C is closed + After the 4th hour, tap B is also closed = 100
⇒ (10+5+2.5)*2 + (10+5)*2 + X = 100
⇒ 35 + 30 + work by tap A alone = 100
⇒ work by tap A alone = 100-65 = 35%
Pipe B’s work in % = 100/20 = 5%
Pipe C’s work in % = 100/40 = 2.5%
All of them are opened for 2 hours + after 2 hours, tap C is closed + After the 4th hour, tap B is also closed = 100
⇒ (10+5+2.5)*2 + (10+5)*2 + X = 100
⇒ 35 + 30 + work by tap A alone = 100
⇒ work by tap A alone = 100-65 = 35%
There are 4 filling pipes and 3 emptying pipes capable of filling and emptying in 12 minutes and 15 minutes respectively. If all the pipes are opened together and as a result they fill 10 litres of water per minute. Find the capacity of the tank.- a)65ltr
- b)70ltr
- c)75ltr
- d)80ltr
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
There are 4 filling pipes and 3 emptying pipes capable of filling and emptying in 12 minutes and 15 minutes respectively. If all the pipes are opened together and as a result they fill 10 litres of water per minute. Find the capacity of the tank.
a)
65ltr
b)
70ltr
c)
75ltr
d)
80ltr
e)
None of these
|
|
Aisha Gupta answered |
(4/12 – 3/15)*t = 1
t = 15/2 minute – in this time the tank will be filled. So the capacity = (15/2)*10 = 75 litre
t = 15/2 minute – in this time the tank will be filled. So the capacity = (15/2)*10 = 75 litre
Two pipes P and Q can fill a tank in 10 min and 12 min respectively and a waste pipe can carry off 12 litres of water per minute. If all the pipes are opened when the tank is full and it takes one hour to empty the tank. Find the capacity of the tank.- a)30
- b)45
- c)60
- d)75
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
Two pipes P and Q can fill a tank in 10 min and 12 min respectively and a waste pipe can carry off 12 litres of water per minute. If all the pipes are opened when the tank is full and it takes one hour to empty the tank. Find the capacity of the tank.
a)
30
b)
45
c)
60
d)
75
e)
None of these
|
|
Aarav Sharma answered |
Problem:
Two pipes P and Q can fill a tank in 10 min and 12 min respectively and a waste pipe can carry off 12 litres of water per minute. If all the pipes are opened when the tank is full and it takes one hour to empty the tank. Find the capacity of the tank.
Solution:
Let the capacity of the tank be 'x' litres.
Given, Pipe P can fill the tank in 10 minutes. So, the amount of water it can fill in 1 minute is x/10 litres.
Similarly, Pipe Q can fill the tank in 12 minutes. So, the amount of water it can fill in 1 minute is x/12 litres.
The waste pipe can carry off 12 litres of water per minute. So, the net amount of water filled in 1 minute when all pipes are opened is (x/10 + x/12 - 12) litres.
It takes 1 hour to empty the tank. So, the amount of water emptied in 1 minute is x/60 litres.
Therefore, the net amount of water filled in 1 minute is equal to the amount of water emptied in 1 minute. Hence, we can write the equation as follows:
x/10 + x/12 - 12 = x/60
Solving this equation, we get x = 60 litres.
Answer:
The capacity of the tank is 60 litres. Therefore, the correct answer is option (c).
Two pipes P and Q can fill a tank in 10 min and 12 min respectively and a waste pipe can carry off 12 litres of water per minute. If all the pipes are opened when the tank is full and it takes one hour to empty the tank. Find the capacity of the tank.
Solution:
Let the capacity of the tank be 'x' litres.
Given, Pipe P can fill the tank in 10 minutes. So, the amount of water it can fill in 1 minute is x/10 litres.
Similarly, Pipe Q can fill the tank in 12 minutes. So, the amount of water it can fill in 1 minute is x/12 litres.
The waste pipe can carry off 12 litres of water per minute. So, the net amount of water filled in 1 minute when all pipes are opened is (x/10 + x/12 - 12) litres.
It takes 1 hour to empty the tank. So, the amount of water emptied in 1 minute is x/60 litres.
Therefore, the net amount of water filled in 1 minute is equal to the amount of water emptied in 1 minute. Hence, we can write the equation as follows:
x/10 + x/12 - 12 = x/60
Solving this equation, we get x = 60 litres.
Answer:
The capacity of the tank is 60 litres. Therefore, the correct answer is option (c).
Two taps can separately fill the tank in 10m and 15min respectively. They fill the tank in 12 minutes when a third pipe which empties the tank is also opened. What is the time taken by the third pipe to empty the whole tank?- a)14 minutes
- b)15 minutes
- c)12 minutes
- d)20 minutes
- e)16 minutes
Correct answer is option 'C'. Can you explain this answer?
Two taps can separately fill the tank in 10m and 15min respectively. They fill the tank in 12 minutes when a third pipe which empties the tank is also opened. What is the time taken by the third pipe to empty the whole tank?
a)
14 minutes
b)
15 minutes
c)
12 minutes
d)
20 minutes
e)
16 minutes

|
Target Study Academy answered |
1/10 + 1/15 – 1/x = 1/12
Solve, x = 12
Solve, x = 12
Two pipes A and B can fill a tank in 20 and 30 minutes respectively. Both the pipes are opened together but after 5 minutes pipe B is closed. What is the total time required to fill the tank- a)16.1/3 min
- b)16.2/3 min
- c)17.2/3 min
- d)18.2/3 min
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
Two pipes A and B can fill a tank in 20 and 30 minutes respectively. Both the pipes are opened together but after 5 minutes pipe B is closed. What is the total time required to fill the tank
a)
16.1/3 min
b)
16.2/3 min
c)
17.2/3 min
d)
18.2/3 min
e)
None of these

|
Future Foundation Institute answered |
(1/20 + 1/30)*5 + (1/20)*T = 1
total time = T + 5 min
total time = T + 5 min
Three pipes A, B and C is attached to a cistern. A can fill it in 20 minutes and B can fill it in 30 minutes. C is a waste pipe. After opening both the pipes A and B, Riya leaves the cistern to fill and returns when the cistern is supposed to be filled. But she found that waste pipe C had been left open, she closes it and now the cistern takes 5 minutes more to fill. In how much time the pipe C can empty the full cistern?- a)26.8 minutes
- b)25.8 minutes
- c)27.8 minutes
- d)28.8 minutes
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
Three pipes A, B and C is attached to a cistern. A can fill it in 20 minutes and B can fill it in 30 minutes. C is a waste pipe. After opening both the pipes A and B, Riya leaves the cistern to fill and returns when the cistern is supposed to be filled. But she found that waste pipe C had been left open, she closes it and now the cistern takes 5 minutes more to fill. In how much time the pipe C can empty the full cistern?
a)
26.8 minutes
b)
25.8 minutes
c)
27.8 minutes
d)
28.8 minutes
e)
None of these
|
|
Preeti Khanna answered |
The tank supposed to be filled in (30*20)/50 = 12 minutes
so, (1/20 + 1/30)*12 – 12/C + (1/20 + 1/30)*5 = 1 (A and B work for 12 minutes and also C work for 12 minutes and then A and B takes 5 more minutes to fill the tank)
solve for C, we will get C = 144/5 = 28.8
so, (1/20 + 1/30)*12 – 12/C + (1/20 + 1/30)*5 = 1 (A and B work for 12 minutes and also C work for 12 minutes and then A and B takes 5 more minutes to fill the tank)
solve for C, we will get C = 144/5 = 28.8
A Tank is filled with the mixture of Milk and Water in the ratio of 3:2 up to 2/5 of its capacity. The tank has two inlet pipes i.e., Milk and Water inlets. Milk and Water pipe can fill an empty tank in 12 and 18 hours respectively. Now both pipes are opened simultaneously and closed after the Tank is completely filled, then what is the ratio of Milk and Water in the full Tank if it can accommodate 250Litre?- a)1:1
- b)2:3
- c)3:2
- d)5:4
- e)None
Correct answer is option 'C'. Can you explain this answer?
A Tank is filled with the mixture of Milk and Water in the ratio of 3:2 up to 2/5 of its capacity. The tank has two inlet pipes i.e., Milk and Water inlets. Milk and Water pipe can fill an empty tank in 12 and 18 hours respectively. Now both pipes are opened simultaneously and closed after the Tank is completely filled, then what is the ratio of Milk and Water in the full Tank if it can accommodate 250Litre?
a)
1:1
b)
2:3
c)
3:2
d)
5:4
e)
None

|
Machine Experts answered |
Initial Milk = 2/5*250*3/5 = 60 L
Water = 2/5*250*2/5 = 40 L
Rest of Tank =150 L
Pipes are opened then can fill rest of tank in 108/25 hours
H/W = constant
then (108/25)/12/x = (108/25)/18(150-x)
X = 90 = Milk, Water = 60
Final ratio = 3:2
Water = 2/5*250*2/5 = 40 L
Rest of Tank =150 L
Pipes are opened then can fill rest of tank in 108/25 hours
H/W = constant
then (108/25)/12/x = (108/25)/18(150-x)
X = 90 = Milk, Water = 60
Final ratio = 3:2
A Special pump can be used for filling as well as for emptying a Cistern. The capacity of the Cistern is 2400m³. The emptying capacity of the Cistern is 10m³ per minute higher than its filling capacity and the pump needs 8 minutes lesser to Cistern the tank than it needs to fill it. What is the filling capacity of the pump?- a)40m³/min
- b)50m³/min
- c)60m³/min
- d)30m³/min
- e)None of the Above
Correct answer is option 'B'. Can you explain this answer?
A Special pump can be used for filling as well as for emptying a Cistern. The capacity of the Cistern is 2400m³. The emptying capacity of the Cistern is 10m³ per minute higher than its filling capacity and the pump needs 8 minutes lesser to Cistern the tank than it needs to fill it. What is the filling capacity of the pump?
a)
40m³/min
b)
50m³/min
c)
60m³/min
d)
30m³/min
e)
None of the Above

|
Cstoppers Instructors answered |
Filling Capacity of the Pump = x m/min
Emptying Capacity of the pump = (x+10) m/min
2400/x – 2400/x+10 = 8
(x – 50) + (x + 60) = 0
x = 50
Emptying Capacity of the pump = (x+10) m/min
2400/x – 2400/x+10 = 8
(x – 50) + (x + 60) = 0
x = 50
10 buckets of water fill a taken when the capacity of each bucked is 14 liter. How many buckets will be needed to fill the same tank, if the capacity of each bucket is 7litres ?- a)10
- b)12
- c)18
- d)20
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
10 buckets of water fill a taken when the capacity of each bucked is 14 liter. How many buckets will be needed to fill the same tank, if the capacity of each bucket is 7litres ?
a)
10
b)
12
c)
18
d)
20
e)
None of these
|
|
Anaya Patel answered |
10*14 = x*7
X = 10*14/7 = 20
X = 10*14/7 = 20
In a tank there is a pipe which can be used for filling the tank as well as for emptying it. The capacity of the tank is 1200 m³. The emptying of the tank is 10 m³ per minute higher than its filling capacity and the pump needs 6 minutes lesser to empty the tank than it needs to fill it. What is the filling capacity of the pipe?- a)20 m³ / min.
- b)40 m³ / min.
- c)50 m³ / min.
- d)60 m³ / min.
- e)None of the Above
Correct answer is option 'B'. Can you explain this answer?
In a tank there is a pipe which can be used for filling the tank as well as for emptying it. The capacity of the tank is 1200 m³. The emptying of the tank is 10 m³ per minute higher than its filling capacity and the pump needs 6 minutes lesser to empty the tank than it needs to fill it. What is the filling capacity of the pipe?
a)
20 m³ / min.
b)
40 m³ / min.
c)
50 m³ / min.
d)
60 m³ / min.
e)
None of the Above
|
|
Anaya Patel answered |
1200/x – 1200/(x+10) = 6
200/x – 200/(x+10) = 6
x2 + 10x – 2000 = 0
x = 40
200/x – 200/(x+10) = 6
x2 + 10x – 2000 = 0
x = 40
A Cistern has an inlet pipe and outlet pipe. The inlet pipe fills the cistern completely in 1 hour 20 minutes when the outlet pipe is plugged. The outlet pipe empties the tank completely in 6 hours when the inlet pipe is plugged. If there is a leakage also which is capable of draining out the water from the tank at half of the rate of the outlet pipe, then what is the time taken to fill the empty tank when both the pipes are opened?- a)3 hours
- b)2 hours
- c)5 hours
- d)4 hours
- e)None of the Above
Correct answer is option 'B'. Can you explain this answer?
A Cistern has an inlet pipe and outlet pipe. The inlet pipe fills the cistern completely in 1 hour 20 minutes when the outlet pipe is plugged. The outlet pipe empties the tank completely in 6 hours when the inlet pipe is plugged. If there is a leakage also which is capable of draining out the water from the tank at half of the rate of the outlet pipe, then what is the time taken to fill the empty tank when both the pipes are opened?
a)
3 hours
b)
2 hours
c)
5 hours
d)
4 hours
e)
None of the Above
|
|
Aryan Khanna answered |
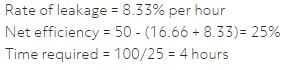
Two pipes A and B can alone fill a tank in 20 minutes and 30 minutes respectively. But due to a leak at the bottom of tank, it took 3 more minutes to fill the tank. In how many hours, the leak can alone empty the full tank?- a)60
- b)30
- c)48
- d)56
- e)72
Correct answer is option 'A'. Can you explain this answer?
Two pipes A and B can alone fill a tank in 20 minutes and 30 minutes respectively. But due to a leak at the bottom of tank, it took 3 more minutes to fill the tank. In how many hours, the leak can alone empty the full tank?
a)
60
b)
30
c)
48
d)
56
e)
72

|
Divey Sethi answered |
A and B can fill tank in (1/20 + 1/30) = 1/12 so 12 minutes
But it took 3 more minutes, this means the tank got full in 12+3 = 15 minutes
So (1/20 + 1/30 – 1/x) = 1/15
Solve, x = 60
But it took 3 more minutes, this means the tank got full in 12+3 = 15 minutes
So (1/20 + 1/30 – 1/x) = 1/15
Solve, x = 60
Three pipe P, Q and R can fill a tank in 12 minutes, 18 minutes and 24 minutes respectively. The pipe R is closed 12 minutes before the tank is filled. In what time the tank is full?- a)8.(5/13) hrs
- b)8.(4/13) hrs
- c)7.(4/13) hrs
- d)8.(6/13) hrs
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
Three pipe P, Q and R can fill a tank in 12 minutes, 18 minutes and 24 minutes respectively. The pipe R is closed 12 minutes before the tank is filled. In what time the tank is full?
a)
8.(5/13) hrs
b)
8.(4/13) hrs
c)
7.(4/13) hrs
d)
8.(6/13) hrs
e)
None of these
|
|
Aisha Gupta answered |
Let T is the time taken by the pipes to fill the tank
(1/12 + 1/18 + 1/24)*(T – 12) + (1/12 + 1/18)*12 = 1
We will get T = 108/13 = 8.(4/13) hrs
(1/12 + 1/18 + 1/24)*(T – 12) + (1/12 + 1/18)*12 = 1
We will get T = 108/13 = 8.(4/13) hrs
Pipe A can fill a Tank in 18 Hours, Pipe B can empty a Tank in 12 Hours, Pipe C can fill Tank in 6 Hours. The Tank is already filled up to 1/6 of its capacity. Now Pipe A is opened in the First Hour alone, Pipe B is opened in the Second Hour alone and Pipe C is opened in the Third Hour alone. This cycle is repeated until the Tank gets filled. Then in How many Hours does the rest of Tank gets filled?- a)15 Hours
- b)18 Hours
- c)20 Hours
- d)24 Hours
- e)None
Correct answer is option 'B'. Can you explain this answer?
Pipe A can fill a Tank in 18 Hours, Pipe B can empty a Tank in 12 Hours, Pipe C can fill Tank in 6 Hours. The Tank is already filled up to 1/6 of its capacity. Now Pipe A is opened in the First Hour alone, Pipe B is opened in the Second Hour alone and Pipe C is opened in the Third Hour alone. This cycle is repeated until the Tank gets filled. Then in How many Hours does the rest of Tank gets filled?
a)
15 Hours
b)
18 Hours
c)
20 Hours
d)
24 Hours
e)
None
|
|
Kavya Saxena answered |
In First Hour Tank filled = 1/6+1/18
Second Hour = 1/6+1/18-1/12
Third Hour = 1/6+1/18-1/12+1/6 = 11/36 is filled 25/36 is left
From then 3 hours work = 1/18-1/12+1/6 = 5/36
5*3 Hours = 5*5/36 = 25/36
Total = 5*3+3 = 18 Hours
Second Hour = 1/6+1/18-1/12
Third Hour = 1/6+1/18-1/12+1/6 = 11/36 is filled 25/36 is left
From then 3 hours work = 1/18-1/12+1/6 = 5/36
5*3 Hours = 5*5/36 = 25/36
Total = 5*3+3 = 18 Hours
Pipe A and B can fill a Tank alone in 48 Hours and 24 Hours respectively. Another Pipe C can empty the same Tank alone in 36 Hours. In an empty Tank for the First hour, Pipe A is opened alone, Second Hour pipe B is opened alone, Third Hour pipe C is opened alone. This process is continued until the Tank is filled. Then Pipe B is opened for How many Hours?- a)28 Hours
- b)28 Hours 10 Min
- c)29 Hours
- d)29 Hours 10 Min
- e)None
Correct answer is option 'B'. Can you explain this answer?
Pipe A and B can fill a Tank alone in 48 Hours and 24 Hours respectively. Another Pipe C can empty the same Tank alone in 36 Hours. In an empty Tank for the First hour, Pipe A is opened alone, Second Hour pipe B is opened alone, Third Hour pipe C is opened alone. This process is continued until the Tank is filled. Then Pipe B is opened for How many Hours?
a)
28 Hours
b)
28 Hours 10 Min
c)
29 Hours
d)
29 Hours 10 Min
e)
None
|
|
Aarav Sharma answered |
Given:
Pipe A fills the tank alone in 48 hours.
Pipe B fills the tank alone in 24 hours.
Pipe C empties the tank alone in 36 hours.
In the first hour, only Pipe A is opened, so it fills 1/48th of the tank.
In the second hour, only Pipe B is opened, so it fills 1/24th of the tank.
In the third hour, only Pipe C is opened, so it empties 1/36th of the tank.
We can observe that in the first three hours, the net amount of water filled in the tank is:
1/48 - 1/24 - 1/36 = (1/48) - (2/48) - (3/48) = -4/48 = -1/12
Since the tank is initially empty, the net amount of water in the tank after the first three hours is negative, which means the tank is not filled yet.
Let's assume that after x hours, the tank is filled. We can write the equation as:
(x/48) - (x/24) - (x/36) = 1
Simplifying the equation, we get:
(3x - 6x - 4x) / (48 * 24 * 36) = 1
-7x / (48 * 24 * 36) = 1
Solving for x, we get:
x = -48 * 24 * 36 / 7
Since x represents the number of hours, it cannot be negative. Therefore, we can ignore the negative sign and calculate the value of x as:
x = 48 * 24 * 36 / 7 = 82971.4286 hours
Since x represents the number of hours, it cannot be in decimal form. Therefore, we round it up to the nearest whole number, which is 82972 hours.
To find the number of hours Pipe B is opened, we subtract the first three hours from the total time:
82972 - 3 = 82969 hours
Therefore, Pipe B is opened for 82969 hours, which is equivalent to 28 hours and 10 minutes.
Hence, the correct answer is option B) 28 hours 10 minutes.
Pipe A fills the tank alone in 48 hours.
Pipe B fills the tank alone in 24 hours.
Pipe C empties the tank alone in 36 hours.
In the first hour, only Pipe A is opened, so it fills 1/48th of the tank.
In the second hour, only Pipe B is opened, so it fills 1/24th of the tank.
In the third hour, only Pipe C is opened, so it empties 1/36th of the tank.
We can observe that in the first three hours, the net amount of water filled in the tank is:
1/48 - 1/24 - 1/36 = (1/48) - (2/48) - (3/48) = -4/48 = -1/12
Since the tank is initially empty, the net amount of water in the tank after the first three hours is negative, which means the tank is not filled yet.
Let's assume that after x hours, the tank is filled. We can write the equation as:
(x/48) - (x/24) - (x/36) = 1
Simplifying the equation, we get:
(3x - 6x - 4x) / (48 * 24 * 36) = 1
-7x / (48 * 24 * 36) = 1
Solving for x, we get:
x = -48 * 24 * 36 / 7
Since x represents the number of hours, it cannot be negative. Therefore, we can ignore the negative sign and calculate the value of x as:
x = 48 * 24 * 36 / 7 = 82971.4286 hours
Since x represents the number of hours, it cannot be in decimal form. Therefore, we round it up to the nearest whole number, which is 82972 hours.
To find the number of hours Pipe B is opened, we subtract the first three hours from the total time:
82972 - 3 = 82969 hours
Therefore, Pipe B is opened for 82969 hours, which is equivalent to 28 hours and 10 minutes.
Hence, the correct answer is option B) 28 hours 10 minutes.
A and B are pipes such that A can empty the tank in 60 minutes and B can fill in 30 minutes. The tank is full of water and pipe A is opened. If after 18 minutes, pipe B is also opened, then in how much total time the tank will be full again?- a)32 minutes
- b)29 minutes
- c)36 minutes
- d)23 minutes
- e)18 minutes
Correct answer is option 'C'. Can you explain this answer?
A and B are pipes such that A can empty the tank in 60 minutes and B can fill in 30 minutes. The tank is full of water and pipe A is opened. If after 18 minutes, pipe B is also opened, then in how much total time the tank will be full again?
a)
32 minutes
b)
29 minutes
c)
36 minutes
d)
23 minutes
e)
18 minutes

|
Cstoppers Instructors answered |
Emptying pipe A is opened first for 18 minutes, so in 18 minutes the part of tank it has emptied is (1/60)*18 = 9/30
Now filling pipe is also opened, now since only 9/30 of the tank is empty so 9/30 is only to be filled by both pipes, let it take now x minutes, so
(1/30 – 1/60)*x = 9/30
Solve, x= 18
So total = 18+18 = 36 minutes [total time is asked – 18 minutes when emptyimh pipe was only opened, 18 minutes when both were operating.]
Now filling pipe is also opened, now since only 9/30 of the tank is empty so 9/30 is only to be filled by both pipes, let it take now x minutes, so
(1/30 – 1/60)*x = 9/30
Solve, x= 18
So total = 18+18 = 36 minutes [total time is asked – 18 minutes when emptyimh pipe was only opened, 18 minutes when both were operating.]
A pipe can empty a tank in 60 minutes alone. Another pipe whose diameter is twice the diameter of first pipe is also opened. Now find the time in which both pipe will empty the tank together.- a)8 min
- b)10 min
- c)12 min
- d)14 min
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
A pipe can empty a tank in 60 minutes alone. Another pipe whose diameter is twice the diameter of first pipe is also opened. Now find the time in which both pipe will empty the tank together.
a)
8 min
b)
10 min
c)
12 min
d)
14 min
e)
None of these
|
|
Kavya Saxena answered |

Two pipes P and Q can fill a cistern in 12 hours and 4 hours respectively. If they are opened on alternate hours and if pipe A is opened first, in how many hours will the tank be full?- a)4 hours
- b)5 hours
- c)2 hours
- d)6 hours
- e)None of the Above
Correct answer is option 'D'. Can you explain this answer?
Two pipes P and Q can fill a cistern in 12 hours and 4 hours respectively. If they are opened on alternate hours and if pipe A is opened first, in how many hours will the tank be full?
a)
4 hours
b)
5 hours
c)
2 hours
d)
6 hours
e)
None of the Above

|
Future Foundation Institute answered |
Pipe P can fill = 1/12
Pipe Q can fill = 1/4
For every two hour, 1/12 + 1/4 = 1/3 Part filled
Total = 6 hours
Pipe Q can fill = 1/4
For every two hour, 1/12 + 1/4 = 1/3 Part filled
Total = 6 hours
Three pipes A, B and C can fill the cistern in 10, 12, and 15 hours respectively. In how much time the cistern will be full if A is operated for the whole time and B and C are operated alternately which B being first?- a)10 hours 32 minutes
- b)6 hours
- c)
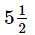 hours
hours - d)
 hours
hours - e)
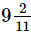 hours
hours
Correct answer is option 'D'. Can you explain this answer?
Three pipes A, B and C can fill the cistern in 10, 12, and 15 hours respectively. In how much time the cistern will be full if A is operated for the whole time and B and C are operated alternately which B being first?
a)
10 hours 32 minutes
b)
6 hours
c)
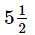 hours
hoursd)
 hours
hourse)
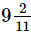 hours
hours|
|
Rhea Reddy answered |
In first hour, part of cistern filled is (1/10 + 1/12) = 11/60
In second hour, part of cistern filled is (1/10 + 1/15) = 1/6
So in 2 hours, part of cistern filled is 11/60 + 10/60 = 21/60 = 7/20
now in 2*2 (4) hours, part of cistern filled is (7/20)*2 = 14/20 = 7/10
now in the 5th hour, A+B’s turn which fill 11/60 in that hour, but the cistern remaining to be filled is (1 – 7/10) = 3/10, since 3/10 is more than 11/60, so after 5th hour remaining part to be filled is 3/10 – 11/60 = 7/60
now in 6th hour, (A+C)’s turn, it will fill remaining 7/60 in (7/60)*(6/1) = 7/10 so total 5 7/10 hours
In second hour, part of cistern filled is (1/10 + 1/15) = 1/6
So in 2 hours, part of cistern filled is 11/60 + 10/60 = 21/60 = 7/20
now in 2*2 (4) hours, part of cistern filled is (7/20)*2 = 14/20 = 7/10
now in the 5th hour, A+B’s turn which fill 11/60 in that hour, but the cistern remaining to be filled is (1 – 7/10) = 3/10, since 3/10 is more than 11/60, so after 5th hour remaining part to be filled is 3/10 – 11/60 = 7/60
now in 6th hour, (A+C)’s turn, it will fill remaining 7/60 in (7/60)*(6/1) = 7/10 so total 5 7/10 hours
Two pipes P and Q are opened together to fill a tank. Both the pipes fill the tank in time “x” If Q separately took 25 minutes more time than “x” to fill the tank and Q took 49 minutes more time than “x” to fill the tank, then find out the value of x?- a)48 minutes
- b)35 minutes
- c)54 minutes
- d)68 minutes
- e)None of the Above
Correct answer is option 'B'. Can you explain this answer?
Two pipes P and Q are opened together to fill a tank. Both the pipes fill the tank in time “x” If Q separately took 25 minutes more time than “x” to fill the tank and Q took 49 minutes more time than “x” to fill the tank, then find out the value of x?
a)
48 minutes
b)
35 minutes
c)
54 minutes
d)
68 minutes
e)
None of the Above
|
|
Preeti Khanna answered |
Time is taken to fill the tank by both Pipes x = √a*b
x = √25*49 = 5 * 7 = 35
x = √25*49 = 5 * 7 = 35
Two Pipes A and B together can fill a Tank in ‘X’ minutes. If ‘A’ is Inlet Pipe can Fill the Tank alone in 40 minutes less than ‘X’ minutes and ‘B’ is Outlet pipe can empty the Tank alone in 30 minutes less than ‘X’ minutes. Then together they can fill the empty Tank in how many minutes?- a)48 Minutes
- b)54 Minutes
- c)60 Minutes
- d)70 Minutes
- e)None
Correct answer is option 'C'. Can you explain this answer?
Two Pipes A and B together can fill a Tank in ‘X’ minutes. If ‘A’ is Inlet Pipe can Fill the Tank alone in 40 minutes less than ‘X’ minutes and ‘B’ is Outlet pipe can empty the Tank alone in 30 minutes less than ‘X’ minutes. Then together they can fill the empty Tank in how many minutes?
a)
48 Minutes
b)
54 Minutes
c)
60 Minutes
d)
70 Minutes
e)
None

|
Divey Sethi answered |
1/x-40 – 1/x-30 = 1/x
x = 60 min
x = 60 min
Three pipes P, Q and R can fill the tank in 5, 10 and 15 minutes respectively. If all the pipes are opened together and pipe Q is turned off 5 minutes before the tank is fill. Then find the time in which the tank will full.- a)45/11hrs
- b)53/11hrs
- c)51/13hrs
- d)47/11hrs
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
Three pipes P, Q and R can fill the tank in 5, 10 and 15 minutes respectively. If all the pipes are opened together and pipe Q is turned off 5 minutes before the tank is fill. Then find the time in which the tank will full.
a)
45/11hrs
b)
53/11hrs
c)
51/13hrs
d)
47/11hrs
e)
None of these
|
|
Kavya Saxena answered |
Let total time taken by the pipes is T hrs, then
(1/5 + 1/10 + 1/15)*(T – 5) + (1/5 + 1/15)*5 = 1
(1/5 + 1/10 + 1/15)*(T – 5) + (1/5 + 1/15)*5 = 1
Three pipes A, B and C can fill a cistern in 6 hours. After working at it together for 2 hours, C is closed and A and B can fill the remaining part in 6 hours. The number of hours taken by C alone to fill the cistern is- a)12hrs
- b)10hrs
- c)18hrs
- d)8hrs
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
Three pipes A, B and C can fill a cistern in 6 hours. After working at it together for 2 hours, C is closed and A and B can fill the remaining part in 6 hours. The number of hours taken by C alone to fill the cistern is
a)
12hrs
b)
10hrs
c)
18hrs
d)
8hrs
e)
None of these

|
Cstoppers Instructors answered |
A+B+C in 1h = 1/6
A+B+C in 2h = 2/6 = 1/3
Remaining = 1-1/3 = 2/3
A+B in 6hrs = 2/3
A+B in 1hr = 2/18
C alone to fill the cistern = 1/6 – 2/18 = 3-2/18 = 1/18
A+B+C in 2h = 2/6 = 1/3
Remaining = 1-1/3 = 2/3
A+B in 6hrs = 2/3
A+B in 1hr = 2/18
C alone to fill the cistern = 1/6 – 2/18 = 3-2/18 = 1/18
If a pipe A can fill a tank 3 times faster than pipe B. If both the pipes can fill the tank in 42 minutes, then the slower pipe alone will be able to fill the tank in?- a)148 minutes
- b)124 minutes
- c)154 minutes
- d)168 minutes
- e)None of the Above
Correct answer is option 'D'. Can you explain this answer?
If a pipe A can fill a tank 3 times faster than pipe B. If both the pipes can fill the tank in 42 minutes, then the slower pipe alone will be able to fill the tank in?
a)
148 minutes
b)
124 minutes
c)
154 minutes
d)
168 minutes
e)
None of the Above

|
Cstoppers Instructors answered |
Time is taken by pipe A = x
Time is taken by pipe B = x/3
1/x + 3/x = 1/42
x = 168 minutes
Time is taken by pipe B = x/3
1/x + 3/x = 1/42
x = 168 minutes
Pipes P and Q can fill the tank in 24 minutes and 32 minutes respectively. Both piped are opened together. To have the tank full in 18 minutes, after how many minutes the pipe P must be closed?- a)22 minutes
- b)21 minutes
- c)15 minutes
- d)12.5 minutes
- e)10.5 minutes
Correct answer is option 'E'. Can you explain this answer?
Pipes P and Q can fill the tank in 24 minutes and 32 minutes respectively. Both piped are opened together. To have the tank full in 18 minutes, after how many minutes the pipe P must be closed?
a)
22 minutes
b)
21 minutes
c)
15 minutes
d)
12.5 minutes
e)
10.5 minutes
|
|
Aisha Gupta answered |
P is to be closed before 18 minutes, let it is closed after x minutes, then Q worked for all 18 minutes. So,
(1/24)*x + (1/32)*18 = 1
Solve, x = 10.5
(1/24)*x + (1/32)*18 = 1
Solve, x = 10.5
Two pipes P and Q can fill a tank in 20hrs and 25hrs respectively while a third pipe R can empty the tank in 30hrs. If all the pipes are opened together for 10hrs and then pipe R is closed then in what time the tank can be filled.- a)400/23hrs
- b)400/27hrs
- c)200/23hrs
- d)200/27hrs
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
Two pipes P and Q can fill a tank in 20hrs and 25hrs respectively while a third pipe R can empty the tank in 30hrs. If all the pipes are opened together for 10hrs and then pipe R is closed then in what time the tank can be filled.
a)
400/23hrs
b)
400/27hrs
c)
200/23hrs
d)
200/27hrs
e)
None of these

|
Cstoppers Instructors answered |
(1/20 + 1/25 – 1/30)*10 + (1/20 + 1/25)*x = 1
We get x = 130/27, so total time to fill the tank = 130/27 + 10 = 400/27 hrs
We get x = 130/27, so total time to fill the tank = 130/27 + 10 = 400/27 hrs
There are three taps A, B and C which can fill a tank in 12hrs, 15hrs and 30 hrs respectively. If the tap A is opened first, after one hour tap B was opened and after 2 hours from the start of A, tap C is also opened. Find the time in which the tank is full.- a)6(2/11)hr
- b)6(3/11)hr
- c)5(3/11)hr
- d)5(2/11)hr
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
There are three taps A, B and C which can fill a tank in 12hrs, 15hrs and 30 hrs respectively. If the tap A is opened first, after one hour tap B was opened and after 2 hours from the start of A, tap C is also opened. Find the time in which the tank is full.
a)
6(2/11)hr
b)
6(3/11)hr
c)
5(3/11)hr
d)
5(2/11)hr
e)
None of these
|
|
Nikita Singh answered |
In first hour only A is opened, in the next hour A and B are opened and in the third hour A, B and C are opened.
So, in three hours (3/12 + 2/15 + 1/30) = 25/60 tank is already filled.
Now, 25/60 = (1/12 + 1/15 + 1/30)*t
T = 25/11. Total time = 3 + 25/11 = 58/11 hours
So, in three hours (3/12 + 2/15 + 1/30) = 25/60 tank is already filled.
Now, 25/60 = (1/12 + 1/15 + 1/30)*t
T = 25/11. Total time = 3 + 25/11 = 58/11 hours
Two pipes A and B can fill a tank in 8 minutes and 12 minutes respectively. If both the pipes are openedsimultaneously, after what time should B be closed so that the tank is full in 6 minutes?- a)1 min
- b)2 min
- c)3 min
- d)4 min
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
Two pipes A and B can fill a tank in 8 minutes and 12 minutes respectively. If both the pipes are openedsimultaneously, after what time should B be closed so that the tank is full in 6 minutes?
a)
1 min
b)
2 min
c)
3 min
d)
4 min
e)
None of these
|
|
Aarav Sharma answered |
Problem Statement:
Two pipes A and B can fill a tank in 8 minutes and 12 minutes respectively. If both the pipes are opened simultaneously, after what time should B be closed so that the tank is full in 6 minutes?
Solution:
Let's assume that B should be closed after x minutes so that the tank is full in 6 minutes.
Therefore, the amount of work done by pipe A in 6 minutes = 6/8 = 3/4
The amount of work done by pipe B in x minutes = x/12
The total amount of work done by both pipes in 6 minutes = 1
So, the equation becomes:
3/4 + (x/12) = 1
Solving for x, we get:
x/12 = 1/4
x = 3 minutes
Therefore, B should be closed after 3 minutes so that the tank is full in 6 minutes.
Answer: Option (c) 3 min
Two pipes A and B can fill a tank in 8 minutes and 12 minutes respectively. If both the pipes are opened simultaneously, after what time should B be closed so that the tank is full in 6 minutes?
Solution:
Let's assume that B should be closed after x minutes so that the tank is full in 6 minutes.
Therefore, the amount of work done by pipe A in 6 minutes = 6/8 = 3/4
The amount of work done by pipe B in x minutes = x/12
The total amount of work done by both pipes in 6 minutes = 1
So, the equation becomes:
3/4 + (x/12) = 1
Solving for x, we get:
x/12 = 1/4
x = 3 minutes
Therefore, B should be closed after 3 minutes so that the tank is full in 6 minutes.
Answer: Option (c) 3 min
Two pipes A and B can fill a tank in 10 hours and 15 hours respectively while a third pipe C can empty the full tank in 20 hours. All the pipes are opened for 5 hours and then C is closed. Find the time in which the tank is full?- a)5.5 hrs
- b)6.5 hrs
- c)7.5 hrs
- d)8.5 hrs
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
Two pipes A and B can fill a tank in 10 hours and 15 hours respectively while a third pipe C can empty the full tank in 20 hours. All the pipes are opened for 5 hours and then C is closed. Find the time in which the tank is full?
a)
5.5 hrs
b)
6.5 hrs
c)
7.5 hrs
d)
8.5 hrs
e)
None of these
|
|
Faizan Khan answered |

A leak in the bottom of a tank can empty the full tank in 7 hours. An inlet pipe fills water at the rate of 2 litres a minute. When the tank is full the inlet is opened and due to the leak the tank is empty in 8 hours. The capacity of the tank in litres is- a)3450 litres
- b)5460 litres
- c)7620 litres
- d)6720 litres
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
A leak in the bottom of a tank can empty the full tank in 7 hours. An inlet pipe fills water at the rate of 2 litres a minute. When the tank is full the inlet is opened and due to the leak the tank is empty in 8 hours. The capacity of the tank in litres is
a)
3450 litres
b)
5460 litres
c)
7620 litres
d)
6720 litres
e)
None of these
|
|
Preeti Khanna answered |
In 1 hr = 1/7 – 1/8 = 8-7/56 = 1/56
In 1 min = 1/(56*60) = 1/3360
Inlet pipe fill water at the rate of 2 liters a minute = 2*3360 = 6720litres
In 1 min = 1/(56*60) = 1/3360
Inlet pipe fill water at the rate of 2 liters a minute = 2*3360 = 6720litres
Pipe A, B and can fill a Full Tank in 24,36 and 48 Minutes respectively. All three Pipes are Opened simultaneously in a Tank which is already filled up to 1/6 of its capacity. A and B are opened for only First 6 Minutes and closed thereafter.Then C alone filled remaining Tank. Then in total how many Minutes does C filled the Tank?- a)12 Minutes
- b)14 Minutes
- c)16 Minutes
- d)18 Minutes
- e)20 Minutes
Correct answer is option 'E'. Can you explain this answer?
Pipe A, B and can fill a Full Tank in 24,36 and 48 Minutes respectively. All three Pipes are Opened simultaneously in a Tank which is already filled up to 1/6 of its capacity. A and B are opened for only First 6 Minutes and closed thereafter.Then C alone filled remaining Tank. Then in total how many Minutes does C filled the Tank?
a)
12 Minutes
b)
14 Minutes
c)
16 Minutes
d)
18 Minutes
e)
20 Minutes

|
Divey Sethi answered |
6*(1/24+1/36+1/48) + x/48 = 5/6
x = 14 Min
C = 6+14 = 20
x = 14 Min
C = 6+14 = 20
Three pipes P, Q and R can fill a tank in 12, 15 and 20 minutes respectively. If pipe P is opened all the time and pipe Q and R are opened for one hour alternatively. The tank will be full in- a)5hr
- b)6hr
- c)7hr
- d)8hr
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
Three pipes P, Q and R can fill a tank in 12, 15 and 20 minutes respectively. If pipe P is opened all the time and pipe Q and R are opened for one hour alternatively. The tank will be full in
a)
5hr
b)
6hr
c)
7hr
d)
8hr
e)
None of these

|
Cstoppers Instructors answered |
(1/12 + 1/15) + (1/12 + 1/20) = 17/60 (in 2 hrs this much tank is filled)
so in 6 hrs 51/60 is filled. Remaining, 9/60 = (1/12 + 1/15)*t,
so T = 1hr so total = 6 + 1 = 7 hr
so in 6 hrs 51/60 is filled. Remaining, 9/60 = (1/12 + 1/15)*t,
so T = 1hr so total = 6 + 1 = 7 hr
A tap can fill a tank in 12 minutes and another tap can empty the tank in 6 minutes.If the tank is already full and then both the taps are opened the tank will be- a)Filled in 6 minutes
- b)Emptied in 6 minutes
- c)Filled in 8 minutes
- d)Emptied in 12 minutes
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
A tap can fill a tank in 12 minutes and another tap can empty the tank in 6 minutes.If the tank is already full and then both the taps are opened the tank will be
a)
Filled in 6 minutes
b)
Emptied in 6 minutes
c)
Filled in 8 minutes
d)
Emptied in 12 minutes
e)
None of these
|
|
Yash Patel answered |
1/12 – 1/6 = 1-2/12 = -1/12
Chapter doubts & questions for Pipes & Cistern - RRB JE Mock Test Series for Computer Science Engineering 2026 2025 is part of Computer Science Engineering (CSE) exam preparation. The chapters have been prepared according to the Computer Science Engineering (CSE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Computer Science Engineering (CSE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Pipes & Cistern - RRB JE Mock Test Series for Computer Science Engineering 2026 in English & Hindi are available as part of Computer Science Engineering (CSE) exam.
Download more important topics, notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily









