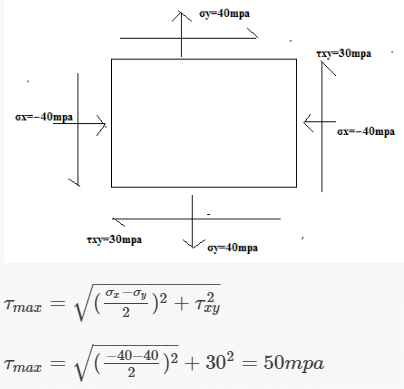
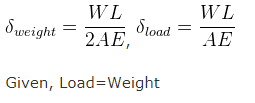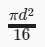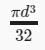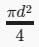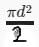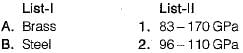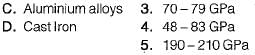All Exams >
Mechanical Engineering >
Mechanical Engineering SSC JE (Technical) >
All Questions
All questions of Strength of Materials (SOM) for Mechanical Engineering Exam
The Poisson's ratio for steel varies from
- a)0.27 to 0.30
- b)0.25 to 0.33
- c)0.31 to 0.34
- d)0.32 to 0.42
Correct answer is option 'A'. Can you explain this answer?
The Poisson's ratio for steel varies from
a)
0.27 to 0.30
b)
0.25 to 0.33
c)
0.31 to 0.34
d)
0.32 to 0.42

|
Anirban Khanna answered |
Poissons ratio. Steel - 0.23 to 0.27. Cast iron - 0.25 to 0.33. Al-0.33
When a rectangular beam is loaded transversely, the maximum tensile stress is developed on the- a)top layer
- b)bottom layer
- c)neutral axis
- d)every crosssection
Correct answer is option 'A'. Can you explain this answer?
When a rectangular beam is loaded transversely, the maximum tensile stress is developed on the
a)
top layer
b)
bottom layer
c)
neutral axis
d)
every crosssection

|
Anirban Khanna answered |
Loaded means loaded downwards. In that case upper fibres will be compressed while lower will be expanded. Hence maximum compressive stress will be developed in top layer.
Wherever some external system of forces acts on a body, it undergoes some deformation. As the body under goes some deformation, it sets up some resistance to the deformations. This resistance per unit area to deformation, is called- a)strain
- b)stress
- c)pressure
- d)modulus of elasticity
Correct answer is option 'B'. Can you explain this answer?
Wherever some external system of forces acts on a body, it undergoes some deformation. As the body under goes some deformation, it sets up some resistance to the deformations. This resistance per unit area to deformation, is called
a)
strain
b)
stress
c)
pressure
d)
modulus of elasticity

|
Sagarika Patel answered |
Body undergoes some deformation, it sets up some resistance to the deformation. This resistance per unit area to deformation, is called: Stress.
The strain energy stored in a spring, when subjected to maximum load, without suffering permanent distortion, is known as- a)impact energy
- b)proof resilience
- c)proof stress
- d)modulus of resilience
Correct answer is option 'B'. Can you explain this answer?
The strain energy stored in a spring, when subjected to maximum load, without suffering permanent distortion, is known as
a)
impact energy
b)
proof resilience
c)
proof stress
d)
modulus of resilience

|
Kaavya Sengupta answered |
Proof resilience:The maximum energy stored within the elastic limit is called proof resilience it is the strain energy corresponding to stress at elastic limit.
The relation between Young's modulus (E) and bulk modulus (K) is given by- a)
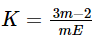
- b)
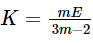
- c)
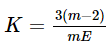
- d)
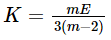
Correct answer is option 'D'. Can you explain this answer?
The relation between Young's modulus (E) and bulk modulus (K) is given by
a)
b)
c)
d)
|
|
Saikat Choudhary answered |
Relation between Young's Modulus and Bulk Modulus
Young's modulus and bulk modulus are two important parameters that describe the behavior of a solid under stress. The relation between these two parameters can be expressed mathematically as follows:
K = ρc^2
E = ρv^2
Where K is the bulk modulus, E is the Young's modulus, ρ is the density of the material, c is the speed of sound in the material, and v is the velocity of longitudinal waves in the material.
From these equations, we can derive the relation between K and E as follows:
K = ρc^2 = ρ(v^2) = ρE/(ρc^2) = (ρ/ρc^2)E
Substituting the value of ρ/ρc^2 from the equation above, we get:
K = E/[3(1-2ν)]
Where ν is the Poisson's ratio of the material, which is defined as the ratio of transverse strain to longitudinal strain.
Simplifying the equation further, we get:
K = E/[3(1-2ν)] = E/[3(1-2(0.5))] = E/[3(1-1)] = E/3
Therefore, the correct answer is option D, which states that K = E/[3(m-2)], where m = 1/ν.
Young's modulus and bulk modulus are two important parameters that describe the behavior of a solid under stress. The relation between these two parameters can be expressed mathematically as follows:
K = ρc^2
E = ρv^2
Where K is the bulk modulus, E is the Young's modulus, ρ is the density of the material, c is the speed of sound in the material, and v is the velocity of longitudinal waves in the material.
From these equations, we can derive the relation between K and E as follows:
K = ρc^2 = ρ(v^2) = ρE/(ρc^2) = (ρ/ρc^2)E
Substituting the value of ρ/ρc^2 from the equation above, we get:
K = E/[3(1-2ν)]
Where ν is the Poisson's ratio of the material, which is defined as the ratio of transverse strain to longitudinal strain.
Simplifying the equation further, we get:
K = E/[3(1-2ν)] = E/[3(1-2(0.5))] = E/[3(1-1)] = E/3
Therefore, the correct answer is option D, which states that K = E/[3(m-2)], where m = 1/ν.
The permanent mode of deformation of a material known as ____________- a)Plasticity
- b)Elasticity
- c)Slip deformation
- d)Twinning deformation
Correct answer is option 'A'. Can you explain this answer?
The permanent mode of deformation of a material known as ____________
a)
Plasticity
b)
Elasticity
c)
Slip deformation
d)
Twinning deformation
|
|
Sarita Yadav answered |
Plasticity is defined as the property of a material due to which it is permanently deformed due to loading. Elasticity is the temporary form of deformation. Twinning and Slip are mechanisms of Plastic deformation.
Which of the following is a proper sequence ?- a)proportional limit, elastic limit, yielding sequence ?
- b)elastic limit, proportional limit, yielding, failure
- c)yielding, Proportional limit, elastic limit, failure
- d)none of the above
Correct answer is option 'A'. Can you explain this answer?
Which of the following is a proper sequence ?
a)
proportional limit, elastic limit, yielding sequence ?
b)
elastic limit, proportional limit, yielding, failure
c)
yielding, Proportional limit, elastic limit, failure
d)
none of the above
|
|
Sanskriti Basu answered |
Proper Sequence of Material Behavior
The behavior of a material under load can be described by a sequence of stages. The proper sequence of material behavior is as follows:
1. Proportional limit: This is the point at which a material begins to deform elastically. Below this limit, the material will return to its original shape when the load is removed.
2. Elastic limit: This is the point beyond the proportional limit where the material will no longer return to its original shape when the load is removed. However, if the load is removed before reaching this limit, the material will still behave elastically.
3. Yielding sequence: This is the point at which the material begins to yield or deform plastically. The material will not return to its original shape when the load is removed at this point.
4. Failure: This is the point at which the material breaks or fractures.
Proper Sequence Option
The proper sequence of material behavior is given in option (a): Proportional limit, elastic limit, yielding sequence, failure. This sequence is in chronological order of how the material behaves under stress and is the correct order of material behavior.
The behavior of a material under load can be described by a sequence of stages. The proper sequence of material behavior is as follows:
1. Proportional limit: This is the point at which a material begins to deform elastically. Below this limit, the material will return to its original shape when the load is removed.
2. Elastic limit: This is the point beyond the proportional limit where the material will no longer return to its original shape when the load is removed. However, if the load is removed before reaching this limit, the material will still behave elastically.
3. Yielding sequence: This is the point at which the material begins to yield or deform plastically. The material will not return to its original shape when the load is removed at this point.
4. Failure: This is the point at which the material breaks or fractures.
Proper Sequence Option
The proper sequence of material behavior is given in option (a): Proportional limit, elastic limit, yielding sequence, failure. This sequence is in chronological order of how the material behaves under stress and is the correct order of material behavior.
Strain is defined as ratio of- a)change in volume to original volume
- b)change in length to original length.
- c)change in cross-sectional area to original cross-sectional area
- d)any one of the above
Correct answer is option 'D'. Can you explain this answer?
Strain is defined as ratio of
a)
change in volume to original volume
b)
change in length to original length.
c)
change in cross-sectional area to original cross-sectional area
d)
any one of the above
|
|
Neha Joshi answered |
The strain is defined as the ratio of change in dimension to the original dimension.
If ‘δl’ changes in the length and ‘l’ is the original length, strain = δl/l
Important Terms:
- The ratio of change in length to the original length is called the longitudinal strain.
- The ratio of change in diameter/breadth to original diameter/breadth is called the lateral strain.
- The volumetric strain of a deformed body is defined as the ratio of the change in volume of the body to the deformation to its original volume.
- Shear strain is defined as the strain accompanying a shearing action. It is the angle in radian measure through which the body gets distorted when subjected to external shearing action.
Two closely -coiled helical springs 'A' and 'B' are equal in all respects but the number of turns of spring 'A' is double that of spring 'B'. The stiffness of spring 'A' will be ....... that of spring 'B'.- a)one-half
- b)one- eighth
- c)one-fourth
- d)one-sixteenth
Correct answer is option 'A'. Can you explain this answer?
Two closely -coiled helical springs 'A' and 'B' are equal in all respects but the number of turns of spring 'A' is double that of spring 'B'. The stiffness of spring 'A' will be ....... that of spring 'B'.
a)
one-half
b)
one- eighth
c)
one-fourth
d)
one-sixteenth
|
|
Sahil Majumdar answered |
Explanation:
The stiffness of a spring is directly proportional to the number of turns of the spring. Therefore, if the number of turns of spring A is double that of spring B, then the stiffness of spring A will be twice that of spring B.
Since the two springs are equal in all other respects, such as the material, wire diameter, and mean coil diameter, the only factor affecting their stiffness is the number of turns.
Therefore, the stiffness of spring A will be one-half that of spring B.
Hence, the correct option is A.
The stiffness of a spring is directly proportional to the number of turns of the spring. Therefore, if the number of turns of spring A is double that of spring B, then the stiffness of spring A will be twice that of spring B.
Since the two springs are equal in all other respects, such as the material, wire diameter, and mean coil diameter, the only factor affecting their stiffness is the number of turns.
Therefore, the stiffness of spring A will be one-half that of spring B.
Hence, the correct option is A.
On the planes having maximum or minimum principal stresses, the tangential stress will be
- a)minimum
- b)maximum
- c)zero
- d)infinity
- e)some value depending on magnitude of two stresses
Correct answer is option 'C'. Can you explain this answer?
On the planes having maximum or minimum principal stresses, the tangential stress will be
a)
minimum
b)
maximum
c)
zero
d)
infinity
e)
some value depending on magnitude of two stresses

|
Anandu R answered |
Because the angle between the components are zero. Therefore sine of the angle between is also zero. Therefore the tangential stress is zero
The Poisson's ratio for cast iron varies from- a)0.23 to 0.27
- b)0.22 to 0.30
- c)0.31 to 0.34
- d)0.32 to 0.42
Correct answer is option 'B'. Can you explain this answer?
The Poisson's ratio for cast iron varies from
a)
0.23 to 0.27
b)
0.22 to 0.30
c)
0.31 to 0.34
d)
0.32 to 0.42
|
|
Stuti Bajaj answered |
Poisson's ratio is the ratio of the lateral strain to the longitudinal strain in a material when it is stretched or compressed.
Cast iron is a type of iron alloy that is commonly used in the manufacturing industry. It is known for its high strength, durability, and wear resistance. The Poisson's ratio of cast iron is an important mechanical property that determines its behavior under stress.
The Poisson's ratio for cast iron varies from 0.23 to 0.27. This means that when cast iron is stretched or compressed, its lateral strain is between 0.23 and 0.27 times its longitudinal strain.
Factors affecting Poisson's ratio of cast iron:
1. Composition: The composition of cast iron affects its Poisson's ratio. Different types of cast iron have different Poisson's ratios due to variations in their chemical composition.
2. Microstructure: The microstructure of cast iron also affects its Poisson's ratio. The presence of different phases and the size of the grains in the microstructure can affect the deformation behavior of the material.
3. Temperature: The temperature at which cast iron is tested can affect its Poisson's ratio. At higher temperatures, the material may exhibit different deformation behavior due to changes in the microstructure.
Importance of Poisson's ratio in engineering:
1. Design of structures: Poisson's ratio is an important parameter in the design of structures such as bridges, buildings, and aircraft. It helps engineers to predict the behavior of materials under different loading conditions.
2. Material selection: Poisson's ratio is also used to select materials for specific applications. Materials with low Poisson's ratios are preferred for applications where deformation in one direction needs to be minimized.
3. Manufacturing processes: Poisson's ratio is also used in manufacturing processes such as casting and forging. It helps to predict the deformation behavior of the material during the manufacturing process.
Cast iron is a type of iron alloy that is commonly used in the manufacturing industry. It is known for its high strength, durability, and wear resistance. The Poisson's ratio of cast iron is an important mechanical property that determines its behavior under stress.
The Poisson's ratio for cast iron varies from 0.23 to 0.27. This means that when cast iron is stretched or compressed, its lateral strain is between 0.23 and 0.27 times its longitudinal strain.
Factors affecting Poisson's ratio of cast iron:
1. Composition: The composition of cast iron affects its Poisson's ratio. Different types of cast iron have different Poisson's ratios due to variations in their chemical composition.
2. Microstructure: The microstructure of cast iron also affects its Poisson's ratio. The presence of different phases and the size of the grains in the microstructure can affect the deformation behavior of the material.
3. Temperature: The temperature at which cast iron is tested can affect its Poisson's ratio. At higher temperatures, the material may exhibit different deformation behavior due to changes in the microstructure.
Importance of Poisson's ratio in engineering:
1. Design of structures: Poisson's ratio is an important parameter in the design of structures such as bridges, buildings, and aircraft. It helps engineers to predict the behavior of materials under different loading conditions.
2. Material selection: Poisson's ratio is also used to select materials for specific applications. Materials with low Poisson's ratios are preferred for applications where deformation in one direction needs to be minimized.
3. Manufacturing processes: Poisson's ratio is also used in manufacturing processes such as casting and forging. It helps to predict the deformation behavior of the material during the manufacturing process.
Young's modulus is defined as the ratio of- a)volumetric stress and volumetric strain
- b)lateral stress and lateral strain
- c)longitudinal stress and lateral strain
- d)longitudinal stress and longitudinal strain
Correct answer is option 'D'. Can you explain this answer?
Young's modulus is defined as the ratio of
a)
volumetric stress and volumetric strain
b)
lateral stress and lateral strain
c)
longitudinal stress and lateral strain
d)
longitudinal stress and longitudinal strain

|
Megha Choudhury answered |
The linear relationship between stress and strain for a bar in simple tension or compression can be expressed by the equation
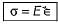
in which Eis a constant of proportionality known as modulus of elasticity for the material. The modulus of elasticity is the slope of the stress- strain diagram in the linearly elastic region and its value depends upon the particular material being used.
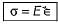
in which Eis a constant of proportionality known as modulus of elasticity for the material. The modulus of elasticity is the slope of the stress- strain diagram in the linearly elastic region and its value depends upon the particular material being used.
Two closely coiled helical springs 'A' and 'B' are equal in all respects but the diameter of wire of spring 'A' is double that of spring 'B'. The stiffness of spring 'B' will be- a)one-sixteenth
- b)one- eighth
- c)one-fourth
- d)one-half
Correct answer is option 'A'. Can you explain this answer?
Two closely coiled helical springs 'A' and 'B' are equal in all respects but the diameter of wire of spring 'A' is double that of spring 'B'. The stiffness of spring 'B' will be
a)
one-sixteenth
b)
one- eighth
c)
one-fourth
d)
one-half
|
|
Anjali Sengupta answered |
Explanation:
Stiffness of a spring is defined as the force required to produce unit displacement in the spring. Mathematically,
Stiffness (k) = F/x
where F is the force applied and x is the displacement produced.
Now, let's consider two springs A and B with the following properties:
- Both springs are equal in all respects except for the diameter of wire.
- The diameter of wire of spring A is double that of spring B.
From the above information, we can conclude that:
- The number of coils in both springs will be the same.
- The length of both springs will be the same.
- The material of both springs will be the same.
Since the diameter of wire of spring A is double that of spring B, we can write:
- The radius of wire of spring A is twice that of spring B.
- The cross-sectional area of wire of spring A is four times that of spring B.
Now, let's find the stiffness of both springs using the formula:
k = (Gd^4)/(64D^3n)
where G is the modulus of rigidity of the material, d is the diameter of wire, D is the mean diameter of the spring, and n is the number of coils.
We know that both springs have the same material, number of coils, and length. Therefore, the only variables that differ are the diameter of wire and mean diameter.
Let's assume that the mean diameter of both springs is D. Then, we can write:
- The mean diameter of spring A is D + 2r, where r is the radius of wire.
- The mean diameter of spring B is D + r.
Now, let's find the stiffness of spring A:
kA = (G(2r)^4)/(64(D+2r)^3n)
kA = (G16r^4)/(64(D+2r)^3n)
kA = (G)r^4/(4(D+2r)^3n)
Similarly, let's find the stiffness of spring B:
kB = (G(r)^4)/(64(D+r)^3n)
Now, let's compare the stiffness of both springs:
kA/kB = [(G)r^4/(4(D+2r)^3n)]/[(G(r)^4)/(64(D+r)^3n)]
kA/kB = (1/16)(D+r)^3/(D+2r)^3
kA/kB = (1/16)[(D+r)/(D+2r)]^3
Since the mean diameter of both springs is the same, we can write:
(D+r)/(D+2r) = 1 + (r/D)
Approximating this to first order, we get:
(D+r)/(D+2r) ≈ 1 + (r/D)
Substituting this in the above equation, we get:
kA/kB ≈ (1/16)(1+(r/D))^3
Since r/D is very small (since r is much smaller than D), we can approximate (1+r/D)^3 to 1+3(r/D). Therefore,
kA/kB ≈ (1/16)(1+3(r/D))
kA/kB ≈ (1/16) + (3/16)(r/D)
Since r/D is very small, we can ignore the second term and write:
k
Stiffness of a spring is defined as the force required to produce unit displacement in the spring. Mathematically,
Stiffness (k) = F/x
where F is the force applied and x is the displacement produced.
Now, let's consider two springs A and B with the following properties:
- Both springs are equal in all respects except for the diameter of wire.
- The diameter of wire of spring A is double that of spring B.
From the above information, we can conclude that:
- The number of coils in both springs will be the same.
- The length of both springs will be the same.
- The material of both springs will be the same.
Since the diameter of wire of spring A is double that of spring B, we can write:
- The radius of wire of spring A is twice that of spring B.
- The cross-sectional area of wire of spring A is four times that of spring B.
Now, let's find the stiffness of both springs using the formula:
k = (Gd^4)/(64D^3n)
where G is the modulus of rigidity of the material, d is the diameter of wire, D is the mean diameter of the spring, and n is the number of coils.
We know that both springs have the same material, number of coils, and length. Therefore, the only variables that differ are the diameter of wire and mean diameter.
Let's assume that the mean diameter of both springs is D. Then, we can write:
- The mean diameter of spring A is D + 2r, where r is the radius of wire.
- The mean diameter of spring B is D + r.
Now, let's find the stiffness of spring A:
kA = (G(2r)^4)/(64(D+2r)^3n)
kA = (G16r^4)/(64(D+2r)^3n)
kA = (G)r^4/(4(D+2r)^3n)
Similarly, let's find the stiffness of spring B:
kB = (G(r)^4)/(64(D+r)^3n)
Now, let's compare the stiffness of both springs:
kA/kB = [(G)r^4/(4(D+2r)^3n)]/[(G(r)^4)/(64(D+r)^3n)]
kA/kB = (1/16)(D+r)^3/(D+2r)^3
kA/kB = (1/16)[(D+r)/(D+2r)]^3
Since the mean diameter of both springs is the same, we can write:
(D+r)/(D+2r) = 1 + (r/D)
Approximating this to first order, we get:
(D+r)/(D+2r) ≈ 1 + (r/D)
Substituting this in the above equation, we get:
kA/kB ≈ (1/16)(1+(r/D))^3
Since r/D is very small (since r is much smaller than D), we can approximate (1+r/D)^3 to 1+3(r/D). Therefore,
kA/kB ≈ (1/16)(1+3(r/D))
kA/kB ≈ (1/16) + (3/16)(r/D)
Since r/D is very small, we can ignore the second term and write:
k
A cylindrical bar of L metres deforms by l cm. The strain in bar is- a)l/L
- b)0.1 l/L
- c)0.01 l/L
- d)100 l/L
- e)none of the above
Correct answer is option 'C'. Can you explain this answer?
A cylindrical bar of L metres deforms by l cm. The strain in bar is
a)
l/L
b)
0.1 l/L
c)
0.01 l/L
d)
100 l/L
e)
none of the above
|
|
Ayush Chawla answered |
Strain is a measure of the deformation of an object relative to its original size. It is defined as the ratio of the change in length (deformation) to the original length of the object. In this case, we have a cylindrical bar that deforms by l cm, and we need to find the strain in the bar.
To calculate the strain in the bar, we can use the formula:
Strain = (Change in length) / (Original length)
Given that the bar deforms by l cm and the original length of the bar is L metres, we can substitute these values into the formula:
Strain = l cm / L metres
However, we need to ensure that the units are consistent. Since the original length is given in metres, we need to convert the deformation from centimeters to metres:
l cm = (l cm / 100) metres
Substituting this into the formula, we get:
Strain = (l cm / 100) metres / L metres
Simplifying the expression, we find:
Strain = l / (100 * L)
This is equivalent to:
Strain = 0.01 * (l / L)
Therefore, the strain in the bar is 0.01 times the ratio of the deformation to the original length.
Hence, the correct answer is option C: 0.01 l/L.
To calculate the strain in the bar, we can use the formula:
Strain = (Change in length) / (Original length)
Given that the bar deforms by l cm and the original length of the bar is L metres, we can substitute these values into the formula:
Strain = l cm / L metres
However, we need to ensure that the units are consistent. Since the original length is given in metres, we need to convert the deformation from centimeters to metres:
l cm = (l cm / 100) metres
Substituting this into the formula, we get:
Strain = (l cm / 100) metres / L metres
Simplifying the expression, we find:
Strain = l / (100 * L)
This is equivalent to:
Strain = 0.01 * (l / L)
Therefore, the strain in the bar is 0.01 times the ratio of the deformation to the original length.
Hence, the correct answer is option C: 0.01 l/L.
Modular ratio of the two materials is the ratio of- a)linear stress to linear strain
- b)shear stress to shear strain
- c)their modulus of elasticities
- d)their modulus of rigidities
Correct answer is option 'C'. Can you explain this answer?
Modular ratio of the two materials is the ratio of
a)
linear stress to linear strain
b)
shear stress to shear strain
c)
their modulus of elasticities
d)
their modulus of rigidities

|
Shivam Sharma answered |
Modular ratio is the ratio of Youngs Modulii of Elasticity of two different materials in constructin by composite materials.e.g. in a composite bar consisting of two different materials, one having Young's modulus E1 and other having Young's modulus E2, then modular ratio is given by E1/E2.
A cube subjected to three mutually perpendicular stress of equal intensity p expenses a volumetric strain- a)3p/ E × (2/m - 1)
- b)3p/ E × (2 - m)
- c)3p/ E × (1 - 2/m)
- d)E/ 3p × (2/m - 1)
Correct answer is option 'C'. Can you explain this answer?
A cube subjected to three mutually perpendicular stress of equal intensity p expenses a volumetric strain
a)
3p/ E × (2/m - 1)
b)
3p/ E × (2 - m)
c)
3p/ E × (1 - 2/m)
d)
E/ 3p × (2/m - 1)
|
|
Neha Choudhury answered |
Stress p in x-direction causes tensile strain p/E in x-direction, while the ‘p’ in ‘y’ and ‘z’ direction causes compressive strains μ(p/E) in x-direction.
Therefore, ex = p/E - μ(p/E) - μ(p/E) = p/E x (1- 2μ)
So, ey =p/E x (1- 2μ),
ez = p/E x (1- 2μ)
Therefore, Volumetric Strain, ev = ex + ey + ez = 3p/E x (1- 2μ) = 3p/E x (1 –2/m)
The elongation of a conical bar under its own weight is ......that of prismatic bar of the same length.- a)equal to
- b)half
- c)one-third
- d)two-third
Correct answer is option 'C'. Can you explain this answer?
The elongation of a conical bar under its own weight is ......that of prismatic bar of the same length.
a)
equal to
b)
half
c)
one-third
d)
two-third

|
Shivam Sharma answered |
Conical bar/Prismatic Bar.
= (wl^2/6E) / (wl^2/2E),
=1/3.
A composite shaft consisting of two stepped portions having spring constants k1 and k2 is held between two rigid supports at the ends. Its equivalent spring constant is
- a)

- b)
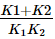
- c)

- d)
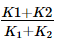
Correct answer is option 'D'. Can you explain this answer?
A composite shaft consisting of two stepped portions having spring constants k1 and k2 is held between two rigid supports at the ends. Its equivalent spring constant is
a)
b)
c)
d)
|
|
Avinash Mehta answered |
To find the equivalent spring constant of the composite shaft, we can use the concept of parallel and series combination of springs.
The composite shaft consists of two stepped portions, each with a different spring constant. Let the spring constants of the two portions be k1 and k2.
Step 1: Find the equivalent spring constant of the first portion (k1).
The first portion of the shaft has a spring constant of k1. Therefore, the equivalent spring constant of this portion is k1.
Step 2: Find the equivalent spring constant of the second portion (k2).
The second portion of the shaft has a spring constant of k2. Therefore, the equivalent spring constant of this portion is k2.
Step 3: Find the equivalent spring constant of the composite shaft.
Since the two portions of the shaft are in series, the equivalent spring constant of the composite shaft can be found using the formula:
1/keq = 1/k1 + 1/k2
where keq is the equivalent spring constant of the composite shaft.
Simplifying the equation, we get:
keq = (k1 * k2) / (k1 + k2)
Therefore, the equivalent spring constant of the composite shaft is (k1 * k2) / (k1 + k2).
Answer: (D) (k1 * k2) / (k1 + k2)
A thin mid steel wire is loaded by adding loads in equal increments till it breaks. The extensions noted with increasing loads will behave as under- a)uniform throughout
- b)first increase and then decrease
- c)increase uniformly first and then increase rapidly
- d)increase rapidly first and then uniformly
Correct answer is option 'C'. Can you explain this answer?
A thin mid steel wire is loaded by adding loads in equal increments till it breaks. The extensions noted with increasing loads will behave as under
a)
uniform throughout
b)
first increase and then decrease
c)
increase uniformly first and then increase rapidly
d)
increase rapidly first and then uniformly
|
|
Neha Joshi answered |
At first, the strain is proportional to strain or elongation is proportional to the load giving a straight-line relationship.
A further increase in the load after yield load will cause marked deformation in the whole volume of the metal. The maximum load which the specimen can withstand without failure is called the load at the ultimate strength.
When a body is subjected to three mutually perpendicular stresses, of equal intensity, the ratio of direct stress to the corresponding volumetric strain is known as- a)Young's modulus
- b)modulus of rigidity
- c)bulk modulus
- d)Poisson's ratio
Correct answer is option 'C'. Can you explain this answer?
When a body is subjected to three mutually perpendicular stresses, of equal intensity, the ratio of direct stress to the corresponding volumetric strain is known as
a)
Young's modulus
b)
modulus of rigidity
c)
bulk modulus
d)
Poisson's ratio

|
Rahul Chatterjee answered |
The bulk modulus of a substance is a measure of how resistant to compressibility that substance is. It is defined as the ratio of the infinitesimal pressure increase to the resulting relative decrease of the volume. Other moduli describe the material's response (strain) to other kinds of stress: the shear modulus describes the response to shear, and Young's modulus describes the response to linear stress. For a fluid, only the bulk modulus is meaningful. For a complex anisotropic solid such as wood or paper, these three moduli do not contain enough information to describe its behaviour, and one must use the full generalized Hooke's law.
Resilience of a material is considered when it is subjected to
- a)fatigue
- b)creep
- c)shock loading
- d)resonant condition
Correct answer is option 'C'. Can you explain this answer?
Resilience of a material is considered when it is subjected to
a)
fatigue
b)
creep
c)
shock loading
d)
resonant condition

|
Rutuja Deshpande answered |
It is the property of materials to absorb energy and to resist shock and impact loads. It is measured by the amount of energy absorbed per unit volume within elastic limit this property is essential for spring materials. The resilience of material should be considered when it is subjected to shock loading.
In a tensile testing experiment on a specimen of 1 cm2 area, the maximum load observed was 5 tonnes and neck area 0.25 cm2. The ultimate tensile strength of specimen is
- a)4 tonnes/cm2
- b)5 tonnes/cm2
- c)16 tonnes/cm2
- d)22 tonnes/cm2
Correct answer is option 'B'. Can you explain this answer?
In a tensile testing experiment on a specimen of 1 cm2 area, the maximum load observed was 5 tonnes and neck area 0.25 cm2. The ultimate tensile strength of specimen is
a)
4 tonnes/cm2
b)
5 tonnes/cm2
c)
16 tonnes/cm2
d)
22 tonnes/cm2
|
|
Sinjini Bose answered |
Ultimate tensile strength is corresponding to the maximum load and cross-sectional area of the specimen at the start of the test.
Ultimate tensile strength =
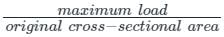
Area = 1 cm2 and maximum load = 5 tonnes
So ultimate tensile strength = 5 tonnes/1 cm2 = 5 tonnes/cm2
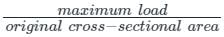
Area = 1 cm2 and maximum load = 5 tonnes
So ultimate tensile strength = 5 tonnes/1 cm2 = 5 tonnes/cm2
Consider the following statements about truestress-strain method/curve:
1. It is more sensitive to changes in both metallurgical and mechanical conditions.
2. It gives a more accurate picture of the ductility.
3. It can be correlated with stress-strain values in other tests like torsion, impact, combined stress tests etc.
4. It can be used for compression tests as well.Which of the above statements are correct?- a)1, 2 and 3
- b)1, 3 and 4
- c)2, 3 and 4
- d)1, 2, 3 and 4
Correct answer is option 'D'. Can you explain this answer?
Consider the following statements about truestress-strain method/curve:
1. It is more sensitive to changes in both metallurgical and mechanical conditions.
2. It gives a more accurate picture of the ductility.
3. It can be correlated with stress-strain values in other tests like torsion, impact, combined stress tests etc.
4. It can be used for compression tests as well.
1. It is more sensitive to changes in both metallurgical and mechanical conditions.
2. It gives a more accurate picture of the ductility.
3. It can be correlated with stress-strain values in other tests like torsion, impact, combined stress tests etc.
4. It can be used for compression tests as well.
Which of the above statements are correct?
a)
1, 2 and 3
b)
1, 3 and 4
c)
2, 3 and 4
d)
1, 2, 3 and 4

|
Nitya Nambiar answered |
Truestress-strain method/curve is a widely used method in materials testing to determine the mechanical behavior of a material under load. It provides valuable information about the material's strength, ductility, and other mechanical properties. Let's analyze each statement to determine their correctness:
Statement 1: It is more sensitive to changes in both metallurgical and mechanical conditions.
- This statement is correct. The truestress-strain method takes into account the instantaneous cross-sectional area of the specimen, which changes during deformation. This makes it more sensitive to changes in the material's mechanical and metallurgical conditions compared to the engineering stress-strain method.
Statement 2: It gives a more accurate picture of the ductility.
- This statement is correct. The truestress-strain curve provides a more accurate representation of the material's ductility because it considers the actual change in cross-sectional area during deformation. It accounts for the necking phenomenon that occurs in many materials under tension, which is crucial for accurately assessing the material's ability to deform before failure.
Statement 3: It can be correlated with stress-strain values in other tests like torsion, impact, combined stress tests, etc.
- This statement is correct. The truestress-strain values obtained from tensile testing can be correlated with stress-strain values obtained from other testing methods like torsion, impact, and combined stress tests. This allows for a better understanding of the material's behavior under different loading conditions and helps in predicting its performance in various applications.
Statement 4: It can be used for compression tests as well.
- This statement is correct. While the truestress-strain method is commonly used in tensile testing, it can also be applied to compression testing. The concept of truestress and truestrain can be extended to compression tests by considering the instantaneous cross-sectional area and volume changes during deformation.
In conclusion, all the given statements about the truestress-strain method/curve are correct. It is a sensitive method that provides a more accurate picture of ductility, can be correlated with other test results, and can be used for both tension and compression testing.
Statement 1: It is more sensitive to changes in both metallurgical and mechanical conditions.
- This statement is correct. The truestress-strain method takes into account the instantaneous cross-sectional area of the specimen, which changes during deformation. This makes it more sensitive to changes in the material's mechanical and metallurgical conditions compared to the engineering stress-strain method.
Statement 2: It gives a more accurate picture of the ductility.
- This statement is correct. The truestress-strain curve provides a more accurate representation of the material's ductility because it considers the actual change in cross-sectional area during deformation. It accounts for the necking phenomenon that occurs in many materials under tension, which is crucial for accurately assessing the material's ability to deform before failure.
Statement 3: It can be correlated with stress-strain values in other tests like torsion, impact, combined stress tests, etc.
- This statement is correct. The truestress-strain values obtained from tensile testing can be correlated with stress-strain values obtained from other testing methods like torsion, impact, and combined stress tests. This allows for a better understanding of the material's behavior under different loading conditions and helps in predicting its performance in various applications.
Statement 4: It can be used for compression tests as well.
- This statement is correct. While the truestress-strain method is commonly used in tensile testing, it can also be applied to compression testing. The concept of truestress and truestrain can be extended to compression tests by considering the instantaneous cross-sectional area and volume changes during deformation.
In conclusion, all the given statements about the truestress-strain method/curve are correct. It is a sensitive method that provides a more accurate picture of ductility, can be correlated with other test results, and can be used for both tension and compression testing.
The ability of a material to resist plastic deformation known as _____________- a)Tensile strength
- b)Modulus of elasticity
- c)Yield strength
- d)Impact strength
Correct answer is option 'C'. Can you explain this answer?
The ability of a material to resist plastic deformation known as _____________
a)
Tensile strength
b)
Modulus of elasticity
c)
Yield strength
d)
Impact strength
|
|
Avinash Sharma answered |
The point of stretching where it increases suddenly is known as yield strength, i.e. the region where the stretch is elastic. Tensile strength is the force needed to fracture the material. Impact strength is the capacity of a material to resist shock energy before a fracture.
A wire is stretched by a force. If its length increases by 1%, what is the strain?- a)0.1
- b)0.01
- c)1
- d)10
Correct answer is option 'B'. Can you explain this answer?
A wire is stretched by a force. If its length increases by 1%, what is the strain?
a)
0.1
b)
0.01
c)
1
d)
10

|
Crack Gate answered |
If a wire is stretched by a force and its length increases by 1%, the strain can be calculated as follows:
- Strain is defined as the change in length divided by the original length.
- In this case, the change in length is 1% of the original length.
- Therefore, strain = (Change in Length) / (Original Length).
- As a decimal, 1% is equal to 0.01.
Thus, the strain is 0.01. The correct answer is B.
What is the unit of Young’s modulus in the SI system?- a)N/m
- b)N/m²
- c)Pa
- d)N
Correct answer is option 'C'. Can you explain this answer?
What is the unit of Young’s modulus in the SI system?
a)
N/m
b)
N/m²
c)
Pa
d)
N

|
Pk Academy answered |
Young's modulus is a measure of the stiffness of a material. In the SI system, the unit of Young's modulus is the Pascal, abbreviated as Pa.
A bolt is made to pass through a tube and both of them are tightly fitted with the holp of washer sand nuts. If the nut is tightened, then- a)bolt and tube are under tension
- b)bolt and tube under compression
- c)bolt is under compression and tube is under tension
- d)bolt is under tension and tube is under compression
Correct answer is option 'D'. Can you explain this answer?
A bolt is made to pass through a tube and both of them are tightly fitted with the holp of washer sand nuts. If the nut is tightened, then
a)
bolt and tube are under tension
b)
bolt and tube under compression
c)
bolt is under compression and tube is under tension
d)
bolt is under tension and tube is under compression

|
Gandharv Dhayatkar answered |
Answer option is pretty self explanatory.
As we tighten the nut, the nut pulls the bolt(hence tensile force) and pushes on the tube (compressive force).
As we tighten the nut, the nut pulls the bolt(hence tensile force) and pushes on the tube (compressive force).
Hooke's law holds good upto
- a)yield point
- b)limit of proportionality
- c)breaking point
- d)inelastic limit
- e)plastic limit
Correct answer is option 'B'. Can you explain this answer?
Hooke's law holds good upto
a)
yield point
b)
limit of proportionality
c)
breaking point
d)
inelastic limit
e)
plastic limit
|
|
Dhruv Dasgupta answered |
Hookes law is a fundamental law of nature that describes the relationship between the deformation and the applied force of an elastic body. It states that, within the elastic limit, the deformation or strain of an elastic material is proportional to the applied force or stress. However, Hookes law does not hold good beyond a certain limit. The correct option for this limit is B, the limit of proportionality.
Explanation:
Limit of proportionality is defined as the maximum stress or force that can be applied to a material such that the stress-strain relationship remains linear. Beyond this limit, the stress-strain relationship becomes nonlinear, and the material begins to show plastic deformation. At this point, Hookes law no longer holds true.
To understand this concept better, let us consider the stress-strain curve of a typical metallic material. The curve can be divided into several regions based on the response of the material to applied stress.
1. Elastic Region: In this region, the material behaves elastically, and the deformation is proportional to the applied force. Hookes law holds good in this region.
2. Yield Point: Beyond the elastic region, the material enters the plastic region, and it begins to deform permanently. The yield point is defined as the point where the material begins to show plastic deformation. At this point, Hookes law no longer holds good.
3. Plastic Region: In this region, the material undergoes permanent deformation, and the stress-strain relationship is nonlinear.
4. Ultimate Tensile Strength: The maximum stress that a material can withstand before it breaks is called the ultimate tensile strength.
In conclusion, Hookes law holds good up to the limit of proportionality, which is the point beyond which the stress-strain relationship becomes nonlinear. Beyond this point, the material begins to undergo plastic deformation, and Hookes law is no longer valid.
Explanation:
Limit of proportionality is defined as the maximum stress or force that can be applied to a material such that the stress-strain relationship remains linear. Beyond this limit, the stress-strain relationship becomes nonlinear, and the material begins to show plastic deformation. At this point, Hookes law no longer holds true.
To understand this concept better, let us consider the stress-strain curve of a typical metallic material. The curve can be divided into several regions based on the response of the material to applied stress.
1. Elastic Region: In this region, the material behaves elastically, and the deformation is proportional to the applied force. Hookes law holds good in this region.
2. Yield Point: Beyond the elastic region, the material enters the plastic region, and it begins to deform permanently. The yield point is defined as the point where the material begins to show plastic deformation. At this point, Hookes law no longer holds good.
3. Plastic Region: In this region, the material undergoes permanent deformation, and the stress-strain relationship is nonlinear.
4. Ultimate Tensile Strength: The maximum stress that a material can withstand before it breaks is called the ultimate tensile strength.
In conclusion, Hookes law holds good up to the limit of proportionality, which is the point beyond which the stress-strain relationship becomes nonlinear. Beyond this point, the material begins to undergo plastic deformation, and Hookes law is no longer valid.
The neutral axis of the cross-section a beam is that axis at which the bending stress is- a)Zero
- b)minimum
- c)maximum
- d)infinity
Correct answer is option 'A'. Can you explain this answer?
The neutral axis of the cross-section a beam is that axis at which the bending stress is
a)
Zero
b)
minimum
c)
maximum
d)
infinity

|
Anirban Khanna answered |
Neutral axis is the line interaction with neutral layer with transverse axis. In above neutral axis the layers are compressed and below the layers are tensed. There is no load acting on neutral axis. So bending moment on the neutral axis is zero.
Hook's law holds good up to- a)yield point
- b)elastic limit
- c)plastic limit
- d)breaking point
Correct answer is option 'B'. Can you explain this answer?
Hook's law holds good up to
a)
yield point
b)
elastic limit
c)
plastic limit
d)
breaking point

|
Kaavya Sengupta answered |
Hooke's law is only really valid up to the proportionality limit, and this is simply because Hooke's law is a proportionality law, i.e. Force (or stress) is proportional to extension (or strain).
Damping capacity of a material is its ability to- a)absorb shock
- b)withstand compression
- c)absorb impact loads
- d)withstand creep failures
Correct answer is option 'B'. Can you explain this answer?
Damping capacity of a material is its ability to
a)
absorb shock
b)
withstand compression
c)
absorb impact loads
d)
withstand creep failures
|
|
Anshu Patel answered |
Damping Capacity
Damping capacity refers to the ability of a material to dissipate energy when subjected to mechanical stress or vibration. This energy dissipation is often referred to as damping.
Compression Strength
Compression strength is the measure of a material's ability to withstand compressive loads or forces without breaking or deforming.
Relation between Damping Capacity and Compression Strength
The damping capacity of a material is related to its compression strength. The higher the compression strength of a material, the better its damping capacity.
When a material is subjected to mechanical stress or vibration, it undergoes deformation. The energy required for this deformation is stored in the material. If the material has a high damping capacity, it can dissipate this energy quickly, preventing it from building up and causing damage.
Materials with high compression strength are better able to withstand the stresses and forces that cause vibration and mechanical stress. As a result, they are better equipped to handle the energy dissipation required for damping.
Conclusion
In conclusion, damping capacity is related to a material's ability to withstand mechanical stress and vibration. Compression strength is an important factor in determining a material's damping capacity. Materials that have high compression strength are better equipped to handle the energy dissipation required for damping.
Damping capacity refers to the ability of a material to dissipate energy when subjected to mechanical stress or vibration. This energy dissipation is often referred to as damping.
Compression Strength
Compression strength is the measure of a material's ability to withstand compressive loads or forces without breaking or deforming.
Relation between Damping Capacity and Compression Strength
The damping capacity of a material is related to its compression strength. The higher the compression strength of a material, the better its damping capacity.
When a material is subjected to mechanical stress or vibration, it undergoes deformation. The energy required for this deformation is stored in the material. If the material has a high damping capacity, it can dissipate this energy quickly, preventing it from building up and causing damage.
Materials with high compression strength are better able to withstand the stresses and forces that cause vibration and mechanical stress. As a result, they are better equipped to handle the energy dissipation required for damping.
Conclusion
In conclusion, damping capacity is related to a material's ability to withstand mechanical stress and vibration. Compression strength is an important factor in determining a material's damping capacity. Materials that have high compression strength are better equipped to handle the energy dissipation required for damping.
Bulk modulus is defined as:- a)Pressure / volume strain
- b)Stress / strain in length
- c)Volume strain / pressure
- d)Lateral strain / longitudinal strain
Correct answer is option 'A'. Can you explain this answer?
Bulk modulus is defined as:
a)
Pressure / volume strain
b)
Stress / strain in length
c)
Volume strain / pressure
d)
Lateral strain / longitudinal strain

|
Constructing Careers answered |
Bulk modulus is defined as:
- Pressure divided by volume strain. So (a) is the right option.
A bolt is made to pass through a tube and both of them are tightly fitted with the holp of washer sand nuts. If the nut is tightened, then- a)bolt and tube are under tension
- b)bolt and tube under compression
- c)bolt is under compression and tube is under tension
- d)bolt is under tension and tube is under compression
Correct answer is 'D'. Can you explain this answer?
A bolt is made to pass through a tube and both of them are tightly fitted with the holp of washer sand nuts. If the nut is tightened, then
a)
bolt and tube are under tension
b)
bolt and tube under compression
c)
bolt is under compression and tube is under tension
d)
bolt is under tension and tube is under compression

|
Bijoy Kapoor answered |
As the nut is exerting compressive force to the washer ,then ultimately it will compress the tube and if something is compressed it will exert stress(resisting force) here resisting force against compression is tensile stress. so tensile stress will act against bolt so it will feel tension.
A prismatic bar of circular cross-section is loaded by tensile forces P= 90 kN. The bar has length L = 3 m and diameter d = 30 mm. If is made of aluminium with modulus of elasticity E = 70 GPa and Poisson’s ratio v = 1/3. What is the increase in volume ΔV of the bar?- a)800 mm3
- b)1000 mm3
- c)1285 mm3
- d)1412 mm3
Correct answer is option 'C'. Can you explain this answer?
A prismatic bar of circular cross-section is loaded by tensile forces P= 90 kN. The bar has length L = 3 m and diameter d = 30 mm. If is made of aluminium with modulus of elasticity E = 70 GPa and Poisson’s ratio v = 1/3. What is the increase in volume ΔV of the bar?
a)
800 mm3
b)
1000 mm3
c)
1285 mm3
d)
1412 mm3
|
|
Rajat Basu answered |
's ratio ν = 0.33. Determine:
a) The normal stress on a plane perpendicular to the axis of the bar.
b) The normal strain on a plane perpendicular to the axis of the bar.
c) The change in length of the bar.
d) The lateral strain on a plane parallel to the axis of the bar.
Solution:
a) The normal stress on a plane perpendicular to the axis of the bar is given by:
σ = P/A
where P is the applied load and A is the cross-sectional area of the bar. Since the bar has a circular cross-section, the area is given by:
A = πd^2/4
Substituting the given values, we have:
A = π(0.03 m)^2/4 = 7.07 × 10^-4 m^2
σ = 90 kN/7.07 × 10^-4 m^2 = 127.3 MPa
Therefore, the normal stress on a plane perpendicular to the axis of the bar is 127.3 MPa.
b) The normal strain on a plane perpendicular to the axis of the bar is given by:
ε = σ/E
Substituting the values obtained in part a) and the given values, we have:
ε = 127.3 MPa/70 GPa = 0.00182
Therefore, the normal strain on a plane perpendicular to the axis of the bar is 0.00182.
c) The change in length of the bar is given by:
ΔL = εL
Substituting the value obtained in part b) and the given values, we have:
ΔL = 0.00182 × 3 m = 0.00546 m
Therefore, the change in length of the bar is 0.00546 m.
d) The lateral strain on a plane parallel to the axis of the bar is given by:
νε = νσ/E
Substituting the values obtained in part a) and b) and the given values, we have:
νε = 0.33 × 127.3 MPa/70 GPa = 0.000603
Therefore, the lateral strain on a plane parallel to the axis of the bar is 0.000603.
a) The normal stress on a plane perpendicular to the axis of the bar.
b) The normal strain on a plane perpendicular to the axis of the bar.
c) The change in length of the bar.
d) The lateral strain on a plane parallel to the axis of the bar.
Solution:
a) The normal stress on a plane perpendicular to the axis of the bar is given by:
σ = P/A
where P is the applied load and A is the cross-sectional area of the bar. Since the bar has a circular cross-section, the area is given by:
A = πd^2/4
Substituting the given values, we have:
A = π(0.03 m)^2/4 = 7.07 × 10^-4 m^2
σ = 90 kN/7.07 × 10^-4 m^2 = 127.3 MPa
Therefore, the normal stress on a plane perpendicular to the axis of the bar is 127.3 MPa.
b) The normal strain on a plane perpendicular to the axis of the bar is given by:
ε = σ/E
Substituting the values obtained in part a) and the given values, we have:
ε = 127.3 MPa/70 GPa = 0.00182
Therefore, the normal strain on a plane perpendicular to the axis of the bar is 0.00182.
c) The change in length of the bar is given by:
ΔL = εL
Substituting the value obtained in part b) and the given values, we have:
ΔL = 0.00182 × 3 m = 0.00546 m
Therefore, the change in length of the bar is 0.00546 m.
d) The lateral strain on a plane parallel to the axis of the bar is given by:
νε = νσ/E
Substituting the values obtained in part a) and b) and the given values, we have:
νε = 0.33 × 127.3 MPa/70 GPa = 0.000603
Therefore, the lateral strain on a plane parallel to the axis of the bar is 0.000603.
A closely-coiled helical spring is cut into two halves. The stiffness of the resulting spring will be- a)same
- b)double
- c)half
- d)one-fourth
Correct answer is option 'D'. Can you explain this answer?
A closely-coiled helical spring is cut into two halves. The stiffness of the resulting spring will be
a)
same
b)
double
c)
half
d)
one-fourth
|
|
Stuti Mishra answered |
Stiffness of a Spring When Cut into Two Halves
When a closely-coiled helical spring is cut into two halves, the stiffness of the resulting spring will change. Here's how:
1. Definition of Stiffness: Stiffness is the ability of a spring to resist deformation when subjected to an external force. It is defined as the force required to extend or compress the spring by a unit length.
2. Stiffness of a Spring: The stiffness of a spring depends on the material of the spring, the cross-sectional area of the wire, the length of the spring, and the number of coils. The formula for stiffness is given by:
K = (Gd^4)/(8nD^3)
where K is the stiffness, G is the modulus of rigidity of the material, d is the diameter of the wire, n is the number of coils, and D is the diameter of the spring.
3. Cutting a Spring: When a spring is cut into two halves, the number of coils is reduced by half. This means that the stiffness of the resulting spring will be different from that of the original spring.
4. Calculation of Stiffness: To calculate the stiffness of the resulting spring, we can use the formula for stiffness and substitute the new values. Since the number of coils is reduced by half, n becomes n/2. Therefore, the new stiffness is given by:
K' = (Gd^4)/(8(n/2)D^3)
= 2(Gd^4)/(8nD^3)
= 2K
where K' is the new stiffness and K is the original stiffness.
5. Conclusion: From the above calculation, we can see that the stiffness of the resulting spring is double that of the original spring. Therefore, the correct answer is option 'B' - double.
When a closely-coiled helical spring is cut into two halves, the stiffness of the resulting spring will change. Here's how:
1. Definition of Stiffness: Stiffness is the ability of a spring to resist deformation when subjected to an external force. It is defined as the force required to extend or compress the spring by a unit length.
2. Stiffness of a Spring: The stiffness of a spring depends on the material of the spring, the cross-sectional area of the wire, the length of the spring, and the number of coils. The formula for stiffness is given by:
K = (Gd^4)/(8nD^3)
where K is the stiffness, G is the modulus of rigidity of the material, d is the diameter of the wire, n is the number of coils, and D is the diameter of the spring.
3. Cutting a Spring: When a spring is cut into two halves, the number of coils is reduced by half. This means that the stiffness of the resulting spring will be different from that of the original spring.
4. Calculation of Stiffness: To calculate the stiffness of the resulting spring, we can use the formula for stiffness and substitute the new values. Since the number of coils is reduced by half, n becomes n/2. Therefore, the new stiffness is given by:
K' = (Gd^4)/(8(n/2)D^3)
= 2(Gd^4)/(8nD^3)
= 2K
where K' is the new stiffness and K is the original stiffness.
5. Conclusion: From the above calculation, we can see that the stiffness of the resulting spring is double that of the original spring. Therefore, the correct answer is option 'B' - double.
The longitudinal stress induced in a thin walled cylindrical vessel is- a)pD/2t
- b)pD/4t
- c)pD/t
- d)pD/3t
- e)pD/6t
Correct answer is option 'B'. Can you explain this answer?
The longitudinal stress induced in a thin walled cylindrical vessel is
a)
pD/2t
b)
pD/4t
c)
pD/t
d)
pD/3t
e)
pD/6t

|
Debolina Chavan answered |
Longitudinal stress in a thin-walled cylindrical vessel:
The longitudinal stress induced in a thin-walled cylindrical vessel can be determined using the formula:
σ = pD/4t
where:
- σ is the longitudinal stress
- p is the internal pressure
- D is the diameter of the cylindrical vessel
- t is the thickness of the cylindrical vessel wall
Derivation:
To understand the derivation of the formula, let's consider a thin-walled cylindrical vessel subjected to internal pressure. The vessel can be imagined as a hollow cylinder with an inner radius (r) and outer radius (R).
1. Assumptions:
- The cylindrical vessel is thin-walled, meaning that the thickness of the wall is much smaller compared to the radius of the vessel.
- The vessel is homogeneous and isotropic, meaning that its material properties are uniform in all directions.
2. Equilibrium:
Under the action of internal pressure (p), the cylinder experiences a net force in the axial direction. To maintain equilibrium, an equal and opposite force must be applied to counteract this pressure.
3. Stress:
The force per unit area acting on the cylindrical vessel is defined as stress (σ). In this case, the stress is acting longitudinally along the axial direction.
4. Equations:
- The axial force acting on the cylindrical vessel can be calculated using the equation: F = pA, where A is the cross-sectional area of the vessel.
- The cross-sectional area of the vessel is given by: A = π(R^2 - r^2).
- The axial stress is defined as: σ = F/A.
5. Solution:
By substituting the equations above, we get:
σ = pA / A
σ = pπ(R^2 - r^2) / π(R^2 - r^2)
σ = p(R^2 - r^2) / (R^2 - r^2)
Since the vessel is thin-walled, r ≈ R. Therefore, we can simplify the equation to:
σ = p(R^2 - R^2) / (R^2 - R^2)
σ ≈ pR^2 / R^2
σ ≈ p
This means that the longitudinal stress (σ) induced in a thin-walled cylindrical vessel is approximately equal to the internal pressure (p).
6. Final formula:
However, if we consider the effect of wall thickness (t), the formula for longitudinal stress becomes:
σ = pD/4t
Conclusion:
The correct answer is option 'B': pD/4t. This formula takes into account the effect of both internal pressure (p) and wall thickness (t) on the longitudinal stress induced in a thin-walled cylindrical vessel.
The longitudinal stress induced in a thin-walled cylindrical vessel can be determined using the formula:
σ = pD/4t
where:
- σ is the longitudinal stress
- p is the internal pressure
- D is the diameter of the cylindrical vessel
- t is the thickness of the cylindrical vessel wall
Derivation:
To understand the derivation of the formula, let's consider a thin-walled cylindrical vessel subjected to internal pressure. The vessel can be imagined as a hollow cylinder with an inner radius (r) and outer radius (R).
1. Assumptions:
- The cylindrical vessel is thin-walled, meaning that the thickness of the wall is much smaller compared to the radius of the vessel.
- The vessel is homogeneous and isotropic, meaning that its material properties are uniform in all directions.
2. Equilibrium:
Under the action of internal pressure (p), the cylinder experiences a net force in the axial direction. To maintain equilibrium, an equal and opposite force must be applied to counteract this pressure.
3. Stress:
The force per unit area acting on the cylindrical vessel is defined as stress (σ). In this case, the stress is acting longitudinally along the axial direction.
4. Equations:
- The axial force acting on the cylindrical vessel can be calculated using the equation: F = pA, where A is the cross-sectional area of the vessel.
- The cross-sectional area of the vessel is given by: A = π(R^2 - r^2).
- The axial stress is defined as: σ = F/A.
5. Solution:
By substituting the equations above, we get:
σ = pA / A
σ = pπ(R^2 - r^2) / π(R^2 - r^2)
σ = p(R^2 - r^2) / (R^2 - r^2)
Since the vessel is thin-walled, r ≈ R. Therefore, we can simplify the equation to:
σ = p(R^2 - R^2) / (R^2 - R^2)
σ ≈ pR^2 / R^2
σ ≈ p
This means that the longitudinal stress (σ) induced in a thin-walled cylindrical vessel is approximately equal to the internal pressure (p).
6. Final formula:
However, if we consider the effect of wall thickness (t), the formula for longitudinal stress becomes:
σ = pD/4t
Conclusion:
The correct answer is option 'B': pD/4t. This formula takes into account the effect of both internal pressure (p) and wall thickness (t) on the longitudinal stress induced in a thin-walled cylindrical vessel.
Which of the following statements is true about strain?- a)It has units of pressure
- b)It is equal to the applied force
- c)It is measured in N/m²
- d)It is a dimensionless quantity
Correct answer is option 'D'. Can you explain this answer?
Which of the following statements is true about strain?
a)
It has units of pressure
b)
It is equal to the applied force
c)
It is measured in N/m²
d)
It is a dimensionless quantity

|
Gate Funda answered |
Strain is a measure of deformation representing the displacement between particles in a material body. It is expressed as a ratio of change in length to the original length, making it a dimensionless quantity. Here are key points regarding strain:
- Strain has no units, as it is a ratio.
- It is not measured in N/m²; that is a unit for stress.
- Strain does not equal the applied force; it represents how much a material deforms.
Thus, the correct statement is that strain is a dimensionless quantity.
An overhanging beam is- a)same as cantilever
- b)not same as cantilever
- c)one which extends beyond its support at either end
- d)one which extends beyond its support at both ends
- e)none of the above
Correct answer is option 'C'. Can you explain this answer?
An overhanging beam is
a)
same as cantilever
b)
not same as cantilever
c)
one which extends beyond its support at either end
d)
one which extends beyond its support at both ends
e)
none of the above
|
|
Ameya Kaur answered |
Definition of an Overhanging Beam:
An overhanging beam is a type of structural element that extends beyond its support at one or both ends. It is similar to a cantilever in that it has a protruding section, but it is not exactly the same.
Explanation:
To better understand the concept of an overhanging beam, let's break down the question and its options:
A) Same as Cantilever:
This option suggests that an overhanging beam is identical to a cantilever. While there are similarities between the two, they are not exactly the same. Both involve a beam that extends beyond its support, but a cantilever refers specifically to a beam that extends from a fixed point and is supported only at one end.
B) Not the same as Cantilever:
This option correctly states that an overhanging beam is not the same as a cantilever. As mentioned above, a cantilever is a specific type of overhanging beam, but not all overhanging beams are cantilevers.
C) Extends beyond its support at either end:
This option accurately describes an overhanging beam. It means that the beam extends beyond its support at one or both ends. In other words, the beam hangs over the edge or extends past the point where it is supported, creating an overhanging section.
D) Extends beyond its support at both ends:
This option incorrectly suggests that an overhanging beam extends beyond its support at both ends. However, this is not the case. An overhanging beam can extend beyond its support at one end or both ends, but it is not necessary for it to extend beyond both ends.
Therefore, the correct answer is Option C: One which extends beyond its support at either end.
An overhanging beam is a type of structural element that extends beyond its support at one or both ends. It is similar to a cantilever in that it has a protruding section, but it is not exactly the same.
Explanation:
To better understand the concept of an overhanging beam, let's break down the question and its options:
A) Same as Cantilever:
This option suggests that an overhanging beam is identical to a cantilever. While there are similarities between the two, they are not exactly the same. Both involve a beam that extends beyond its support, but a cantilever refers specifically to a beam that extends from a fixed point and is supported only at one end.
B) Not the same as Cantilever:
This option correctly states that an overhanging beam is not the same as a cantilever. As mentioned above, a cantilever is a specific type of overhanging beam, but not all overhanging beams are cantilevers.
C) Extends beyond its support at either end:
This option accurately describes an overhanging beam. It means that the beam extends beyond its support at one or both ends. In other words, the beam hangs over the edge or extends past the point where it is supported, creating an overhanging section.
D) Extends beyond its support at both ends:
This option incorrectly suggests that an overhanging beam extends beyond its support at both ends. However, this is not the case. An overhanging beam can extend beyond its support at one end or both ends, but it is not necessary for it to extend beyond both ends.
Therefore, the correct answer is Option C: One which extends beyond its support at either end.
The following statements are associated with the stress-strain diagram for steel. - For small values of the strain, the relationship is linear (straight line), and the stress is proportional to the strain. This behavior is valid until the stress reaches the proportional limit.
- If the stress exceeds the proportional limit, the strain begins to increase more rapidly, and the slope of the curve decreases.
- a)1 and 2 are correct
- b)1 and 2 are wrong
- c)1 correct and 2 wrong
- d)1 wrong and 2 correct
Correct answer is option 'A'. Can you explain this answer?
The following statements are associated with the stress-strain diagram for steel.
- For small values of the strain, the relationship is linear (straight line), and the stress is proportional to the strain. This behavior is valid until the stress reaches the proportional limit.
- If the stress exceeds the proportional limit, the strain begins to increase more rapidly, and the slope of the curve decreases.
a)
1 and 2 are correct
b)
1 and 2 are wrong
c)
1 correct and 2 wrong
d)
1 wrong and 2 correct

|
Pk Academy answered |
The stress-strain diagram for steel is a graphical representation of the relationship between stress and strain during the deformation of steel. The diagram typically shows stress on the y-axis and strain on the x-axis.
Statement 1 is correct because, for small values of strain, the relationship between stress and strain is linear, and stress is proportional to strain. This behavior is known as Hooke’s Law, and it is valid until the stress reaches the proportional limit. The proportional limit is the point beyond which the relationship between stress and strain is no longer linear.
Statement 2 is also correct because, if the stress exceeds the proportional limit, the strain begins to increase more rapidly, and the slope of the curve decreases. This behavior is due to the onset of plastic deformation, which causes the steel to permanently deform even after the stress is removed. The stress at which plastic deformation begins is known as the yield strength, and it is typically higher than the proportional limit.
Therefore, both statements 1 and 2 are correct.
In the elastic limit, which law is followed by solids under tensile stress?- a)Pascal’s law
- b)Newton’s law
- c)Hooke’s law
- d)Bernoulli’s principle
Correct answer is option 'C'. Can you explain this answer?
In the elastic limit, which law is followed by solids under tensile stress?
a)
Pascal’s law
b)
Newton’s law
c)
Hooke’s law
d)
Bernoulli’s principle

|
Telecom Tuners answered |
Hooke’s law describes the behaviour of solids under tensile stress within the elastic limit. It states that the strain in a material is proportional to the applied stress, provided the material's elastic limit is not exceeded. This can be summarised as:
- Stress is the force applied per unit area.
- Strain is the deformation experienced by the material.
- In simple terms, as you stretch a solid, it stretches proportionally up to a certain point.
Which of the following best defines stress?- a)Extension per unit length
- b)Strain per unit force
- c)Force per unit area
- d)Force multiplied by area
Correct answer is option 'C'. Can you explain this answer?
Which of the following best defines stress?
a)
Extension per unit length
b)
Strain per unit force
c)
Force per unit area
d)
Force multiplied by area

|
Pk Academy answered |
Stress is best defined as the force applied per unit area. It measures how much force is distributed over a specific area and is crucial in understanding material behaviour under load. The correct definition can be summarised as follows:
- Force per unit area indicates how pressure is applied to an object.
- This concept is essential in fields such as engineering and physics.
- Understanding stress helps predict how materials will respond to external forces.
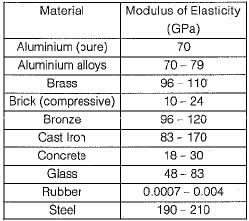
Match List-1 (Materia!) with List-ll (Poisson’s Ratio)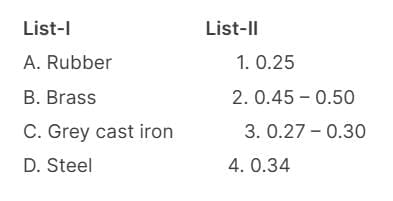
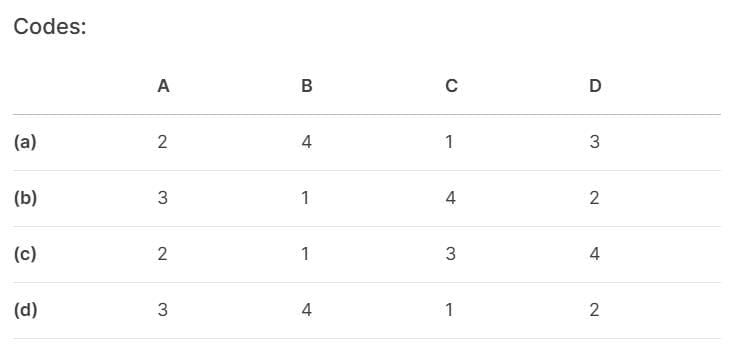
- a)a
- b)b
- c)c
- d)d
Correct answer is option 'A'. Can you explain this answer?
Match List-1 (Materia!) with List-ll (Poisson’s Ratio)


a)
a
b)
b
c)
c
d)
d

|
Gate Funda answered |
To match List-I (Materials) with List-II (Poisson's Ratio), it's essential to know typical values for each material:
- Rubber: Poisson's ratio is typically around 0.5.
- Brass: Ranges from 0.34 to 0.36.
- Grey cast iron: Around 0.25 - 0.30.
- Steel: Approximately 0.27 - 0.30.
This corresponds to the code (a) 2 4 1 3
Thus option A is correct.
Moment of a beam is defined as its section modulus multiplied by- a)moment of inertia
- b)stress
- c)strain
- d)coefficient of elasticity
- e)half the depth
Correct answer is option 'B'. Can you explain this answer?
Moment of a beam is defined as its section modulus multiplied by
a)
moment of inertia
b)
stress
c)
strain
d)
coefficient of elasticity
e)
half the depth
|
|
Gaurav Kapoor answered |
Explanation:
The moment of a beam refers to the ability of the beam to resist bending or twisting moments. It is a measure of the beam's resistance to bending under an applied load. The moment of a beam is determined by its section modulus, which is a property of the beam's cross-sectional shape.
Moment of Inertia:
The moment of inertia is a measure of an object's resistance to changes in its rotational motion. It depends on the distribution of mass around the axis of rotation. The moment of inertia of a beam is related to its section modulus through the equation: moment of inertia = section modulus * area. Therefore, the moment of inertia is not directly related to the moment of a beam.
Stress:
Stress is a measure of the internal forces within a material caused by an external load. It is defined as the force per unit area. Stress is not directly related to the moment of a beam.
Strain:
Strain is a measure of the deformation of a material caused by an external load. It is defined as the change in length per unit length. Strain is not directly related to the moment of a beam.
Coefficient of Elasticity:
The coefficient of elasticity, also known as Young's modulus, is a measure of a material's stiffness. It relates the stress in a material to the strain it experiences. The coefficient of elasticity is not directly related to the moment of a beam.
Half the Depth:
The depth of a beam is one of the factors that determine its section modulus. The section modulus is directly proportional to the depth of the beam. However, half the depth of a beam is not directly related to the moment of the beam.
Therefore, the correct answer is option B, moment of inertia. The moment of a beam is defined as its section modulus multiplied by the moment of inertia of its cross-sectional shape. The section modulus takes into account both the shape and size of the beam, while the moment of inertia accounts for the distribution of mass around the axis of rotation.
Chapter doubts & questions for Strength of Materials (SOM) - Mechanical Engineering SSC JE (Technical) 2025 is part of Mechanical Engineering exam preparation. The chapters have been prepared according to the Mechanical Engineering exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Mechanical Engineering 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Strength of Materials (SOM) - Mechanical Engineering SSC JE (Technical) in English & Hindi are available as part of Mechanical Engineering exam.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
Mechanical Engineering SSC JE (Technical)
6 videos|104 docs|59 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup