NEET Exam > NEET Questions > Orbits of a particle moving in a circle are s...
Start Learning for Free
Orbits of a particle moving in a circle are such that the perimeter of the orbit equals an integer number of de-broglie wavelengths of the particle.For a charged particle moving in a plane perpendicular to a magnetic field,the radius of the nth orbital will be therefore proportional to. 1)n^2. 2)n. 3)n^3/2. 4)n^1/4.?
Verified Answer
Orbits of a particle moving in a circle are such that the perimeter of...
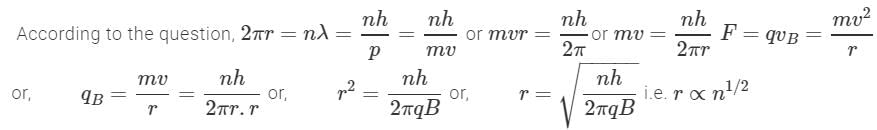
 This question is part of UPSC exam. View all NEET courses
This question is part of UPSC exam. View all NEET courses
Most Upvoted Answer
Orbits of a particle moving in a circle are such that the perimeter of...
Radius of the nth orbital for a charged particle moving in a plane perpendicular to a magnetic field
To understand the relationship between the radius of the nth orbital and the given options, let's consider the scenario of a charged particle moving in a plane perpendicular to a magnetic field.
Lorentz Force
When a charged particle moves through a magnetic field, it experiences a force known as the Lorentz force. The Lorentz force acting on a charged particle moving with velocity v in a magnetic field B is given by the equation F = qvBsinθ, where q is the charge of the particle and θ is the angle between the velocity vector and the magnetic field vector.
Circular Motion
When the magnetic field is perpendicular to the plane of motion, the Lorentz force acts as a centripetal force, causing the charged particle to move in a circle. This circular motion can be described using the equation F_c = mv^2/r, where m is the mass of the particle, v is its velocity, and r is the radius of the orbit.
De Broglie Wavelength
The de Broglie wavelength of a particle is given by the equation λ = h/p, where λ is the wavelength, h is the Planck's constant, and p is the momentum of the particle. In the case of circular motion, the momentum can be related to the velocity and mass of the particle through the equation p = mv.
Perimeter of the Orbit
The perimeter of the orbit is equal to the circumference of the circle, which is given by the equation C = 2πr, where r is the radius of the orbit.
Now, according to the given condition, the perimeter of the orbit should equal an integer number of de Broglie wavelengths of the particle.
2πr = nλ, where n is an integer representing the number of de Broglie wavelengths.
Proportional Relationship
To determine the relationship between the radius of the nth orbital and the given options, we can rearrange the equation 2πr = nλ and substitute the de Broglie wavelength equation λ = h/p.
2πr = n(h/p)
Since p = mv, we can rewrite the equation as:
2πr = nh/mv
Comparing the equation with the equation for circular motion F_c = mv^2/r, we can see that nh/m represents the centripetal force.
Therefore, the radius of the nth orbital is proportional to the square root of n, which corresponds to option 3) n^3/2.
Hence, the correct answer is option 3) n^3/2.
To understand the relationship between the radius of the nth orbital and the given options, let's consider the scenario of a charged particle moving in a plane perpendicular to a magnetic field.
Lorentz Force
When a charged particle moves through a magnetic field, it experiences a force known as the Lorentz force. The Lorentz force acting on a charged particle moving with velocity v in a magnetic field B is given by the equation F = qvBsinθ, where q is the charge of the particle and θ is the angle between the velocity vector and the magnetic field vector.
Circular Motion
When the magnetic field is perpendicular to the plane of motion, the Lorentz force acts as a centripetal force, causing the charged particle to move in a circle. This circular motion can be described using the equation F_c = mv^2/r, where m is the mass of the particle, v is its velocity, and r is the radius of the orbit.
De Broglie Wavelength
The de Broglie wavelength of a particle is given by the equation λ = h/p, where λ is the wavelength, h is the Planck's constant, and p is the momentum of the particle. In the case of circular motion, the momentum can be related to the velocity and mass of the particle through the equation p = mv.
Perimeter of the Orbit
The perimeter of the orbit is equal to the circumference of the circle, which is given by the equation C = 2πr, where r is the radius of the orbit.
Now, according to the given condition, the perimeter of the orbit should equal an integer number of de Broglie wavelengths of the particle.
2πr = nλ, where n is an integer representing the number of de Broglie wavelengths.
Proportional Relationship
To determine the relationship between the radius of the nth orbital and the given options, we can rearrange the equation 2πr = nλ and substitute the de Broglie wavelength equation λ = h/p.
2πr = n(h/p)
Since p = mv, we can rewrite the equation as:
2πr = nh/mv
Comparing the equation with the equation for circular motion F_c = mv^2/r, we can see that nh/m represents the centripetal force.
Therefore, the radius of the nth orbital is proportional to the square root of n, which corresponds to option 3) n^3/2.
Hence, the correct answer is option 3) n^3/2.
Attention NEET Students!
To make sure you are not studying endlessly, EduRev has designed NEET study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in NEET.

|
Explore Courses for NEET exam
|

|
Similar NEET Doubts
Orbits of a particle moving in a circle are such that the perimeter of the orbit equals an integer number of de-broglie wavelengths of the particle.For a charged particle moving in a plane perpendicular to a magnetic field,the radius of the nth orbital will be therefore proportional to. 1)n^2. 2)n. 3)n^3/2. 4)n^1/4.?
Question Description
Orbits of a particle moving in a circle are such that the perimeter of the orbit equals an integer number of de-broglie wavelengths of the particle.For a charged particle moving in a plane perpendicular to a magnetic field,the radius of the nth orbital will be therefore proportional to. 1)n^2. 2)n. 3)n^3/2. 4)n^1/4.? for NEET 2024 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about Orbits of a particle moving in a circle are such that the perimeter of the orbit equals an integer number of de-broglie wavelengths of the particle.For a charged particle moving in a plane perpendicular to a magnetic field,the radius of the nth orbital will be therefore proportional to. 1)n^2. 2)n. 3)n^3/2. 4)n^1/4.? covers all topics & solutions for NEET 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Orbits of a particle moving in a circle are such that the perimeter of the orbit equals an integer number of de-broglie wavelengths of the particle.For a charged particle moving in a plane perpendicular to a magnetic field,the radius of the nth orbital will be therefore proportional to. 1)n^2. 2)n. 3)n^3/2. 4)n^1/4.?.
Orbits of a particle moving in a circle are such that the perimeter of the orbit equals an integer number of de-broglie wavelengths of the particle.For a charged particle moving in a plane perpendicular to a magnetic field,the radius of the nth orbital will be therefore proportional to. 1)n^2. 2)n. 3)n^3/2. 4)n^1/4.? for NEET 2024 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about Orbits of a particle moving in a circle are such that the perimeter of the orbit equals an integer number of de-broglie wavelengths of the particle.For a charged particle moving in a plane perpendicular to a magnetic field,the radius of the nth orbital will be therefore proportional to. 1)n^2. 2)n. 3)n^3/2. 4)n^1/4.? covers all topics & solutions for NEET 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Orbits of a particle moving in a circle are such that the perimeter of the orbit equals an integer number of de-broglie wavelengths of the particle.For a charged particle moving in a plane perpendicular to a magnetic field,the radius of the nth orbital will be therefore proportional to. 1)n^2. 2)n. 3)n^3/2. 4)n^1/4.?.
Solutions for Orbits of a particle moving in a circle are such that the perimeter of the orbit equals an integer number of de-broglie wavelengths of the particle.For a charged particle moving in a plane perpendicular to a magnetic field,the radius of the nth orbital will be therefore proportional to. 1)n^2. 2)n. 3)n^3/2. 4)n^1/4.? in English & in Hindi are available as part of our courses for NEET.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.
Here you can find the meaning of Orbits of a particle moving in a circle are such that the perimeter of the orbit equals an integer number of de-broglie wavelengths of the particle.For a charged particle moving in a plane perpendicular to a magnetic field,the radius of the nth orbital will be therefore proportional to. 1)n^2. 2)n. 3)n^3/2. 4)n^1/4.? defined & explained in the simplest way possible. Besides giving the explanation of
Orbits of a particle moving in a circle are such that the perimeter of the orbit equals an integer number of de-broglie wavelengths of the particle.For a charged particle moving in a plane perpendicular to a magnetic field,the radius of the nth orbital will be therefore proportional to. 1)n^2. 2)n. 3)n^3/2. 4)n^1/4.?, a detailed solution for Orbits of a particle moving in a circle are such that the perimeter of the orbit equals an integer number of de-broglie wavelengths of the particle.For a charged particle moving in a plane perpendicular to a magnetic field,the radius of the nth orbital will be therefore proportional to. 1)n^2. 2)n. 3)n^3/2. 4)n^1/4.? has been provided alongside types of Orbits of a particle moving in a circle are such that the perimeter of the orbit equals an integer number of de-broglie wavelengths of the particle.For a charged particle moving in a plane perpendicular to a magnetic field,the radius of the nth orbital will be therefore proportional to. 1)n^2. 2)n. 3)n^3/2. 4)n^1/4.? theory, EduRev gives you an
ample number of questions to practice Orbits of a particle moving in a circle are such that the perimeter of the orbit equals an integer number of de-broglie wavelengths of the particle.For a charged particle moving in a plane perpendicular to a magnetic field,the radius of the nth orbital will be therefore proportional to. 1)n^2. 2)n. 3)n^3/2. 4)n^1/4.? tests, examples and also practice NEET tests.

|
Explore Courses for NEET exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.

























