Class 10 Exam > Class 10 Questions > Draw a triangle ABC in which AB=3.8cm and ang...
Start Learning for Free
Draw a triangle ABC in which AB=3.8cm and angle B =60 median = 3.6cm and another triangle AB'C similar to the first such that AB'=(4/3)AB?
Verified Answer
Draw a triangle ABC in which AB=3.8cm and angle B =60 median = 3.6cm a...
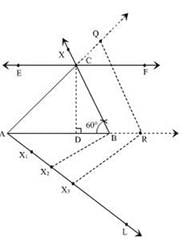
Draw a line segment AB of length 5cm.
Taking B as point Construct an angle of measure 60o using a compass.
Name the angle as angle ABX.
Draw a line EF at a height of 3 cm such that it is parallel to the line segment AB. It must intersect ray BX at point C. Now join AC.
Draw CD perpendicular to AB. CD is altitude of triangle ABC having height 3cm.
 This question is part of UPSC exam. View all Class 10 courses
This question is part of UPSC exam. View all Class 10 courses
Most Upvoted Answer
Draw a triangle ABC in which AB=3.8cm and angle B =60 median = 3.6cm a...
Triangle ABC:
To draw triangle ABC, we need to follow the given information:
- Side AB = 3.8cm
- Angle B = 60°
- Median = 3.6cm
Construction Steps:
1. Draw a line segment AB of length 3.8cm.
2. At point A, draw a ray AX making an angle of 60° with AB.
3. Using a compass, open it to a length of 1.8cm (half of the given median length) and draw an arc from point X intersecting the ray AX at point Y.
4. Join points B and Y. This line segment BY will be the median of triangle ABC.
Triangle AB'C:
To draw triangle AB'C, we need to follow the given information:
- Side AB' = (4/3)AB
Construction Steps:
1. Draw a line segment AB of length 3.8cm.
2. Multiply the length of AB by (4/3) to obtain AB'.
AB' = (4/3) * 3.8cm = 5.07cm
3. At point A, draw a ray AX making an angle of 60° with AB.
4. Using a compass, open it to a length of 5.07cm and draw an arc from point X intersecting the ray AX at point Y.
5. Join points B and Y. This line segment BY will be the median of triangle AB'C.
Explanation:
- Triangle ABC is drawn using the given side length AB = 3.8cm and angle B = 60°. The median BY is constructed by drawing an arc from the midpoint of AB to the opposite vertex.
- Triangle AB'C is similar to triangle ABC because both triangles have the same angle measures. To draw AB'C, we multiply the length of AB by (4/3) to obtain the length of AB'. Using this length, we construct triangle AB'C by following the same steps as triangle ABC.
- The triangles ABC and AB'C are similar because they have the same angle measures. This means that corresponding sides of the triangles are in proportion. In this case, AB' is (4/3) times the length of AB, which satisfies the conditions for similarity.
Note:
- The given measurements and construction steps are approximate and can be adjusted according to the available tools and precision required.
To draw triangle ABC, we need to follow the given information:
- Side AB = 3.8cm
- Angle B = 60°
- Median = 3.6cm
Construction Steps:
1. Draw a line segment AB of length 3.8cm.
2. At point A, draw a ray AX making an angle of 60° with AB.
3. Using a compass, open it to a length of 1.8cm (half of the given median length) and draw an arc from point X intersecting the ray AX at point Y.
4. Join points B and Y. This line segment BY will be the median of triangle ABC.
Triangle AB'C:
To draw triangle AB'C, we need to follow the given information:
- Side AB' = (4/3)AB
Construction Steps:
1. Draw a line segment AB of length 3.8cm.
2. Multiply the length of AB by (4/3) to obtain AB'.
AB' = (4/3) * 3.8cm = 5.07cm
3. At point A, draw a ray AX making an angle of 60° with AB.
4. Using a compass, open it to a length of 5.07cm and draw an arc from point X intersecting the ray AX at point Y.
5. Join points B and Y. This line segment BY will be the median of triangle AB'C.
Explanation:
- Triangle ABC is drawn using the given side length AB = 3.8cm and angle B = 60°. The median BY is constructed by drawing an arc from the midpoint of AB to the opposite vertex.
- Triangle AB'C is similar to triangle ABC because both triangles have the same angle measures. To draw AB'C, we multiply the length of AB by (4/3) to obtain the length of AB'. Using this length, we construct triangle AB'C by following the same steps as triangle ABC.
- The triangles ABC and AB'C are similar because they have the same angle measures. This means that corresponding sides of the triangles are in proportion. In this case, AB' is (4/3) times the length of AB, which satisfies the conditions for similarity.
Note:
- The given measurements and construction steps are approximate and can be adjusted according to the available tools and precision required.

|
Explore Courses for Class 10 exam
|

|
Similar Class 10 Doubts
Draw a triangle ABC in which AB=3.8cm and angle B =60 median = 3.6cm and another triangle AB'C similar to the first such that AB'=(4/3)AB?
Question Description
Draw a triangle ABC in which AB=3.8cm and angle B =60 median = 3.6cm and another triangle AB'C similar to the first such that AB'=(4/3)AB? for Class 10 2025 is part of Class 10 preparation. The Question and answers have been prepared according to the Class 10 exam syllabus. Information about Draw a triangle ABC in which AB=3.8cm and angle B =60 median = 3.6cm and another triangle AB'C similar to the first such that AB'=(4/3)AB? covers all topics & solutions for Class 10 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Draw a triangle ABC in which AB=3.8cm and angle B =60 median = 3.6cm and another triangle AB'C similar to the first such that AB'=(4/3)AB?.
Draw a triangle ABC in which AB=3.8cm and angle B =60 median = 3.6cm and another triangle AB'C similar to the first such that AB'=(4/3)AB? for Class 10 2025 is part of Class 10 preparation. The Question and answers have been prepared according to the Class 10 exam syllabus. Information about Draw a triangle ABC in which AB=3.8cm and angle B =60 median = 3.6cm and another triangle AB'C similar to the first such that AB'=(4/3)AB? covers all topics & solutions for Class 10 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Draw a triangle ABC in which AB=3.8cm and angle B =60 median = 3.6cm and another triangle AB'C similar to the first such that AB'=(4/3)AB?.
Solutions for Draw a triangle ABC in which AB=3.8cm and angle B =60 median = 3.6cm and another triangle AB'C similar to the first such that AB'=(4/3)AB? in English & in Hindi are available as part of our courses for Class 10.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.
Here you can find the meaning of Draw a triangle ABC in which AB=3.8cm and angle B =60 median = 3.6cm and another triangle AB'C similar to the first such that AB'=(4/3)AB? defined & explained in the simplest way possible. Besides giving the explanation of
Draw a triangle ABC in which AB=3.8cm and angle B =60 median = 3.6cm and another triangle AB'C similar to the first such that AB'=(4/3)AB?, a detailed solution for Draw a triangle ABC in which AB=3.8cm and angle B =60 median = 3.6cm and another triangle AB'C similar to the first such that AB'=(4/3)AB? has been provided alongside types of Draw a triangle ABC in which AB=3.8cm and angle B =60 median = 3.6cm and another triangle AB'C similar to the first such that AB'=(4/3)AB? theory, EduRev gives you an
ample number of questions to practice Draw a triangle ABC in which AB=3.8cm and angle B =60 median = 3.6cm and another triangle AB'C similar to the first such that AB'=(4/3)AB? tests, examples and also practice Class 10 tests.

|
Explore Courses for Class 10 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
























