GATE Exam > GATE Questions > A square plate of dimension (axa) rigidly hel...
Start Learning for Free
A square plate of dimension (axa) rigidly held along its 3 edge and force to move alone it's 4th edge. If temperature is increased by T degree Celsius then expansion along the 4th edge will be?
Verified Answer
A square plate of dimension (axa) rigidly held along its 3 edge and fo...
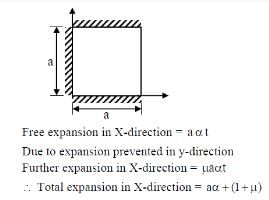
 This question is part of UPSC exam. View all GATE courses
This question is part of UPSC exam. View all GATE courses
Most Upvoted Answer
A square plate of dimension (axa) rigidly held along its 3 edge and fo...
Expansion of a Square Plate
When a square plate is subjected to a change in temperature, it undergoes thermal expansion. In this scenario, the plate is rigidly held along three edges and forced to move along its fourth edge. We need to determine the expansion along the fourth edge when the temperature increases by T degrees Celsius.
Understanding Thermal Expansion
When an object undergoes a change in temperature, its atoms and molecules vibrate with increased energy. This increased energy causes them to move further apart, leading to an expansion of the object. The amount of expansion depends on the material's coefficient of linear expansion (α), which is a measure of how much the material expands per unit change in temperature.
Expansion Along the Fourth Edge
Since the square plate is rigidly held along three edges, it can only expand along its fourth edge. To calculate the expansion along the fourth edge, we need to consider the coefficient of linear expansion of the material and the original dimensions of the plate.
Let's assume the original length of the fourth edge is 'a' and the coefficient of linear expansion is 'α'. The change in length (∆L) along the fourth edge can be calculated using the formula:
∆L = α * L * ∆T
Where:
∆L = Change in length along the fourth edge
α = Coefficient of linear expansion
L = Original length of the fourth edge
∆T = Change in temperature (T degrees Celsius)
Calculating the Expansion
In this scenario, the original dimension of the square plate is 'a x a'. Since it is a square, all sides are equal in length. Therefore, the original length of the fourth edge is 'a'.
Using the formula mentioned above, the expansion along the fourth edge can be calculated as:
∆L = α * a * ∆T
The expansion (∆L) will depend on the coefficient of linear expansion (α) of the material and the change in temperature (∆T).
When a square plate is subjected to a change in temperature, it undergoes thermal expansion. In this scenario, the plate is rigidly held along three edges and forced to move along its fourth edge. We need to determine the expansion along the fourth edge when the temperature increases by T degrees Celsius.
Understanding Thermal Expansion
When an object undergoes a change in temperature, its atoms and molecules vibrate with increased energy. This increased energy causes them to move further apart, leading to an expansion of the object. The amount of expansion depends on the material's coefficient of linear expansion (α), which is a measure of how much the material expands per unit change in temperature.
Expansion Along the Fourth Edge
Since the square plate is rigidly held along three edges, it can only expand along its fourth edge. To calculate the expansion along the fourth edge, we need to consider the coefficient of linear expansion of the material and the original dimensions of the plate.
Let's assume the original length of the fourth edge is 'a' and the coefficient of linear expansion is 'α'. The change in length (∆L) along the fourth edge can be calculated using the formula:
∆L = α * L * ∆T
Where:
∆L = Change in length along the fourth edge
α = Coefficient of linear expansion
L = Original length of the fourth edge
∆T = Change in temperature (T degrees Celsius)
Calculating the Expansion
In this scenario, the original dimension of the square plate is 'a x a'. Since it is a square, all sides are equal in length. Therefore, the original length of the fourth edge is 'a'.
Using the formula mentioned above, the expansion along the fourth edge can be calculated as:
∆L = α * a * ∆T
The expansion (∆L) will depend on the coefficient of linear expansion (α) of the material and the change in temperature (∆T).

|
Explore Courses for GATE exam
|

|
Similar GATE Doubts
A square plate of dimension (axa) rigidly held along its 3 edge and force to move alone it's 4th edge. If temperature is increased by T degree Celsius then expansion along the 4th edge will be?
Question Description
A square plate of dimension (axa) rigidly held along its 3 edge and force to move alone it's 4th edge. If temperature is increased by T degree Celsius then expansion along the 4th edge will be? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about A square plate of dimension (axa) rigidly held along its 3 edge and force to move alone it's 4th edge. If temperature is increased by T degree Celsius then expansion along the 4th edge will be? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A square plate of dimension (axa) rigidly held along its 3 edge and force to move alone it's 4th edge. If temperature is increased by T degree Celsius then expansion along the 4th edge will be?.
A square plate of dimension (axa) rigidly held along its 3 edge and force to move alone it's 4th edge. If temperature is increased by T degree Celsius then expansion along the 4th edge will be? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about A square plate of dimension (axa) rigidly held along its 3 edge and force to move alone it's 4th edge. If temperature is increased by T degree Celsius then expansion along the 4th edge will be? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A square plate of dimension (axa) rigidly held along its 3 edge and force to move alone it's 4th edge. If temperature is increased by T degree Celsius then expansion along the 4th edge will be?.
Solutions for A square plate of dimension (axa) rigidly held along its 3 edge and force to move alone it's 4th edge. If temperature is increased by T degree Celsius then expansion along the 4th edge will be? in English & in Hindi are available as part of our courses for GATE.
Download more important topics, notes, lectures and mock test series for GATE Exam by signing up for free.
Here you can find the meaning of A square plate of dimension (axa) rigidly held along its 3 edge and force to move alone it's 4th edge. If temperature is increased by T degree Celsius then expansion along the 4th edge will be? defined & explained in the simplest way possible. Besides giving the explanation of
A square plate of dimension (axa) rigidly held along its 3 edge and force to move alone it's 4th edge. If temperature is increased by T degree Celsius then expansion along the 4th edge will be?, a detailed solution for A square plate of dimension (axa) rigidly held along its 3 edge and force to move alone it's 4th edge. If temperature is increased by T degree Celsius then expansion along the 4th edge will be? has been provided alongside types of A square plate of dimension (axa) rigidly held along its 3 edge and force to move alone it's 4th edge. If temperature is increased by T degree Celsius then expansion along the 4th edge will be? theory, EduRev gives you an
ample number of questions to practice A square plate of dimension (axa) rigidly held along its 3 edge and force to move alone it's 4th edge. If temperature is increased by T degree Celsius then expansion along the 4th edge will be? tests, examples and also practice GATE tests.

|
Explore Courses for GATE exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.














