NEET Exam > NEET Questions > A solid sphere is rotating freely about its s...
Start Learning for Free
A solid sphere is rotating freely about its symmetryaxis in free space. The radius of the sphere isincreased keeping its mass same. Which of thefollowing physical quantities would remain constantfor the sphere ?
- a)Angular velocity
- b)Moment of inertia
- c)Rotational kinetic energy
- d)Angular momentum
Correct answer is option 'D'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A solid sphere is rotating freely about its symmetryaxis in free space...
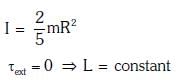
Most Upvoted Answer
A solid sphere is rotating freely about its symmetryaxis in free space...
Angular momentum is conserved for a rotating object
- Angular momentum is a fundamental property of a rotating object and is defined as the product of the moment of inertia and the angular velocity.
- The moment of inertia depends on the distribution of mass in the object and the axis of rotation.
- When the radius of the sphere is increased while keeping its mass the same, the moment of inertia changes.
- The moment of inertia of a solid sphere is given by the equation I = (2/5) * m * r^2, where m is the mass of the sphere and r is the radius.
- As the radius is increased, the moment of inertia also increases. This means that the distribution of mass in the sphere has changed, resulting in a different moment of inertia.
- However, the mass of the sphere remains the same, so its angular momentum must remain constant.
Explanation of the other options:
a) Angular velocity: The angular velocity of the sphere is not constant because the radius is changed. The angular velocity is given by the equation ω = v/r, where v is the linear velocity and r is the radius. Since the radius is increased, the angular velocity will decrease to maintain the same linear velocity.
b) Moment of inertia: The moment of inertia changes when the radius of the sphere is increased. The moment of inertia is a measure of an object's resistance to changes in its rotational motion. When the mass is kept the same but the radius is increased, the distribution of mass changes, resulting in a different moment of inertia.
c) Rotational kinetic energy: The rotational kinetic energy of a rotating object is given by the equation KE = (1/2) * I * ω^2, where I is the moment of inertia and ω is the angular velocity. Since the moment of inertia changes when the radius is increased, the rotational kinetic energy will also change.
d) Angular momentum: As mentioned earlier, the angular momentum of the sphere remains constant because the mass is kept the same. The angular momentum is given by the equation L = I * ω, where I is the moment of inertia and ω is the angular velocity. Since the mass is the same, the moment of inertia changes to compensate for the change in the radius, resulting in a constant angular momentum.
- Angular momentum is a fundamental property of a rotating object and is defined as the product of the moment of inertia and the angular velocity.
- The moment of inertia depends on the distribution of mass in the object and the axis of rotation.
- When the radius of the sphere is increased while keeping its mass the same, the moment of inertia changes.
- The moment of inertia of a solid sphere is given by the equation I = (2/5) * m * r^2, where m is the mass of the sphere and r is the radius.
- As the radius is increased, the moment of inertia also increases. This means that the distribution of mass in the sphere has changed, resulting in a different moment of inertia.
- However, the mass of the sphere remains the same, so its angular momentum must remain constant.
Explanation of the other options:
a) Angular velocity: The angular velocity of the sphere is not constant because the radius is changed. The angular velocity is given by the equation ω = v/r, where v is the linear velocity and r is the radius. Since the radius is increased, the angular velocity will decrease to maintain the same linear velocity.
b) Moment of inertia: The moment of inertia changes when the radius of the sphere is increased. The moment of inertia is a measure of an object's resistance to changes in its rotational motion. When the mass is kept the same but the radius is increased, the distribution of mass changes, resulting in a different moment of inertia.
c) Rotational kinetic energy: The rotational kinetic energy of a rotating object is given by the equation KE = (1/2) * I * ω^2, where I is the moment of inertia and ω is the angular velocity. Since the moment of inertia changes when the radius is increased, the rotational kinetic energy will also change.
d) Angular momentum: As mentioned earlier, the angular momentum of the sphere remains constant because the mass is kept the same. The angular momentum is given by the equation L = I * ω, where I is the moment of inertia and ω is the angular velocity. Since the mass is the same, the moment of inertia changes to compensate for the change in the radius, resulting in a constant angular momentum.
Free Test
FREE
| Start Free Test |
Community Answer
A solid sphere is rotating freely about its symmetryaxis in free space...
L=iw so L doesn't depend on mass
Attention NEET Students!
To make sure you are not studying endlessly, EduRev has designed NEET study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in NEET.

|
Explore Courses for NEET exam
|

|
A solid sphere is rotating freely about its symmetryaxis in free space. The radius of the sphere isincreased keeping its mass same. Which of thefollowing physical quantities would remain constantfor the sphere ?a)Angular velocityb)Moment of inertiac)Rotational kinetic energyd)Angular momentumCorrect answer is option 'D'. Can you explain this answer?
Question Description
A solid sphere is rotating freely about its symmetryaxis in free space. The radius of the sphere isincreased keeping its mass same. Which of thefollowing physical quantities would remain constantfor the sphere ?a)Angular velocityb)Moment of inertiac)Rotational kinetic energyd)Angular momentumCorrect answer is option 'D'. Can you explain this answer? for NEET 2024 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about A solid sphere is rotating freely about its symmetryaxis in free space. The radius of the sphere isincreased keeping its mass same. Which of thefollowing physical quantities would remain constantfor the sphere ?a)Angular velocityb)Moment of inertiac)Rotational kinetic energyd)Angular momentumCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for NEET 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A solid sphere is rotating freely about its symmetryaxis in free space. The radius of the sphere isincreased keeping its mass same. Which of thefollowing physical quantities would remain constantfor the sphere ?a)Angular velocityb)Moment of inertiac)Rotational kinetic energyd)Angular momentumCorrect answer is option 'D'. Can you explain this answer?.
A solid sphere is rotating freely about its symmetryaxis in free space. The radius of the sphere isincreased keeping its mass same. Which of thefollowing physical quantities would remain constantfor the sphere ?a)Angular velocityb)Moment of inertiac)Rotational kinetic energyd)Angular momentumCorrect answer is option 'D'. Can you explain this answer? for NEET 2024 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about A solid sphere is rotating freely about its symmetryaxis in free space. The radius of the sphere isincreased keeping its mass same. Which of thefollowing physical quantities would remain constantfor the sphere ?a)Angular velocityb)Moment of inertiac)Rotational kinetic energyd)Angular momentumCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for NEET 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A solid sphere is rotating freely about its symmetryaxis in free space. The radius of the sphere isincreased keeping its mass same. Which of thefollowing physical quantities would remain constantfor the sphere ?a)Angular velocityb)Moment of inertiac)Rotational kinetic energyd)Angular momentumCorrect answer is option 'D'. Can you explain this answer?.
Solutions for A solid sphere is rotating freely about its symmetryaxis in free space. The radius of the sphere isincreased keeping its mass same. Which of thefollowing physical quantities would remain constantfor the sphere ?a)Angular velocityb)Moment of inertiac)Rotational kinetic energyd)Angular momentumCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for NEET.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.
Here you can find the meaning of A solid sphere is rotating freely about its symmetryaxis in free space. The radius of the sphere isincreased keeping its mass same. Which of thefollowing physical quantities would remain constantfor the sphere ?a)Angular velocityb)Moment of inertiac)Rotational kinetic energyd)Angular momentumCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A solid sphere is rotating freely about its symmetryaxis in free space. The radius of the sphere isincreased keeping its mass same. Which of thefollowing physical quantities would remain constantfor the sphere ?a)Angular velocityb)Moment of inertiac)Rotational kinetic energyd)Angular momentumCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for A solid sphere is rotating freely about its symmetryaxis in free space. The radius of the sphere isincreased keeping its mass same. Which of thefollowing physical quantities would remain constantfor the sphere ?a)Angular velocityb)Moment of inertiac)Rotational kinetic energyd)Angular momentumCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of A solid sphere is rotating freely about its symmetryaxis in free space. The radius of the sphere isincreased keeping its mass same. Which of thefollowing physical quantities would remain constantfor the sphere ?a)Angular velocityb)Moment of inertiac)Rotational kinetic energyd)Angular momentumCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A solid sphere is rotating freely about its symmetryaxis in free space. The radius of the sphere isincreased keeping its mass same. Which of thefollowing physical quantities would remain constantfor the sphere ?a)Angular velocityb)Moment of inertiac)Rotational kinetic energyd)Angular momentumCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice NEET tests.

|
Explore Courses for NEET exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.






















