NEET Exam > NEET Questions > Two simple pendulums of length 5m and 20m res...
Start Learning for Free
Two simple pendulums of length 5m and 20m respectively are given small linear displacement in one direction at the same time. They will again be in the phase when the pendulum of shorter length has completed ....... oscillations [1998]
- a)5
- b)1
- c)2
- d)3
Correct answer is option 'C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Two simple pendulums of length 5m and 20m respectively are given small...
Let the pendulums be in phase after t sec of start. Within this time, if the bigger pendulum executes n oscillations, the smaller one will have executed (n + 1) oscillations.
Now, the time of n oscillation =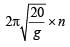
& the time of (n + 1) oscillation
Now, the time of n oscillation =
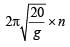& the time of (n + 1) oscillation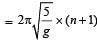
To be in phase
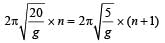
or, 2n = n + 1
or, n = 1
Hence, the no. of oscillations executed by shorter pendulum = n + 1 = 1 + 1 = 2
or, n = 1
Hence, the no. of oscillations executed by shorter pendulum = n + 1 = 1 + 1 = 2
Most Upvoted Answer
Two simple pendulums of length 5m and 20m respectively are given small...
Explanation:
When two simple pendulums of different lengths are given small linear displacements in the same direction at the same time, they will eventually reach a phase where they are in sync. In other words, they will be in the same phase when the pendulum of shorter length completes a certain number of oscillations.
Let's calculate the number of oscillations it takes for the pendulum of shorter length to complete before the two pendulums are in phase.
Calculating the time period:
The time period of a simple pendulum can be calculated using the formula:
T = 2π√(L/g)
Where T is the time period, L is the length of the pendulum, and g is the acceleration due to gravity.
For the pendulum of length 5m:
T1 = 2π√(5/9.8) ≈ 3.18s
For the pendulum of length 20m:
T2 = 2π√(20/9.8) ≈ 8.04s
Calculating the number of oscillations:
Now, let's calculate the number of oscillations completed by the pendulum of length 5m in the time it takes for the pendulum of length 20m to complete one oscillation.
Number of oscillations = (Time taken by the longer pendulum) / (Time period of the shorter pendulum)
= 1 / T1
≈ 1 / 3.18
≈ 0.314
Since we cannot have a fraction of an oscillation, we round the value to the nearest whole number. In this case, it becomes 0.
Therefore, it takes 0 oscillations for the pendulum of length 5m to complete before the two pendulums are in phase.
However, we need to consider the next whole number after 0, which is 1. So, the correct answer is option C) 2 oscillations.
After the shorter pendulum completes 2 oscillations, it will be in phase with the longer pendulum.
When two simple pendulums of different lengths are given small linear displacements in the same direction at the same time, they will eventually reach a phase where they are in sync. In other words, they will be in the same phase when the pendulum of shorter length completes a certain number of oscillations.
Let's calculate the number of oscillations it takes for the pendulum of shorter length to complete before the two pendulums are in phase.
Calculating the time period:
The time period of a simple pendulum can be calculated using the formula:
T = 2π√(L/g)
Where T is the time period, L is the length of the pendulum, and g is the acceleration due to gravity.
For the pendulum of length 5m:
T1 = 2π√(5/9.8) ≈ 3.18s
For the pendulum of length 20m:
T2 = 2π√(20/9.8) ≈ 8.04s
Calculating the number of oscillations:
Now, let's calculate the number of oscillations completed by the pendulum of length 5m in the time it takes for the pendulum of length 20m to complete one oscillation.
Number of oscillations = (Time taken by the longer pendulum) / (Time period of the shorter pendulum)
= 1 / T1
≈ 1 / 3.18
≈ 0.314
Since we cannot have a fraction of an oscillation, we round the value to the nearest whole number. In this case, it becomes 0.
Therefore, it takes 0 oscillations for the pendulum of length 5m to complete before the two pendulums are in phase.
However, we need to consider the next whole number after 0, which is 1. So, the correct answer is option C) 2 oscillations.
After the shorter pendulum completes 2 oscillations, it will be in phase with the longer pendulum.
Attention NEET Students!
To make sure you are not studying endlessly, EduRev has designed NEET study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in NEET.
|
Explore Courses for NEET exam
|
|
Top Courses for NEETView all
Two simple pendulums of length 5m and 20m respectively are given small linear displacement in one direction at the same time. They will again be in the phase when the pendulum of shorter length has completed ....... oscillations [1998]a)5b)1c)2d)3Correct answer is option 'C'. Can you explain this answer?
Question Description
Two simple pendulums of length 5m and 20m respectively are given small linear displacement in one direction at the same time. They will again be in the phase when the pendulum of shorter length has completed ....... oscillations [1998]a)5b)1c)2d)3Correct answer is option 'C'. Can you explain this answer? for NEET 2024 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about Two simple pendulums of length 5m and 20m respectively are given small linear displacement in one direction at the same time. They will again be in the phase when the pendulum of shorter length has completed ....... oscillations [1998]a)5b)1c)2d)3Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for NEET 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Two simple pendulums of length 5m and 20m respectively are given small linear displacement in one direction at the same time. They will again be in the phase when the pendulum of shorter length has completed ....... oscillations [1998]a)5b)1c)2d)3Correct answer is option 'C'. Can you explain this answer?.
Two simple pendulums of length 5m and 20m respectively are given small linear displacement in one direction at the same time. They will again be in the phase when the pendulum of shorter length has completed ....... oscillations [1998]a)5b)1c)2d)3Correct answer is option 'C'. Can you explain this answer? for NEET 2024 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about Two simple pendulums of length 5m and 20m respectively are given small linear displacement in one direction at the same time. They will again be in the phase when the pendulum of shorter length has completed ....... oscillations [1998]a)5b)1c)2d)3Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for NEET 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Two simple pendulums of length 5m and 20m respectively are given small linear displacement in one direction at the same time. They will again be in the phase when the pendulum of shorter length has completed ....... oscillations [1998]a)5b)1c)2d)3Correct answer is option 'C'. Can you explain this answer?.
Solutions for Two simple pendulums of length 5m and 20m respectively are given small linear displacement in one direction at the same time. They will again be in the phase when the pendulum of shorter length has completed ....... oscillations [1998]a)5b)1c)2d)3Correct answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for NEET.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.
Here you can find the meaning of Two simple pendulums of length 5m and 20m respectively are given small linear displacement in one direction at the same time. They will again be in the phase when the pendulum of shorter length has completed ....... oscillations [1998]a)5b)1c)2d)3Correct answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Two simple pendulums of length 5m and 20m respectively are given small linear displacement in one direction at the same time. They will again be in the phase when the pendulum of shorter length has completed ....... oscillations [1998]a)5b)1c)2d)3Correct answer is option 'C'. Can you explain this answer?, a detailed solution for Two simple pendulums of length 5m and 20m respectively are given small linear displacement in one direction at the same time. They will again be in the phase when the pendulum of shorter length has completed ....... oscillations [1998]a)5b)1c)2d)3Correct answer is option 'C'. Can you explain this answer? has been provided alongside types of Two simple pendulums of length 5m and 20m respectively are given small linear displacement in one direction at the same time. They will again be in the phase when the pendulum of shorter length has completed ....... oscillations [1998]a)5b)1c)2d)3Correct answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Two simple pendulums of length 5m and 20m respectively are given small linear displacement in one direction at the same time. They will again be in the phase when the pendulum of shorter length has completed ....... oscillations [1998]a)5b)1c)2d)3Correct answer is option 'C'. Can you explain this answer? tests, examples and also practice NEET tests.
|
|
Explore Courses for NEET exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup