Physics Exam > Physics Questions > In a given n-type silicon material, the donar...
Start Learning for Free
In a given n-type silicon material, the donar concentration is 1 atom per 2 * 108 silicon atoms. Assuming that the effective mass of the electron is equal to its true mass. Given that density of atoms in silicon = 5 * 1028 atoms/m3. Which of the following statement is correct.
- a)Mass cannot be determined
- b)Temperature at which fermi level coincides with the edge of the conduction band is 0.14 K
- c)Concentration of donar atoms is 2 x 108 atoms/m3
- d)None o f these
Correct answer is option 'B'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
In a given n-type silicon material, the donar concentration is 1 atom ...
The donor consecration will be calculated first. As there are 1 atoms per 2 x 108 silicon atoms, there will be
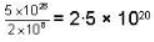
donor atoms per met3. This density of doner
Nd = 2-5 x 1020 per m3
We know that Fermi level will coincides with the edge of conduction band if Nd = Nc, where

with
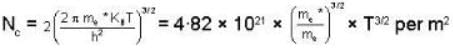
But given that effective mass of the electron is equal to its true mass, i.e.,
me* = me
so that
NC = 4.82 x 1021 x T3/2
Putting it equal to Nd, we get
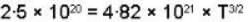
or
T = 0.14 K
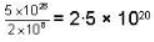
donor atoms per met3. This density of doner
Nd = 2-5 x 1020 per m3
We know that Fermi level will coincides with the edge of conduction band if Nd = Nc, where

with
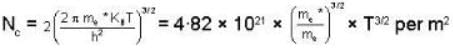
But given that effective mass of the electron is equal to its true mass, i.e.,
me* = me
so that
NC = 4.82 x 1021 x T3/2
Putting it equal to Nd, we get
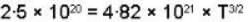
or
T = 0.14 K
Most Upvoted Answer
In a given n-type silicon material, the donar concentration is 1 atom ...
Given information:
- N-type silicon material
- Donor concentration: 1 atom per 2 * 10^8 silicon atoms
- Density of atoms in silicon: 5 * 10^28 atoms/m^3
Explanation:
The given information allows us to calculate the concentration of donor atoms in the silicon material. Let's calculate it step by step.
Step 1: Calculate the number of silicon atoms per unit volume
Given that the density of atoms in silicon is 5 * 10^28 atoms/m^3, we can calculate the number of silicon atoms per unit volume as follows:
Number of silicon atoms per unit volume = density of silicon * volume
Number of silicon atoms per unit volume = (5 * 10^28 atoms/m^3) * (1 m^3)
Number of silicon atoms per unit volume = 5 * 10^28 atoms
Step 2: Calculate the donor atom concentration
Given that there is 1 donor atom per 2 * 10^8 silicon atoms, we can calculate the donor atom concentration as follows:
Donor atom concentration = (1 donor atom / 2 * 10^8 silicon atoms) * (5 * 10^28 silicon atoms)
Donor atom concentration = 0.25 * 10^20 donor atoms
Step 3: Determine the temperature at which the Fermi level coincides with the edge of the conduction band
At absolute zero temperature, the Fermi level lies at the highest occupied energy level in the material. As the temperature increases, some electrons gain enough energy to move from the valence band to the conduction band, creating holes in the valence band.
At a certain temperature, called the Fermi temperature (T_F), the Fermi level aligns with the edge of the conduction band. Beyond this temperature, the Fermi level will be above the conduction band edge, indicating the presence of free electrons in the conduction band.
In the given question, the donor concentration is given, but the Fermi temperature is not directly provided. However, we can deduce from the given information that the Fermi temperature is very low (0.14 K) compared to the usual operating temperatures of silicon-based devices.
Therefore, the correct statement is option 'B': Temperature at which the Fermi level coincides with the edge of the conduction band is 0.14 K.
- N-type silicon material
- Donor concentration: 1 atom per 2 * 10^8 silicon atoms
- Density of atoms in silicon: 5 * 10^28 atoms/m^3
Explanation:
The given information allows us to calculate the concentration of donor atoms in the silicon material. Let's calculate it step by step.
Step 1: Calculate the number of silicon atoms per unit volume
Given that the density of atoms in silicon is 5 * 10^28 atoms/m^3, we can calculate the number of silicon atoms per unit volume as follows:
Number of silicon atoms per unit volume = density of silicon * volume
Number of silicon atoms per unit volume = (5 * 10^28 atoms/m^3) * (1 m^3)
Number of silicon atoms per unit volume = 5 * 10^28 atoms
Step 2: Calculate the donor atom concentration
Given that there is 1 donor atom per 2 * 10^8 silicon atoms, we can calculate the donor atom concentration as follows:
Donor atom concentration = (1 donor atom / 2 * 10^8 silicon atoms) * (5 * 10^28 silicon atoms)
Donor atom concentration = 0.25 * 10^20 donor atoms
Step 3: Determine the temperature at which the Fermi level coincides with the edge of the conduction band
At absolute zero temperature, the Fermi level lies at the highest occupied energy level in the material. As the temperature increases, some electrons gain enough energy to move from the valence band to the conduction band, creating holes in the valence band.
At a certain temperature, called the Fermi temperature (T_F), the Fermi level aligns with the edge of the conduction band. Beyond this temperature, the Fermi level will be above the conduction band edge, indicating the presence of free electrons in the conduction band.
In the given question, the donor concentration is given, but the Fermi temperature is not directly provided. However, we can deduce from the given information that the Fermi temperature is very low (0.14 K) compared to the usual operating temperatures of silicon-based devices.
Therefore, the correct statement is option 'B': Temperature at which the Fermi level coincides with the edge of the conduction band is 0.14 K.

|
Explore Courses for Physics exam
|

|
Similar Physics Doubts
In a given n-type silicon material, the donar concentration is 1 atom per 2 * 108 silicon atoms. Assuming that the effective mass of the electron is equal to its true mass. Given that density of atoms in silicon = 5 * 1028 atoms/m3. Which of the following statement is correct.a)Mass cannot be determinedb)Temperature at which fermi level coincides with the edge of the conduction band is 0.14 Kc)Concentration of donar atoms is 2 x 108 atoms/m3d)None o f theseCorrect answer is option 'B'. Can you explain this answer?
Question Description
In a given n-type silicon material, the donar concentration is 1 atom per 2 * 108 silicon atoms. Assuming that the effective mass of the electron is equal to its true mass. Given that density of atoms in silicon = 5 * 1028 atoms/m3. Which of the following statement is correct.a)Mass cannot be determinedb)Temperature at which fermi level coincides with the edge of the conduction band is 0.14 Kc)Concentration of donar atoms is 2 x 108 atoms/m3d)None o f theseCorrect answer is option 'B'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about In a given n-type silicon material, the donar concentration is 1 atom per 2 * 108 silicon atoms. Assuming that the effective mass of the electron is equal to its true mass. Given that density of atoms in silicon = 5 * 1028 atoms/m3. Which of the following statement is correct.a)Mass cannot be determinedb)Temperature at which fermi level coincides with the edge of the conduction band is 0.14 Kc)Concentration of donar atoms is 2 x 108 atoms/m3d)None o f theseCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for In a given n-type silicon material, the donar concentration is 1 atom per 2 * 108 silicon atoms. Assuming that the effective mass of the electron is equal to its true mass. Given that density of atoms in silicon = 5 * 1028 atoms/m3. Which of the following statement is correct.a)Mass cannot be determinedb)Temperature at which fermi level coincides with the edge of the conduction band is 0.14 Kc)Concentration of donar atoms is 2 x 108 atoms/m3d)None o f theseCorrect answer is option 'B'. Can you explain this answer?.
In a given n-type silicon material, the donar concentration is 1 atom per 2 * 108 silicon atoms. Assuming that the effective mass of the electron is equal to its true mass. Given that density of atoms in silicon = 5 * 1028 atoms/m3. Which of the following statement is correct.a)Mass cannot be determinedb)Temperature at which fermi level coincides with the edge of the conduction band is 0.14 Kc)Concentration of donar atoms is 2 x 108 atoms/m3d)None o f theseCorrect answer is option 'B'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about In a given n-type silicon material, the donar concentration is 1 atom per 2 * 108 silicon atoms. Assuming that the effective mass of the electron is equal to its true mass. Given that density of atoms in silicon = 5 * 1028 atoms/m3. Which of the following statement is correct.a)Mass cannot be determinedb)Temperature at which fermi level coincides with the edge of the conduction band is 0.14 Kc)Concentration of donar atoms is 2 x 108 atoms/m3d)None o f theseCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for In a given n-type silicon material, the donar concentration is 1 atom per 2 * 108 silicon atoms. Assuming that the effective mass of the electron is equal to its true mass. Given that density of atoms in silicon = 5 * 1028 atoms/m3. Which of the following statement is correct.a)Mass cannot be determinedb)Temperature at which fermi level coincides with the edge of the conduction band is 0.14 Kc)Concentration of donar atoms is 2 x 108 atoms/m3d)None o f theseCorrect answer is option 'B'. Can you explain this answer?.
Solutions for In a given n-type silicon material, the donar concentration is 1 atom per 2 * 108 silicon atoms. Assuming that the effective mass of the electron is equal to its true mass. Given that density of atoms in silicon = 5 * 1028 atoms/m3. Which of the following statement is correct.a)Mass cannot be determinedb)Temperature at which fermi level coincides with the edge of the conduction band is 0.14 Kc)Concentration of donar atoms is 2 x 108 atoms/m3d)None o f theseCorrect answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of In a given n-type silicon material, the donar concentration is 1 atom per 2 * 108 silicon atoms. Assuming that the effective mass of the electron is equal to its true mass. Given that density of atoms in silicon = 5 * 1028 atoms/m3. Which of the following statement is correct.a)Mass cannot be determinedb)Temperature at which fermi level coincides with the edge of the conduction band is 0.14 Kc)Concentration of donar atoms is 2 x 108 atoms/m3d)None o f theseCorrect answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
In a given n-type silicon material, the donar concentration is 1 atom per 2 * 108 silicon atoms. Assuming that the effective mass of the electron is equal to its true mass. Given that density of atoms in silicon = 5 * 1028 atoms/m3. Which of the following statement is correct.a)Mass cannot be determinedb)Temperature at which fermi level coincides with the edge of the conduction band is 0.14 Kc)Concentration of donar atoms is 2 x 108 atoms/m3d)None o f theseCorrect answer is option 'B'. Can you explain this answer?, a detailed solution for In a given n-type silicon material, the donar concentration is 1 atom per 2 * 108 silicon atoms. Assuming that the effective mass of the electron is equal to its true mass. Given that density of atoms in silicon = 5 * 1028 atoms/m3. Which of the following statement is correct.a)Mass cannot be determinedb)Temperature at which fermi level coincides with the edge of the conduction band is 0.14 Kc)Concentration of donar atoms is 2 x 108 atoms/m3d)None o f theseCorrect answer is option 'B'. Can you explain this answer? has been provided alongside types of In a given n-type silicon material, the donar concentration is 1 atom per 2 * 108 silicon atoms. Assuming that the effective mass of the electron is equal to its true mass. Given that density of atoms in silicon = 5 * 1028 atoms/m3. Which of the following statement is correct.a)Mass cannot be determinedb)Temperature at which fermi level coincides with the edge of the conduction band is 0.14 Kc)Concentration of donar atoms is 2 x 108 atoms/m3d)None o f theseCorrect answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice In a given n-type silicon material, the donar concentration is 1 atom per 2 * 108 silicon atoms. Assuming that the effective mass of the electron is equal to its true mass. Given that density of atoms in silicon = 5 * 1028 atoms/m3. Which of the following statement is correct.a)Mass cannot be determinedb)Temperature at which fermi level coincides with the edge of the conduction band is 0.14 Kc)Concentration of donar atoms is 2 x 108 atoms/m3d)None o f theseCorrect answer is option 'B'. Can you explain this answer? tests, examples and also practice Physics tests.

|
Explore Courses for Physics exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















