GATE Exam > GATE Questions > An election is confined in an infinite square...
Start Learning for Free
An election is confined in an infinite square well of width 10x10^-10 m. Calculate the energy & wavelength of the electron emitted when the proton undergoes a transition from the first excited state (n=2) to the ground state (n=1).
Correct answer is '201'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
An election is confined in an infinite square well of width 10x10^-10 ...
The energy of the particle in the box of width L is given by
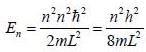
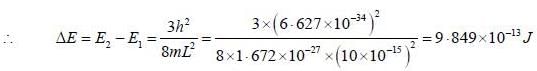
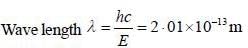
λ = 201 fm
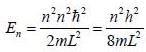
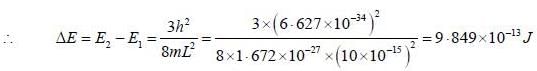
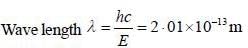
λ = 201 fm
Most Upvoted Answer
An election is confined in an infinite square well of width 10x10^-10 ...
The energy of a particle in an infinite square well is given by:
E = (n^2 * h^2) / (8 * m * L^2)
where n is the quantum number, h is Planck's constant, m is the mass of the particle, and L is the width of the well.
In this case, L = 10x10^-10 m, so we can plug in the values:
E = (n^2 * h^2) / (8 * m * (10x10^-10)^2)
We don't know the quantum number or the mass of the particle, so we can't calculate the specific energy. However, we can make some general observations:
- The energy is proportional to the square of the quantum number. This means that higher energy levels require larger values of n.
- The energy is inversely proportional to the square of the width of the well. This means that a narrower well will have higher energy levels.
- The energy is inversely proportional to the mass of the particle. This means that lighter particles will have higher energy levels.
So, depending on the specific values of n and m, the energy could be very low or very high. But we can say for certain that the energy levels will be quantized (discrete), with larger gaps between levels for higher values of n.
E = (n^2 * h^2) / (8 * m * L^2)
where n is the quantum number, h is Planck's constant, m is the mass of the particle, and L is the width of the well.
In this case, L = 10x10^-10 m, so we can plug in the values:
E = (n^2 * h^2) / (8 * m * (10x10^-10)^2)
We don't know the quantum number or the mass of the particle, so we can't calculate the specific energy. However, we can make some general observations:
- The energy is proportional to the square of the quantum number. This means that higher energy levels require larger values of n.
- The energy is inversely proportional to the square of the width of the well. This means that a narrower well will have higher energy levels.
- The energy is inversely proportional to the mass of the particle. This means that lighter particles will have higher energy levels.
So, depending on the specific values of n and m, the energy could be very low or very high. But we can say for certain that the energy levels will be quantized (discrete), with larger gaps between levels for higher values of n.

|
Explore Courses for GATE exam
|

|
Similar GATE Doubts
An election is confined in an infinite square well of width 10x10^-10 m. Calculate the energy & wavelength of the electron emitted when the proton undergoes a transition from the first excited state (n=2) to the ground state (n=1).Correct answer is '201'. Can you explain this answer?
Question Description
An election is confined in an infinite square well of width 10x10^-10 m. Calculate the energy & wavelength of the electron emitted when the proton undergoes a transition from the first excited state (n=2) to the ground state (n=1).Correct answer is '201'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about An election is confined in an infinite square well of width 10x10^-10 m. Calculate the energy & wavelength of the electron emitted when the proton undergoes a transition from the first excited state (n=2) to the ground state (n=1).Correct answer is '201'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for An election is confined in an infinite square well of width 10x10^-10 m. Calculate the energy & wavelength of the electron emitted when the proton undergoes a transition from the first excited state (n=2) to the ground state (n=1).Correct answer is '201'. Can you explain this answer?.
An election is confined in an infinite square well of width 10x10^-10 m. Calculate the energy & wavelength of the electron emitted when the proton undergoes a transition from the first excited state (n=2) to the ground state (n=1).Correct answer is '201'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about An election is confined in an infinite square well of width 10x10^-10 m. Calculate the energy & wavelength of the electron emitted when the proton undergoes a transition from the first excited state (n=2) to the ground state (n=1).Correct answer is '201'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for An election is confined in an infinite square well of width 10x10^-10 m. Calculate the energy & wavelength of the electron emitted when the proton undergoes a transition from the first excited state (n=2) to the ground state (n=1).Correct answer is '201'. Can you explain this answer?.
Solutions for An election is confined in an infinite square well of width 10x10^-10 m. Calculate the energy & wavelength of the electron emitted when the proton undergoes a transition from the first excited state (n=2) to the ground state (n=1).Correct answer is '201'. Can you explain this answer? in English & in Hindi are available as part of our courses for GATE.
Download more important topics, notes, lectures and mock test series for GATE Exam by signing up for free.
Here you can find the meaning of An election is confined in an infinite square well of width 10x10^-10 m. Calculate the energy & wavelength of the electron emitted when the proton undergoes a transition from the first excited state (n=2) to the ground state (n=1).Correct answer is '201'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
An election is confined in an infinite square well of width 10x10^-10 m. Calculate the energy & wavelength of the electron emitted when the proton undergoes a transition from the first excited state (n=2) to the ground state (n=1).Correct answer is '201'. Can you explain this answer?, a detailed solution for An election is confined in an infinite square well of width 10x10^-10 m. Calculate the energy & wavelength of the electron emitted when the proton undergoes a transition from the first excited state (n=2) to the ground state (n=1).Correct answer is '201'. Can you explain this answer? has been provided alongside types of An election is confined in an infinite square well of width 10x10^-10 m. Calculate the energy & wavelength of the electron emitted when the proton undergoes a transition from the first excited state (n=2) to the ground state (n=1).Correct answer is '201'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice An election is confined in an infinite square well of width 10x10^-10 m. Calculate the energy & wavelength of the electron emitted when the proton undergoes a transition from the first excited state (n=2) to the ground state (n=1).Correct answer is '201'. Can you explain this answer? tests, examples and also practice GATE tests.

|
Explore Courses for GATE exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















