GATE Exam > GATE Questions > Consider a charged sphere of radius R with ch...
Start Learning for Free
Consider a charged sphere of radius R with charge density f(r ) = e-r. The gradient vector to the family of equipotential surfaces of this charged surface points
- a)radially inwards
- b)radially outwards
- c)tangentially in the clockwise direction
- d)tangentially in the anti-clockwise direction
Correct answer is option 'B'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Consider a charged sphere of radius R with charge density f(r ) = e-r....
Given, charge density f(r ) = e-r
This density depends only on the radius r and not (θ, φ) of spherical polar coordinates.
Therefore, the equipotential surfaces for this volume charge are spheres of different radii with potential decreasing radially outwards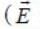
is radially outwards). This means that V (r, θ, φ) decreases with radius. The gradient of a surface is in the direction along the maximum rate o f increase o f the function (here V (r, θ, φ)).
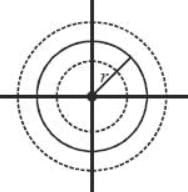
Therefore, gradient of the equipotential surfaces are radially inwards.
This density depends only on the radius r and not (θ, φ) of spherical polar coordinates.
Therefore, the equipotential surfaces for this volume charge are spheres of different radii with potential decreasing radially outwards
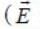is radially outwards). This means that V (r, θ, φ) decreases with radius. The gradient of a surface is in the direction along the maximum rate o f increase o f the function (here V (r, θ, φ)). Therefore, gradient of the equipotential surfaces are radially inwards.
Most Upvoted Answer
Consider a charged sphere of radius R with charge density f(r ) = e-r....
Equipotential Surfaces:
Equipotential surfaces are surfaces in a region where the potential is constant. In the case of a charged sphere, the equipotential surfaces are spherical shells concentric with the sphere.
Charge Density:
The charge density of the sphere is given by f(r) = e^(-r), where r is the distance from the center of the sphere and e is a constant.
Gradient Vector:
The gradient vector of a scalar function represents the direction of the steepest increase of the function. In this case, the scalar function is the electric potential.
Direction of the Gradient Vector:
To determine the direction of the gradient vector, we need to consider the charge distribution and the electric potential.
Radial Inward Direction:
If the gradient vector points radially inwards, it would imply that the electric potential decreases as we move away from the center of the sphere. However, in the case of a charged sphere, the electric potential increases as we move away from the center. Therefore, the gradient vector cannot point radially inwards.
Radial Outward Direction:
Since the electric potential increases as we move away from the center of the sphere, the gradient vector must point radially outward. This is because the direction of the steepest increase in the potential is away from the center of the sphere.
Tangential Direction:
The gradient vector does not point tangentially in any direction. It represents the direction of the steepest increase of the potential, which is always radial.
Clockwise or Anti-clockwise Direction:
The gradient vector does not have a rotational component, so it does not have a specific clockwise or anti-clockwise direction.
Therefore, the correct answer is option 'B' - the gradient vector to the family of equipotential surfaces of this charged sphere points radially outward.
Equipotential surfaces are surfaces in a region where the potential is constant. In the case of a charged sphere, the equipotential surfaces are spherical shells concentric with the sphere.
Charge Density:
The charge density of the sphere is given by f(r) = e^(-r), where r is the distance from the center of the sphere and e is a constant.
Gradient Vector:
The gradient vector of a scalar function represents the direction of the steepest increase of the function. In this case, the scalar function is the electric potential.
Direction of the Gradient Vector:
To determine the direction of the gradient vector, we need to consider the charge distribution and the electric potential.
Radial Inward Direction:
If the gradient vector points radially inwards, it would imply that the electric potential decreases as we move away from the center of the sphere. However, in the case of a charged sphere, the electric potential increases as we move away from the center. Therefore, the gradient vector cannot point radially inwards.
Radial Outward Direction:
Since the electric potential increases as we move away from the center of the sphere, the gradient vector must point radially outward. This is because the direction of the steepest increase in the potential is away from the center of the sphere.
Tangential Direction:
The gradient vector does not point tangentially in any direction. It represents the direction of the steepest increase of the potential, which is always radial.
Clockwise or Anti-clockwise Direction:
The gradient vector does not have a rotational component, so it does not have a specific clockwise or anti-clockwise direction.
Therefore, the correct answer is option 'B' - the gradient vector to the family of equipotential surfaces of this charged sphere points radially outward.
|
Explore Courses for GATE exam
|
|
Consider a charged sphere of radius R with charge density f(r ) = e-r. The gradient vector to the family of equipotential surfaces of this charged surface pointsa)radially inwardsb)radially outwardsc)tangentially in the clockwise directiond)tangentially in the anti-clockwise directionCorrect answer is option 'B'. Can you explain this answer?
Question Description
Consider a charged sphere of radius R with charge density f(r ) = e-r. The gradient vector to the family of equipotential surfaces of this charged surface pointsa)radially inwardsb)radially outwardsc)tangentially in the clockwise directiond)tangentially in the anti-clockwise directionCorrect answer is option 'B'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about Consider a charged sphere of radius R with charge density f(r ) = e-r. The gradient vector to the family of equipotential surfaces of this charged surface pointsa)radially inwardsb)radially outwardsc)tangentially in the clockwise directiond)tangentially in the anti-clockwise directionCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider a charged sphere of radius R with charge density f(r ) = e-r. The gradient vector to the family of equipotential surfaces of this charged surface pointsa)radially inwardsb)radially outwardsc)tangentially in the clockwise directiond)tangentially in the anti-clockwise directionCorrect answer is option 'B'. Can you explain this answer?.
Consider a charged sphere of radius R with charge density f(r ) = e-r. The gradient vector to the family of equipotential surfaces of this charged surface pointsa)radially inwardsb)radially outwardsc)tangentially in the clockwise directiond)tangentially in the anti-clockwise directionCorrect answer is option 'B'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about Consider a charged sphere of radius R with charge density f(r ) = e-r. The gradient vector to the family of equipotential surfaces of this charged surface pointsa)radially inwardsb)radially outwardsc)tangentially in the clockwise directiond)tangentially in the anti-clockwise directionCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider a charged sphere of radius R with charge density f(r ) = e-r. The gradient vector to the family of equipotential surfaces of this charged surface pointsa)radially inwardsb)radially outwardsc)tangentially in the clockwise directiond)tangentially in the anti-clockwise directionCorrect answer is option 'B'. Can you explain this answer?.
Solutions for Consider a charged sphere of radius R with charge density f(r ) = e-r. The gradient vector to the family of equipotential surfaces of this charged surface pointsa)radially inwardsb)radially outwardsc)tangentially in the clockwise directiond)tangentially in the anti-clockwise directionCorrect answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for GATE.
Download more important topics, notes, lectures and mock test series for GATE Exam by signing up for free.
Here you can find the meaning of Consider a charged sphere of radius R with charge density f(r ) = e-r. The gradient vector to the family of equipotential surfaces of this charged surface pointsa)radially inwardsb)radially outwardsc)tangentially in the clockwise directiond)tangentially in the anti-clockwise directionCorrect answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Consider a charged sphere of radius R with charge density f(r ) = e-r. The gradient vector to the family of equipotential surfaces of this charged surface pointsa)radially inwardsb)radially outwardsc)tangentially in the clockwise directiond)tangentially in the anti-clockwise directionCorrect answer is option 'B'. Can you explain this answer?, a detailed solution for Consider a charged sphere of radius R with charge density f(r ) = e-r. The gradient vector to the family of equipotential surfaces of this charged surface pointsa)radially inwardsb)radially outwardsc)tangentially in the clockwise directiond)tangentially in the anti-clockwise directionCorrect answer is option 'B'. Can you explain this answer? has been provided alongside types of Consider a charged sphere of radius R with charge density f(r ) = e-r. The gradient vector to the family of equipotential surfaces of this charged surface pointsa)radially inwardsb)radially outwardsc)tangentially in the clockwise directiond)tangentially in the anti-clockwise directionCorrect answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Consider a charged sphere of radius R with charge density f(r ) = e-r. The gradient vector to the family of equipotential surfaces of this charged surface pointsa)radially inwardsb)radially outwardsc)tangentially in the clockwise directiond)tangentially in the anti-clockwise directionCorrect answer is option 'B'. Can you explain this answer? tests, examples and also practice GATE tests.
|
|
Explore Courses for GATE exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup