GATE Exam > GATE Questions > Which of the following statements is/are FALS...
Start Learning for Free
Which of the following statements is/are FALSE?
(1) For every non-deterministic Turing machine, there exists an equivalent deterministic
Turing machine.
(2) Turing recognizable languages are closed under union and complementation.
(3) Turing decidable languages are closed under intersection and complementation
(4) Turing recognizable languages are closed under union and intersection.
(1) For every non-deterministic Turing machine, there exists an equivalent deterministic
Turing machine.
(2) Turing recognizable languages are closed under union and complementation.
(3) Turing decidable languages are closed under intersection and complementation
(4) Turing recognizable languages are closed under union and intersection.
- a)1 and 4 only
- b)1 and 3 only
- c)2 only
- d)3 only
Correct answer is option 'C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Which of the following statements is/are FALSE?(1) For every non-deter...
(1) NTM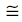 
DTM
(2) RELs are closed under union & but not complementation
(3) Turing decidable languages are recursive and recursive languages are closed under
intersection and complementation
(4) RELs are closed under union & intersection but not under complementation
DTM(2) RELs are closed under union & but not complementation
(3) Turing decidable languages are recursive and recursive languages are closed under
intersection and complementation
(4) RELs are closed under union & intersection but not under complementation
Most Upvoted Answer
Which of the following statements is/are FALSE?(1) For every non-deter...
False Statements:
1) For every non-deterministic Turing machine, there exists an equivalent deterministic Turing machine.
3) Turing decidable languages are closed under intersection and complementation.
Explanation:
1) For every non-deterministic Turing machine, there exists an equivalent deterministic Turing machine.
This statement is false. Non-deterministic Turing machines (NTMs) have the ability to transition to multiple states simultaneously, while deterministic Turing machines (DTMs) can only transition to a single state. Therefore, the behavior of an NTM cannot always be simulated by a DTM. There are cases where an NTM can solve a problem in polynomial time, while the corresponding DTM would require exponential time. Thus, NTMs are more powerful than DTMs in terms of time complexity. Hence, there does not exist an equivalent deterministic Turing machine for every non-deterministic Turing machine.
3) Turing decidable languages are closed under intersection and complementation.
This statement is false. A language L is said to be Turing decidable if there exists a Turing machine that halts and accepts any string in L, and halts and rejects any string not in L. It is known that Turing decidable languages are closed under complementation, i.e., if L is Turing decidable, then its complement L' is also Turing decidable. However, Turing decidable languages are not closed under intersection. That is, given two Turing decidable languages L1 and L2, it is not always possible to construct a Turing machine that can decide whether a given string belongs to the intersection of L1 and L2. This is because the Turing machine would have to simulate both L1 and L2 simultaneously, which may not be feasible in all cases. Therefore, Turing decidable languages are not closed under intersection.
Hence, the false statements are 1) For every non-deterministic Turing machine, there exists an equivalent deterministic Turing machine, and 3) Turing decidable languages are closed under intersection and complementation. Therefore, the correct answer is option C) 2 only.
1) For every non-deterministic Turing machine, there exists an equivalent deterministic Turing machine.
3) Turing decidable languages are closed under intersection and complementation.
Explanation:
1) For every non-deterministic Turing machine, there exists an equivalent deterministic Turing machine.
This statement is false. Non-deterministic Turing machines (NTMs) have the ability to transition to multiple states simultaneously, while deterministic Turing machines (DTMs) can only transition to a single state. Therefore, the behavior of an NTM cannot always be simulated by a DTM. There are cases where an NTM can solve a problem in polynomial time, while the corresponding DTM would require exponential time. Thus, NTMs are more powerful than DTMs in terms of time complexity. Hence, there does not exist an equivalent deterministic Turing machine for every non-deterministic Turing machine.
3) Turing decidable languages are closed under intersection and complementation.
This statement is false. A language L is said to be Turing decidable if there exists a Turing machine that halts and accepts any string in L, and halts and rejects any string not in L. It is known that Turing decidable languages are closed under complementation, i.e., if L is Turing decidable, then its complement L' is also Turing decidable. However, Turing decidable languages are not closed under intersection. That is, given two Turing decidable languages L1 and L2, it is not always possible to construct a Turing machine that can decide whether a given string belongs to the intersection of L1 and L2. This is because the Turing machine would have to simulate both L1 and L2 simultaneously, which may not be feasible in all cases. Therefore, Turing decidable languages are not closed under intersection.
Hence, the false statements are 1) For every non-deterministic Turing machine, there exists an equivalent deterministic Turing machine, and 3) Turing decidable languages are closed under intersection and complementation. Therefore, the correct answer is option C) 2 only.
|
Explore Courses for GATE exam
|
|
Similar GATE Doubts
Which of the following statements is/are FALSE?(1) For every non-deterministic Turing machine, there exists an equivalent deterministicTuring machine.(2) Turing recognizable languages are closed under union and complementation.(3) Turing decidable languages are closed under intersection and complementation(4) Turing recognizable languages are closed under union and intersection.a)1 and 4 onlyb)1 and 3 onlyc)2 onlyd)3 onlyCorrect answer is option 'C'. Can you explain this answer?
Question Description
Which of the following statements is/are FALSE?(1) For every non-deterministic Turing machine, there exists an equivalent deterministicTuring machine.(2) Turing recognizable languages are closed under union and complementation.(3) Turing decidable languages are closed under intersection and complementation(4) Turing recognizable languages are closed under union and intersection.a)1 and 4 onlyb)1 and 3 onlyc)2 onlyd)3 onlyCorrect answer is option 'C'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about Which of the following statements is/are FALSE?(1) For every non-deterministic Turing machine, there exists an equivalent deterministicTuring machine.(2) Turing recognizable languages are closed under union and complementation.(3) Turing decidable languages are closed under intersection and complementation(4) Turing recognizable languages are closed under union and intersection.a)1 and 4 onlyb)1 and 3 onlyc)2 onlyd)3 onlyCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Which of the following statements is/are FALSE?(1) For every non-deterministic Turing machine, there exists an equivalent deterministicTuring machine.(2) Turing recognizable languages are closed under union and complementation.(3) Turing decidable languages are closed under intersection and complementation(4) Turing recognizable languages are closed under union and intersection.a)1 and 4 onlyb)1 and 3 onlyc)2 onlyd)3 onlyCorrect answer is option 'C'. Can you explain this answer?.
Which of the following statements is/are FALSE?(1) For every non-deterministic Turing machine, there exists an equivalent deterministicTuring machine.(2) Turing recognizable languages are closed under union and complementation.(3) Turing decidable languages are closed under intersection and complementation(4) Turing recognizable languages are closed under union and intersection.a)1 and 4 onlyb)1 and 3 onlyc)2 onlyd)3 onlyCorrect answer is option 'C'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about Which of the following statements is/are FALSE?(1) For every non-deterministic Turing machine, there exists an equivalent deterministicTuring machine.(2) Turing recognizable languages are closed under union and complementation.(3) Turing decidable languages are closed under intersection and complementation(4) Turing recognizable languages are closed under union and intersection.a)1 and 4 onlyb)1 and 3 onlyc)2 onlyd)3 onlyCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Which of the following statements is/are FALSE?(1) For every non-deterministic Turing machine, there exists an equivalent deterministicTuring machine.(2) Turing recognizable languages are closed under union and complementation.(3) Turing decidable languages are closed under intersection and complementation(4) Turing recognizable languages are closed under union and intersection.a)1 and 4 onlyb)1 and 3 onlyc)2 onlyd)3 onlyCorrect answer is option 'C'. Can you explain this answer?.
Solutions for Which of the following statements is/are FALSE?(1) For every non-deterministic Turing machine, there exists an equivalent deterministicTuring machine.(2) Turing recognizable languages are closed under union and complementation.(3) Turing decidable languages are closed under intersection and complementation(4) Turing recognizable languages are closed under union and intersection.a)1 and 4 onlyb)1 and 3 onlyc)2 onlyd)3 onlyCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for GATE.
Download more important topics, notes, lectures and mock test series for GATE Exam by signing up for free.
Here you can find the meaning of Which of the following statements is/are FALSE?(1) For every non-deterministic Turing machine, there exists an equivalent deterministicTuring machine.(2) Turing recognizable languages are closed under union and complementation.(3) Turing decidable languages are closed under intersection and complementation(4) Turing recognizable languages are closed under union and intersection.a)1 and 4 onlyb)1 and 3 onlyc)2 onlyd)3 onlyCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Which of the following statements is/are FALSE?(1) For every non-deterministic Turing machine, there exists an equivalent deterministicTuring machine.(2) Turing recognizable languages are closed under union and complementation.(3) Turing decidable languages are closed under intersection and complementation(4) Turing recognizable languages are closed under union and intersection.a)1 and 4 onlyb)1 and 3 onlyc)2 onlyd)3 onlyCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for Which of the following statements is/are FALSE?(1) For every non-deterministic Turing machine, there exists an equivalent deterministicTuring machine.(2) Turing recognizable languages are closed under union and complementation.(3) Turing decidable languages are closed under intersection and complementation(4) Turing recognizable languages are closed under union and intersection.a)1 and 4 onlyb)1 and 3 onlyc)2 onlyd)3 onlyCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of Which of the following statements is/are FALSE?(1) For every non-deterministic Turing machine, there exists an equivalent deterministicTuring machine.(2) Turing recognizable languages are closed under union and complementation.(3) Turing decidable languages are closed under intersection and complementation(4) Turing recognizable languages are closed under union and intersection.a)1 and 4 onlyb)1 and 3 onlyc)2 onlyd)3 onlyCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Which of the following statements is/are FALSE?(1) For every non-deterministic Turing machine, there exists an equivalent deterministicTuring machine.(2) Turing recognizable languages are closed under union and complementation.(3) Turing decidable languages are closed under intersection and complementation(4) Turing recognizable languages are closed under union and intersection.a)1 and 4 onlyb)1 and 3 onlyc)2 onlyd)3 onlyCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice GATE tests.
|
|
Explore Courses for GATE exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup