GATE Exam > GATE Questions > Consider a virtual system with 2 level paging...
Start Learning for Free
Consider a virtual system with 2 level paging 32 bit virtual address is used to support 32 bit physical address, Page size is 4096 byte pages and page table has 4 bytes of page table entry. How many memory accesses required to read or write a single word.
- a)4
- b)3
- c)2
- d)1
Correct answer is option 'B'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Consider a virtual system with 2 level paging 32 bit virtual address i...
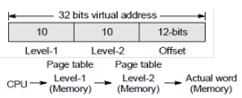
∴ 3 memory accesses are required.
Most Upvoted Answer
Consider a virtual system with 2 level paging 32 bit virtual address i...
Virtual System with 2 Level Paging
In a virtual system with 2 level paging, the virtual address is divided into multiple levels of page indexes. Each level corresponds to a page table, and the combination of all the page indexes forms the physical address.
In this scenario, we have a 32-bit virtual address and a 32-bit physical address. The page size is 4096 bytes (4KB), and each page table entry is 4 bytes.
Calculating the Number of Memory Accesses
To read or write a single word, we need to determine the number of memory accesses required. Let's break down the process step by step:
1. First Level Access: The virtual address is divided into two parts - the first-level index and the second-level index. Since we have a 32-bit virtual address, the first-level index corresponds to the upper 20 bits, and the second-level index corresponds to the lower 12 bits.
2. First Level Page Table Access: We need to access the first-level page table using the first-level index. Since each page table entry is 4 bytes, we divide the first-level index (20 bits) by 4 to get the number of entries in the first-level page table. In this case, it is 2^20 / 2^2 = 2^18 entries. Therefore, we need one memory access to read or write the first-level page table entry.
3. Second Level Access: Once we have obtained the first-level page table entry, we can use it to access the second-level page table. The second-level page index is obtained from the first-level page table entry. Since the second-level index corresponds to the lower 12 bits, we can directly use it to access the second-level page table.
4. Second Level Page Table Access: Similar to the first level, we divide the second-level index (12 bits) by 4 to get the number of entries in the second-level page table. In this case, it is 2^12 / 2^2 = 2^10 entries. Therefore, we need one memory access to read or write the second-level page table entry.
5. Page Offset Access: Once we have obtained the second-level page table entry, we can use it to determine the physical address. The page offset is obtained from the lower 12 bits of the virtual address, and it remains unchanged in the physical address. Therefore, no additional memory access is required to access the page offset.
Total Memory Accesses:
From the above analysis, we can see that we need two memory accesses - one to access the first-level page table and another to access the second-level page table. Therefore, the correct answer is option 'B' - 3 memory accesses are required to read or write a single word.
In a virtual system with 2 level paging, the virtual address is divided into multiple levels of page indexes. Each level corresponds to a page table, and the combination of all the page indexes forms the physical address.
In this scenario, we have a 32-bit virtual address and a 32-bit physical address. The page size is 4096 bytes (4KB), and each page table entry is 4 bytes.
Calculating the Number of Memory Accesses
To read or write a single word, we need to determine the number of memory accesses required. Let's break down the process step by step:
1. First Level Access: The virtual address is divided into two parts - the first-level index and the second-level index. Since we have a 32-bit virtual address, the first-level index corresponds to the upper 20 bits, and the second-level index corresponds to the lower 12 bits.
2. First Level Page Table Access: We need to access the first-level page table using the first-level index. Since each page table entry is 4 bytes, we divide the first-level index (20 bits) by 4 to get the number of entries in the first-level page table. In this case, it is 2^20 / 2^2 = 2^18 entries. Therefore, we need one memory access to read or write the first-level page table entry.
3. Second Level Access: Once we have obtained the first-level page table entry, we can use it to access the second-level page table. The second-level page index is obtained from the first-level page table entry. Since the second-level index corresponds to the lower 12 bits, we can directly use it to access the second-level page table.
4. Second Level Page Table Access: Similar to the first level, we divide the second-level index (12 bits) by 4 to get the number of entries in the second-level page table. In this case, it is 2^12 / 2^2 = 2^10 entries. Therefore, we need one memory access to read or write the second-level page table entry.
5. Page Offset Access: Once we have obtained the second-level page table entry, we can use it to determine the physical address. The page offset is obtained from the lower 12 bits of the virtual address, and it remains unchanged in the physical address. Therefore, no additional memory access is required to access the page offset.
Total Memory Accesses:
From the above analysis, we can see that we need two memory accesses - one to access the first-level page table and another to access the second-level page table. Therefore, the correct answer is option 'B' - 3 memory accesses are required to read or write a single word.

|
Explore Courses for GATE exam
|

|
Similar GATE Doubts
Consider a virtual system with 2 level paging 32 bit virtual address is used to support 32 bit physical address, Page size is 4096 byte pages and page table has 4 bytes of page table entry. How many memory accesses required to read or write a single word.a)4b)3c)2d)1Correct answer is option 'B'. Can you explain this answer?
Question Description
Consider a virtual system with 2 level paging 32 bit virtual address is used to support 32 bit physical address, Page size is 4096 byte pages and page table has 4 bytes of page table entry. How many memory accesses required to read or write a single word.a)4b)3c)2d)1Correct answer is option 'B'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about Consider a virtual system with 2 level paging 32 bit virtual address is used to support 32 bit physical address, Page size is 4096 byte pages and page table has 4 bytes of page table entry. How many memory accesses required to read or write a single word.a)4b)3c)2d)1Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider a virtual system with 2 level paging 32 bit virtual address is used to support 32 bit physical address, Page size is 4096 byte pages and page table has 4 bytes of page table entry. How many memory accesses required to read or write a single word.a)4b)3c)2d)1Correct answer is option 'B'. Can you explain this answer?.
Consider a virtual system with 2 level paging 32 bit virtual address is used to support 32 bit physical address, Page size is 4096 byte pages and page table has 4 bytes of page table entry. How many memory accesses required to read or write a single word.a)4b)3c)2d)1Correct answer is option 'B'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about Consider a virtual system with 2 level paging 32 bit virtual address is used to support 32 bit physical address, Page size is 4096 byte pages and page table has 4 bytes of page table entry. How many memory accesses required to read or write a single word.a)4b)3c)2d)1Correct answer is option 'B'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Consider a virtual system with 2 level paging 32 bit virtual address is used to support 32 bit physical address, Page size is 4096 byte pages and page table has 4 bytes of page table entry. How many memory accesses required to read or write a single word.a)4b)3c)2d)1Correct answer is option 'B'. Can you explain this answer?.
Solutions for Consider a virtual system with 2 level paging 32 bit virtual address is used to support 32 bit physical address, Page size is 4096 byte pages and page table has 4 bytes of page table entry. How many memory accesses required to read or write a single word.a)4b)3c)2d)1Correct answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for GATE.
Download more important topics, notes, lectures and mock test series for GATE Exam by signing up for free.
Here you can find the meaning of Consider a virtual system with 2 level paging 32 bit virtual address is used to support 32 bit physical address, Page size is 4096 byte pages and page table has 4 bytes of page table entry. How many memory accesses required to read or write a single word.a)4b)3c)2d)1Correct answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Consider a virtual system with 2 level paging 32 bit virtual address is used to support 32 bit physical address, Page size is 4096 byte pages and page table has 4 bytes of page table entry. How many memory accesses required to read or write a single word.a)4b)3c)2d)1Correct answer is option 'B'. Can you explain this answer?, a detailed solution for Consider a virtual system with 2 level paging 32 bit virtual address is used to support 32 bit physical address, Page size is 4096 byte pages and page table has 4 bytes of page table entry. How many memory accesses required to read or write a single word.a)4b)3c)2d)1Correct answer is option 'B'. Can you explain this answer? has been provided alongside types of Consider a virtual system with 2 level paging 32 bit virtual address is used to support 32 bit physical address, Page size is 4096 byte pages and page table has 4 bytes of page table entry. How many memory accesses required to read or write a single word.a)4b)3c)2d)1Correct answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Consider a virtual system with 2 level paging 32 bit virtual address is used to support 32 bit physical address, Page size is 4096 byte pages and page table has 4 bytes of page table entry. How many memory accesses required to read or write a single word.a)4b)3c)2d)1Correct answer is option 'B'. Can you explain this answer? tests, examples and also practice GATE tests.

|
Explore Courses for GATE exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















