GATE Exam > GATE Questions > The entropy of a system, S, is related to the...
Start Learning for Free
The entropy of a system, S, is related to the accessible phase space volume G by S = kBlnG(E, N, V) where E, N and V are the energy, number of particles and volume respectively. From this one can conclude that G
- a)does not change during evolution to equilibrium
- b)oscillates during evolution to equilibrium
- c)is a maximum at equilibrium
- d)is a minimum at equilibrium
Correct answer is option 'C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
The entropy of a system, S, is related to the accessible phase space v...
Two macroscopic system, which are in thermal contact, the required condition for the equilibrium is that their b parameter must be equal.
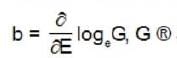accessible phase space volume
So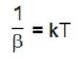
on comparing
S = klnr(E,V,N)
and it is obvious that at equilibrium the accessible phase volume is maximum.
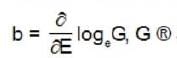accessible phase space volume So
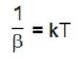
on comparing
S = klnr(E,V,N)
and it is obvious that at equilibrium the accessible phase volume is maximum.
Most Upvoted Answer
The entropy of a system, S, is related to the accessible phase space v...
Explanation:
The entropy of a system, denoted by S, is a measure of the number of microscopic arrangements or configurations corresponding to a given macroscopic state. It quantifies the level of disorder or randomness in the system. The greater the number of configurations, the higher the entropy.
The accessible phase space volume, denoted by G, represents the volume in the phase space that is accessible to the system given its energy, number of particles, and volume.
The relationship between entropy and accessible phase space volume is given by the equation S = k * ln(G), where k is the Boltzmann constant. This equation is derived from statistical mechanics.
At equilibrium:
At equilibrium, the system has reached a state of maximum entropy. This means that the system has explored all possible configurations and has settled into the most probable state. In this state, the accessible phase space volume is maximized.
Options:
The correct answer is option C, which states that the accessible phase space volume is a maximum at equilibrium. This is consistent with the understanding that equilibrium corresponds to the state of maximum entropy.
Option A, which states that the accessible phase space volume does not change during evolution to equilibrium, is incorrect. The system evolves towards equilibrium by exploring different configurations, and the accessible phase space volume changes as the system explores new states.
Option B, which states that the accessible phase space volume oscillates during evolution to equilibrium, is incorrect. The evolution towards equilibrium is a gradual process of exploration and settling into the most probable state, rather than oscillations.
Option D, which states that the accessible phase space volume is a minimum at equilibrium, is incorrect. The system reaches a state of maximum entropy at equilibrium, which corresponds to a maximum accessible phase space volume.
In conclusion, the accessible phase space volume is a maximum at equilibrium, which corresponds to the state of maximum entropy.
The entropy of a system, denoted by S, is a measure of the number of microscopic arrangements or configurations corresponding to a given macroscopic state. It quantifies the level of disorder or randomness in the system. The greater the number of configurations, the higher the entropy.
The accessible phase space volume, denoted by G, represents the volume in the phase space that is accessible to the system given its energy, number of particles, and volume.
The relationship between entropy and accessible phase space volume is given by the equation S = k * ln(G), where k is the Boltzmann constant. This equation is derived from statistical mechanics.
At equilibrium:
At equilibrium, the system has reached a state of maximum entropy. This means that the system has explored all possible configurations and has settled into the most probable state. In this state, the accessible phase space volume is maximized.
Options:
The correct answer is option C, which states that the accessible phase space volume is a maximum at equilibrium. This is consistent with the understanding that equilibrium corresponds to the state of maximum entropy.
Option A, which states that the accessible phase space volume does not change during evolution to equilibrium, is incorrect. The system evolves towards equilibrium by exploring different configurations, and the accessible phase space volume changes as the system explores new states.
Option B, which states that the accessible phase space volume oscillates during evolution to equilibrium, is incorrect. The evolution towards equilibrium is a gradual process of exploration and settling into the most probable state, rather than oscillations.
Option D, which states that the accessible phase space volume is a minimum at equilibrium, is incorrect. The system reaches a state of maximum entropy at equilibrium, which corresponds to a maximum accessible phase space volume.
In conclusion, the accessible phase space volume is a maximum at equilibrium, which corresponds to the state of maximum entropy.
|
Explore Courses for GATE exam
|
|
Similar GATE Doubts
The entropy of a system, S, is related to the accessible phase space volume G by S = kBlnG(E, N, V) where E, N and V are the energy, number of particles and volume respectively. From this one can conclude that Ga)does not change during evolution to equilibriumb)oscillates during evolution to equilibriumc)is a maximum at equilibriumd)is a minimum at equilibriumCorrect answer is option 'C'. Can you explain this answer?
Question Description
The entropy of a system, S, is related to the accessible phase space volume G by S = kBlnG(E, N, V) where E, N and V are the energy, number of particles and volume respectively. From this one can conclude that Ga)does not change during evolution to equilibriumb)oscillates during evolution to equilibriumc)is a maximum at equilibriumd)is a minimum at equilibriumCorrect answer is option 'C'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about The entropy of a system, S, is related to the accessible phase space volume G by S = kBlnG(E, N, V) where E, N and V are the energy, number of particles and volume respectively. From this one can conclude that Ga)does not change during evolution to equilibriumb)oscillates during evolution to equilibriumc)is a maximum at equilibriumd)is a minimum at equilibriumCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The entropy of a system, S, is related to the accessible phase space volume G by S = kBlnG(E, N, V) where E, N and V are the energy, number of particles and volume respectively. From this one can conclude that Ga)does not change during evolution to equilibriumb)oscillates during evolution to equilibriumc)is a maximum at equilibriumd)is a minimum at equilibriumCorrect answer is option 'C'. Can you explain this answer?.
The entropy of a system, S, is related to the accessible phase space volume G by S = kBlnG(E, N, V) where E, N and V are the energy, number of particles and volume respectively. From this one can conclude that Ga)does not change during evolution to equilibriumb)oscillates during evolution to equilibriumc)is a maximum at equilibriumd)is a minimum at equilibriumCorrect answer is option 'C'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about The entropy of a system, S, is related to the accessible phase space volume G by S = kBlnG(E, N, V) where E, N and V are the energy, number of particles and volume respectively. From this one can conclude that Ga)does not change during evolution to equilibriumb)oscillates during evolution to equilibriumc)is a maximum at equilibriumd)is a minimum at equilibriumCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The entropy of a system, S, is related to the accessible phase space volume G by S = kBlnG(E, N, V) where E, N and V are the energy, number of particles and volume respectively. From this one can conclude that Ga)does not change during evolution to equilibriumb)oscillates during evolution to equilibriumc)is a maximum at equilibriumd)is a minimum at equilibriumCorrect answer is option 'C'. Can you explain this answer?.
Solutions for The entropy of a system, S, is related to the accessible phase space volume G by S = kBlnG(E, N, V) where E, N and V are the energy, number of particles and volume respectively. From this one can conclude that Ga)does not change during evolution to equilibriumb)oscillates during evolution to equilibriumc)is a maximum at equilibriumd)is a minimum at equilibriumCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for GATE.
Download more important topics, notes, lectures and mock test series for GATE Exam by signing up for free.
Here you can find the meaning of The entropy of a system, S, is related to the accessible phase space volume G by S = kBlnG(E, N, V) where E, N and V are the energy, number of particles and volume respectively. From this one can conclude that Ga)does not change during evolution to equilibriumb)oscillates during evolution to equilibriumc)is a maximum at equilibriumd)is a minimum at equilibriumCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The entropy of a system, S, is related to the accessible phase space volume G by S = kBlnG(E, N, V) where E, N and V are the energy, number of particles and volume respectively. From this one can conclude that Ga)does not change during evolution to equilibriumb)oscillates during evolution to equilibriumc)is a maximum at equilibriumd)is a minimum at equilibriumCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for The entropy of a system, S, is related to the accessible phase space volume G by S = kBlnG(E, N, V) where E, N and V are the energy, number of particles and volume respectively. From this one can conclude that Ga)does not change during evolution to equilibriumb)oscillates during evolution to equilibriumc)is a maximum at equilibriumd)is a minimum at equilibriumCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of The entropy of a system, S, is related to the accessible phase space volume G by S = kBlnG(E, N, V) where E, N and V are the energy, number of particles and volume respectively. From this one can conclude that Ga)does not change during evolution to equilibriumb)oscillates during evolution to equilibriumc)is a maximum at equilibriumd)is a minimum at equilibriumCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The entropy of a system, S, is related to the accessible phase space volume G by S = kBlnG(E, N, V) where E, N and V are the energy, number of particles and volume respectively. From this one can conclude that Ga)does not change during evolution to equilibriumb)oscillates during evolution to equilibriumc)is a maximum at equilibriumd)is a minimum at equilibriumCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice GATE tests.
|
|
Explore Courses for GATE exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup