GATE Exam > GATE Questions > A planet is revolving around a star in an ell...
Start Learning for Free
A planet is revolving around a star in an elliptic orbit. The ratio of the farthest distance to the closest distance of the planet from the star is 4. The ratio of kinetic energies of the planet at the closest to farthest position is ______ .
Correct answer is '16'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A planet is revolving around a star in an elliptic orbit. The ratio of...
Angular momentum is conserved during revolution of planet, because gravitational force is a central force,
m r1 v1 = m r2v2
or since L is constant hence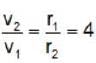
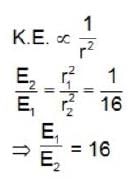
m r1 v1 = m r2v2
or since L is constant hence
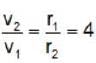
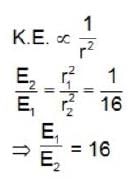
Most Upvoted Answer
A planet is revolving around a star in an elliptic orbit. The ratio of...
Explanation:
Given:
- A planet is revolving around a star in an elliptic orbit.
- The ratio of the farthest distance to the closest distance of the planet from the star is 4.
Kepler's Second Law:
Kepler's Second Law states that the line joining a planet to the star sweeps out equal areas in equal times. This means that the speed of the planet is not constant throughout its orbit. As the planet gets closer to the star, it moves faster, and as it gets farther away, it slows down.
Kinetic Energy:
The kinetic energy of an object is given by the formula KE = 1/2 * m * v^2, where m is the mass of the object and v is its velocity.
Analysis:
1. Let's assume that the closest distance of the planet from the star is d.
2. According to the given information, the farthest distance of the planet from the star is 4d.
3. As the planet moves from the closest distance to the farthest distance, its speed decreases.
4. Since kinetic energy is directly proportional to the square of velocity, the kinetic energy of the planet at the farthest distance will be less than its kinetic energy at the closest distance.
Calculating the Ratio of Kinetic Energies:
1. Let's assume the mass of the planet remains constant throughout its orbit.
2. At the closest distance, let's assume the velocity of the planet is v1. Therefore, the kinetic energy at the closest distance is KE1 = 1/2 * m * v1^2.
3. At the farthest distance, let's assume the velocity of the planet is v2. Therefore, the kinetic energy at the farthest distance is KE2 = 1/2 * m * v2^2.
4. According to Kepler's Second Law, the planet sweeps out equal areas in equal times. This means that the time taken by the planet to cover the closest distance is equal to the time taken to cover the farthest distance.
5. Since the mass of the planet remains constant, we can write v1 * t1 = v2 * t2, where t1 and t2 are the times taken to cover the closest and farthest distances, respectively.
6. Since the time taken is the same, we can write v1/v2 = t2/t1.
7. As the planet gets farther away, it slows down, so v2 < />
8. Therefore, t2/t1 < />
9. Since v1/v2 = t2/t1, we can say that v1/v2 < />
10. Since the kinetic energy is directly proportional to the square of velocity, (v1/v2)^2 < />
11. Therefore, KE1/KE2 = (v1^2)/(v2^2) < />
12. We know that the ratio of the farthest distance to the closest distance is 4. Therefore, v1/v2 = 4.
13. Substituting this value in the equation, (4^2) = KE1/KE2.
14. Simplifying, we get 16 = KE1/KE2.
Conclusion:
The ratio of the kinetic energies of the planet at the closest to farthest
Given:
- A planet is revolving around a star in an elliptic orbit.
- The ratio of the farthest distance to the closest distance of the planet from the star is 4.
Kepler's Second Law:
Kepler's Second Law states that the line joining a planet to the star sweeps out equal areas in equal times. This means that the speed of the planet is not constant throughout its orbit. As the planet gets closer to the star, it moves faster, and as it gets farther away, it slows down.
Kinetic Energy:
The kinetic energy of an object is given by the formula KE = 1/2 * m * v^2, where m is the mass of the object and v is its velocity.
Analysis:
1. Let's assume that the closest distance of the planet from the star is d.
2. According to the given information, the farthest distance of the planet from the star is 4d.
3. As the planet moves from the closest distance to the farthest distance, its speed decreases.
4. Since kinetic energy is directly proportional to the square of velocity, the kinetic energy of the planet at the farthest distance will be less than its kinetic energy at the closest distance.
Calculating the Ratio of Kinetic Energies:
1. Let's assume the mass of the planet remains constant throughout its orbit.
2. At the closest distance, let's assume the velocity of the planet is v1. Therefore, the kinetic energy at the closest distance is KE1 = 1/2 * m * v1^2.
3. At the farthest distance, let's assume the velocity of the planet is v2. Therefore, the kinetic energy at the farthest distance is KE2 = 1/2 * m * v2^2.
4. According to Kepler's Second Law, the planet sweeps out equal areas in equal times. This means that the time taken by the planet to cover the closest distance is equal to the time taken to cover the farthest distance.
5. Since the mass of the planet remains constant, we can write v1 * t1 = v2 * t2, where t1 and t2 are the times taken to cover the closest and farthest distances, respectively.
6. Since the time taken is the same, we can write v1/v2 = t2/t1.
7. As the planet gets farther away, it slows down, so v2 < />
8. Therefore, t2/t1 < />
9. Since v1/v2 = t2/t1, we can say that v1/v2 < />
10. Since the kinetic energy is directly proportional to the square of velocity, (v1/v2)^2 < />
11. Therefore, KE1/KE2 = (v1^2)/(v2^2) < />
12. We know that the ratio of the farthest distance to the closest distance is 4. Therefore, v1/v2 = 4.
13. Substituting this value in the equation, (4^2) = KE1/KE2.
14. Simplifying, we get 16 = KE1/KE2.
Conclusion:
The ratio of the kinetic energies of the planet at the closest to farthest

|
Explore Courses for GATE exam
|

|
Similar GATE Doubts
A planet is revolving around a star in an elliptic orbit. The ratio of the farthest distance to the closest distance of the planet from the star is 4. The ratio of kinetic energies of the planet at the closest to farthest position is ______ .Correct answer is '16'. Can you explain this answer?
Question Description
A planet is revolving around a star in an elliptic orbit. The ratio of the farthest distance to the closest distance of the planet from the star is 4. The ratio of kinetic energies of the planet at the closest to farthest position is ______ .Correct answer is '16'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about A planet is revolving around a star in an elliptic orbit. The ratio of the farthest distance to the closest distance of the planet from the star is 4. The ratio of kinetic energies of the planet at the closest to farthest position is ______ .Correct answer is '16'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A planet is revolving around a star in an elliptic orbit. The ratio of the farthest distance to the closest distance of the planet from the star is 4. The ratio of kinetic energies of the planet at the closest to farthest position is ______ .Correct answer is '16'. Can you explain this answer?.
A planet is revolving around a star in an elliptic orbit. The ratio of the farthest distance to the closest distance of the planet from the star is 4. The ratio of kinetic energies of the planet at the closest to farthest position is ______ .Correct answer is '16'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about A planet is revolving around a star in an elliptic orbit. The ratio of the farthest distance to the closest distance of the planet from the star is 4. The ratio of kinetic energies of the planet at the closest to farthest position is ______ .Correct answer is '16'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A planet is revolving around a star in an elliptic orbit. The ratio of the farthest distance to the closest distance of the planet from the star is 4. The ratio of kinetic energies of the planet at the closest to farthest position is ______ .Correct answer is '16'. Can you explain this answer?.
Solutions for A planet is revolving around a star in an elliptic orbit. The ratio of the farthest distance to the closest distance of the planet from the star is 4. The ratio of kinetic energies of the planet at the closest to farthest position is ______ .Correct answer is '16'. Can you explain this answer? in English & in Hindi are available as part of our courses for GATE.
Download more important topics, notes, lectures and mock test series for GATE Exam by signing up for free.
Here you can find the meaning of A planet is revolving around a star in an elliptic orbit. The ratio of the farthest distance to the closest distance of the planet from the star is 4. The ratio of kinetic energies of the planet at the closest to farthest position is ______ .Correct answer is '16'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A planet is revolving around a star in an elliptic orbit. The ratio of the farthest distance to the closest distance of the planet from the star is 4. The ratio of kinetic energies of the planet at the closest to farthest position is ______ .Correct answer is '16'. Can you explain this answer?, a detailed solution for A planet is revolving around a star in an elliptic orbit. The ratio of the farthest distance to the closest distance of the planet from the star is 4. The ratio of kinetic energies of the planet at the closest to farthest position is ______ .Correct answer is '16'. Can you explain this answer? has been provided alongside types of A planet is revolving around a star in an elliptic orbit. The ratio of the farthest distance to the closest distance of the planet from the star is 4. The ratio of kinetic energies of the planet at the closest to farthest position is ______ .Correct answer is '16'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A planet is revolving around a star in an elliptic orbit. The ratio of the farthest distance to the closest distance of the planet from the star is 4. The ratio of kinetic energies of the planet at the closest to farthest position is ______ .Correct answer is '16'. Can you explain this answer? tests, examples and also practice GATE tests.

|
Explore Courses for GATE exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















