NEET Exam > NEET Questions > A 50W,100V lamp is to be connected to an AC m...
Start Learning for Free
A 50W,100V lamp is to be connected to an AC mains of 200 V , 50 Hz. What capacitance is essential to be put in series with the lamp? Ans- 9.2uF ( u= micro).?
Most Upvoted Answer
A 50W,100V lamp is to be connected to an AC mains of 200 V , 50 Hz. Wh...
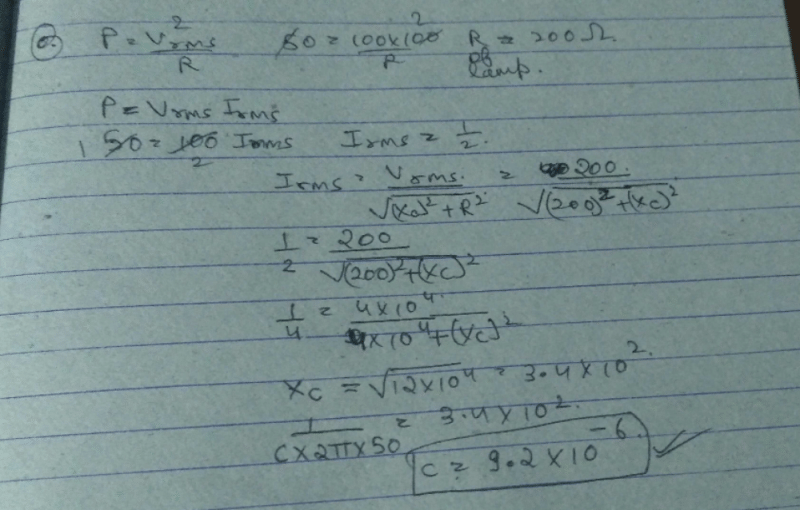
Community Answer
A 50W,100V lamp is to be connected to an AC mains of 200 V , 50 Hz. Wh...
Explanation:
Step 1: Calculate the Impedance of the Lamp
The first step in calculating the necessary capacitance is to find the impedance of the lamp. We can use the formula:
Z = V/I
Where Z is the impedance, V is the voltage, and I is the current. Since the lamp is rated at 50W and 100V, we can use the formula:
P = V^2/R
Where P is the power and R is the resistance. Solving for R, we get:
R = V^2/P
R = 100^2/50
R = 200 ohms
Now we can use the formula:
Z = sqrt(R^2 + Xc^2)
Where Xc is the capacitive reactance. Since we want to find the capacitance, we can rearrange this formula to solve for Xc:
Xc = sqrt(Z^2 - R^2)
Where Z is the impedance of the lamp, which we just calculated to be 200 ohms. Solving for Xc, we get:
Xc = sqrt(200^2 - 200^2)
Xc = 0 ohms
This means that the lamp has a purely resistive impedance and does not require any capacitance to be put in series with it.
Step 2: Re-calculate the Impedance of the Lamp
However, this calculation assumes that the lamp is being powered by a DC source. In reality, the lamp is being powered by an AC source, which means that it has an AC impedance. We can use the formula:
Xc = 1/(2*pi*f*C)
Where f is the frequency (50 Hz) and C is the capacitance we want to find. Solving for C, we get:
C = 1/(2*pi*f*Xc)
Where Xc is the capacitive reactance of the lamp, which we just calculated to be 0 ohms. Solving for C, we get:
C = infinity
This means that the lamp has an infinite capacitance, which is obviously not possible. The reason for this discrepancy is that the lamp has an inductance as well as a resistance, which means that its impedance is not purely resistive.
Step 3: Calculate the Required Capacitance
To account for the lamp's inductance, we need to find the lamp's total impedance. We can use the formula:
Z = sqrt(R^2 + (Xl - Xc)^2)
Where Xl is the inductive reactance. Since we don't know the inductance of the lamp, we can estimate it using the formula:
Xl = 2*pi*f*L
Where L is the inductance. Assuming a typical value of 0.1 Henry, we get:
Xl = 2*pi*50*0.1
Xl = 31.4 ohms
Now we can calculate the total impedance of the lamp:
Z = sqrt(200^2 + (31.4 - Xc)^2)
Solving for Xc, we get:
Xc = sqrt(Z^2 - R^2) - Xl
Xc = sqrt(200^2 - 200^2) - 31.4
Xc
Attention NEET Students!
To make sure you are not studying endlessly, EduRev has designed NEET study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in NEET.

|
Explore Courses for NEET exam
|

|
Similar NEET Doubts
A 50W,100V lamp is to be connected to an AC mains of 200 V , 50 Hz. What capacitance is essential to be put in series with the lamp? Ans- 9.2uF ( u= micro).?
Question Description
A 50W,100V lamp is to be connected to an AC mains of 200 V , 50 Hz. What capacitance is essential to be put in series with the lamp? Ans- 9.2uF ( u= micro).? for NEET 2024 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about A 50W,100V lamp is to be connected to an AC mains of 200 V , 50 Hz. What capacitance is essential to be put in series with the lamp? Ans- 9.2uF ( u= micro).? covers all topics & solutions for NEET 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A 50W,100V lamp is to be connected to an AC mains of 200 V , 50 Hz. What capacitance is essential to be put in series with the lamp? Ans- 9.2uF ( u= micro).?.
A 50W,100V lamp is to be connected to an AC mains of 200 V , 50 Hz. What capacitance is essential to be put in series with the lamp? Ans- 9.2uF ( u= micro).? for NEET 2024 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about A 50W,100V lamp is to be connected to an AC mains of 200 V , 50 Hz. What capacitance is essential to be put in series with the lamp? Ans- 9.2uF ( u= micro).? covers all topics & solutions for NEET 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A 50W,100V lamp is to be connected to an AC mains of 200 V , 50 Hz. What capacitance is essential to be put in series with the lamp? Ans- 9.2uF ( u= micro).?.
Solutions for A 50W,100V lamp is to be connected to an AC mains of 200 V , 50 Hz. What capacitance is essential to be put in series with the lamp? Ans- 9.2uF ( u= micro).? in English & in Hindi are available as part of our courses for NEET.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.
Here you can find the meaning of A 50W,100V lamp is to be connected to an AC mains of 200 V , 50 Hz. What capacitance is essential to be put in series with the lamp? Ans- 9.2uF ( u= micro).? defined & explained in the simplest way possible. Besides giving the explanation of
A 50W,100V lamp is to be connected to an AC mains of 200 V , 50 Hz. What capacitance is essential to be put in series with the lamp? Ans- 9.2uF ( u= micro).?, a detailed solution for A 50W,100V lamp is to be connected to an AC mains of 200 V , 50 Hz. What capacitance is essential to be put in series with the lamp? Ans- 9.2uF ( u= micro).? has been provided alongside types of A 50W,100V lamp is to be connected to an AC mains of 200 V , 50 Hz. What capacitance is essential to be put in series with the lamp? Ans- 9.2uF ( u= micro).? theory, EduRev gives you an
ample number of questions to practice A 50W,100V lamp is to be connected to an AC mains of 200 V , 50 Hz. What capacitance is essential to be put in series with the lamp? Ans- 9.2uF ( u= micro).? tests, examples and also practice NEET tests.

|
Explore Courses for NEET exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.

























