Physics Exam > Physics Questions > Calculate the pressure (in atmospheres) requi...
Start Learning for Free
Calculate the pressure (in atmospheres) required to make water freeze at - 10C. Change of specific volume when 1 gm of water freezes into ice = .091 cc.,J =4.2 x 107 ergs/cal..1 atmosphere 106 dynes / cm2 and the latent heat of ice = 80 cal./ gm.
Correct answer is '136.2'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Calculate the pressure (in atmospheres) required to make water freeze ...
Given dT = 10C . V2 - V1 = -0.091 c.c.
L = 80 cal. = 80 * 4.2 * 107 ergs, T = 0 + 273 = 273 K
Applying Clapeyrons latent heat equation
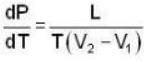
or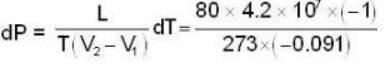
dynes/cm2.
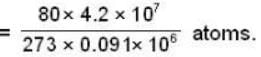
= 135.2 Atmos.
Hence to lower the melting of ice by 1°C, the pressure must be raised by 135.2 atmospheres.
Now melting point of ice at atmospheric pressure is 0°C. Hence pressure required to make ice freeze at - 1 °C
= 135.2 + 1 = 136.2 atmospheres
L = 80 cal. = 80 * 4.2 * 107 ergs, T = 0 + 273 = 273 K
Applying Clapeyrons latent heat equation
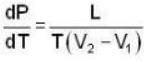
or
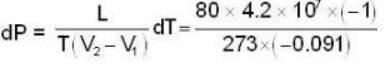dynes/cm2.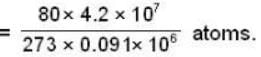= 135.2 Atmos.
Hence to lower the melting of ice by 1°C, the pressure must be raised by 135.2 atmospheres.
Now melting point of ice at atmospheric pressure is 0°C. Hence pressure required to make ice freeze at - 1 °C
= 135.2 + 1 = 136.2 atmospheres
Most Upvoted Answer
Calculate the pressure (in atmospheres) required to make water freeze ...
Given:
- Change in specific volume when 1 gm of water freezes into ice = 0.091 cc
- Latent heat of ice = 80 cal/gm
- J = 4.2 x 10^7 ergs/cal
- 1 atmosphere = 10^6 dynes/cm^2
To find:
Pressure required to make water freeze at -10°C in atmospheres
Solution:
Step 1: Convert the change in specific volume from cc to cm^3
Given change in specific volume = 0.091 cc
1 cc = 1 cm^3
Therefore, change in specific volume = 0.091 cm^3
Step 2: Convert the latent heat of ice from calories to ergs
Given latent heat of ice = 80 cal/gm
1 cal = 4.2 x 10^7 ergs
Therefore, latent heat of ice = 80 x 4.2 x 10^7 ergs
Step 3: Calculate the pressure required to make water freeze at -10°C
The change in specific volume when water freezes into ice is given by the equation:
ΔV = Vf - Vi
Where:
ΔV = change in specific volume
Vf = final specific volume of ice
Vi = initial specific volume of water
Given ΔV = 0.091 cm^3
Let's assume the initial specific volume of water (Vi) = Vw
The final specific volume of ice (Vf) = Vi + 0.091 cm^3
The work done during the expansion of water freezing into ice is given by the equation:
W = PΔV
Where:
W = work done
P = pressure
ΔV = change in specific volume
The work done is equal to the change in internal energy (U) of the system. Therefore,
U = W = PΔV
The change in internal energy is given by the equation:
U = Q - W
Where:
U = change in internal energy
Q = heat absorbed by the system
W = work done by the system
Since the water is freezing, the heat absorbed by the system (Q) is equal to the latent heat of ice (L). Therefore,
U = L - PΔV
Since the process is reversible, we can write:
U = TΔS
Where:
T = temperature in Kelvin
ΔS = change in entropy
The change in entropy is given by the equation:
ΔS = ΔQ / T
Since the process is isothermal, ΔQ = Q = L. Therefore,
ΔS = L / T
Substituting the values of U and ΔS, we get:
L / T = L - PΔV
PΔV = L - L / T
Simplifying the equation, we get:
P = (L - L / T) / ΔV
Substituting the given values, we get:
P = (80 x 4.2 x 10^7 - 80 x 4.2 x 10^7 / T) / 0.091
Step 4: Convert the temperature from Celsius to Kelvin
Given temperature = -10°C
- Change in specific volume when 1 gm of water freezes into ice = 0.091 cc
- Latent heat of ice = 80 cal/gm
- J = 4.2 x 10^7 ergs/cal
- 1 atmosphere = 10^6 dynes/cm^2
To find:
Pressure required to make water freeze at -10°C in atmospheres
Solution:
Step 1: Convert the change in specific volume from cc to cm^3
Given change in specific volume = 0.091 cc
1 cc = 1 cm^3
Therefore, change in specific volume = 0.091 cm^3
Step 2: Convert the latent heat of ice from calories to ergs
Given latent heat of ice = 80 cal/gm
1 cal = 4.2 x 10^7 ergs
Therefore, latent heat of ice = 80 x 4.2 x 10^7 ergs
Step 3: Calculate the pressure required to make water freeze at -10°C
The change in specific volume when water freezes into ice is given by the equation:
ΔV = Vf - Vi
Where:
ΔV = change in specific volume
Vf = final specific volume of ice
Vi = initial specific volume of water
Given ΔV = 0.091 cm^3
Let's assume the initial specific volume of water (Vi) = Vw
The final specific volume of ice (Vf) = Vi + 0.091 cm^3
The work done during the expansion of water freezing into ice is given by the equation:
W = PΔV
Where:
W = work done
P = pressure
ΔV = change in specific volume
The work done is equal to the change in internal energy (U) of the system. Therefore,
U = W = PΔV
The change in internal energy is given by the equation:
U = Q - W
Where:
U = change in internal energy
Q = heat absorbed by the system
W = work done by the system
Since the water is freezing, the heat absorbed by the system (Q) is equal to the latent heat of ice (L). Therefore,
U = L - PΔV
Since the process is reversible, we can write:
U = TΔS
Where:
T = temperature in Kelvin
ΔS = change in entropy
The change in entropy is given by the equation:
ΔS = ΔQ / T
Since the process is isothermal, ΔQ = Q = L. Therefore,
ΔS = L / T
Substituting the values of U and ΔS, we get:
L / T = L - PΔV
PΔV = L - L / T
Simplifying the equation, we get:
P = (L - L / T) / ΔV
Substituting the given values, we get:
P = (80 x 4.2 x 10^7 - 80 x 4.2 x 10^7 / T) / 0.091
Step 4: Convert the temperature from Celsius to Kelvin
Given temperature = -10°C
Free Test
FREE
| Start Free Test |
Community Answer
Calculate the pressure (in atmospheres) required to make water freeze ...
Given dT = 10C . V2 - V1 = -0.091 c.c.
L = 80 cal. = 80 * 4.2 * 107 ergs, T = 0 + 273 = 273 K
Applying Clapeyrons latent heat equation
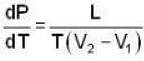
or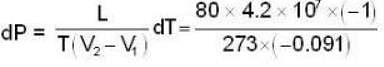
dynes/cm2.
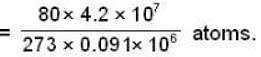
= 135.2 Atmos.
Hence to lower the melting of ice by 1°C, the pressure must be raised by 135.2 atmospheres.
Now melting point of ice at atmospheric pressure is 0°C. Hence pressure required to make ice freeze at - 1 °C
= 135.2 + 1 = 136.2 atmospheres
L = 80 cal. = 80 * 4.2 * 107 ergs, T = 0 + 273 = 273 K
Applying Clapeyrons latent heat equation
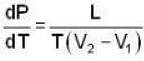
or
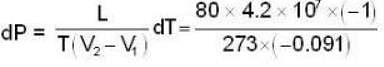dynes/cm2.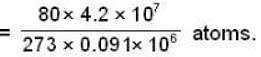= 135.2 Atmos.
Hence to lower the melting of ice by 1°C, the pressure must be raised by 135.2 atmospheres.
Now melting point of ice at atmospheric pressure is 0°C. Hence pressure required to make ice freeze at - 1 °C
= 135.2 + 1 = 136.2 atmospheres
|
Explore Courses for Physics exam
|
|
Similar Physics Doubts
Calculate the pressure (in atmospheres) required to make water freeze at - 10C. Change of specific volume when 1 gm of water freezes into ice = .091 cc.,J =4.2 x 107 ergs/cal..1 atmosphere 106 dynes / cm2 and the latent heat of ice = 80 cal./ gm.Correct answer is '136.2'. Can you explain this answer?
Question Description
Calculate the pressure (in atmospheres) required to make water freeze at - 10C. Change of specific volume when 1 gm of water freezes into ice = .091 cc.,J =4.2 x 107 ergs/cal..1 atmosphere 106 dynes / cm2 and the latent heat of ice = 80 cal./ gm.Correct answer is '136.2'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about Calculate the pressure (in atmospheres) required to make water freeze at - 10C. Change of specific volume when 1 gm of water freezes into ice = .091 cc.,J =4.2 x 107 ergs/cal..1 atmosphere 106 dynes / cm2 and the latent heat of ice = 80 cal./ gm.Correct answer is '136.2'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Calculate the pressure (in atmospheres) required to make water freeze at - 10C. Change of specific volume when 1 gm of water freezes into ice = .091 cc.,J =4.2 x 107 ergs/cal..1 atmosphere 106 dynes / cm2 and the latent heat of ice = 80 cal./ gm.Correct answer is '136.2'. Can you explain this answer?.
Calculate the pressure (in atmospheres) required to make water freeze at - 10C. Change of specific volume when 1 gm of water freezes into ice = .091 cc.,J =4.2 x 107 ergs/cal..1 atmosphere 106 dynes / cm2 and the latent heat of ice = 80 cal./ gm.Correct answer is '136.2'. Can you explain this answer? for Physics 2024 is part of Physics preparation. The Question and answers have been prepared according to the Physics exam syllabus. Information about Calculate the pressure (in atmospheres) required to make water freeze at - 10C. Change of specific volume when 1 gm of water freezes into ice = .091 cc.,J =4.2 x 107 ergs/cal..1 atmosphere 106 dynes / cm2 and the latent heat of ice = 80 cal./ gm.Correct answer is '136.2'. Can you explain this answer? covers all topics & solutions for Physics 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Calculate the pressure (in atmospheres) required to make water freeze at - 10C. Change of specific volume when 1 gm of water freezes into ice = .091 cc.,J =4.2 x 107 ergs/cal..1 atmosphere 106 dynes / cm2 and the latent heat of ice = 80 cal./ gm.Correct answer is '136.2'. Can you explain this answer?.
Solutions for Calculate the pressure (in atmospheres) required to make water freeze at - 10C. Change of specific volume when 1 gm of water freezes into ice = .091 cc.,J =4.2 x 107 ergs/cal..1 atmosphere 106 dynes / cm2 and the latent heat of ice = 80 cal./ gm.Correct answer is '136.2'. Can you explain this answer? in English & in Hindi are available as part of our courses for Physics.
Download more important topics, notes, lectures and mock test series for Physics Exam by signing up for free.
Here you can find the meaning of Calculate the pressure (in atmospheres) required to make water freeze at - 10C. Change of specific volume when 1 gm of water freezes into ice = .091 cc.,J =4.2 x 107 ergs/cal..1 atmosphere 106 dynes / cm2 and the latent heat of ice = 80 cal./ gm.Correct answer is '136.2'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Calculate the pressure (in atmospheres) required to make water freeze at - 10C. Change of specific volume when 1 gm of water freezes into ice = .091 cc.,J =4.2 x 107 ergs/cal..1 atmosphere 106 dynes / cm2 and the latent heat of ice = 80 cal./ gm.Correct answer is '136.2'. Can you explain this answer?, a detailed solution for Calculate the pressure (in atmospheres) required to make water freeze at - 10C. Change of specific volume when 1 gm of water freezes into ice = .091 cc.,J =4.2 x 107 ergs/cal..1 atmosphere 106 dynes / cm2 and the latent heat of ice = 80 cal./ gm.Correct answer is '136.2'. Can you explain this answer? has been provided alongside types of Calculate the pressure (in atmospheres) required to make water freeze at - 10C. Change of specific volume when 1 gm of water freezes into ice = .091 cc.,J =4.2 x 107 ergs/cal..1 atmosphere 106 dynes / cm2 and the latent heat of ice = 80 cal./ gm.Correct answer is '136.2'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Calculate the pressure (in atmospheres) required to make water freeze at - 10C. Change of specific volume when 1 gm of water freezes into ice = .091 cc.,J =4.2 x 107 ergs/cal..1 atmosphere 106 dynes / cm2 and the latent heat of ice = 80 cal./ gm.Correct answer is '136.2'. Can you explain this answer? tests, examples and also practice Physics tests.
|
|
Explore Courses for Physics exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup