GATE Exam > GATE Questions > One method of measuring the radius of an arc...
Start Learning for Free
One method of measuring the radius of an arc (R) is to allow a roller of radius (r) to oscillate to and fro on the arc and measure the average time per oscillation, T seconds. The roller will then have a linear acceleration of 2g/3, where g is the acceleration due to gravity. m such an experiment, the value of the radius of the arc can be found from the expression: (2002)
- a)(T2g / 6tπ2) + r
- b)(T2g / 6rπ2) - r
- c)(T2g / 6tπ2)
- d)(6r2 / T2g)
Correct answer is option 'A'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
One method of measuring the radius of an arc (R) is to allow a roller...
Time period,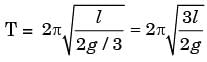
View all questions of this test
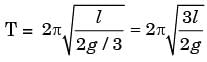
Where l = distance between centre of rolling to the centre of roll.
∴ 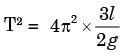
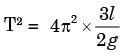
or 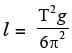
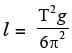
The radius of the arc, 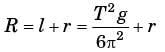
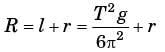
Most Upvoted Answer
One method of measuring the radius of an arc (R) is to allow a roller...
Time period,

Where l = distance between centre of rolling to the centre of roll.
∴ 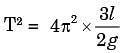
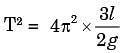
or 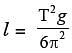
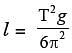
The radius of the arc, 

Free Test
FREE
| Start Free Test |
Community Answer
One method of measuring the radius of an arc (R) is to allow a roller...
Understanding the Experiment
The experiment involves a roller of radius 'r' oscillating along an arc of radius 'R'. The aim is to derive a formula to calculate 'R' based on the time period of oscillation 'T'.
Acceleration of the Roller
- The roller experiences a linear acceleration of 2g/3.
- This acceleration plays a crucial role in determining the motion of the roller on the arc.
Time Period of Oscillation
- The time period 'T' is a key measurement in this experiment.
- It reflects how long the roller takes to complete one oscillation along the arc.
Deriving the Expression
- The expression to find the radius of the arc can be derived by combining these elements.
- The correct formula incorporates terms that relate 'T', 'g', 'r', and 'R'.
Correct Option: A
- The correct answer is option 'A', which is derived from the relationship:
(2002)a)(T^2g / 6tπ^2) + rb)(T^2g / 6rπ^2) - rc)(T^2g / 6tπ^2)d)(6r^2 / T^2g).
- This formula effectively links the oscillation time, gravitational acceleration, and the radii involved.
Conclusion
- By analyzing the oscillation and acceleration, we can accurately determine the radius 'R' of the arc.
- This method is a practical application of physics principles in measuring curvilinear motion.
The experiment involves a roller of radius 'r' oscillating along an arc of radius 'R'. The aim is to derive a formula to calculate 'R' based on the time period of oscillation 'T'.
Acceleration of the Roller
- The roller experiences a linear acceleration of 2g/3.
- This acceleration plays a crucial role in determining the motion of the roller on the arc.
Time Period of Oscillation
- The time period 'T' is a key measurement in this experiment.
- It reflects how long the roller takes to complete one oscillation along the arc.
Deriving the Expression
- The expression to find the radius of the arc can be derived by combining these elements.
- The correct formula incorporates terms that relate 'T', 'g', 'r', and 'R'.
Correct Option: A
- The correct answer is option 'A', which is derived from the relationship:
(2002)a)(T^2g / 6tπ^2) + rb)(T^2g / 6rπ^2) - rc)(T^2g / 6tπ^2)d)(6r^2 / T^2g).
- This formula effectively links the oscillation time, gravitational acceleration, and the radii involved.
Conclusion
- By analyzing the oscillation and acceleration, we can accurately determine the radius 'R' of the arc.
- This method is a practical application of physics principles in measuring curvilinear motion.

|
Explore Courses for GATE exam
|

|
Similar GATE Doubts
One method of measuring the radius of an arc (R) is to allow a roller of radius (r) to oscillate to and fro on the arc and measure the average time per oscillation, T seconds. The roller will then have a linear acceleration of 2g/3, where g is the acceleration due to gravity. m such an experiment, the value of the radius of the arc can be found from the expression: (2002)a)(T2g / 6tπ2) + rb)(T2g / 6rπ2) - rc)(T2g / 6tπ2)d)(6r2 / T2g)Correct answer is option 'A'. Can you explain this answer?
Question Description
One method of measuring the radius of an arc (R) is to allow a roller of radius (r) to oscillate to and fro on the arc and measure the average time per oscillation, T seconds. The roller will then have a linear acceleration of 2g/3, where g is the acceleration due to gravity. m such an experiment, the value of the radius of the arc can be found from the expression: (2002)a)(T2g / 6tπ2) + rb)(T2g / 6rπ2) - rc)(T2g / 6tπ2)d)(6r2 / T2g)Correct answer is option 'A'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about One method of measuring the radius of an arc (R) is to allow a roller of radius (r) to oscillate to and fro on the arc and measure the average time per oscillation, T seconds. The roller will then have a linear acceleration of 2g/3, where g is the acceleration due to gravity. m such an experiment, the value of the radius of the arc can be found from the expression: (2002)a)(T2g / 6tπ2) + rb)(T2g / 6rπ2) - rc)(T2g / 6tπ2)d)(6r2 / T2g)Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for One method of measuring the radius of an arc (R) is to allow a roller of radius (r) to oscillate to and fro on the arc and measure the average time per oscillation, T seconds. The roller will then have a linear acceleration of 2g/3, where g is the acceleration due to gravity. m such an experiment, the value of the radius of the arc can be found from the expression: (2002)a)(T2g / 6tπ2) + rb)(T2g / 6rπ2) - rc)(T2g / 6tπ2)d)(6r2 / T2g)Correct answer is option 'A'. Can you explain this answer?.
One method of measuring the radius of an arc (R) is to allow a roller of radius (r) to oscillate to and fro on the arc and measure the average time per oscillation, T seconds. The roller will then have a linear acceleration of 2g/3, where g is the acceleration due to gravity. m such an experiment, the value of the radius of the arc can be found from the expression: (2002)a)(T2g / 6tπ2) + rb)(T2g / 6rπ2) - rc)(T2g / 6tπ2)d)(6r2 / T2g)Correct answer is option 'A'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about One method of measuring the radius of an arc (R) is to allow a roller of radius (r) to oscillate to and fro on the arc and measure the average time per oscillation, T seconds. The roller will then have a linear acceleration of 2g/3, where g is the acceleration due to gravity. m such an experiment, the value of the radius of the arc can be found from the expression: (2002)a)(T2g / 6tπ2) + rb)(T2g / 6rπ2) - rc)(T2g / 6tπ2)d)(6r2 / T2g)Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for One method of measuring the radius of an arc (R) is to allow a roller of radius (r) to oscillate to and fro on the arc and measure the average time per oscillation, T seconds. The roller will then have a linear acceleration of 2g/3, where g is the acceleration due to gravity. m such an experiment, the value of the radius of the arc can be found from the expression: (2002)a)(T2g / 6tπ2) + rb)(T2g / 6rπ2) - rc)(T2g / 6tπ2)d)(6r2 / T2g)Correct answer is option 'A'. Can you explain this answer?.
Solutions for One method of measuring the radius of an arc (R) is to allow a roller of radius (r) to oscillate to and fro on the arc and measure the average time per oscillation, T seconds. The roller will then have a linear acceleration of 2g/3, where g is the acceleration due to gravity. m such an experiment, the value of the radius of the arc can be found from the expression: (2002)a)(T2g / 6tπ2) + rb)(T2g / 6rπ2) - rc)(T2g / 6tπ2)d)(6r2 / T2g)Correct answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for GATE.
Download more important topics, notes, lectures and mock test series for GATE Exam by signing up for free.
Here you can find the meaning of One method of measuring the radius of an arc (R) is to allow a roller of radius (r) to oscillate to and fro on the arc and measure the average time per oscillation, T seconds. The roller will then have a linear acceleration of 2g/3, where g is the acceleration due to gravity. m such an experiment, the value of the radius of the arc can be found from the expression: (2002)a)(T2g / 6tπ2) + rb)(T2g / 6rπ2) - rc)(T2g / 6tπ2)d)(6r2 / T2g)Correct answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
One method of measuring the radius of an arc (R) is to allow a roller of radius (r) to oscillate to and fro on the arc and measure the average time per oscillation, T seconds. The roller will then have a linear acceleration of 2g/3, where g is the acceleration due to gravity. m such an experiment, the value of the radius of the arc can be found from the expression: (2002)a)(T2g / 6tπ2) + rb)(T2g / 6rπ2) - rc)(T2g / 6tπ2)d)(6r2 / T2g)Correct answer is option 'A'. Can you explain this answer?, a detailed solution for One method of measuring the radius of an arc (R) is to allow a roller of radius (r) to oscillate to and fro on the arc and measure the average time per oscillation, T seconds. The roller will then have a linear acceleration of 2g/3, where g is the acceleration due to gravity. m such an experiment, the value of the radius of the arc can be found from the expression: (2002)a)(T2g / 6tπ2) + rb)(T2g / 6rπ2) - rc)(T2g / 6tπ2)d)(6r2 / T2g)Correct answer is option 'A'. Can you explain this answer? has been provided alongside types of One method of measuring the radius of an arc (R) is to allow a roller of radius (r) to oscillate to and fro on the arc and measure the average time per oscillation, T seconds. The roller will then have a linear acceleration of 2g/3, where g is the acceleration due to gravity. m such an experiment, the value of the radius of the arc can be found from the expression: (2002)a)(T2g / 6tπ2) + rb)(T2g / 6rπ2) - rc)(T2g / 6tπ2)d)(6r2 / T2g)Correct answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice One method of measuring the radius of an arc (R) is to allow a roller of radius (r) to oscillate to and fro on the arc and measure the average time per oscillation, T seconds. The roller will then have a linear acceleration of 2g/3, where g is the acceleration due to gravity. m such an experiment, the value of the radius of the arc can be found from the expression: (2002)a)(T2g / 6tπ2) + rb)(T2g / 6rπ2) - rc)(T2g / 6tπ2)d)(6r2 / T2g)Correct answer is option 'A'. Can you explain this answer? tests, examples and also practice GATE tests.

|
Explore Courses for GATE exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















