SSC Exam > SSC Questions > The deflection of a simply supported rectang...
Start Learning for Free
The deflection of a simply supported rectangular beam is:
- a)directly proportional to the cube of its length
- b)inversely proportional to the cube of its depth
- c)inversely proportional to its width
- d)all of the above
Correct answer is option 'D'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
The deflection of a simply supported rectangular beam is:a)directly p...
Deflection of simply supported beam
View all questions of this test
Concentrated load P at the center, 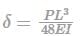
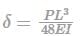
Uniformly distributed load w (N/m), 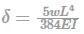
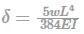
I = bd3/12
Most Upvoted Answer
The deflection of a simply supported rectangular beam is:a)directly p...
The deflection of a simply supported rectangular beam is influenced by various factors such as length, depth, and width of the beam. Let's analyze each option to understand their impact on the deflection of the beam.
a) Directly proportional to the cube of its length:
When the length of a beam increases, the deflection also increases. This relationship is not linear but cubic. The deflection is directly proportional to the cube of the length. This means that if the length of the beam is doubled, the deflection will increase by a factor of 8 (2^3). Similarly, if the length is tripled, the deflection will increase by a factor of 27 (3^3).
b) Inversely proportional to the cube of its depth:
The depth of a beam refers to the dimension perpendicular to the length and width. When the depth of a beam increases, the deflection decreases. This relationship is also not linear but inverse cubic. The deflection is inversely proportional to the cube of the depth. If the depth is doubled, the deflection will decrease by a factor of 8 (2^3). Similarly, if the depth is tripled, the deflection will decrease by a factor of 27 (3^3).
c) Inversely proportional to its width:
The width of a beam refers to the dimension perpendicular to the length and depth. When the width of a beam increases, the deflection decreases. This relationship is inverse, but not cubic. The deflection is inversely proportional to the width. If the width is doubled, the deflection will decrease by a factor of 2. Similarly, if the width is tripled, the deflection will decrease by a factor of 3.
d) All of the above:
Considering the above explanations, we can conclude that all the given options are correct. The deflection of a simply supported rectangular beam is directly proportional to the cube of its length, inversely proportional to the cube of its depth, and inversely proportional to its width.
In summary, the deflection of a simply supported rectangular beam is influenced by its length, depth, and width. The relationships between these factors and the deflection are not linear, but cubic or inverse. These relationships are derived from the principles of structural mechanics and are widely used in engineering calculations and design.
a) Directly proportional to the cube of its length:
When the length of a beam increases, the deflection also increases. This relationship is not linear but cubic. The deflection is directly proportional to the cube of the length. This means that if the length of the beam is doubled, the deflection will increase by a factor of 8 (2^3). Similarly, if the length is tripled, the deflection will increase by a factor of 27 (3^3).
b) Inversely proportional to the cube of its depth:
The depth of a beam refers to the dimension perpendicular to the length and width. When the depth of a beam increases, the deflection decreases. This relationship is also not linear but inverse cubic. The deflection is inversely proportional to the cube of the depth. If the depth is doubled, the deflection will decrease by a factor of 8 (2^3). Similarly, if the depth is tripled, the deflection will decrease by a factor of 27 (3^3).
c) Inversely proportional to its width:
The width of a beam refers to the dimension perpendicular to the length and depth. When the width of a beam increases, the deflection decreases. This relationship is inverse, but not cubic. The deflection is inversely proportional to the width. If the width is doubled, the deflection will decrease by a factor of 2. Similarly, if the width is tripled, the deflection will decrease by a factor of 3.
d) All of the above:
Considering the above explanations, we can conclude that all the given options are correct. The deflection of a simply supported rectangular beam is directly proportional to the cube of its length, inversely proportional to the cube of its depth, and inversely proportional to its width.
In summary, the deflection of a simply supported rectangular beam is influenced by its length, depth, and width. The relationships between these factors and the deflection are not linear, but cubic or inverse. These relationships are derived from the principles of structural mechanics and are widely used in engineering calculations and design.
Free Test
FREE
| Start Free Test |
Community Answer
The deflection of a simply supported rectangular beam is:a)directly p...
Deflection of simply supported beam
Concentrated load P at the center, 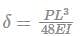
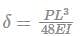
Uniformly distributed load w (N/m), 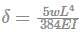
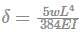
I = bd3/12

|
Explore Courses for SSC exam
|

|
Similar SSC Doubts
The deflection of a simply supported rectangular beam is:a)directly proportional to the cube of its lengthb)inversely proportional to the cube of its depthc)inversely proportional to its widthd)all of the aboveCorrect answer is option 'D'. Can you explain this answer?
Question Description
The deflection of a simply supported rectangular beam is:a)directly proportional to the cube of its lengthb)inversely proportional to the cube of its depthc)inversely proportional to its widthd)all of the aboveCorrect answer is option 'D'. Can you explain this answer? for SSC 2024 is part of SSC preparation. The Question and answers have been prepared according to the SSC exam syllabus. Information about The deflection of a simply supported rectangular beam is:a)directly proportional to the cube of its lengthb)inversely proportional to the cube of its depthc)inversely proportional to its widthd)all of the aboveCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for SSC 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The deflection of a simply supported rectangular beam is:a)directly proportional to the cube of its lengthb)inversely proportional to the cube of its depthc)inversely proportional to its widthd)all of the aboveCorrect answer is option 'D'. Can you explain this answer?.
The deflection of a simply supported rectangular beam is:a)directly proportional to the cube of its lengthb)inversely proportional to the cube of its depthc)inversely proportional to its widthd)all of the aboveCorrect answer is option 'D'. Can you explain this answer? for SSC 2024 is part of SSC preparation. The Question and answers have been prepared according to the SSC exam syllabus. Information about The deflection of a simply supported rectangular beam is:a)directly proportional to the cube of its lengthb)inversely proportional to the cube of its depthc)inversely proportional to its widthd)all of the aboveCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for SSC 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The deflection of a simply supported rectangular beam is:a)directly proportional to the cube of its lengthb)inversely proportional to the cube of its depthc)inversely proportional to its widthd)all of the aboveCorrect answer is option 'D'. Can you explain this answer?.
Solutions for The deflection of a simply supported rectangular beam is:a)directly proportional to the cube of its lengthb)inversely proportional to the cube of its depthc)inversely proportional to its widthd)all of the aboveCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for SSC.
Download more important topics, notes, lectures and mock test series for SSC Exam by signing up for free.
Here you can find the meaning of The deflection of a simply supported rectangular beam is:a)directly proportional to the cube of its lengthb)inversely proportional to the cube of its depthc)inversely proportional to its widthd)all of the aboveCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The deflection of a simply supported rectangular beam is:a)directly proportional to the cube of its lengthb)inversely proportional to the cube of its depthc)inversely proportional to its widthd)all of the aboveCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for The deflection of a simply supported rectangular beam is:a)directly proportional to the cube of its lengthb)inversely proportional to the cube of its depthc)inversely proportional to its widthd)all of the aboveCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of The deflection of a simply supported rectangular beam is:a)directly proportional to the cube of its lengthb)inversely proportional to the cube of its depthc)inversely proportional to its widthd)all of the aboveCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The deflection of a simply supported rectangular beam is:a)directly proportional to the cube of its lengthb)inversely proportional to the cube of its depthc)inversely proportional to its widthd)all of the aboveCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice SSC tests.

|
Explore Courses for SSC exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















