SSC Exam > SSC Questions > Which of the following related fluid flow pa...
Start Learning for Free
Which of the following related fluid flow parameters exist both in rotational and irrotational flows?
- a)Vorticity
- b)Stream function
- c)Velocity potential
- d)Both Vorticity and Stream function
Correct answer is option 'B'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Which of the following related fluid flow parameters exist both in ro...
Velocity potential function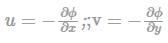
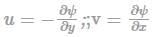
View all questions of this test
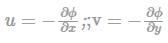
(i) If velocity potential (ϕ) exists, the flow should be irrotational.
(ii) If velocity potential (ϕ) satisfies the Laplace equation, it represents the possible steady incompressible irrotational flow.
Stream function:
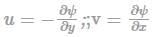
(i) If stream function (ψ) exists, the flow may be rotational or irrotational.
(ii) If stream function (ψ) satisfies the Laplace equation, it represents the irrotational flow.
Vorticity:
Defined as the value twice of the rotation
ζ=2ω
For an irrotational flow, vorticity components are zero
Most Upvoted Answer
Which of the following related fluid flow parameters exist both in ro...
Stream function:
The stream function is a mathematical function used to describe the flow of a fluid in two dimensions. It is defined such that its partial derivatives with respect to the coordinates of a point give the velocities at that point. In other words, it can be used to determine the flow velocity components in a fluid flow field. The stream function is commonly used to describe irrotational flows, where the fluid particles move in smooth, organized paths with no rotation.
Velocity potential:
The velocity potential is another mathematical function used to describe fluid flow. It is defined such that its gradient gives the velocity vector at each point in the flow field. The velocity potential is also commonly used to describe irrotational flows, where the fluid particles move in smooth paths without any rotation.
Vorticity:
Vorticity is a measure of the local rotation of a fluid flow. It is defined as the curl of the velocity vector field. In other words, it represents the tendency of fluid elements to rotate about their own axes. Vorticity is non-zero in rotational flows, where the fluid particles have both translational and rotational motion.
Explanation:
In rotational flows, the fluid particles have both translational and rotational motion, so vorticity is non-zero. The presence of vorticity indicates the presence of circulation and rotation in the flow.
However, in irrotational flows, the fluid particles move in smooth, organized paths with no rotation. This means that vorticity is zero in irrotational flows.
Both the stream function and the velocity potential are mathematical functions commonly used to describe fluid flow. They are particularly useful in describing irrotational flows, where the fluid particles move in smooth paths without any rotation.
Therefore, the correct answer is option 'B': Both the stream function and the velocity potential exist in both rotational and irrotational flows.
The stream function is a mathematical function used to describe the flow of a fluid in two dimensions. It is defined such that its partial derivatives with respect to the coordinates of a point give the velocities at that point. In other words, it can be used to determine the flow velocity components in a fluid flow field. The stream function is commonly used to describe irrotational flows, where the fluid particles move in smooth, organized paths with no rotation.
Velocity potential:
The velocity potential is another mathematical function used to describe fluid flow. It is defined such that its gradient gives the velocity vector at each point in the flow field. The velocity potential is also commonly used to describe irrotational flows, where the fluid particles move in smooth paths without any rotation.
Vorticity:
Vorticity is a measure of the local rotation of a fluid flow. It is defined as the curl of the velocity vector field. In other words, it represents the tendency of fluid elements to rotate about their own axes. Vorticity is non-zero in rotational flows, where the fluid particles have both translational and rotational motion.
Explanation:
In rotational flows, the fluid particles have both translational and rotational motion, so vorticity is non-zero. The presence of vorticity indicates the presence of circulation and rotation in the flow.
However, in irrotational flows, the fluid particles move in smooth, organized paths with no rotation. This means that vorticity is zero in irrotational flows.
Both the stream function and the velocity potential are mathematical functions commonly used to describe fluid flow. They are particularly useful in describing irrotational flows, where the fluid particles move in smooth paths without any rotation.
Therefore, the correct answer is option 'B': Both the stream function and the velocity potential exist in both rotational and irrotational flows.

|
Explore Courses for SSC exam
|

|
Similar SSC Doubts
Which of the following related fluid flow parameters exist both in rotational and irrotational flows?a)Vorticityb)Stream functionc)Velocity potentiald)Both Vorticity and Stream functionCorrect answer is option 'B'. Can you explain this answer?
Question Description
Which of the following related fluid flow parameters exist both in rotational and irrotational flows?a)Vorticityb)Stream functionc)Velocity potentiald)Both Vorticity and Stream functionCorrect answer is option 'B'. Can you explain this answer? for SSC 2024 is part of SSC preparation. The Question and answers have been prepared according to the SSC exam syllabus. Information about Which of the following related fluid flow parameters exist both in rotational and irrotational flows?a)Vorticityb)Stream functionc)Velocity potentiald)Both Vorticity and Stream functionCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for SSC 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Which of the following related fluid flow parameters exist both in rotational and irrotational flows?a)Vorticityb)Stream functionc)Velocity potentiald)Both Vorticity and Stream functionCorrect answer is option 'B'. Can you explain this answer?.
Which of the following related fluid flow parameters exist both in rotational and irrotational flows?a)Vorticityb)Stream functionc)Velocity potentiald)Both Vorticity and Stream functionCorrect answer is option 'B'. Can you explain this answer? for SSC 2024 is part of SSC preparation. The Question and answers have been prepared according to the SSC exam syllabus. Information about Which of the following related fluid flow parameters exist both in rotational and irrotational flows?a)Vorticityb)Stream functionc)Velocity potentiald)Both Vorticity and Stream functionCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for SSC 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Which of the following related fluid flow parameters exist both in rotational and irrotational flows?a)Vorticityb)Stream functionc)Velocity potentiald)Both Vorticity and Stream functionCorrect answer is option 'B'. Can you explain this answer?.
Solutions for Which of the following related fluid flow parameters exist both in rotational and irrotational flows?a)Vorticityb)Stream functionc)Velocity potentiald)Both Vorticity and Stream functionCorrect answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for SSC.
Download more important topics, notes, lectures and mock test series for SSC Exam by signing up for free.
Here you can find the meaning of Which of the following related fluid flow parameters exist both in rotational and irrotational flows?a)Vorticityb)Stream functionc)Velocity potentiald)Both Vorticity and Stream functionCorrect answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Which of the following related fluid flow parameters exist both in rotational and irrotational flows?a)Vorticityb)Stream functionc)Velocity potentiald)Both Vorticity and Stream functionCorrect answer is option 'B'. Can you explain this answer?, a detailed solution for Which of the following related fluid flow parameters exist both in rotational and irrotational flows?a)Vorticityb)Stream functionc)Velocity potentiald)Both Vorticity and Stream functionCorrect answer is option 'B'. Can you explain this answer? has been provided alongside types of Which of the following related fluid flow parameters exist both in rotational and irrotational flows?a)Vorticityb)Stream functionc)Velocity potentiald)Both Vorticity and Stream functionCorrect answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Which of the following related fluid flow parameters exist both in rotational and irrotational flows?a)Vorticityb)Stream functionc)Velocity potentiald)Both Vorticity and Stream functionCorrect answer is option 'B'. Can you explain this answer? tests, examples and also practice SSC tests.

|
Explore Courses for SSC exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















