SSC Exam > SSC Questions > A moving coil instrument has a resistance of...
Start Learning for Free
A moving coil instrument has a resistance of 10 and gives full-scale deflection at 0.5 V potential difference across it. How can it be adapted to measure a current upto 100 A ?
- a)by connecting shunt resistance of across the meter
- b)by connecting shunt resistance of across the meter
- c)by connecting shunt resistance of across the meter
- d)by connecting shunt resistance of across the meter
Correct answer is option 'A'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A moving coil instrument has a resistance of 10 and gives full-scale ...




Most Upvoted Answer
A moving coil instrument has a resistance of 10 and gives full-scale ...
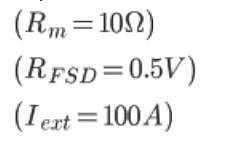

Free Test
FREE
| Start Free Test |
Community Answer
A moving coil instrument has a resistance of 10 and gives full-scale ...
To adapt a moving coil instrument to measure a current up to 100 A, a shunt resistance needs to be connected across the meter. The correct option is A.
Explanation:
A shunt resistance is used to divert a portion of the current away from the moving coil instrument, allowing it to measure higher currents without getting damaged.
Here's how it works:
1. Understanding the problem:
- The moving coil instrument has a resistance of 10 ohms.
- It gives a full-scale deflection at 0.5 V potential difference across it.
- We need to measure currents up to 100 A.
2. Calculating the shunt resistance:
- The full-scale deflection across the instrument occurs at 0.5 V.
- Since the resistance of the instrument is 10 ohms, the current required for full-scale deflection is I = V/R = 0.5/10 = 0.05 A (50 mA).
- To measure currents up to 100 A, we need to divert most of the current away from the instrument.
- Let's assume we want the instrument to read full-scale deflection at 100 A. Therefore, the shunt resistance should be designed to create a voltage drop of 0.5 V at 100 A.
- Using Ohm's law (V = IR), we can calculate the required resistance: R = V/I = 0.5/100 = 0.005 ohms (5 mΩ).
3. Connecting the shunt resistance:
- The shunt resistance (0.005 ohms) is connected in parallel with the moving coil instrument.
- This means that most of the current will pass through the shunt resistance, while a small portion will pass through the instrument.
- The instrument will measure the voltage drop across its terminals, which is proportional to the current passing through it.
- By calibrating the instrument, we can ensure that full-scale deflection occurs at 0.5 V, corresponding to 100 A passing through the shunt resistance.
In summary, by connecting a shunt resistance of 0.005 ohms across the moving coil instrument, it can be adapted to measure currents up to 100 A.
Explanation:
A shunt resistance is used to divert a portion of the current away from the moving coil instrument, allowing it to measure higher currents without getting damaged.
Here's how it works:
1. Understanding the problem:
- The moving coil instrument has a resistance of 10 ohms.
- It gives a full-scale deflection at 0.5 V potential difference across it.
- We need to measure currents up to 100 A.
2. Calculating the shunt resistance:
- The full-scale deflection across the instrument occurs at 0.5 V.
- Since the resistance of the instrument is 10 ohms, the current required for full-scale deflection is I = V/R = 0.5/10 = 0.05 A (50 mA).
- To measure currents up to 100 A, we need to divert most of the current away from the instrument.
- Let's assume we want the instrument to read full-scale deflection at 100 A. Therefore, the shunt resistance should be designed to create a voltage drop of 0.5 V at 100 A.
- Using Ohm's law (V = IR), we can calculate the required resistance: R = V/I = 0.5/100 = 0.005 ohms (5 mΩ).
3. Connecting the shunt resistance:
- The shunt resistance (0.005 ohms) is connected in parallel with the moving coil instrument.
- This means that most of the current will pass through the shunt resistance, while a small portion will pass through the instrument.
- The instrument will measure the voltage drop across its terminals, which is proportional to the current passing through it.
- By calibrating the instrument, we can ensure that full-scale deflection occurs at 0.5 V, corresponding to 100 A passing through the shunt resistance.
In summary, by connecting a shunt resistance of 0.005 ohms across the moving coil instrument, it can be adapted to measure currents up to 100 A.

|
Explore Courses for SSC exam
|

|
Similar SSC Doubts
A moving coil instrument has a resistance of 10 and gives full-scale deflection at 0.5 V potential difference across it. How can it be adapted to measure a current upto 100 A ?a)by connecting shunt resistance of across the meterb)by connecting shunt resistance of across the meterc)by connecting shunt resistance of across the meterd)by connecting shunt resistance of across the meterCorrect answer is option 'A'. Can you explain this answer?
Question Description
A moving coil instrument has a resistance of 10 and gives full-scale deflection at 0.5 V potential difference across it. How can it be adapted to measure a current upto 100 A ?a)by connecting shunt resistance of across the meterb)by connecting shunt resistance of across the meterc)by connecting shunt resistance of across the meterd)by connecting shunt resistance of across the meterCorrect answer is option 'A'. Can you explain this answer? for SSC 2024 is part of SSC preparation. The Question and answers have been prepared according to the SSC exam syllabus. Information about A moving coil instrument has a resistance of 10 and gives full-scale deflection at 0.5 V potential difference across it. How can it be adapted to measure a current upto 100 A ?a)by connecting shunt resistance of across the meterb)by connecting shunt resistance of across the meterc)by connecting shunt resistance of across the meterd)by connecting shunt resistance of across the meterCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for SSC 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A moving coil instrument has a resistance of 10 and gives full-scale deflection at 0.5 V potential difference across it. How can it be adapted to measure a current upto 100 A ?a)by connecting shunt resistance of across the meterb)by connecting shunt resistance of across the meterc)by connecting shunt resistance of across the meterd)by connecting shunt resistance of across the meterCorrect answer is option 'A'. Can you explain this answer?.
A moving coil instrument has a resistance of 10 and gives full-scale deflection at 0.5 V potential difference across it. How can it be adapted to measure a current upto 100 A ?a)by connecting shunt resistance of across the meterb)by connecting shunt resistance of across the meterc)by connecting shunt resistance of across the meterd)by connecting shunt resistance of across the meterCorrect answer is option 'A'. Can you explain this answer? for SSC 2024 is part of SSC preparation. The Question and answers have been prepared according to the SSC exam syllabus. Information about A moving coil instrument has a resistance of 10 and gives full-scale deflection at 0.5 V potential difference across it. How can it be adapted to measure a current upto 100 A ?a)by connecting shunt resistance of across the meterb)by connecting shunt resistance of across the meterc)by connecting shunt resistance of across the meterd)by connecting shunt resistance of across the meterCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for SSC 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A moving coil instrument has a resistance of 10 and gives full-scale deflection at 0.5 V potential difference across it. How can it be adapted to measure a current upto 100 A ?a)by connecting shunt resistance of across the meterb)by connecting shunt resistance of across the meterc)by connecting shunt resistance of across the meterd)by connecting shunt resistance of across the meterCorrect answer is option 'A'. Can you explain this answer?.
Solutions for A moving coil instrument has a resistance of 10 and gives full-scale deflection at 0.5 V potential difference across it. How can it be adapted to measure a current upto 100 A ?a)by connecting shunt resistance of across the meterb)by connecting shunt resistance of across the meterc)by connecting shunt resistance of across the meterd)by connecting shunt resistance of across the meterCorrect answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for SSC.
Download more important topics, notes, lectures and mock test series for SSC Exam by signing up for free.
Here you can find the meaning of A moving coil instrument has a resistance of 10 and gives full-scale deflection at 0.5 V potential difference across it. How can it be adapted to measure a current upto 100 A ?a)by connecting shunt resistance of across the meterb)by connecting shunt resistance of across the meterc)by connecting shunt resistance of across the meterd)by connecting shunt resistance of across the meterCorrect answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A moving coil instrument has a resistance of 10 and gives full-scale deflection at 0.5 V potential difference across it. How can it be adapted to measure a current upto 100 A ?a)by connecting shunt resistance of across the meterb)by connecting shunt resistance of across the meterc)by connecting shunt resistance of across the meterd)by connecting shunt resistance of across the meterCorrect answer is option 'A'. Can you explain this answer?, a detailed solution for A moving coil instrument has a resistance of 10 and gives full-scale deflection at 0.5 V potential difference across it. How can it be adapted to measure a current upto 100 A ?a)by connecting shunt resistance of across the meterb)by connecting shunt resistance of across the meterc)by connecting shunt resistance of across the meterd)by connecting shunt resistance of across the meterCorrect answer is option 'A'. Can you explain this answer? has been provided alongside types of A moving coil instrument has a resistance of 10 and gives full-scale deflection at 0.5 V potential difference across it. How can it be adapted to measure a current upto 100 A ?a)by connecting shunt resistance of across the meterb)by connecting shunt resistance of across the meterc)by connecting shunt resistance of across the meterd)by connecting shunt resistance of across the meterCorrect answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A moving coil instrument has a resistance of 10 and gives full-scale deflection at 0.5 V potential difference across it. How can it be adapted to measure a current upto 100 A ?a)by connecting shunt resistance of across the meterb)by connecting shunt resistance of across the meterc)by connecting shunt resistance of across the meterd)by connecting shunt resistance of across the meterCorrect answer is option 'A'. Can you explain this answer? tests, examples and also practice SSC tests.

|
Explore Courses for SSC exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















