SSC Exam > SSC Questions > In the case of the bi-axial state of normal ...
Start Learning for Free
In the case of the bi-axial state of normal stresses, the normal stress on 45° plane is equal to
- a)the sum of the normal stresses
- b)difference of the normal stresses
- c)half the sum of the normal stresses
- d)half the difference of the normal stresses
Correct answer is option 'C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
In the case of the bi-axial state of normal stresses, the normal stre...
In the case of the bi-axial state of normal stresses:
Normal stress on an inclined plane:
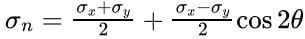
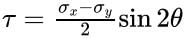
Shear Stress on an inclined plane:
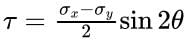
Normal stress on 45° plane:
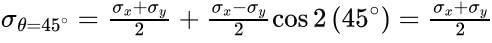
Most Upvoted Answer
In the case of the bi-axial state of normal stresses, the normal stre...
Understanding Bi-Axial State of Normal Stresses
In a bi-axial state of normal stresses, we have two perpendicular normal stresses acting on a material. Let's denote these stresses as σ1 and σ2. The analysis of stresses on a plane inclined at 45° helps in understanding the resultant stress conditions.
Normal Stress on 45° Plane
To find the normal stress acting on a plane that is oriented at 45°, we utilize the transformation equations for normal and shear stresses. Specifically, the normal stress on this 45° plane can be derived from the following relationship:
- The normal stress (σ45) on a plane inclined at 45° is given by the average of the two principal stresses.
Formula for Normal Stress on 45° Plane
- The equation can be simplified to express σ45 as:
σ45 = (σ1 + σ2) / 2
This indicates that the normal stress on a 45° plane is essentially half the sum of the two principal stresses acting on the material.
Conclusion
Thus, the correct answer to the question regarding the normal stress on a 45° plane in a bi-axial state of normal stresses is:
- Option C: Half the sum of the normal stresses
This conclusion stems from the fundamental principles of stress transformation, highlighting how stresses behave under different orientations in materials subjected to loading. Understanding this concept is crucial for engineers and designers to ensure the integrity and safety of structures under various loading conditions.
In a bi-axial state of normal stresses, we have two perpendicular normal stresses acting on a material. Let's denote these stresses as σ1 and σ2. The analysis of stresses on a plane inclined at 45° helps in understanding the resultant stress conditions.
Normal Stress on 45° Plane
To find the normal stress acting on a plane that is oriented at 45°, we utilize the transformation equations for normal and shear stresses. Specifically, the normal stress on this 45° plane can be derived from the following relationship:
- The normal stress (σ45) on a plane inclined at 45° is given by the average of the two principal stresses.
Formula for Normal Stress on 45° Plane
- The equation can be simplified to express σ45 as:
σ45 = (σ1 + σ2) / 2
This indicates that the normal stress on a 45° plane is essentially half the sum of the two principal stresses acting on the material.
Conclusion
Thus, the correct answer to the question regarding the normal stress on a 45° plane in a bi-axial state of normal stresses is:
- Option C: Half the sum of the normal stresses
This conclusion stems from the fundamental principles of stress transformation, highlighting how stresses behave under different orientations in materials subjected to loading. Understanding this concept is crucial for engineers and designers to ensure the integrity and safety of structures under various loading conditions.

|
Explore Courses for SSC exam
|

|
Similar SSC Doubts
In the case of the bi-axial state of normal stresses, the normal stress on 45° plane is equal toa)the sum of the normal stressesb)difference of the normal stressesc)half the sum of the normal stressesd)half the difference of the normal stressesCorrect answer is option 'C'. Can you explain this answer?
Question Description
In the case of the bi-axial state of normal stresses, the normal stress on 45° plane is equal toa)the sum of the normal stressesb)difference of the normal stressesc)half the sum of the normal stressesd)half the difference of the normal stressesCorrect answer is option 'C'. Can you explain this answer? for SSC 2024 is part of SSC preparation. The Question and answers have been prepared according to the SSC exam syllabus. Information about In the case of the bi-axial state of normal stresses, the normal stress on 45° plane is equal toa)the sum of the normal stressesb)difference of the normal stressesc)half the sum of the normal stressesd)half the difference of the normal stressesCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for SSC 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for In the case of the bi-axial state of normal stresses, the normal stress on 45° plane is equal toa)the sum of the normal stressesb)difference of the normal stressesc)half the sum of the normal stressesd)half the difference of the normal stressesCorrect answer is option 'C'. Can you explain this answer?.
In the case of the bi-axial state of normal stresses, the normal stress on 45° plane is equal toa)the sum of the normal stressesb)difference of the normal stressesc)half the sum of the normal stressesd)half the difference of the normal stressesCorrect answer is option 'C'. Can you explain this answer? for SSC 2024 is part of SSC preparation. The Question and answers have been prepared according to the SSC exam syllabus. Information about In the case of the bi-axial state of normal stresses, the normal stress on 45° plane is equal toa)the sum of the normal stressesb)difference of the normal stressesc)half the sum of the normal stressesd)half the difference of the normal stressesCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for SSC 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for In the case of the bi-axial state of normal stresses, the normal stress on 45° plane is equal toa)the sum of the normal stressesb)difference of the normal stressesc)half the sum of the normal stressesd)half the difference of the normal stressesCorrect answer is option 'C'. Can you explain this answer?.
Solutions for In the case of the bi-axial state of normal stresses, the normal stress on 45° plane is equal toa)the sum of the normal stressesb)difference of the normal stressesc)half the sum of the normal stressesd)half the difference of the normal stressesCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for SSC.
Download more important topics, notes, lectures and mock test series for SSC Exam by signing up for free.
Here you can find the meaning of In the case of the bi-axial state of normal stresses, the normal stress on 45° plane is equal toa)the sum of the normal stressesb)difference of the normal stressesc)half the sum of the normal stressesd)half the difference of the normal stressesCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
In the case of the bi-axial state of normal stresses, the normal stress on 45° plane is equal toa)the sum of the normal stressesb)difference of the normal stressesc)half the sum of the normal stressesd)half the difference of the normal stressesCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for In the case of the bi-axial state of normal stresses, the normal stress on 45° plane is equal toa)the sum of the normal stressesb)difference of the normal stressesc)half the sum of the normal stressesd)half the difference of the normal stressesCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of In the case of the bi-axial state of normal stresses, the normal stress on 45° plane is equal toa)the sum of the normal stressesb)difference of the normal stressesc)half the sum of the normal stressesd)half the difference of the normal stressesCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice In the case of the bi-axial state of normal stresses, the normal stress on 45° plane is equal toa)the sum of the normal stressesb)difference of the normal stressesc)half the sum of the normal stressesd)half the difference of the normal stressesCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice SSC tests.

|
Explore Courses for SSC exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















