SSC Exam > SSC Questions > A cylindrical elastic body subjected to pure...
Start Learning for Free
A cylindrical elastic body subjected to pure torsion about its axis develops
- a)Tensile stress in a direction 45° to the axis
- b)No tensile or compressive stress
- c)Maximum shear stress along the axis of the shaft
- d)Maximum shear stress at 45° to the axis
Correct answer is option 'A'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A cylindrical elastic body subjected to pure torsion about its axis d...
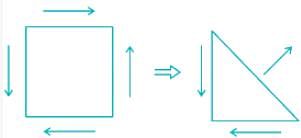
Pure torsion will be the case of pure shear in which principal normal stresses occur 45° to the axis.
Maximum and minimum principal stresses are equal in magnitude and opposite in direction.

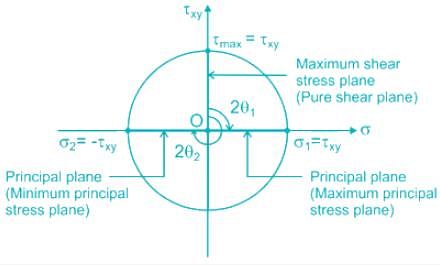
2θ1 = 90° ⇒ θ1 = 45°
Most Upvoted Answer
A cylindrical elastic body subjected to pure torsion about its axis d...
Tensile stress in a direction 45° to the axis:
When a cylindrical elastic body is subjected to pure torsion about its axis, the stress distribution within the body is different from other types of loading. In pure torsion, the stress is primarily shear stress and there are no axial or radial stresses.
In a cylindrical elastic body, the shear stress is directly proportional to the applied torque and inversely proportional to the polar moment of inertia. The shear stress can be calculated using the formula:
τ = T*r/J
Where:
τ = Shear stress
T = Applied torque
r = Radial distance from the axis of rotation
J = Polar moment of inertia
Since there are no axial or radial stresses in pure torsion, the only stress present is shear stress. The shear stress acts tangentially to the cross-section of the body and is maximum at the outer surface of the cylinder.
To find the direction of maximum tensile stress, we need to consider the Mohr's circle for shear stress. Mohr's circle is a graphical method used to determine principal stresses and their orientation.
In the case of pure torsion, the Mohr's circle for shear stress is a circle with its center at the origin and a radius equal to the maximum shear stress. The direction of the maximum tensile stress is given by a line passing through the center of the circle and making an angle of 45° with the axis of the cylinder.
Hence, the correct answer is option 'A' - Tensile stress in a direction 45° to the axis.
When a cylindrical elastic body is subjected to pure torsion about its axis, the stress distribution within the body is different from other types of loading. In pure torsion, the stress is primarily shear stress and there are no axial or radial stresses.
In a cylindrical elastic body, the shear stress is directly proportional to the applied torque and inversely proportional to the polar moment of inertia. The shear stress can be calculated using the formula:
τ = T*r/J
Where:
τ = Shear stress
T = Applied torque
r = Radial distance from the axis of rotation
J = Polar moment of inertia
Since there are no axial or radial stresses in pure torsion, the only stress present is shear stress. The shear stress acts tangentially to the cross-section of the body and is maximum at the outer surface of the cylinder.
To find the direction of maximum tensile stress, we need to consider the Mohr's circle for shear stress. Mohr's circle is a graphical method used to determine principal stresses and their orientation.
In the case of pure torsion, the Mohr's circle for shear stress is a circle with its center at the origin and a radius equal to the maximum shear stress. The direction of the maximum tensile stress is given by a line passing through the center of the circle and making an angle of 45° with the axis of the cylinder.
Hence, the correct answer is option 'A' - Tensile stress in a direction 45° to the axis.

|
Explore Courses for SSC exam
|

|
Similar SSC Doubts
A cylindrical elastic body subjected to pure torsion about its axis developsa)Tensile stress in a direction 45° to the axisb)No tensile or compressive stressc)Maximum shear stress along the axis of the shaftd)Maximum shear stress at 45° to the axisCorrect answer is option 'A'. Can you explain this answer?
Question Description
A cylindrical elastic body subjected to pure torsion about its axis developsa)Tensile stress in a direction 45° to the axisb)No tensile or compressive stressc)Maximum shear stress along the axis of the shaftd)Maximum shear stress at 45° to the axisCorrect answer is option 'A'. Can you explain this answer? for SSC 2024 is part of SSC preparation. The Question and answers have been prepared according to the SSC exam syllabus. Information about A cylindrical elastic body subjected to pure torsion about its axis developsa)Tensile stress in a direction 45° to the axisb)No tensile or compressive stressc)Maximum shear stress along the axis of the shaftd)Maximum shear stress at 45° to the axisCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for SSC 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A cylindrical elastic body subjected to pure torsion about its axis developsa)Tensile stress in a direction 45° to the axisb)No tensile or compressive stressc)Maximum shear stress along the axis of the shaftd)Maximum shear stress at 45° to the axisCorrect answer is option 'A'. Can you explain this answer?.
A cylindrical elastic body subjected to pure torsion about its axis developsa)Tensile stress in a direction 45° to the axisb)No tensile or compressive stressc)Maximum shear stress along the axis of the shaftd)Maximum shear stress at 45° to the axisCorrect answer is option 'A'. Can you explain this answer? for SSC 2024 is part of SSC preparation. The Question and answers have been prepared according to the SSC exam syllabus. Information about A cylindrical elastic body subjected to pure torsion about its axis developsa)Tensile stress in a direction 45° to the axisb)No tensile or compressive stressc)Maximum shear stress along the axis of the shaftd)Maximum shear stress at 45° to the axisCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for SSC 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A cylindrical elastic body subjected to pure torsion about its axis developsa)Tensile stress in a direction 45° to the axisb)No tensile or compressive stressc)Maximum shear stress along the axis of the shaftd)Maximum shear stress at 45° to the axisCorrect answer is option 'A'. Can you explain this answer?.
Solutions for A cylindrical elastic body subjected to pure torsion about its axis developsa)Tensile stress in a direction 45° to the axisb)No tensile or compressive stressc)Maximum shear stress along the axis of the shaftd)Maximum shear stress at 45° to the axisCorrect answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for SSC.
Download more important topics, notes, lectures and mock test series for SSC Exam by signing up for free.
Here you can find the meaning of A cylindrical elastic body subjected to pure torsion about its axis developsa)Tensile stress in a direction 45° to the axisb)No tensile or compressive stressc)Maximum shear stress along the axis of the shaftd)Maximum shear stress at 45° to the axisCorrect answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A cylindrical elastic body subjected to pure torsion about its axis developsa)Tensile stress in a direction 45° to the axisb)No tensile or compressive stressc)Maximum shear stress along the axis of the shaftd)Maximum shear stress at 45° to the axisCorrect answer is option 'A'. Can you explain this answer?, a detailed solution for A cylindrical elastic body subjected to pure torsion about its axis developsa)Tensile stress in a direction 45° to the axisb)No tensile or compressive stressc)Maximum shear stress along the axis of the shaftd)Maximum shear stress at 45° to the axisCorrect answer is option 'A'. Can you explain this answer? has been provided alongside types of A cylindrical elastic body subjected to pure torsion about its axis developsa)Tensile stress in a direction 45° to the axisb)No tensile or compressive stressc)Maximum shear stress along the axis of the shaftd)Maximum shear stress at 45° to the axisCorrect answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A cylindrical elastic body subjected to pure torsion about its axis developsa)Tensile stress in a direction 45° to the axisb)No tensile or compressive stressc)Maximum shear stress along the axis of the shaftd)Maximum shear stress at 45° to the axisCorrect answer is option 'A'. Can you explain this answer? tests, examples and also practice SSC tests.

|
Explore Courses for SSC exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















