SSC Exam > SSC Questions > The solid P floats with half its volume imme...
Start Learning for Free
The solid P floats with half its volume immersed in water, and the solid Q floats with one-third of its volume above the water surface. The densities of solid P and Q are in the ratio
- a)1: 3
- b)2: 3
- c)3: 4
- d)1: 2
Correct answer is option 'C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
The solid P floats with half its volume immersed in water, and the so...
When a body is either wholly or partially immersed in a fluid, a lift is generated due to the net vertical component of hydrostatic pressure forces experienced by the body. This lift is called the buoyant force, and the phenomenon is called buoyancy.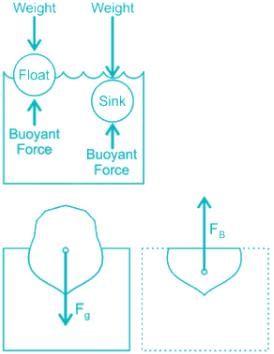
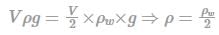
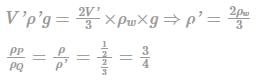
View all questions of this test
The Archimedes principle states that the buoyant force on a submerged body is equal to the weight of the liquid displaced by the body and acts vertically upward through the centroid of the displaced volume.
Thus, the net weight of the submerged body (the net vertical downward force experienced by it) is reduced from its actual weight by an amount that equals the buoyant force.
FB = ρghA = ρgV
FB = f(Vdisplaced, ρ)

Body P:
Volume = V, Density = ρ
Volume displaced = V/2
For floating body: Weight = Buoyant force
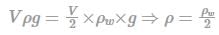
Body Q:
Volume = V', Density = ρ'
Volume displaced = V' - V'/3 = 2V'/3
For floating body: Weight = Buoyant force
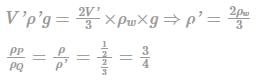
Most Upvoted Answer
The solid P floats with half its volume immersed in water, and the so...
Given:
- Solid P floats with half its volume immersed in water.
- Solid Q floats with one-third of its volume above the water surface.
To find:
The ratio of the densities of solid P and Q.
Explanation:
Let's assume the volume of solid P is Vp and its density is Dp. Similarly, let's assume the volume of solid Q is Vq and its density is Dq.
For solid P:
- Solid P floats with half its volume immersed in water. This means that the buoyant force acting on solid P is equal to the weight of the water displaced by half the volume of solid P.
- The buoyant force is given by the formula Buoyant force = Volume of fluid displaced × Density of fluid × g, where g is the acceleration due to gravity.
- Since solid P floats, the buoyant force is equal to the weight of solid P.
- Therefore, the weight of solid P is equal to the volume of water displaced by half the volume of solid P multiplied by the density of water and the acceleration due to gravity.
- Mathematically, we can write this as Vp × Dp × g = (Vp/2) × Dw × g, where Dw is the density of water.
- Simplifying this equation, we get Dp = (Dw/2).
For solid Q:
- Solid Q floats with one-third of its volume above the water surface. This means that the buoyant force acting on solid Q is equal to the weight of the water displaced by one-third of the volume of solid Q.
- Using similar logic as above, we can write the equation as Vq × Dq × g = (Vq/3) × Dw × g.
- Simplifying this equation, we get Dq = (Dw/3).
Ratio of densities:
- We need to find the ratio of Dp to Dq.
- Substituting the values of Dp and Dq from the above equations, we get Dp/Dq = (Dw/2)/(Dw/3).
- Simplifying this equation, we get Dp/Dq = 3/2.
- Therefore, the ratio of the densities of solid P and Q is 3:2.
Conclusion:
The correct answer is option 'C' - 3:2. The densities of solid P and Q are in the ratio of 3:2.
- Solid P floats with half its volume immersed in water.
- Solid Q floats with one-third of its volume above the water surface.
To find:
The ratio of the densities of solid P and Q.
Explanation:
Let's assume the volume of solid P is Vp and its density is Dp. Similarly, let's assume the volume of solid Q is Vq and its density is Dq.
For solid P:
- Solid P floats with half its volume immersed in water. This means that the buoyant force acting on solid P is equal to the weight of the water displaced by half the volume of solid P.
- The buoyant force is given by the formula Buoyant force = Volume of fluid displaced × Density of fluid × g, where g is the acceleration due to gravity.
- Since solid P floats, the buoyant force is equal to the weight of solid P.
- Therefore, the weight of solid P is equal to the volume of water displaced by half the volume of solid P multiplied by the density of water and the acceleration due to gravity.
- Mathematically, we can write this as Vp × Dp × g = (Vp/2) × Dw × g, where Dw is the density of water.
- Simplifying this equation, we get Dp = (Dw/2).
For solid Q:
- Solid Q floats with one-third of its volume above the water surface. This means that the buoyant force acting on solid Q is equal to the weight of the water displaced by one-third of the volume of solid Q.
- Using similar logic as above, we can write the equation as Vq × Dq × g = (Vq/3) × Dw × g.
- Simplifying this equation, we get Dq = (Dw/3).
Ratio of densities:
- We need to find the ratio of Dp to Dq.
- Substituting the values of Dp and Dq from the above equations, we get Dp/Dq = (Dw/2)/(Dw/3).
- Simplifying this equation, we get Dp/Dq = 3/2.
- Therefore, the ratio of the densities of solid P and Q is 3:2.
Conclusion:
The correct answer is option 'C' - 3:2. The densities of solid P and Q are in the ratio of 3:2.

|
Explore Courses for SSC exam
|

|
Similar SSC Doubts
The solid P floats with half its volume immersed in water, and the solid Q floats with one-third of its volume above the water surface. The densities of solid P and Q are in the ratioa)1: 3b)2: 3c)3: 4d)1: 2Correct answer is option 'C'. Can you explain this answer?
Question Description
The solid P floats with half its volume immersed in water, and the solid Q floats with one-third of its volume above the water surface. The densities of solid P and Q are in the ratioa)1: 3b)2: 3c)3: 4d)1: 2Correct answer is option 'C'. Can you explain this answer? for SSC 2024 is part of SSC preparation. The Question and answers have been prepared according to the SSC exam syllabus. Information about The solid P floats with half its volume immersed in water, and the solid Q floats with one-third of its volume above the water surface. The densities of solid P and Q are in the ratioa)1: 3b)2: 3c)3: 4d)1: 2Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for SSC 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The solid P floats with half its volume immersed in water, and the solid Q floats with one-third of its volume above the water surface. The densities of solid P and Q are in the ratioa)1: 3b)2: 3c)3: 4d)1: 2Correct answer is option 'C'. Can you explain this answer?.
The solid P floats with half its volume immersed in water, and the solid Q floats with one-third of its volume above the water surface. The densities of solid P and Q are in the ratioa)1: 3b)2: 3c)3: 4d)1: 2Correct answer is option 'C'. Can you explain this answer? for SSC 2024 is part of SSC preparation. The Question and answers have been prepared according to the SSC exam syllabus. Information about The solid P floats with half its volume immersed in water, and the solid Q floats with one-third of its volume above the water surface. The densities of solid P and Q are in the ratioa)1: 3b)2: 3c)3: 4d)1: 2Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for SSC 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The solid P floats with half its volume immersed in water, and the solid Q floats with one-third of its volume above the water surface. The densities of solid P and Q are in the ratioa)1: 3b)2: 3c)3: 4d)1: 2Correct answer is option 'C'. Can you explain this answer?.
Solutions for The solid P floats with half its volume immersed in water, and the solid Q floats with one-third of its volume above the water surface. The densities of solid P and Q are in the ratioa)1: 3b)2: 3c)3: 4d)1: 2Correct answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for SSC.
Download more important topics, notes, lectures and mock test series for SSC Exam by signing up for free.
Here you can find the meaning of The solid P floats with half its volume immersed in water, and the solid Q floats with one-third of its volume above the water surface. The densities of solid P and Q are in the ratioa)1: 3b)2: 3c)3: 4d)1: 2Correct answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
The solid P floats with half its volume immersed in water, and the solid Q floats with one-third of its volume above the water surface. The densities of solid P and Q are in the ratioa)1: 3b)2: 3c)3: 4d)1: 2Correct answer is option 'C'. Can you explain this answer?, a detailed solution for The solid P floats with half its volume immersed in water, and the solid Q floats with one-third of its volume above the water surface. The densities of solid P and Q are in the ratioa)1: 3b)2: 3c)3: 4d)1: 2Correct answer is option 'C'. Can you explain this answer? has been provided alongside types of The solid P floats with half its volume immersed in water, and the solid Q floats with one-third of its volume above the water surface. The densities of solid P and Q are in the ratioa)1: 3b)2: 3c)3: 4d)1: 2Correct answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice The solid P floats with half its volume immersed in water, and the solid Q floats with one-third of its volume above the water surface. The densities of solid P and Q are in the ratioa)1: 3b)2: 3c)3: 4d)1: 2Correct answer is option 'C'. Can you explain this answer? tests, examples and also practice SSC tests.

|
Explore Courses for SSC exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















