SSC Exam > SSC Questions > A certain R-L series combination is connecte...
Start Learning for Free
A certain R-L series combination is connected across a 50 Hz single-phase ac supply. If the instantaneous power drawn was found to be negative for 2 milliseconds in one cycle. The power factor angle of the circuit must be____
- a)9°
- b)18°
- c)36°
- d)45°
Correct answer is option 'C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A certain R-L series combination is connected across a 50 Hz single-p...
RL series circuit is an inductive circuit. Voltage leads the current. The instantaneous voltage and current can then be expressed as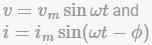

View all questions of this test
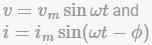
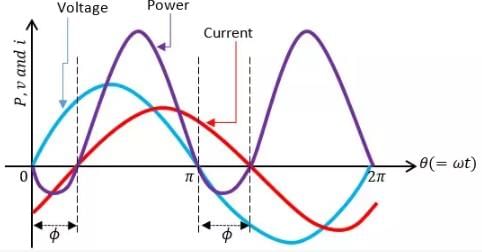
The instantaneous power can be obtained by multiplying the two. P =vi.

It can be seen from the diagram that in the angle interval 0 to ϕ, the voltage is positive but the current is negative and hence the power is negative. Similarly, in the angle interval π to π+ϕ the voltage is negative but the current is positive and hence the power is again negative.
In other regions the power is positive. Now we just have to find what time interval corresponds to phase difference ϕ. For this we use the formula,

Most Upvoted Answer
A certain R-L series combination is connected across a 50 Hz single-p...
Explanation:
Negative power indicates that the power is being returned to the source instead of being consumed by the load. This happens when the load is inductive, i.e., the current lags behind the voltage.
The power factor angle is the angle between the voltage and current phasors in an ac circuit. It is given by:
cos φ = P / (VI)
where φ is the power factor angle, P is the active power, V is the voltage, and I is the current.
Since the power is negative for 2 milliseconds in one cycle, the load is returning power to the source during that period. This means that the current is lagging behind the voltage, and the power factor angle is greater than 0°.
To find the power factor angle, we need to know the time delay between the voltage and current waveforms. This can be done by measuring the phase shift between the voltage and current using an oscilloscope or a power analyzer.
Assuming that the load is purely resistive for the rest of the cycle, the average power over one cycle should be zero. Therefore, the negative power during the 2 milliseconds should be compensated by positive power during the remaining time.
Let us assume that the load has an impedance Z = R + jX, where R is the resistance and X is the reactance. The power factor angle can be calculated as follows:
cos φ = (P1 - P2) / (Veff Ieff)
where P1 is the active power during the positive phase, P2 is the active power during the negative phase, Veff is the effective voltage, and Ieff is the effective current.
Since the load is purely resistive during the positive phase, P1 = VI cos φ1, where φ1 is the power factor angle during the positive phase. Therefore, cos φ1 = P1 / (VI).
During the negative phase, the power is negative, and the load is returning power to the source. Therefore, P2 = -VI cos φ2, where φ2 is the power factor angle during the negative phase. Therefore, cos φ2 = -P2 / (VI).
Since the average power over one cycle is zero, we have:
(P1 - P2) / 2 = 0
Therefore, P1 = P2 = P/2, where P is the active power over one cycle.
Substituting the values of P1 and P2, we get:
cos φ = P / (2Veff Ieff)
= -P / (2Veff Ieff) (since P2 is negative)
= -cos φ2 / 2
Therefore, cos φ2 = -2 cos φ
Since the power factor angle is greater than 0°, cos φ2 is negative. Therefore, cos φ must be positive, and the power factor angle must be between 0° and 90°.
The options given are:
a)9°
b)18°
c)36°
d)45°
The correct answer is option 'C', 36°, since it lies in the range of 0° to 90°.
Negative power indicates that the power is being returned to the source instead of being consumed by the load. This happens when the load is inductive, i.e., the current lags behind the voltage.
The power factor angle is the angle between the voltage and current phasors in an ac circuit. It is given by:
cos φ = P / (VI)
where φ is the power factor angle, P is the active power, V is the voltage, and I is the current.
Since the power is negative for 2 milliseconds in one cycle, the load is returning power to the source during that period. This means that the current is lagging behind the voltage, and the power factor angle is greater than 0°.
To find the power factor angle, we need to know the time delay between the voltage and current waveforms. This can be done by measuring the phase shift between the voltage and current using an oscilloscope or a power analyzer.
Assuming that the load is purely resistive for the rest of the cycle, the average power over one cycle should be zero. Therefore, the negative power during the 2 milliseconds should be compensated by positive power during the remaining time.
Let us assume that the load has an impedance Z = R + jX, where R is the resistance and X is the reactance. The power factor angle can be calculated as follows:
cos φ = (P1 - P2) / (Veff Ieff)
where P1 is the active power during the positive phase, P2 is the active power during the negative phase, Veff is the effective voltage, and Ieff is the effective current.
Since the load is purely resistive during the positive phase, P1 = VI cos φ1, where φ1 is the power factor angle during the positive phase. Therefore, cos φ1 = P1 / (VI).
During the negative phase, the power is negative, and the load is returning power to the source. Therefore, P2 = -VI cos φ2, where φ2 is the power factor angle during the negative phase. Therefore, cos φ2 = -P2 / (VI).
Since the average power over one cycle is zero, we have:
(P1 - P2) / 2 = 0
Therefore, P1 = P2 = P/2, where P is the active power over one cycle.
Substituting the values of P1 and P2, we get:
cos φ = P / (2Veff Ieff)
= -P / (2Veff Ieff) (since P2 is negative)
= -cos φ2 / 2
Therefore, cos φ2 = -2 cos φ
Since the power factor angle is greater than 0°, cos φ2 is negative. Therefore, cos φ must be positive, and the power factor angle must be between 0° and 90°.
The options given are:
a)9°
b)18°
c)36°
d)45°
The correct answer is option 'C', 36°, since it lies in the range of 0° to 90°.

|
Explore Courses for SSC exam
|

|
Similar SSC Doubts
A certain R-L series combination is connected across a 50 Hz single-phase ac supply. If the instantaneous power drawn was found to be negative for 2 milliseconds in one cycle. The power factor angle of the circuit must be____a)9°b)18°c)36°d)45°Correct answer is option 'C'. Can you explain this answer?
Question Description
A certain R-L series combination is connected across a 50 Hz single-phase ac supply. If the instantaneous power drawn was found to be negative for 2 milliseconds in one cycle. The power factor angle of the circuit must be____a)9°b)18°c)36°d)45°Correct answer is option 'C'. Can you explain this answer? for SSC 2024 is part of SSC preparation. The Question and answers have been prepared according to the SSC exam syllabus. Information about A certain R-L series combination is connected across a 50 Hz single-phase ac supply. If the instantaneous power drawn was found to be negative for 2 milliseconds in one cycle. The power factor angle of the circuit must be____a)9°b)18°c)36°d)45°Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for SSC 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A certain R-L series combination is connected across a 50 Hz single-phase ac supply. If the instantaneous power drawn was found to be negative for 2 milliseconds in one cycle. The power factor angle of the circuit must be____a)9°b)18°c)36°d)45°Correct answer is option 'C'. Can you explain this answer?.
A certain R-L series combination is connected across a 50 Hz single-phase ac supply. If the instantaneous power drawn was found to be negative for 2 milliseconds in one cycle. The power factor angle of the circuit must be____a)9°b)18°c)36°d)45°Correct answer is option 'C'. Can you explain this answer? for SSC 2024 is part of SSC preparation. The Question and answers have been prepared according to the SSC exam syllabus. Information about A certain R-L series combination is connected across a 50 Hz single-phase ac supply. If the instantaneous power drawn was found to be negative for 2 milliseconds in one cycle. The power factor angle of the circuit must be____a)9°b)18°c)36°d)45°Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for SSC 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A certain R-L series combination is connected across a 50 Hz single-phase ac supply. If the instantaneous power drawn was found to be negative for 2 milliseconds in one cycle. The power factor angle of the circuit must be____a)9°b)18°c)36°d)45°Correct answer is option 'C'. Can you explain this answer?.
Solutions for A certain R-L series combination is connected across a 50 Hz single-phase ac supply. If the instantaneous power drawn was found to be negative for 2 milliseconds in one cycle. The power factor angle of the circuit must be____a)9°b)18°c)36°d)45°Correct answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for SSC.
Download more important topics, notes, lectures and mock test series for SSC Exam by signing up for free.
Here you can find the meaning of A certain R-L series combination is connected across a 50 Hz single-phase ac supply. If the instantaneous power drawn was found to be negative for 2 milliseconds in one cycle. The power factor angle of the circuit must be____a)9°b)18°c)36°d)45°Correct answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A certain R-L series combination is connected across a 50 Hz single-phase ac supply. If the instantaneous power drawn was found to be negative for 2 milliseconds in one cycle. The power factor angle of the circuit must be____a)9°b)18°c)36°d)45°Correct answer is option 'C'. Can you explain this answer?, a detailed solution for A certain R-L series combination is connected across a 50 Hz single-phase ac supply. If the instantaneous power drawn was found to be negative for 2 milliseconds in one cycle. The power factor angle of the circuit must be____a)9°b)18°c)36°d)45°Correct answer is option 'C'. Can you explain this answer? has been provided alongside types of A certain R-L series combination is connected across a 50 Hz single-phase ac supply. If the instantaneous power drawn was found to be negative for 2 milliseconds in one cycle. The power factor angle of the circuit must be____a)9°b)18°c)36°d)45°Correct answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A certain R-L series combination is connected across a 50 Hz single-phase ac supply. If the instantaneous power drawn was found to be negative for 2 milliseconds in one cycle. The power factor angle of the circuit must be____a)9°b)18°c)36°d)45°Correct answer is option 'C'. Can you explain this answer? tests, examples and also practice SSC tests.

|
Explore Courses for SSC exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















