GATE Exam > GATE Questions > A galvanometer with internal resistance 100 ...
Start Learning for Free
A galvanometer with internal resistance 100 and full-scale current 1 mA is used to realize a dc voltmeter with a full-scale range of 1V. The full-scale range of this voltmeter can be extended to 10V by connecting an external resistance of value
- a)9k
- b)9.9k
- c)10k
- d)11k
Correct answer is option 'B'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A galvanometer with internal resistance 100 and full-scale current 1 ...
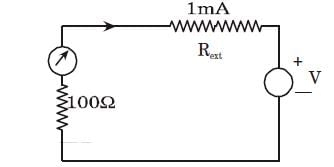
V = 10 = (100 + Rext ) 10– 3
Rext = 9.9 k
Most Upvoted Answer
A galvanometer with internal resistance 100 and full-scale current 1 ...
To extend the full-scale range of a galvanometer-based voltmeter, an external resistance needs to be connected in series with the galvanometer. Let's understand the process step by step:
1. Galvanometer:
A galvanometer is a device used to measure small currents. It consists of a coil of wire suspended in a magnetic field. When a current flows through the coil, it experiences a torque due to the interaction with the magnetic field, causing the coil to rotate.
2. Internal Resistance:
The galvanometer has an internal resistance, denoted as Rg. This resistance is in series with the coil and affects the measurement accuracy. In this case, the internal resistance is given as 100Ω.
3. Full-Scale Current:
The full-scale current of the galvanometer, denoted as Ig, is the maximum current that can flow through the coil without causing any damage. In this case, the full-scale current is given as 1mA.
4. Voltmeter Operation:
To convert the galvanometer into a voltmeter, an external resistance, denoted as Re, is connected in series with the galvanometer. The voltage to be measured is applied across the combination of the galvanometer and the external resistance.
5. Full-Scale Range:
The full-scale range of the voltmeter is the maximum voltage that can be measured without causing any damage to the galvanometer. In this case, the full-scale range of the voltmeter is given as 1V.
6. Calculating External Resistance:
To calculate the value of the external resistance required to extend the full-scale range to 10V, we can use the formula:
Vg = Ig(Rg + Re)
where Vg is the full-scale voltage of the voltmeter (1V) and Ig is the full-scale current of the galvanometer (1mA).
Plugging in the values, we get:
1V = (1mA)(100Ω + Re)
Rearranging the equation, we find:
Re = (1V - 1mA * 100Ω) / 1mA
Simplifying the equation, we get:
Re = (1V - 0.1V) / 0.001A
Re = 0.9V / 0.001A
Re = 900Ω
Hence, the correct answer is option B) 9.9kΩ, which is equal to 9900Ω.
1. Galvanometer:
A galvanometer is a device used to measure small currents. It consists of a coil of wire suspended in a magnetic field. When a current flows through the coil, it experiences a torque due to the interaction with the magnetic field, causing the coil to rotate.
2. Internal Resistance:
The galvanometer has an internal resistance, denoted as Rg. This resistance is in series with the coil and affects the measurement accuracy. In this case, the internal resistance is given as 100Ω.
3. Full-Scale Current:
The full-scale current of the galvanometer, denoted as Ig, is the maximum current that can flow through the coil without causing any damage. In this case, the full-scale current is given as 1mA.
4. Voltmeter Operation:
To convert the galvanometer into a voltmeter, an external resistance, denoted as Re, is connected in series with the galvanometer. The voltage to be measured is applied across the combination of the galvanometer and the external resistance.
5. Full-Scale Range:
The full-scale range of the voltmeter is the maximum voltage that can be measured without causing any damage to the galvanometer. In this case, the full-scale range of the voltmeter is given as 1V.
6. Calculating External Resistance:
To calculate the value of the external resistance required to extend the full-scale range to 10V, we can use the formula:
Vg = Ig(Rg + Re)
where Vg is the full-scale voltage of the voltmeter (1V) and Ig is the full-scale current of the galvanometer (1mA).
Plugging in the values, we get:
1V = (1mA)(100Ω + Re)
Rearranging the equation, we find:
Re = (1V - 1mA * 100Ω) / 1mA
Simplifying the equation, we get:
Re = (1V - 0.1V) / 0.001A
Re = 0.9V / 0.001A
Re = 900Ω
Hence, the correct answer is option B) 9.9kΩ, which is equal to 9900Ω.

|
Explore Courses for GATE exam
|

|
Similar GATE Doubts
A galvanometer with internal resistance 100 and full-scale current 1 mA is used to realize a dc voltmeter with a full-scale range of 1V. The full-scale range of this voltmeter can be extended to 10V by connecting an external resistance of valuea)9kb)9.9kc)10kd)11kCorrect answer is option 'B'. Can you explain this answer?
Question Description
A galvanometer with internal resistance 100 and full-scale current 1 mA is used to realize a dc voltmeter with a full-scale range of 1V. The full-scale range of this voltmeter can be extended to 10V by connecting an external resistance of valuea)9kb)9.9kc)10kd)11kCorrect answer is option 'B'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about A galvanometer with internal resistance 100 and full-scale current 1 mA is used to realize a dc voltmeter with a full-scale range of 1V. The full-scale range of this voltmeter can be extended to 10V by connecting an external resistance of valuea)9kb)9.9kc)10kd)11kCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A galvanometer with internal resistance 100 and full-scale current 1 mA is used to realize a dc voltmeter with a full-scale range of 1V. The full-scale range of this voltmeter can be extended to 10V by connecting an external resistance of valuea)9kb)9.9kc)10kd)11kCorrect answer is option 'B'. Can you explain this answer?.
A galvanometer with internal resistance 100 and full-scale current 1 mA is used to realize a dc voltmeter with a full-scale range of 1V. The full-scale range of this voltmeter can be extended to 10V by connecting an external resistance of valuea)9kb)9.9kc)10kd)11kCorrect answer is option 'B'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about A galvanometer with internal resistance 100 and full-scale current 1 mA is used to realize a dc voltmeter with a full-scale range of 1V. The full-scale range of this voltmeter can be extended to 10V by connecting an external resistance of valuea)9kb)9.9kc)10kd)11kCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A galvanometer with internal resistance 100 and full-scale current 1 mA is used to realize a dc voltmeter with a full-scale range of 1V. The full-scale range of this voltmeter can be extended to 10V by connecting an external resistance of valuea)9kb)9.9kc)10kd)11kCorrect answer is option 'B'. Can you explain this answer?.
Solutions for A galvanometer with internal resistance 100 and full-scale current 1 mA is used to realize a dc voltmeter with a full-scale range of 1V. The full-scale range of this voltmeter can be extended to 10V by connecting an external resistance of valuea)9kb)9.9kc)10kd)11kCorrect answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for GATE.
Download more important topics, notes, lectures and mock test series for GATE Exam by signing up for free.
Here you can find the meaning of A galvanometer with internal resistance 100 and full-scale current 1 mA is used to realize a dc voltmeter with a full-scale range of 1V. The full-scale range of this voltmeter can be extended to 10V by connecting an external resistance of valuea)9kb)9.9kc)10kd)11kCorrect answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A galvanometer with internal resistance 100 and full-scale current 1 mA is used to realize a dc voltmeter with a full-scale range of 1V. The full-scale range of this voltmeter can be extended to 10V by connecting an external resistance of valuea)9kb)9.9kc)10kd)11kCorrect answer is option 'B'. Can you explain this answer?, a detailed solution for A galvanometer with internal resistance 100 and full-scale current 1 mA is used to realize a dc voltmeter with a full-scale range of 1V. The full-scale range of this voltmeter can be extended to 10V by connecting an external resistance of valuea)9kb)9.9kc)10kd)11kCorrect answer is option 'B'. Can you explain this answer? has been provided alongside types of A galvanometer with internal resistance 100 and full-scale current 1 mA is used to realize a dc voltmeter with a full-scale range of 1V. The full-scale range of this voltmeter can be extended to 10V by connecting an external resistance of valuea)9kb)9.9kc)10kd)11kCorrect answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A galvanometer with internal resistance 100 and full-scale current 1 mA is used to realize a dc voltmeter with a full-scale range of 1V. The full-scale range of this voltmeter can be extended to 10V by connecting an external resistance of valuea)9kb)9.9kc)10kd)11kCorrect answer is option 'B'. Can you explain this answer? tests, examples and also practice GATE tests.

|
Explore Courses for GATE exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















