SSC Exam > SSC Questions > In finding Reynold’s number, the characteris...
Start Learning for Free
In finding Reynold’s number, the characteristic length of a circular pipe of diameter d is taken as
- a)d
- b)2d
- c)5d
- d)10d
Correct answer is option ''. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
In finding Reynold’s number, the characteristic length of a circular ...
Reynold Number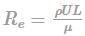
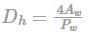
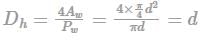
View all questions of this test
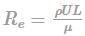
Where U is the average stream velocity, and L is the characteristics length/width.
The hydraulic diameter, which is used as the characteristic length in the determination of friction factor, instead of ordinary geometrical diameter, is defined as
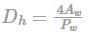
where Aw is the flow area and Pw is the wetted perimeter
Circular pipe of diameter d:
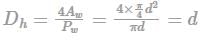
Most Upvoted Answer
In finding Reynold’s number, the characteristic length of a circular ...
In finding Reynolds number, the characteristic length of a circular pipe of diameter d is taken as 2d. This is because the Reynolds number is a dimensionless quantity that represents the ratio of inertial forces to viscous forces in a flowing fluid.
Understanding Reynolds Number:
Reynolds number (Re) is used to determine the flow regime of a fluid, whether it is laminar or turbulent. It is calculated using the formula:
Re = (ρ * v * L) / μ
where:
- ρ is the density of the fluid
- v is the velocity of the fluid
- L is the characteristic length of the flow
- μ is the dynamic viscosity of the fluid
Explanation of the Correct Answer:
The characteristic length (L) in the Reynolds number calculation is a measure of the size or scale of the flow geometry. For a circular pipe, the characteristic length can be defined in different ways, such as the pipe diameter (d), the hydraulic diameter (4 times the cross-sectional area divided by the wetted perimeter), or the pipe length.
In this case, the correct answer is option '2d'. This means that the characteristic length is taken as twice the diameter of the circular pipe. This choice is based on the fact that the diameter is a representative length scale for a pipe.
Reasoning behind Option '2d':
The reason for choosing the characteristic length as 2d can be understood by considering the flow behavior in a circular pipe. In laminar flow, the fluid flows in smooth, parallel layers with little mixing between them. In this case, the flow behavior is primarily determined by the pipe diameter itself. Hence, it makes sense to take the characteristic length as 2d, as it represents the size of the pipe.
On the other hand, in turbulent flow, the fluid undergoes chaotic motion with significant mixing and eddies. The flow behavior is influenced by factors such as the pipe roughness and length. However, even in turbulent flow, the pipe diameter still plays a significant role in determining the flow characteristics. Therefore, taking the characteristic length as 2d is a reasonable choice.
In conclusion, the characteristic length of a circular pipe of diameter d is taken as 2d when calculating the Reynolds number because the diameter is a representative length scale for the pipe, and it influences the flow behavior in both laminar and turbulent flow regimes.
Understanding Reynolds Number:
Reynolds number (Re) is used to determine the flow regime of a fluid, whether it is laminar or turbulent. It is calculated using the formula:
Re = (ρ * v * L) / μ
where:
- ρ is the density of the fluid
- v is the velocity of the fluid
- L is the characteristic length of the flow
- μ is the dynamic viscosity of the fluid
Explanation of the Correct Answer:
The characteristic length (L) in the Reynolds number calculation is a measure of the size or scale of the flow geometry. For a circular pipe, the characteristic length can be defined in different ways, such as the pipe diameter (d), the hydraulic diameter (4 times the cross-sectional area divided by the wetted perimeter), or the pipe length.
In this case, the correct answer is option '2d'. This means that the characteristic length is taken as twice the diameter of the circular pipe. This choice is based on the fact that the diameter is a representative length scale for a pipe.
Reasoning behind Option '2d':
The reason for choosing the characteristic length as 2d can be understood by considering the flow behavior in a circular pipe. In laminar flow, the fluid flows in smooth, parallel layers with little mixing between them. In this case, the flow behavior is primarily determined by the pipe diameter itself. Hence, it makes sense to take the characteristic length as 2d, as it represents the size of the pipe.
On the other hand, in turbulent flow, the fluid undergoes chaotic motion with significant mixing and eddies. The flow behavior is influenced by factors such as the pipe roughness and length. However, even in turbulent flow, the pipe diameter still plays a significant role in determining the flow characteristics. Therefore, taking the characteristic length as 2d is a reasonable choice.
In conclusion, the characteristic length of a circular pipe of diameter d is taken as 2d when calculating the Reynolds number because the diameter is a representative length scale for the pipe, and it influences the flow behavior in both laminar and turbulent flow regimes.

|
Explore Courses for SSC exam
|

|
Similar SSC Doubts
In finding Reynold’s number, the characteristic length of a circular pipe of diameter d is taken asa)db)2dc)5dd)10dCorrect answer is option ''. Can you explain this answer?
Question Description
In finding Reynold’s number, the characteristic length of a circular pipe of diameter d is taken asa)db)2dc)5dd)10dCorrect answer is option ''. Can you explain this answer? for SSC 2024 is part of SSC preparation. The Question and answers have been prepared according to the SSC exam syllabus. Information about In finding Reynold’s number, the characteristic length of a circular pipe of diameter d is taken asa)db)2dc)5dd)10dCorrect answer is option ''. Can you explain this answer? covers all topics & solutions for SSC 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for In finding Reynold’s number, the characteristic length of a circular pipe of diameter d is taken asa)db)2dc)5dd)10dCorrect answer is option ''. Can you explain this answer?.
In finding Reynold’s number, the characteristic length of a circular pipe of diameter d is taken asa)db)2dc)5dd)10dCorrect answer is option ''. Can you explain this answer? for SSC 2024 is part of SSC preparation. The Question and answers have been prepared according to the SSC exam syllabus. Information about In finding Reynold’s number, the characteristic length of a circular pipe of diameter d is taken asa)db)2dc)5dd)10dCorrect answer is option ''. Can you explain this answer? covers all topics & solutions for SSC 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for In finding Reynold’s number, the characteristic length of a circular pipe of diameter d is taken asa)db)2dc)5dd)10dCorrect answer is option ''. Can you explain this answer?.
Solutions for In finding Reynold’s number, the characteristic length of a circular pipe of diameter d is taken asa)db)2dc)5dd)10dCorrect answer is option ''. Can you explain this answer? in English & in Hindi are available as part of our courses for SSC.
Download more important topics, notes, lectures and mock test series for SSC Exam by signing up for free.
Here you can find the meaning of In finding Reynold’s number, the characteristic length of a circular pipe of diameter d is taken asa)db)2dc)5dd)10dCorrect answer is option ''. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
In finding Reynold’s number, the characteristic length of a circular pipe of diameter d is taken asa)db)2dc)5dd)10dCorrect answer is option ''. Can you explain this answer?, a detailed solution for In finding Reynold’s number, the characteristic length of a circular pipe of diameter d is taken asa)db)2dc)5dd)10dCorrect answer is option ''. Can you explain this answer? has been provided alongside types of In finding Reynold’s number, the characteristic length of a circular pipe of diameter d is taken asa)db)2dc)5dd)10dCorrect answer is option ''. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice In finding Reynold’s number, the characteristic length of a circular pipe of diameter d is taken asa)db)2dc)5dd)10dCorrect answer is option ''. Can you explain this answer? tests, examples and also practice SSC tests.

|
Explore Courses for SSC exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















