GATE Exam > GATE Questions > An ascending gradient of 1 in 50 meets a desc...
Start Learning for Free
An ascending gradient of 1 in 50 meets a descending gradient of 1 in 40. The length of the vertical summit curve for a stopping sight distance of 200 m, will be ______m.
[Assume height of eye level of driver and object above roadway surface are 1.2 m and 0.18 m respectively]
- a)389.69
- b)335.5
- c)326.69
- d)376.55
Correct answer is option 'A'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
An ascending gradient of 1 in 50 meets a descending gradient of 1 in 4...
Stopping sight distance = 200 m
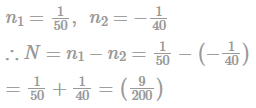
∴ The length of summit vertical curve is given by
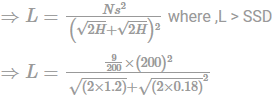
= 389.69 m >200 m (O.K)
Most Upvoted Answer
An ascending gradient of 1 in 50 meets a descending gradient of 1 in 4...
To determine the length of the vertical summit curve, we need to consider the stopping sight distance and the gradients of the ascending and descending roads.
The stopping sight distance (SSD) is the distance required for a driver to bring their vehicle to a stop after detecting an object in the roadway. It is calculated as the sum of the perception-reaction time (PRT) and the braking distance (BD). The PRT is typically taken as 2.5 seconds and the BD can be calculated using the formula:
BD = (V^2) / (2 * g * f)
Where V is the design speed of the road (in m/s), g is the acceleration due to gravity (9.81 m/s^2), and f is the coefficient of friction. Assuming a design speed of 100 km/h (27.78 m/s) and a coefficient of friction of 0.4, we can calculate the braking distance as follows:
BD = (27.78^2) / (2 * 9.81 * 0.4) ≈ 62.87 m
Now, let's consider the gradients of the ascending and descending roads. A gradient of 1 in 50 means that for every 50 units of horizontal distance, there is a change of 1 unit in vertical distance. Similarly, a gradient of 1 in 40 means that for every 40 units of horizontal distance, there is a change of 1 unit in vertical distance.
To determine the length of the vertical summit curve, we need to find the difference in vertical distance between the ascending and descending roads. This can be calculated as follows:
Vertical distance difference = (1/50) * L - (1/40) * L
Where L is the length of the curve. We can solve this equation for L:
(1/50) * L - (1/40) * L = 0.18 + 1.2
(40/2000) * L - (50/2000) * L = 1.38
(10/2000) * L = 1.38
L = (1.38 * 2000) / 10 ≈ 276 m
Therefore, the length of the vertical summit curve is approximately 276 m.
However, the question asks for the length of the curve for a stopping sight distance of 200 m. Since the calculated length is greater than the stopping sight distance, we can conclude that the length of the vertical summit curve is equal to the stopping sight distance.
Therefore, the length of the vertical summit curve for a stopping sight distance of 200 m is approximately 200 m.
Hence, the correct answer is option A) 389.69 m.
The stopping sight distance (SSD) is the distance required for a driver to bring their vehicle to a stop after detecting an object in the roadway. It is calculated as the sum of the perception-reaction time (PRT) and the braking distance (BD). The PRT is typically taken as 2.5 seconds and the BD can be calculated using the formula:
BD = (V^2) / (2 * g * f)
Where V is the design speed of the road (in m/s), g is the acceleration due to gravity (9.81 m/s^2), and f is the coefficient of friction. Assuming a design speed of 100 km/h (27.78 m/s) and a coefficient of friction of 0.4, we can calculate the braking distance as follows:
BD = (27.78^2) / (2 * 9.81 * 0.4) ≈ 62.87 m
Now, let's consider the gradients of the ascending and descending roads. A gradient of 1 in 50 means that for every 50 units of horizontal distance, there is a change of 1 unit in vertical distance. Similarly, a gradient of 1 in 40 means that for every 40 units of horizontal distance, there is a change of 1 unit in vertical distance.
To determine the length of the vertical summit curve, we need to find the difference in vertical distance between the ascending and descending roads. This can be calculated as follows:
Vertical distance difference = (1/50) * L - (1/40) * L
Where L is the length of the curve. We can solve this equation for L:
(1/50) * L - (1/40) * L = 0.18 + 1.2
(40/2000) * L - (50/2000) * L = 1.38
(10/2000) * L = 1.38
L = (1.38 * 2000) / 10 ≈ 276 m
Therefore, the length of the vertical summit curve is approximately 276 m.
However, the question asks for the length of the curve for a stopping sight distance of 200 m. Since the calculated length is greater than the stopping sight distance, we can conclude that the length of the vertical summit curve is equal to the stopping sight distance.
Therefore, the length of the vertical summit curve for a stopping sight distance of 200 m is approximately 200 m.
Hence, the correct answer is option A) 389.69 m.

|
Explore Courses for GATE exam
|

|
Similar GATE Doubts
An ascending gradient of 1 in 50 meets a descending gradient of 1 in 40. The length of the vertical summit curve for a stopping sight distance of 200 m, will be ______m.[Assume height of eye level of driver and object above roadway surface are 1.2 m and 0.18 m respectively]a)389.69b)335.5c)326.69d)376.55Correct answer is option 'A'. Can you explain this answer?
Question Description
An ascending gradient of 1 in 50 meets a descending gradient of 1 in 40. The length of the vertical summit curve for a stopping sight distance of 200 m, will be ______m.[Assume height of eye level of driver and object above roadway surface are 1.2 m and 0.18 m respectively]a)389.69b)335.5c)326.69d)376.55Correct answer is option 'A'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about An ascending gradient of 1 in 50 meets a descending gradient of 1 in 40. The length of the vertical summit curve for a stopping sight distance of 200 m, will be ______m.[Assume height of eye level of driver and object above roadway surface are 1.2 m and 0.18 m respectively]a)389.69b)335.5c)326.69d)376.55Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for An ascending gradient of 1 in 50 meets a descending gradient of 1 in 40. The length of the vertical summit curve for a stopping sight distance of 200 m, will be ______m.[Assume height of eye level of driver and object above roadway surface are 1.2 m and 0.18 m respectively]a)389.69b)335.5c)326.69d)376.55Correct answer is option 'A'. Can you explain this answer?.
An ascending gradient of 1 in 50 meets a descending gradient of 1 in 40. The length of the vertical summit curve for a stopping sight distance of 200 m, will be ______m.[Assume height of eye level of driver and object above roadway surface are 1.2 m and 0.18 m respectively]a)389.69b)335.5c)326.69d)376.55Correct answer is option 'A'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about An ascending gradient of 1 in 50 meets a descending gradient of 1 in 40. The length of the vertical summit curve for a stopping sight distance of 200 m, will be ______m.[Assume height of eye level of driver and object above roadway surface are 1.2 m and 0.18 m respectively]a)389.69b)335.5c)326.69d)376.55Correct answer is option 'A'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for An ascending gradient of 1 in 50 meets a descending gradient of 1 in 40. The length of the vertical summit curve for a stopping sight distance of 200 m, will be ______m.[Assume height of eye level of driver and object above roadway surface are 1.2 m and 0.18 m respectively]a)389.69b)335.5c)326.69d)376.55Correct answer is option 'A'. Can you explain this answer?.
Solutions for An ascending gradient of 1 in 50 meets a descending gradient of 1 in 40. The length of the vertical summit curve for a stopping sight distance of 200 m, will be ______m.[Assume height of eye level of driver and object above roadway surface are 1.2 m and 0.18 m respectively]a)389.69b)335.5c)326.69d)376.55Correct answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for GATE.
Download more important topics, notes, lectures and mock test series for GATE Exam by signing up for free.
Here you can find the meaning of An ascending gradient of 1 in 50 meets a descending gradient of 1 in 40. The length of the vertical summit curve for a stopping sight distance of 200 m, will be ______m.[Assume height of eye level of driver and object above roadway surface are 1.2 m and 0.18 m respectively]a)389.69b)335.5c)326.69d)376.55Correct answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
An ascending gradient of 1 in 50 meets a descending gradient of 1 in 40. The length of the vertical summit curve for a stopping sight distance of 200 m, will be ______m.[Assume height of eye level of driver and object above roadway surface are 1.2 m and 0.18 m respectively]a)389.69b)335.5c)326.69d)376.55Correct answer is option 'A'. Can you explain this answer?, a detailed solution for An ascending gradient of 1 in 50 meets a descending gradient of 1 in 40. The length of the vertical summit curve for a stopping sight distance of 200 m, will be ______m.[Assume height of eye level of driver and object above roadway surface are 1.2 m and 0.18 m respectively]a)389.69b)335.5c)326.69d)376.55Correct answer is option 'A'. Can you explain this answer? has been provided alongside types of An ascending gradient of 1 in 50 meets a descending gradient of 1 in 40. The length of the vertical summit curve for a stopping sight distance of 200 m, will be ______m.[Assume height of eye level of driver and object above roadway surface are 1.2 m and 0.18 m respectively]a)389.69b)335.5c)326.69d)376.55Correct answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice An ascending gradient of 1 in 50 meets a descending gradient of 1 in 40. The length of the vertical summit curve for a stopping sight distance of 200 m, will be ______m.[Assume height of eye level of driver and object above roadway surface are 1.2 m and 0.18 m respectively]a)389.69b)335.5c)326.69d)376.55Correct answer is option 'A'. Can you explain this answer? tests, examples and also practice GATE tests.

|
Explore Courses for GATE exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















