GATE Exam > GATE Questions > A laboratory model of a river is built to a ...
Start Learning for Free
A laboratory model of a river is built to a geometric scale of 1:200. The fluid used in the model is oil of mass density 850 kg/m3. The highest flood in the river is 12000 m3/s. the corresponding discharge in the model shall be
- a)0.021 m3/s
- b)0.101 m3/s
- c)0.278 m3/s
- d)4.25 m3/s
Correct answer is option 'A'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A laboratory model of a river is built to a geometric scale of 1:200....
Scale ratio, Lr = 1/200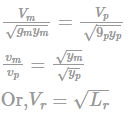
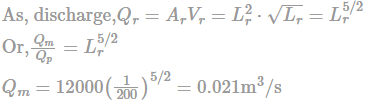
View all questions of this test
Flow in river is based on gravitational force. So, model will be based on Froude number.
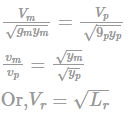
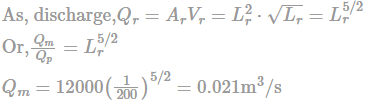
Most Upvoted Answer
A laboratory model of a river is built to a geometric scale of 1:200....
To find the corresponding discharge in the model, we need to use the geometric scale and the mass density of the fluid.
Geometric Scale:
The geometric scale of 1:200 means that every dimension in the model is 200 times smaller than the corresponding dimension in the actual river. This includes both the length and the cross-sectional area.
Mass Density:
The mass density of the oil used in the model is given as 850 kg/m^3. This means that for every cubic meter of oil, there is a mass of 850 kg.
Finding the Corresponding Discharge:
The discharge of the river is given as 12000 m^3/s. We need to find the corresponding discharge in the model.
Since the cross-sectional area is also scaled down by a factor of 200, the discharge in the model will also be scaled down by the same factor.
Let's denote the corresponding discharge in the model as Qm. We can set up the following equation:
Qm = Qa / S
where Qa is the actual discharge in the river and S is the scale factor (200 in this case).
Substituting the given values, we have:
Qm = 12000 m^3/s / 200
Qm = 60 m^3/s
However, we need to consider the mass density of the fluid as well. Since the mass density of the oil used in the model is 850 kg/m^3, we need to convert the discharge from cubic meters to cubic meters of oil.
To do this, we multiply the discharge in cubic meters by the mass density:
Qm = 60 m^3/s * 850 kg/m^3
Qm = 51000 kg/s
Finally, we convert the discharge from kilograms per second to cubic meters per second by dividing by the mass density:
Qm = 51000 kg/s / 850 kg/m^3
Qm = 60 m^3/s
The corresponding discharge in the model is 0.021 m^3/s.
Therefore, the correct answer is option A) 0.021 m^3/s.
Geometric Scale:
The geometric scale of 1:200 means that every dimension in the model is 200 times smaller than the corresponding dimension in the actual river. This includes both the length and the cross-sectional area.
Mass Density:
The mass density of the oil used in the model is given as 850 kg/m^3. This means that for every cubic meter of oil, there is a mass of 850 kg.
Finding the Corresponding Discharge:
The discharge of the river is given as 12000 m^3/s. We need to find the corresponding discharge in the model.
Since the cross-sectional area is also scaled down by a factor of 200, the discharge in the model will also be scaled down by the same factor.
Let's denote the corresponding discharge in the model as Qm. We can set up the following equation:
Qm = Qa / S
where Qa is the actual discharge in the river and S is the scale factor (200 in this case).
Substituting the given values, we have:
Qm = 12000 m^3/s / 200
Qm = 60 m^3/s
However, we need to consider the mass density of the fluid as well. Since the mass density of the oil used in the model is 850 kg/m^3, we need to convert the discharge from cubic meters to cubic meters of oil.
To do this, we multiply the discharge in cubic meters by the mass density:
Qm = 60 m^3/s * 850 kg/m^3
Qm = 51000 kg/s
Finally, we convert the discharge from kilograms per second to cubic meters per second by dividing by the mass density:
Qm = 51000 kg/s / 850 kg/m^3
Qm = 60 m^3/s
The corresponding discharge in the model is 0.021 m^3/s.
Therefore, the correct answer is option A) 0.021 m^3/s.

|
Explore Courses for GATE exam
|

|
Similar GATE Doubts
A laboratory model of a river is built to a geometric scale of 1:200. The fluid used in the model is oil of mass density 850 kg/m3. The highest flood in the river is 12000 m3/s. the corresponding discharge in the model shall bea)0.021 m3/sb)0.101 m3/sc)0.278 m3/sd)4.25 m3/sCorrect answer is option 'A'. Can you explain this answer?
Question Description
A laboratory model of a river is built to a geometric scale of 1:200. The fluid used in the model is oil of mass density 850 kg/m3. The highest flood in the river is 12000 m3/s. the corresponding discharge in the model shall bea)0.021 m3/sb)0.101 m3/sc)0.278 m3/sd)4.25 m3/sCorrect answer is option 'A'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about A laboratory model of a river is built to a geometric scale of 1:200. The fluid used in the model is oil of mass density 850 kg/m3. The highest flood in the river is 12000 m3/s. the corresponding discharge in the model shall bea)0.021 m3/sb)0.101 m3/sc)0.278 m3/sd)4.25 m3/sCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A laboratory model of a river is built to a geometric scale of 1:200. The fluid used in the model is oil of mass density 850 kg/m3. The highest flood in the river is 12000 m3/s. the corresponding discharge in the model shall bea)0.021 m3/sb)0.101 m3/sc)0.278 m3/sd)4.25 m3/sCorrect answer is option 'A'. Can you explain this answer?.
A laboratory model of a river is built to a geometric scale of 1:200. The fluid used in the model is oil of mass density 850 kg/m3. The highest flood in the river is 12000 m3/s. the corresponding discharge in the model shall bea)0.021 m3/sb)0.101 m3/sc)0.278 m3/sd)4.25 m3/sCorrect answer is option 'A'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about A laboratory model of a river is built to a geometric scale of 1:200. The fluid used in the model is oil of mass density 850 kg/m3. The highest flood in the river is 12000 m3/s. the corresponding discharge in the model shall bea)0.021 m3/sb)0.101 m3/sc)0.278 m3/sd)4.25 m3/sCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A laboratory model of a river is built to a geometric scale of 1:200. The fluid used in the model is oil of mass density 850 kg/m3. The highest flood in the river is 12000 m3/s. the corresponding discharge in the model shall bea)0.021 m3/sb)0.101 m3/sc)0.278 m3/sd)4.25 m3/sCorrect answer is option 'A'. Can you explain this answer?.
Solutions for A laboratory model of a river is built to a geometric scale of 1:200. The fluid used in the model is oil of mass density 850 kg/m3. The highest flood in the river is 12000 m3/s. the corresponding discharge in the model shall bea)0.021 m3/sb)0.101 m3/sc)0.278 m3/sd)4.25 m3/sCorrect answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for GATE.
Download more important topics, notes, lectures and mock test series for GATE Exam by signing up for free.
Here you can find the meaning of A laboratory model of a river is built to a geometric scale of 1:200. The fluid used in the model is oil of mass density 850 kg/m3. The highest flood in the river is 12000 m3/s. the corresponding discharge in the model shall bea)0.021 m3/sb)0.101 m3/sc)0.278 m3/sd)4.25 m3/sCorrect answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A laboratory model of a river is built to a geometric scale of 1:200. The fluid used in the model is oil of mass density 850 kg/m3. The highest flood in the river is 12000 m3/s. the corresponding discharge in the model shall bea)0.021 m3/sb)0.101 m3/sc)0.278 m3/sd)4.25 m3/sCorrect answer is option 'A'. Can you explain this answer?, a detailed solution for A laboratory model of a river is built to a geometric scale of 1:200. The fluid used in the model is oil of mass density 850 kg/m3. The highest flood in the river is 12000 m3/s. the corresponding discharge in the model shall bea)0.021 m3/sb)0.101 m3/sc)0.278 m3/sd)4.25 m3/sCorrect answer is option 'A'. Can you explain this answer? has been provided alongside types of A laboratory model of a river is built to a geometric scale of 1:200. The fluid used in the model is oil of mass density 850 kg/m3. The highest flood in the river is 12000 m3/s. the corresponding discharge in the model shall bea)0.021 m3/sb)0.101 m3/sc)0.278 m3/sd)4.25 m3/sCorrect answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A laboratory model of a river is built to a geometric scale of 1:200. The fluid used in the model is oil of mass density 850 kg/m3. The highest flood in the river is 12000 m3/s. the corresponding discharge in the model shall bea)0.021 m3/sb)0.101 m3/sc)0.278 m3/sd)4.25 m3/sCorrect answer is option 'A'. Can you explain this answer? tests, examples and also practice GATE tests.

|
Explore Courses for GATE exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















