GATE Exam > GATE Questions > If two gears have moment of inertia as I1 an...
Start Learning for Free
If two gears have moment of inertia as I1 and I2 respectively and mesh with a speed ratio ω2/ω1 = n then equivalent moment of inertia of both gears referred to first one is?
- a)n2I1 + I2
- b)I1 + nI2
- c)nI1 + I2
- d)I1 + n2I2
Correct answer is option 'D'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
If two gears have moment of inertia as I1 and I2 respectively and mes...
Between shaft 1 and shaft 2 the kinetic energy will be same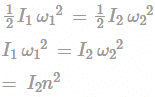
View all questions of this test
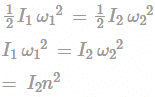
So equivalent moment of inertia w.r.t to first one = I1 + n2I2
Most Upvoted Answer
If two gears have moment of inertia as I1 and I2 respectively and mes...
Explanation:
When two gears mesh with each other, they transmit torque and rotate at different speeds. The speed ratio of the two gears is given by the equation:
ω2/ω1 = n
Where ω1 is the angular speed of the first gear and ω2 is the angular speed of the second gear.
The moment of inertia of an object is a measure of its resistance to changes in its rotational motion. It depends on the mass distribution of the object. The moment of inertia of the first gear is given by I1 and the moment of inertia of the second gear is given by I2.
When two gears mesh, the total moment of inertia of the system can be calculated by adding the individual moments of inertia of the gears. However, if we want to find the equivalent moment of inertia referred to the first gear, we need to take into account the speed ratio of the gears.
Equivalent Moment of Inertia:
To find the equivalent moment of inertia of the two gears referred to the first gear, we can use the following equation:
Ieq = I1 + (n^2) * I2
Where Ieq is the equivalent moment of inertia referred to the first gear, n is the speed ratio of the gears, I1 is the moment of inertia of the first gear, and I2 is the moment of inertia of the second gear.
Derivation:
Let's derive the above equation:
The angular speed ratio of the two gears is given by:
ω2/ω1 = n
We can rewrite this equation as:
ω2 = n * ω1
The kinetic energy of a rotating object is given by:
K = (1/2) * I * ω^2
Where K is the kinetic energy, I is the moment of inertia, and ω is the angular speed.
The kinetic energy of the first gear is given by:
K1 = (1/2) * I1 * ω1^2
The kinetic energy of the second gear is given by:
K2 = (1/2) * I2 * ω2^2
Substituting ω2 = n * ω1 into the equation for K2, we get:
K2 = (1/2) * I2 * (n * ω1)^2
= (1/2) * I2 * n^2 * ω1^2
The total kinetic energy of the system is given by:
Ktotal = K1 + K2
= (1/2) * I1 * ω1^2 + (1/2) * I2 * n^2 * ω1^2
= (1/2) * (I1 + n^2 * I2) * ω1^2
Comparing this equation with the equation for the kinetic energy of a rotating object, we can see that the moment of inertia of the system referred to the first gear is:
Ieq = I1 + (n^2) * I2
Therefore, the correct answer is option D: I1 + n^2 * I2.
When two gears mesh with each other, they transmit torque and rotate at different speeds. The speed ratio of the two gears is given by the equation:
ω2/ω1 = n
Where ω1 is the angular speed of the first gear and ω2 is the angular speed of the second gear.
The moment of inertia of an object is a measure of its resistance to changes in its rotational motion. It depends on the mass distribution of the object. The moment of inertia of the first gear is given by I1 and the moment of inertia of the second gear is given by I2.
When two gears mesh, the total moment of inertia of the system can be calculated by adding the individual moments of inertia of the gears. However, if we want to find the equivalent moment of inertia referred to the first gear, we need to take into account the speed ratio of the gears.
Equivalent Moment of Inertia:
To find the equivalent moment of inertia of the two gears referred to the first gear, we can use the following equation:
Ieq = I1 + (n^2) * I2
Where Ieq is the equivalent moment of inertia referred to the first gear, n is the speed ratio of the gears, I1 is the moment of inertia of the first gear, and I2 is the moment of inertia of the second gear.
Derivation:
Let's derive the above equation:
The angular speed ratio of the two gears is given by:
ω2/ω1 = n
We can rewrite this equation as:
ω2 = n * ω1
The kinetic energy of a rotating object is given by:
K = (1/2) * I * ω^2
Where K is the kinetic energy, I is the moment of inertia, and ω is the angular speed.
The kinetic energy of the first gear is given by:
K1 = (1/2) * I1 * ω1^2
The kinetic energy of the second gear is given by:
K2 = (1/2) * I2 * ω2^2
Substituting ω2 = n * ω1 into the equation for K2, we get:
K2 = (1/2) * I2 * (n * ω1)^2
= (1/2) * I2 * n^2 * ω1^2
The total kinetic energy of the system is given by:
Ktotal = K1 + K2
= (1/2) * I1 * ω1^2 + (1/2) * I2 * n^2 * ω1^2
= (1/2) * (I1 + n^2 * I2) * ω1^2
Comparing this equation with the equation for the kinetic energy of a rotating object, we can see that the moment of inertia of the system referred to the first gear is:
Ieq = I1 + (n^2) * I2
Therefore, the correct answer is option D: I1 + n^2 * I2.

|
Explore Courses for GATE exam
|

|
Similar GATE Doubts
If two gears have moment of inertia as I1 and I2 respectively and mesh with a speed ratio ω2/ω1 = n then equivalent moment of inertia of both gears referred to first one is?a)n2I1 + I2b)I1 + nI2c)nI1 + I2d)I1 + n2I2Correct answer is option 'D'. Can you explain this answer?
Question Description
If two gears have moment of inertia as I1 and I2 respectively and mesh with a speed ratio ω2/ω1 = n then equivalent moment of inertia of both gears referred to first one is?a)n2I1 + I2b)I1 + nI2c)nI1 + I2d)I1 + n2I2Correct answer is option 'D'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about If two gears have moment of inertia as I1 and I2 respectively and mesh with a speed ratio ω2/ω1 = n then equivalent moment of inertia of both gears referred to first one is?a)n2I1 + I2b)I1 + nI2c)nI1 + I2d)I1 + n2I2Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If two gears have moment of inertia as I1 and I2 respectively and mesh with a speed ratio ω2/ω1 = n then equivalent moment of inertia of both gears referred to first one is?a)n2I1 + I2b)I1 + nI2c)nI1 + I2d)I1 + n2I2Correct answer is option 'D'. Can you explain this answer?.
If two gears have moment of inertia as I1 and I2 respectively and mesh with a speed ratio ω2/ω1 = n then equivalent moment of inertia of both gears referred to first one is?a)n2I1 + I2b)I1 + nI2c)nI1 + I2d)I1 + n2I2Correct answer is option 'D'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about If two gears have moment of inertia as I1 and I2 respectively and mesh with a speed ratio ω2/ω1 = n then equivalent moment of inertia of both gears referred to first one is?a)n2I1 + I2b)I1 + nI2c)nI1 + I2d)I1 + n2I2Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for If two gears have moment of inertia as I1 and I2 respectively and mesh with a speed ratio ω2/ω1 = n then equivalent moment of inertia of both gears referred to first one is?a)n2I1 + I2b)I1 + nI2c)nI1 + I2d)I1 + n2I2Correct answer is option 'D'. Can you explain this answer?.
Solutions for If two gears have moment of inertia as I1 and I2 respectively and mesh with a speed ratio ω2/ω1 = n then equivalent moment of inertia of both gears referred to first one is?a)n2I1 + I2b)I1 + nI2c)nI1 + I2d)I1 + n2I2Correct answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for GATE.
Download more important topics, notes, lectures and mock test series for GATE Exam by signing up for free.
Here you can find the meaning of If two gears have moment of inertia as I1 and I2 respectively and mesh with a speed ratio ω2/ω1 = n then equivalent moment of inertia of both gears referred to first one is?a)n2I1 + I2b)I1 + nI2c)nI1 + I2d)I1 + n2I2Correct answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
If two gears have moment of inertia as I1 and I2 respectively and mesh with a speed ratio ω2/ω1 = n then equivalent moment of inertia of both gears referred to first one is?a)n2I1 + I2b)I1 + nI2c)nI1 + I2d)I1 + n2I2Correct answer is option 'D'. Can you explain this answer?, a detailed solution for If two gears have moment of inertia as I1 and I2 respectively and mesh with a speed ratio ω2/ω1 = n then equivalent moment of inertia of both gears referred to first one is?a)n2I1 + I2b)I1 + nI2c)nI1 + I2d)I1 + n2I2Correct answer is option 'D'. Can you explain this answer? has been provided alongside types of If two gears have moment of inertia as I1 and I2 respectively and mesh with a speed ratio ω2/ω1 = n then equivalent moment of inertia of both gears referred to first one is?a)n2I1 + I2b)I1 + nI2c)nI1 + I2d)I1 + n2I2Correct answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice If two gears have moment of inertia as I1 and I2 respectively and mesh with a speed ratio ω2/ω1 = n then equivalent moment of inertia of both gears referred to first one is?a)n2I1 + I2b)I1 + nI2c)nI1 + I2d)I1 + n2I2Correct answer is option 'D'. Can you explain this answer? tests, examples and also practice GATE tests.

|
Explore Courses for GATE exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















