GATE Exam > GATE Questions > A solid body formed by joining the base of a...
Start Learning for Free
A solid body formed by joining the base of a right circular cone of height equals to 150mm to the equal base of a right circular cylinder of height h = 45mm. Calculate the distance of the centre of mass of the solid from its plane face?
- a)70.65 mm
- b)54.08 mm
- c)80.65 mm
- d)75 mm
Correct answer is option 'B'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A solid body formed by joining the base of a right circular cone of h...
As the body is symmetrical about the vertical axis, therefore its centre of gravity will lie on this axis as shown in Fig. Let r be the radius of the cylinder base in cm. Now let base of the cylinder be the axis of reference.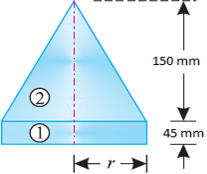
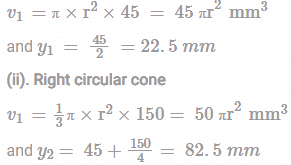
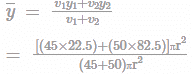
View all questions of this test

(i). Cylinder
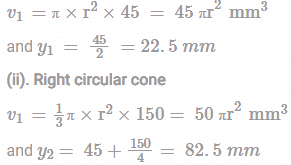
We know that distance between centre of gravity of the section and base of the cylinder
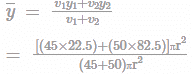
= 54.08 mm
Most Upvoted Answer
A solid body formed by joining the base of a right circular cone of h...
To find the distance of the centre of mass of the solid from its plane face, we need to find the centroid of the solid.
The solid is formed by joining the base of a right circular cone to the equal base of a right circular cylinder. Let's break down the problem into two parts - the cone and the cylinder.
1. Cone:
The cone has a height of 150 mm. The centroid of a cone lies at a distance of one-fourth of its height from the base. Therefore, the distance of the centroid of the cone from its base is (1/4) * 150 mm = 37.5 mm.
2. Cylinder:
The cylinder has a height of 45 mm. The centroid of a cylinder lies at the midpoint of its height. Therefore, the distance of the centroid of the cylinder from its base is (1/2) * 45 mm = 22.5 mm.
Now, since the base of the cone and the base of the cylinder are joined together, the centroid of the solid lies somewhere in between these distances.
To find the exact distance, we can use the principle of moments. The principle of moments states that the sum of the moments of all the forces acting on a body is zero. In this case, the forces are the weight of the cone and the weight of the cylinder.
Let's assume the distance of the centroid of the solid from the base of the cone is x mm. Therefore, the distance of the centroid from the base of the cylinder would be (150 - x) mm.
The moment of the weight of the cone about the base of the cylinder = weight of the cone * distance of the centroid of the cone from the base of the cylinder = (weight of the cone) * x mm
The moment of the weight of the cylinder about the base of the cone = weight of the cylinder * distance of the centroid of the cylinder from the base of the cone = (weight of the cylinder) * (150 - x) mm
Since the sum of the moments is zero, we can equate these two moments:
(weight of the cone) * x mm = (weight of the cylinder) * (150 - x) mm
Now, the weight of an object is given by the formula weight = mass * gravitational acceleration. Since the mass is proportional to the volume and the volume is proportional to the height, we can say that the weight of the cone is proportional to its height and the weight of the cylinder is proportional to its height.
Therefore, we can rewrite the equation as:
(height of the cone) * x mm = (height of the cylinder) * (150 - x) mm
Substituting the values, we get:
150 * x mm = 45 * (150 - x) mm
Simplifying the equation, we get:
150 * x = 45 * 150 - 45 * x
195 * x = 45 * 150
x = (45 * 150) / 195
x ≈ 34.62 mm
Therefore, the distance of the centroid of the solid from its plane face is approximately 34.62 mm.
The solid is formed by joining the base of a right circular cone to the equal base of a right circular cylinder. Let's break down the problem into two parts - the cone and the cylinder.
1. Cone:
The cone has a height of 150 mm. The centroid of a cone lies at a distance of one-fourth of its height from the base. Therefore, the distance of the centroid of the cone from its base is (1/4) * 150 mm = 37.5 mm.
2. Cylinder:
The cylinder has a height of 45 mm. The centroid of a cylinder lies at the midpoint of its height. Therefore, the distance of the centroid of the cylinder from its base is (1/2) * 45 mm = 22.5 mm.
Now, since the base of the cone and the base of the cylinder are joined together, the centroid of the solid lies somewhere in between these distances.
To find the exact distance, we can use the principle of moments. The principle of moments states that the sum of the moments of all the forces acting on a body is zero. In this case, the forces are the weight of the cone and the weight of the cylinder.
Let's assume the distance of the centroid of the solid from the base of the cone is x mm. Therefore, the distance of the centroid from the base of the cylinder would be (150 - x) mm.
The moment of the weight of the cone about the base of the cylinder = weight of the cone * distance of the centroid of the cone from the base of the cylinder = (weight of the cone) * x mm
The moment of the weight of the cylinder about the base of the cone = weight of the cylinder * distance of the centroid of the cylinder from the base of the cone = (weight of the cylinder) * (150 - x) mm
Since the sum of the moments is zero, we can equate these two moments:
(weight of the cone) * x mm = (weight of the cylinder) * (150 - x) mm
Now, the weight of an object is given by the formula weight = mass * gravitational acceleration. Since the mass is proportional to the volume and the volume is proportional to the height, we can say that the weight of the cone is proportional to its height and the weight of the cylinder is proportional to its height.
Therefore, we can rewrite the equation as:
(height of the cone) * x mm = (height of the cylinder) * (150 - x) mm
Substituting the values, we get:
150 * x mm = 45 * (150 - x) mm
Simplifying the equation, we get:
150 * x = 45 * 150 - 45 * x
195 * x = 45 * 150
x = (45 * 150) / 195
x ≈ 34.62 mm
Therefore, the distance of the centroid of the solid from its plane face is approximately 34.62 mm.

|
Explore Courses for GATE exam
|

|
A solid body formed by joining the base of a right circular cone of height equals to 150mm to the equal base of a right circular cylinder of height h = 45mm. Calculate the distance of the centre of mass of the solid from its plane face?a)70.65 mmb)54.08 mmc)80.65 mmd)75 mmCorrect answer is option 'B'. Can you explain this answer?
Question Description
A solid body formed by joining the base of a right circular cone of height equals to 150mm to the equal base of a right circular cylinder of height h = 45mm. Calculate the distance of the centre of mass of the solid from its plane face?a)70.65 mmb)54.08 mmc)80.65 mmd)75 mmCorrect answer is option 'B'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about A solid body formed by joining the base of a right circular cone of height equals to 150mm to the equal base of a right circular cylinder of height h = 45mm. Calculate the distance of the centre of mass of the solid from its plane face?a)70.65 mmb)54.08 mmc)80.65 mmd)75 mmCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A solid body formed by joining the base of a right circular cone of height equals to 150mm to the equal base of a right circular cylinder of height h = 45mm. Calculate the distance of the centre of mass of the solid from its plane face?a)70.65 mmb)54.08 mmc)80.65 mmd)75 mmCorrect answer is option 'B'. Can you explain this answer?.
A solid body formed by joining the base of a right circular cone of height equals to 150mm to the equal base of a right circular cylinder of height h = 45mm. Calculate the distance of the centre of mass of the solid from its plane face?a)70.65 mmb)54.08 mmc)80.65 mmd)75 mmCorrect answer is option 'B'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about A solid body formed by joining the base of a right circular cone of height equals to 150mm to the equal base of a right circular cylinder of height h = 45mm. Calculate the distance of the centre of mass of the solid from its plane face?a)70.65 mmb)54.08 mmc)80.65 mmd)75 mmCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A solid body formed by joining the base of a right circular cone of height equals to 150mm to the equal base of a right circular cylinder of height h = 45mm. Calculate the distance of the centre of mass of the solid from its plane face?a)70.65 mmb)54.08 mmc)80.65 mmd)75 mmCorrect answer is option 'B'. Can you explain this answer?.
Solutions for A solid body formed by joining the base of a right circular cone of height equals to 150mm to the equal base of a right circular cylinder of height h = 45mm. Calculate the distance of the centre of mass of the solid from its plane face?a)70.65 mmb)54.08 mmc)80.65 mmd)75 mmCorrect answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for GATE.
Download more important topics, notes, lectures and mock test series for GATE Exam by signing up for free.
Here you can find the meaning of A solid body formed by joining the base of a right circular cone of height equals to 150mm to the equal base of a right circular cylinder of height h = 45mm. Calculate the distance of the centre of mass of the solid from its plane face?a)70.65 mmb)54.08 mmc)80.65 mmd)75 mmCorrect answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A solid body formed by joining the base of a right circular cone of height equals to 150mm to the equal base of a right circular cylinder of height h = 45mm. Calculate the distance of the centre of mass of the solid from its plane face?a)70.65 mmb)54.08 mmc)80.65 mmd)75 mmCorrect answer is option 'B'. Can you explain this answer?, a detailed solution for A solid body formed by joining the base of a right circular cone of height equals to 150mm to the equal base of a right circular cylinder of height h = 45mm. Calculate the distance of the centre of mass of the solid from its plane face?a)70.65 mmb)54.08 mmc)80.65 mmd)75 mmCorrect answer is option 'B'. Can you explain this answer? has been provided alongside types of A solid body formed by joining the base of a right circular cone of height equals to 150mm to the equal base of a right circular cylinder of height h = 45mm. Calculate the distance of the centre of mass of the solid from its plane face?a)70.65 mmb)54.08 mmc)80.65 mmd)75 mmCorrect answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A solid body formed by joining the base of a right circular cone of height equals to 150mm to the equal base of a right circular cylinder of height h = 45mm. Calculate the distance of the centre of mass of the solid from its plane face?a)70.65 mmb)54.08 mmc)80.65 mmd)75 mmCorrect answer is option 'B'. Can you explain this answer? tests, examples and also practice GATE tests.

|
Explore Courses for GATE exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
















