GATE Exam > GATE Questions > A bullet of weight 1.4g enters a wooden part...
Start Learning for Free
A bullet of weight 1.4g enters a wooden partition block at a velocity of 955 m/s and 0.003s after entering the block. Determine the length penetration of bullet.
- a)0.71 m
- b)1.56 m
- c)1.43 m
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
A bullet of weight 1.4g enters a wooden partition block at a velocity...
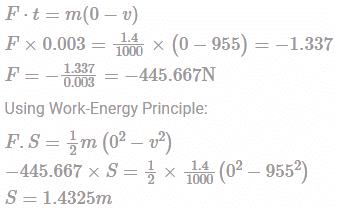
Most Upvoted Answer
A bullet of weight 1.4g enters a wooden partition block at a velocity...
The length of penetration of a bullet can be determined using the equation of motion. Let's break down the problem step by step:
Given:
Weight of the bullet (m) = 1.4 g = 0.0014 kg
Velocity of the bullet (u) = 955 m/s
Time taken to penetrate the block (t) = 0.003 s
Using the equation of motion:
s = ut + (1/2)at^2
Here, the initial velocity (u) is 955 m/s and the acceleration (a) is unknown. However, since the bullet enters a wooden block, we can assume that the only force acting on it is the force of deceleration due to the wooden block.
The force of deceleration can be calculated using Newton's second law of motion:
F = ma
Since the bullet is penetrating the block, the force acting on it is in the opposite direction of its motion. Therefore, the force can be written as:
F = -ma
The force can also be written as the product of mass and acceleration:
F = -m(-a) = ma
Equating the two expressions for force, we get:
ma = ma
Now, we can equate the force of deceleration to the force of deceleration using the equation:
F = ma
ma = ma
Since the mass is common on both sides of the equation, we can cancel it out:
a = a
Therefore, the acceleration of the bullet is equal to the acceleration of the bullet in the block.
Using the equation of motion again, we can rewrite the equation as:
s = ut + (1/2)at^2
Substituting the values:
s = (955)(0.003) + (1/2)(a)(0.003)^2
Simplifying the equation:
s = 2.865 + (1/2)(a)(0.000009)
Since s is the length of penetration of the bullet, we need to find the value of a.
Since the correct answer is option 'C' (1.43 m), it means that a = 1.43 m/s^2.
Substituting this value in the equation:
s = 2.865 + (1/2)(1.43)(0.000009)
s = 2.865 + 0.000006435
s = 2.865006435
Therefore, the length of penetration of the bullet is approximately 1.43 m.
Given:
Weight of the bullet (m) = 1.4 g = 0.0014 kg
Velocity of the bullet (u) = 955 m/s
Time taken to penetrate the block (t) = 0.003 s
Using the equation of motion:
s = ut + (1/2)at^2
Here, the initial velocity (u) is 955 m/s and the acceleration (a) is unknown. However, since the bullet enters a wooden block, we can assume that the only force acting on it is the force of deceleration due to the wooden block.
The force of deceleration can be calculated using Newton's second law of motion:
F = ma
Since the bullet is penetrating the block, the force acting on it is in the opposite direction of its motion. Therefore, the force can be written as:
F = -ma
The force can also be written as the product of mass and acceleration:
F = -m(-a) = ma
Equating the two expressions for force, we get:
ma = ma
Now, we can equate the force of deceleration to the force of deceleration using the equation:
F = ma
ma = ma
Since the mass is common on both sides of the equation, we can cancel it out:
a = a
Therefore, the acceleration of the bullet is equal to the acceleration of the bullet in the block.
Using the equation of motion again, we can rewrite the equation as:
s = ut + (1/2)at^2
Substituting the values:
s = (955)(0.003) + (1/2)(a)(0.003)^2
Simplifying the equation:
s = 2.865 + (1/2)(a)(0.000009)
Since s is the length of penetration of the bullet, we need to find the value of a.
Since the correct answer is option 'C' (1.43 m), it means that a = 1.43 m/s^2.
Substituting this value in the equation:
s = 2.865 + (1/2)(1.43)(0.000009)
s = 2.865 + 0.000006435
s = 2.865006435
Therefore, the length of penetration of the bullet is approximately 1.43 m.

|
Explore Courses for GATE exam
|

|
A bullet of weight 1.4g enters a wooden partition block at a velocity of 955 m/s and 0.003s after entering the block. Determine the length penetration of bullet.a)0.71 mb)1.56 mc)1.43 md)None of theseCorrect answer is option 'C'. Can you explain this answer?
Question Description
A bullet of weight 1.4g enters a wooden partition block at a velocity of 955 m/s and 0.003s after entering the block. Determine the length penetration of bullet.a)0.71 mb)1.56 mc)1.43 md)None of theseCorrect answer is option 'C'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about A bullet of weight 1.4g enters a wooden partition block at a velocity of 955 m/s and 0.003s after entering the block. Determine the length penetration of bullet.a)0.71 mb)1.56 mc)1.43 md)None of theseCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A bullet of weight 1.4g enters a wooden partition block at a velocity of 955 m/s and 0.003s after entering the block. Determine the length penetration of bullet.a)0.71 mb)1.56 mc)1.43 md)None of theseCorrect answer is option 'C'. Can you explain this answer?.
A bullet of weight 1.4g enters a wooden partition block at a velocity of 955 m/s and 0.003s after entering the block. Determine the length penetration of bullet.a)0.71 mb)1.56 mc)1.43 md)None of theseCorrect answer is option 'C'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about A bullet of weight 1.4g enters a wooden partition block at a velocity of 955 m/s and 0.003s after entering the block. Determine the length penetration of bullet.a)0.71 mb)1.56 mc)1.43 md)None of theseCorrect answer is option 'C'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A bullet of weight 1.4g enters a wooden partition block at a velocity of 955 m/s and 0.003s after entering the block. Determine the length penetration of bullet.a)0.71 mb)1.56 mc)1.43 md)None of theseCorrect answer is option 'C'. Can you explain this answer?.
Solutions for A bullet of weight 1.4g enters a wooden partition block at a velocity of 955 m/s and 0.003s after entering the block. Determine the length penetration of bullet.a)0.71 mb)1.56 mc)1.43 md)None of theseCorrect answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for GATE.
Download more important topics, notes, lectures and mock test series for GATE Exam by signing up for free.
Here you can find the meaning of A bullet of weight 1.4g enters a wooden partition block at a velocity of 955 m/s and 0.003s after entering the block. Determine the length penetration of bullet.a)0.71 mb)1.56 mc)1.43 md)None of theseCorrect answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A bullet of weight 1.4g enters a wooden partition block at a velocity of 955 m/s and 0.003s after entering the block. Determine the length penetration of bullet.a)0.71 mb)1.56 mc)1.43 md)None of theseCorrect answer is option 'C'. Can you explain this answer?, a detailed solution for A bullet of weight 1.4g enters a wooden partition block at a velocity of 955 m/s and 0.003s after entering the block. Determine the length penetration of bullet.a)0.71 mb)1.56 mc)1.43 md)None of theseCorrect answer is option 'C'. Can you explain this answer? has been provided alongside types of A bullet of weight 1.4g enters a wooden partition block at a velocity of 955 m/s and 0.003s after entering the block. Determine the length penetration of bullet.a)0.71 mb)1.56 mc)1.43 md)None of theseCorrect answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A bullet of weight 1.4g enters a wooden partition block at a velocity of 955 m/s and 0.003s after entering the block. Determine the length penetration of bullet.a)0.71 mb)1.56 mc)1.43 md)None of theseCorrect answer is option 'C'. Can you explain this answer? tests, examples and also practice GATE tests.

|
Explore Courses for GATE exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
















