NEET Exam > NEET Questions > A ray of light strikes a transparent rectangu...
Start Learning for Free
A ray of light strikes a transparent rectangular slab of refractive index √2 at an angle of incidence of 45°. The angle between the reflected and refracted rays is:
- a)75°
- b)90°
- c)105°
- d)120°
Correct answer is option 'C'. Can you explain this answer?
Verified Answer
A ray of light strikes a transparent rectangular slab of refractive in...
Applying Snell's law at air-glass surface, we get
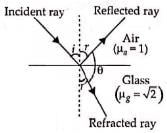
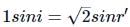
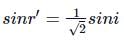
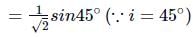
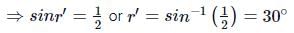

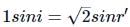
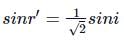
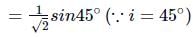
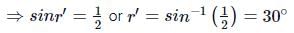
From figure,
i + θ + 30∘ = 180∘ (∵ i = r = 45∘)
45∘ + θ + 30∘ = 180∘ or
θ = 180∘ − 75∘ = 105∘
Hence, the angle between reflected and refracted rays is 105∘
i + θ + 30∘ = 180∘ (∵ i = r = 45∘)
45∘ + θ + 30∘ = 180∘ or
θ = 180∘ − 75∘ = 105∘
Hence, the angle between reflected and refracted rays is 105∘
Most Upvoted Answer
A ray of light strikes a transparent rectangular slab of refractive in...
Let's call the refractive index of the rectangular slab "n". When a ray of light strikes the slab, it will bend at the interface between the air and the slab due to the change in refractive index.
The angle of incidence (i) and the angle of refraction (r) can be related through Snell's law:
n1 * sin(i) = n2 * sin(r)
where n1 is the refractive index of the air (which is approximately 1) and n2 is the refractive index of the slab (which is given as "n" in the problem).
In this case, the ray of light is entering the slab from the air, so n1 = 1 and n2 = n. Let's assume that the incident ray is perpendicular to one of the faces of the rectangular slab (so i = 0). This means that the ray will not bend at the first interface.
However, when the ray reaches the second interface (between the slab and the air again), it will bend again due to the change in refractive index. The angle of refraction can be found using Snell's law again, this time with n1 = n and n2 = 1:
n * sin(r) = 1 * sin(theta)
where theta is the angle between the refracted ray and the normal to the surface.
Since the slab is rectangular, we can assume that the angle theta will be the same for both sides of the slab (i.e. the ray will be symmetric). Therefore, we can find theta by using the fact that the sum of the angles in a rectangle is 360 degrees:
theta + r + r + i = 360
Since i = 0, we can simplify this to:
theta + 2r = 360
Now we can solve for theta using the value we found for r from Snell's law:
n * sin(r) = sin(theta)
sin(theta) = n * sin(r) = n * sin(arcsin(1/n)) = sqrt(n^2 - 1)
(Note that we used the fact that sin(arcsin(x)) = x.)
Now we can use this value of theta to solve for the angle of refraction on the second interface:
theta + 2r = 360
r = (360 - theta)/2 = (360 - arcsin(sqrt(n^2 - 1)))/2
So we have found the angle of refraction on the second interface, and we can use this to determine the path of the refracted ray. We can also find the deviation angle of the ray by subtracting the incident angle from the final angle:
deviation angle = r - i = (360 - arcsin(sqrt(n^2 - 1)))/2
This expression gives us the amount that the ray is deflected as it passes through the rectangular slab.
The angle of incidence (i) and the angle of refraction (r) can be related through Snell's law:
n1 * sin(i) = n2 * sin(r)
where n1 is the refractive index of the air (which is approximately 1) and n2 is the refractive index of the slab (which is given as "n" in the problem).
In this case, the ray of light is entering the slab from the air, so n1 = 1 and n2 = n. Let's assume that the incident ray is perpendicular to one of the faces of the rectangular slab (so i = 0). This means that the ray will not bend at the first interface.
However, when the ray reaches the second interface (between the slab and the air again), it will bend again due to the change in refractive index. The angle of refraction can be found using Snell's law again, this time with n1 = n and n2 = 1:
n * sin(r) = 1 * sin(theta)
where theta is the angle between the refracted ray and the normal to the surface.
Since the slab is rectangular, we can assume that the angle theta will be the same for both sides of the slab (i.e. the ray will be symmetric). Therefore, we can find theta by using the fact that the sum of the angles in a rectangle is 360 degrees:
theta + r + r + i = 360
Since i = 0, we can simplify this to:
theta + 2r = 360
Now we can solve for theta using the value we found for r from Snell's law:
n * sin(r) = sin(theta)
sin(theta) = n * sin(r) = n * sin(arcsin(1/n)) = sqrt(n^2 - 1)
(Note that we used the fact that sin(arcsin(x)) = x.)
Now we can use this value of theta to solve for the angle of refraction on the second interface:
theta + 2r = 360
r = (360 - theta)/2 = (360 - arcsin(sqrt(n^2 - 1)))/2
So we have found the angle of refraction on the second interface, and we can use this to determine the path of the refracted ray. We can also find the deviation angle of the ray by subtracting the incident angle from the final angle:
deviation angle = r - i = (360 - arcsin(sqrt(n^2 - 1)))/2
This expression gives us the amount that the ray is deflected as it passes through the rectangular slab.

|
Explore Courses for NEET exam
|

|
Question Description
A ray of light strikes a transparent rectangular slab of refractive index √2 at an angle of incidence of 45°. The angle between the reflected and refracted rays is:a)75°b)90°c)105°d)120°Correct answer is option 'C'. Can you explain this answer? for NEET 2025 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about A ray of light strikes a transparent rectangular slab of refractive index √2 at an angle of incidence of 45°. The angle between the reflected and refracted rays is:a)75°b)90°c)105°d)120°Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for NEET 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A ray of light strikes a transparent rectangular slab of refractive index √2 at an angle of incidence of 45°. The angle between the reflected and refracted rays is:a)75°b)90°c)105°d)120°Correct answer is option 'C'. Can you explain this answer?.
A ray of light strikes a transparent rectangular slab of refractive index √2 at an angle of incidence of 45°. The angle between the reflected and refracted rays is:a)75°b)90°c)105°d)120°Correct answer is option 'C'. Can you explain this answer? for NEET 2025 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about A ray of light strikes a transparent rectangular slab of refractive index √2 at an angle of incidence of 45°. The angle between the reflected and refracted rays is:a)75°b)90°c)105°d)120°Correct answer is option 'C'. Can you explain this answer? covers all topics & solutions for NEET 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for A ray of light strikes a transparent rectangular slab of refractive index √2 at an angle of incidence of 45°. The angle between the reflected and refracted rays is:a)75°b)90°c)105°d)120°Correct answer is option 'C'. Can you explain this answer?.
Solutions for A ray of light strikes a transparent rectangular slab of refractive index √2 at an angle of incidence of 45°. The angle between the reflected and refracted rays is:a)75°b)90°c)105°d)120°Correct answer is option 'C'. Can you explain this answer? in English & in Hindi are available as part of our courses for NEET.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.
Here you can find the meaning of A ray of light strikes a transparent rectangular slab of refractive index √2 at an angle of incidence of 45°. The angle between the reflected and refracted rays is:a)75°b)90°c)105°d)120°Correct answer is option 'C'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
A ray of light strikes a transparent rectangular slab of refractive index √2 at an angle of incidence of 45°. The angle between the reflected and refracted rays is:a)75°b)90°c)105°d)120°Correct answer is option 'C'. Can you explain this answer?, a detailed solution for A ray of light strikes a transparent rectangular slab of refractive index √2 at an angle of incidence of 45°. The angle between the reflected and refracted rays is:a)75°b)90°c)105°d)120°Correct answer is option 'C'. Can you explain this answer? has been provided alongside types of A ray of light strikes a transparent rectangular slab of refractive index √2 at an angle of incidence of 45°. The angle between the reflected and refracted rays is:a)75°b)90°c)105°d)120°Correct answer is option 'C'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice A ray of light strikes a transparent rectangular slab of refractive index √2 at an angle of incidence of 45°. The angle between the reflected and refracted rays is:a)75°b)90°c)105°d)120°Correct answer is option 'C'. Can you explain this answer? tests, examples and also practice NEET tests.

|
Explore Courses for NEET exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















