GATE Exam > GATE Questions > Conversion of (98.75)10 into binary, octal an...
Start Learning for Free
Conversion of (98.75)10 into binary, octal and hexadecimal number system, respectively, is:
- a)(1100010.11)2 (246.6)8 and (62.C)16
- b)(0100011.11)2 (142.6)8 and (62.C)16
- c)(0100011.11)2 (242.6)8 and (62.12)16
- d)(1100010.11)2 (142.6)8 and (62.C)16
Correct answer is option 'D'. Can you explain this answer?
Most Upvoted Answer
Conversion of (98.75)10 into binary, octal and hexadecimal number syst...
Conversion of (98.75)10 into binary, octal and hexadecimal number system, respectively, is:
Step 1: Convert the integer part of the decimal number into the desired number system.
To convert the integer part of the decimal number into binary, octal and hexadecimal, we perform successive division by 2, 8 and 16 respectively until the quotient becomes zero. We write down the remainders in reverse order to get the binary, octal and hexadecimal equivalent of the integer part.
- Binary: 98 ÷ 2 = 49 remainder 0, 49 ÷ 2 = 24 remainder 1, 24 ÷ 2 = 12 remainder 0, 12 ÷ 2 = 6 remainder 0, 6 ÷ 2 = 3 remainder 0, 3 ÷ 2 = 1 remainder 1, 1 ÷ 2 = 0 remainder 1. Therefore, (98)10 = (1100010)2.
- Octal: 98 ÷ 8 = 12 remainder 2, 12 ÷ 8 = 1 remainder 4, 1 ÷ 8 = 0 remainder 1. Therefore, (98)10 = (142)8.
- Hexadecimal: 98 ÷ 16 = 6 remainder 2, 6 ÷ 16 = 0 remainder 6. Therefore, (98)10 = (62)16.
Step 2: Convert the fractional part of the decimal number into the desired number system.
To convert the fractional part of the decimal number into binary, octal and hexadecimal, we perform successive multiplication by 2, 8 and 16 respectively until the fractional part becomes zero or until we get the desired precision. We write down the integer part of each multiplication as the corresponding digit of the binary, octal or hexadecimal equivalent.
- Binary: 0.75 × 2 = 1.5 → 1, 0.5 × 2 = 1.0 → 1. Therefore, (0.75)10 = (0.11)2.
- Octal: 0.75 × 8 = 6.0 → 6. Therefore, (0.75)10 = (0.6)8.
- Hexadecimal: 0.75 × 16 = 12.0 → C. Therefore, (0.75)10 = (0.C)16.
Step 3: Combine the integer and fractional parts to get the final result.
- Binary: (98.75)10 = (1100010.11)2.
- Octal: (98.75)10 = (142.6)8.
- Hexadecimal: (98.75)10 = (62.C)16.
Therefore, the correct answer is option D.
Step 1: Convert the integer part of the decimal number into the desired number system.
To convert the integer part of the decimal number into binary, octal and hexadecimal, we perform successive division by 2, 8 and 16 respectively until the quotient becomes zero. We write down the remainders in reverse order to get the binary, octal and hexadecimal equivalent of the integer part.
- Binary: 98 ÷ 2 = 49 remainder 0, 49 ÷ 2 = 24 remainder 1, 24 ÷ 2 = 12 remainder 0, 12 ÷ 2 = 6 remainder 0, 6 ÷ 2 = 3 remainder 0, 3 ÷ 2 = 1 remainder 1, 1 ÷ 2 = 0 remainder 1. Therefore, (98)10 = (1100010)2.
- Octal: 98 ÷ 8 = 12 remainder 2, 12 ÷ 8 = 1 remainder 4, 1 ÷ 8 = 0 remainder 1. Therefore, (98)10 = (142)8.
- Hexadecimal: 98 ÷ 16 = 6 remainder 2, 6 ÷ 16 = 0 remainder 6. Therefore, (98)10 = (62)16.
Step 2: Convert the fractional part of the decimal number into the desired number system.
To convert the fractional part of the decimal number into binary, octal and hexadecimal, we perform successive multiplication by 2, 8 and 16 respectively until the fractional part becomes zero or until we get the desired precision. We write down the integer part of each multiplication as the corresponding digit of the binary, octal or hexadecimal equivalent.
- Binary: 0.75 × 2 = 1.5 → 1, 0.5 × 2 = 1.0 → 1. Therefore, (0.75)10 = (0.11)2.
- Octal: 0.75 × 8 = 6.0 → 6. Therefore, (0.75)10 = (0.6)8.
- Hexadecimal: 0.75 × 16 = 12.0 → C. Therefore, (0.75)10 = (0.C)16.
Step 3: Combine the integer and fractional parts to get the final result.
- Binary: (98.75)10 = (1100010.11)2.
- Octal: (98.75)10 = (142.6)8.
- Hexadecimal: (98.75)10 = (62.C)16.
Therefore, the correct answer is option D.
Free Test
FREE
| Start Free Test |
Community Answer
Conversion of (98.75)10 into binary, octal and hexadecimal number syst...
Concept:
Conversion of decimal to binary:
Step 1: Divide the number by 2 keeping notice of the quotient and the remainder. Continue dividing the quotient by 2 until you get a quotient of zero.
Step 2: Write out the remainders in the reverse order to get the equivalent binary number.
Conversion of decimal to binary:
Step 1: Divide the number by 2 keeping notice of the quotient and the remainder. Continue dividing the quotient by 2 until you get a quotient of zero.
Step 2: Write out the remainders in the reverse order to get the equivalent binary number.
For converting decimal fractions to binary numbers, follow these steps:
For converting decimal fractions to a binary numbers, follow these steps:
Then write out the integer parts from the results of each multiplication to get the equivalent binary number.
For converting decimal fractions to a binary numbers, follow these steps:
Then write out the integer parts from the results of each multiplication to get the equivalent binary number.
Conversion of binary to octal:
Make pair of three binary number which forms an octal number.
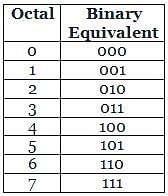
Make pair of three binary number which forms an octal number.

Conversion of binary to hexadecimal:
Make pair of four binary number which forms a hexadecimal number.
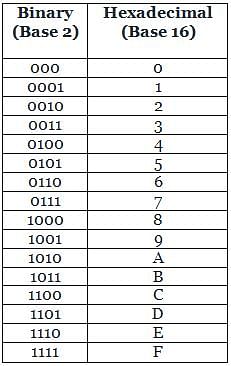
Make pair of four binary number which forms a hexadecimal number.

Calculation:
Given, that the decimal number = (98.75)10
98 / 2 = 49 with remainder 0
49 / 2 = 24 with remainder 1
24 / 2 = 12 with remainder 0
12 / 2 = 6 with remainder 0
6 / 2 = 3 with remainder 0
3 / 2 = 1 with remainder 1
1 / 2 = 0 with remainder 1
Given, that the decimal number = (98.75)10
98 / 2 = 49 with remainder 0
49 / 2 = 24 with remainder 1
24 / 2 = 12 with remainder 0
12 / 2 = 6 with remainder 0
6 / 2 = 3 with remainder 0
3 / 2 = 1 with remainder 1
1 / 2 = 0 with remainder 1
Write in reverse order:
98 = 1100010
0.75 × 2 = 1 + 0.5
0.5 × 2 = 1 + 0
.75 = .11
(98.75)10 = (1100010.11)2
(98.75)10 = (001 100 010. 110)2 = (142.6)8 ...........(from table 1)
(98.75)10 = (0110 0010. 1100)2 = (62.C)16...........(from table 2)
98 = 1100010
0.75 × 2 = 1 + 0.5
0.5 × 2 = 1 + 0
.75 = .11
(98.75)10 = (1100010.11)2
(98.75)10 = (001 100 010. 110)2 = (142.6)8 ...........(from table 1)
(98.75)10 = (0110 0010. 1100)2 = (62.C)16...........(from table 2)

|
Explore Courses for GATE exam
|

|
Similar GATE Doubts
Conversion of (98.75)10 into binary, octal and hexadecimal number system, respectively, is:a)(1100010.11)2 (246.6)8 and (62.C)16b)(0100011.11)2 (142.6)8 and (62.C)16c)(0100011.11)2 (242.6)8 and (62.12)16d)(1100010.11)2 (142.6)8 and (62.C)16Correct answer is option 'D'. Can you explain this answer?
Question Description
Conversion of (98.75)10 into binary, octal and hexadecimal number system, respectively, is:a)(1100010.11)2 (246.6)8 and (62.C)16b)(0100011.11)2 (142.6)8 and (62.C)16c)(0100011.11)2 (242.6)8 and (62.12)16d)(1100010.11)2 (142.6)8 and (62.C)16Correct answer is option 'D'. Can you explain this answer? for GATE 2025 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about Conversion of (98.75)10 into binary, octal and hexadecimal number system, respectively, is:a)(1100010.11)2 (246.6)8 and (62.C)16b)(0100011.11)2 (142.6)8 and (62.C)16c)(0100011.11)2 (242.6)8 and (62.12)16d)(1100010.11)2 (142.6)8 and (62.C)16Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for GATE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Conversion of (98.75)10 into binary, octal and hexadecimal number system, respectively, is:a)(1100010.11)2 (246.6)8 and (62.C)16b)(0100011.11)2 (142.6)8 and (62.C)16c)(0100011.11)2 (242.6)8 and (62.12)16d)(1100010.11)2 (142.6)8 and (62.C)16Correct answer is option 'D'. Can you explain this answer?.
Conversion of (98.75)10 into binary, octal and hexadecimal number system, respectively, is:a)(1100010.11)2 (246.6)8 and (62.C)16b)(0100011.11)2 (142.6)8 and (62.C)16c)(0100011.11)2 (242.6)8 and (62.12)16d)(1100010.11)2 (142.6)8 and (62.C)16Correct answer is option 'D'. Can you explain this answer? for GATE 2025 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about Conversion of (98.75)10 into binary, octal and hexadecimal number system, respectively, is:a)(1100010.11)2 (246.6)8 and (62.C)16b)(0100011.11)2 (142.6)8 and (62.C)16c)(0100011.11)2 (242.6)8 and (62.12)16d)(1100010.11)2 (142.6)8 and (62.C)16Correct answer is option 'D'. Can you explain this answer? covers all topics & solutions for GATE 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Conversion of (98.75)10 into binary, octal and hexadecimal number system, respectively, is:a)(1100010.11)2 (246.6)8 and (62.C)16b)(0100011.11)2 (142.6)8 and (62.C)16c)(0100011.11)2 (242.6)8 and (62.12)16d)(1100010.11)2 (142.6)8 and (62.C)16Correct answer is option 'D'. Can you explain this answer?.
Solutions for Conversion of (98.75)10 into binary, octal and hexadecimal number system, respectively, is:a)(1100010.11)2 (246.6)8 and (62.C)16b)(0100011.11)2 (142.6)8 and (62.C)16c)(0100011.11)2 (242.6)8 and (62.12)16d)(1100010.11)2 (142.6)8 and (62.C)16Correct answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for GATE.
Download more important topics, notes, lectures and mock test series for GATE Exam by signing up for free.
Here you can find the meaning of Conversion of (98.75)10 into binary, octal and hexadecimal number system, respectively, is:a)(1100010.11)2 (246.6)8 and (62.C)16b)(0100011.11)2 (142.6)8 and (62.C)16c)(0100011.11)2 (242.6)8 and (62.12)16d)(1100010.11)2 (142.6)8 and (62.C)16Correct answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Conversion of (98.75)10 into binary, octal and hexadecimal number system, respectively, is:a)(1100010.11)2 (246.6)8 and (62.C)16b)(0100011.11)2 (142.6)8 and (62.C)16c)(0100011.11)2 (242.6)8 and (62.12)16d)(1100010.11)2 (142.6)8 and (62.C)16Correct answer is option 'D'. Can you explain this answer?, a detailed solution for Conversion of (98.75)10 into binary, octal and hexadecimal number system, respectively, is:a)(1100010.11)2 (246.6)8 and (62.C)16b)(0100011.11)2 (142.6)8 and (62.C)16c)(0100011.11)2 (242.6)8 and (62.12)16d)(1100010.11)2 (142.6)8 and (62.C)16Correct answer is option 'D'. Can you explain this answer? has been provided alongside types of Conversion of (98.75)10 into binary, octal and hexadecimal number system, respectively, is:a)(1100010.11)2 (246.6)8 and (62.C)16b)(0100011.11)2 (142.6)8 and (62.C)16c)(0100011.11)2 (242.6)8 and (62.12)16d)(1100010.11)2 (142.6)8 and (62.C)16Correct answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Conversion of (98.75)10 into binary, octal and hexadecimal number system, respectively, is:a)(1100010.11)2 (246.6)8 and (62.C)16b)(0100011.11)2 (142.6)8 and (62.C)16c)(0100011.11)2 (242.6)8 and (62.12)16d)(1100010.11)2 (142.6)8 and (62.C)16Correct answer is option 'D'. Can you explain this answer? tests, examples and also practice GATE tests.

|
Explore Courses for GATE exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.



















