A pulse train with a frequency of 1 MHz is counted using a mod-1024 ripple counter built with J-K flip-flops. For proper operation of the counter the maximum permissible propagation delay per flip-flop stage isa)100 nsb)50 nsc)20 nsd)10 nsCorrect answer is option 'A'. Can you explain this answer?

Question

Answer

Concept:

If we pass the input signal to a single T-flip flop, we will get half of the frequency at the output.

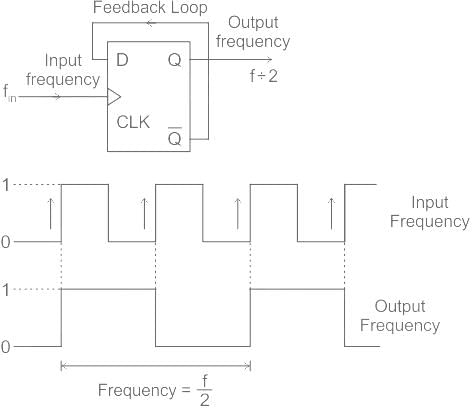
Similarly, when we pass the input signal into a divide by M bit counter, the output frequency (f_out) will be:

Calculation:

Given is a mod-1024 ripple counter which means that it can count 1024 states.

To count 1024 number of flipflop required is:

1024 = 2ⁿ

n = 10 flip-flops

t_pdff = Propagation delay of flip flops

tpdff = 10^-6 sec.

Propagation delay per flipflop =

= 10⁻⁶/10

= 100 nsec

Answer

Understanding the Problem
To determine the maximum permissible propagation delay for each flip-flop in a mod-1024 ripple counter, we must first understand the requirements of counting pulses.
Ripple Counter Basics
- A ripple counter consists of several flip-flops where the output of one flip-flop serves as the clock input for the next.
- For a mod-1024 counter, 10 flip-flops are needed since $2^{10} = 1024$.
Frequency of the Input Signal
- The input pulse train has a frequency of 1 MHz, which translates to a period ($T$) of:
$$
T = \frac{1}{f} = \frac{1}{1 \text{ MHz}} = 1 \mu s = 1000 ns
$$
Propagation Delay Considerations
- The total propagation delay ($t_{pd}$) for the ripple counter is the time taken for the output of the first flip-flop to propagate through all 10 flip-flops.
- Each flip-flop contributes a propagation delay, so for 10 flip-flops, we have:
$$
t_{pd(total)} = 10 \times t_{pd(flip-flop)}
$$
Timing Constraints
- For the ripple counter to function correctly, the total propagation delay must be less than or equal to the clock period (1000 ns):
$$
10 \times t_{pd(flip-flop)} \leq 1000 ns
$$
- Rearranging gives:
$$
t_{pd(flip-flop)} \leq \frac{1000 ns}{10} = 100 ns
$$
Conclusion
- The maximum permissible propagation delay per flip-flop stage is therefore 100 ns, making option (a) the correct answer.
- This ensures that each flip-flop can reliably toggle before the next clock pulse arrives, maintaining proper counting operation.

Similar Electrical Engineering (EE) Doubts

A pulse train with a frequency of 1 MHz is counted using a mod-1024 ripple counter built with J-K flip-flops. For proper operation of the counter the maximum permissible propagation delay per flip-flop stage is

A pulse train with a frequency of 1MHz is counted using a mod-1024 ripple counter built with J–K flip-flops. For proper operation of the counter the maximum permissible propagation delay per flip-flop stage is

An eight stage ripple counter uses a flip-flop with propagation delay of 75 nano-seconds. The pulse width of the strobe is 50 nano-seconds. The frequency of the input signal which can be used for proper operation of the counter is approximately equal to

The maximum clock frequency in MHz of a 4-stage ripple counter, utilizing flip-flops, with each flip-flop having a propagation delay of 20 ns, is ___________. (round off to one decimal plac e) Correct answer is between '12.3,12.7'. Can you explain this answer?

The maximum clock frequency in MHz of a 4-stage ripple counter, utilizing flip-flops, with each flip-flop having a propagation delay of 20 ns, is ____ . (round off to one decimal plac e). Correct answer is '12.5'. Can you explain this answer?

Top Courses for Electrical Engineering (EE)View all

Network Theory (Electric Circuits)

GATE Electrical Engineering (EE) Mock Test Series 2026

General Aptitude for GATE

GATE Notes & Videos for Electrical Engineering

Engineering Mathematics

Top Courses for Electrical Engineering (EE)

Top Courses for Electrical Engineering (EE)

Related Content

Mock Test Series

Subject-wise Courses

Subject-wise Courses

Other Engg Branches

Company