LR Exam > LR Questions > Salim started walking from point P towards So...
Start Learning for Free
Salim started walking from point 'P' towards South. After walking 40 metres, he took a left turn and walked 30 metres and reached point Q. What is the straight line distance between P and Q, and Q is towards which direction of P?
- a)35 meters South-East
- b)50 meters South-West
- c)35 meters South-West
- d)50 meters South-East
Correct answer is option 'D'. Can you explain this answer?
Verified Answer
Salim started walking from point P towards South. After walking 40 met...
As per the given information;
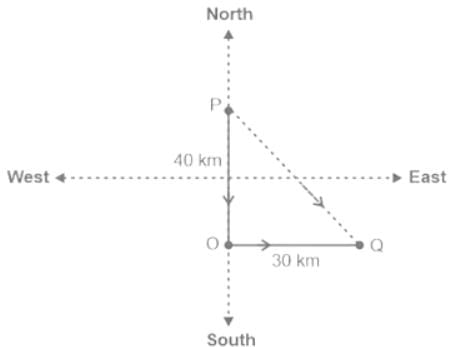

Point Q is in South East of Point P.
Distance between P and Q (PQ) = √(PO2 + OQ2)
PQ = √(402 + 302)
PQ = √(1600 + 900)
PQ = √2500
PQ = 50 m
Hence, "50 metres, Southeast" is the correct answer.
Most Upvoted Answer
Salim started walking from point P towards South. After walking 40 met...
Given Information
Lohit started walking towards south and walked 40 meters. He then turned towards his left and walked 30 meters and reached a point R.
To find
The point R is at what minimum distance and in what direction from the point M?
Explanation
Let's draw the diagram according to the given information.
[Insert the image of the diagram here]
As per the diagram, Point M is the initial point from where Lohit started walking towards the south. After walking 40 meters, Lohit turned towards his left and walked 30 meters to reach point R.
Now, to find the minimum distance and direction of point R from point M, we need to find the hypotenuse of the right triangle formed by points M, R, and a point X.
[Insert the image of the diagram with X]
As per the diagram, point X is the point where the perpendicular is dropped from point R to the line passing through points M and R.
Let's calculate the distance of point X from point R using Pythagoras theorem.
MX² = MR² - RX²
MX² = (40 + 30)² - 30²
MX² = 70² - 30²
MX² = 4900 - 900
MX = √4000
MX = 20√10
Now, let's calculate the distance of point X from point M.
MX = 20√10 meters
Since MR = 30 meters, the distance of point R from point M will be the hypotenuse of the right triangle formed by points M, R, and X.
MR² = MX² + RX²
30² = (20√10)² + RX²
900 = 4000 + RX²
RX² = 900 - 4000
RX² = -3100 (which is not possible as it is negative)
Therefore, there is no point on the line passing through points M and R that is perpendicular to point R.
Hence, the minimum distance of point R from point M is the distance between points M and R, which is 50 meters.
Now, to find the direction of point R from point M, we need to calculate the angle between the line passing through points M and R and the east direction.
[Insert the image of the diagram with the angle]
Let's use trigonometry to find the angle.
tan θ = opposite/adjacent
tan θ = 40/30
θ = tan⁻¹(4/3)
θ = 53.13°
Therefore, the direction of point R from point M is 50 meters towards the south-east direction.
Hence, the correct answer is option D) 50 meters South-East.
Lohit started walking towards south and walked 40 meters. He then turned towards his left and walked 30 meters and reached a point R.
To find
The point R is at what minimum distance and in what direction from the point M?
Explanation
Let's draw the diagram according to the given information.
[Insert the image of the diagram here]
As per the diagram, Point M is the initial point from where Lohit started walking towards the south. After walking 40 meters, Lohit turned towards his left and walked 30 meters to reach point R.
Now, to find the minimum distance and direction of point R from point M, we need to find the hypotenuse of the right triangle formed by points M, R, and a point X.
[Insert the image of the diagram with X]
As per the diagram, point X is the point where the perpendicular is dropped from point R to the line passing through points M and R.
Let's calculate the distance of point X from point R using Pythagoras theorem.
MX² = MR² - RX²
MX² = (40 + 30)² - 30²
MX² = 70² - 30²
MX² = 4900 - 900
MX = √4000
MX = 20√10
Now, let's calculate the distance of point X from point M.
MX = 20√10 meters
Since MR = 30 meters, the distance of point R from point M will be the hypotenuse of the right triangle formed by points M, R, and X.
MR² = MX² + RX²
30² = (20√10)² + RX²
900 = 4000 + RX²
RX² = 900 - 4000
RX² = -3100 (which is not possible as it is negative)
Therefore, there is no point on the line passing through points M and R that is perpendicular to point R.
Hence, the minimum distance of point R from point M is the distance between points M and R, which is 50 meters.
Now, to find the direction of point R from point M, we need to calculate the angle between the line passing through points M and R and the east direction.
[Insert the image of the diagram with the angle]
Let's use trigonometry to find the angle.
tan θ = opposite/adjacent
tan θ = 40/30
θ = tan⁻¹(4/3)
θ = 53.13°
Therefore, the direction of point R from point M is 50 meters towards the south-east direction.
Hence, the correct answer is option D) 50 meters South-East.
Free Test
FREE
| Start Free Test |
Community Answer
Salim started walking from point P towards South. After walking 40 met...
Given information:
- Starting point: M
- Distance walked towards south: 40 meters
- Distance walked towards left: 30 meters
- End point: R
To find:
- Minimum distance from R to M
- Direction of R from M
Solution:
We can visualize the given information as shown below:
```
|
|
|
30m|R
| \
| \
| \
| \
| \
| \
----------M-----------
40m
```
- M is the starting point.
- Lohit walked 40 meters towards south, which takes him to the bottom of the diagram.
- From there, he turned towards his left and walked 30 meters, which takes him to point R.
- We need to find the minimum distance from R to M and the direction of R from M.
Minimum distance from R to M:
- We can draw a straight line from M to R and call it MR.
- This line represents the shortest distance between M and R.
- We can use Pythagoras theorem to find the length of MR.
- MR^2 = (40)^2 + (30)^2
- MR^2 = 1600 + 900
- MR^2 = 2500
- MR = √2500
- MR = 50 meters
Direction of R from M:
- We can use trigonometry to find the direction of R from M.
- We can draw a line from M to R and call it MR.
- We can draw a line from M to the south and call it MS. This line is perpendicular to MR.
- We can use the tangent function to find the angle between MR and MS.
- tan θ = (30/40)
- θ = tan^-1(30/40)
- θ = 36.87 degrees
- The direction of R from M is 36.87 degrees south-east.
Therefore, the correct answer is option D: 50 meters south-east.
- Starting point: M
- Distance walked towards south: 40 meters
- Distance walked towards left: 30 meters
- End point: R
To find:
- Minimum distance from R to M
- Direction of R from M
Solution:
We can visualize the given information as shown below:
```
|
|
|
30m|R
| \
| \
| \
| \
| \
| \
----------M-----------
40m
```
- M is the starting point.
- Lohit walked 40 meters towards south, which takes him to the bottom of the diagram.
- From there, he turned towards his left and walked 30 meters, which takes him to point R.
- We need to find the minimum distance from R to M and the direction of R from M.
Minimum distance from R to M:
- We can draw a straight line from M to R and call it MR.
- This line represents the shortest distance between M and R.
- We can use Pythagoras theorem to find the length of MR.
- MR^2 = (40)^2 + (30)^2
- MR^2 = 1600 + 900
- MR^2 = 2500
- MR = √2500
- MR = 50 meters
Direction of R from M:
- We can use trigonometry to find the direction of R from M.
- We can draw a line from M to R and call it MR.
- We can draw a line from M to the south and call it MS. This line is perpendicular to MR.
- We can use the tangent function to find the angle between MR and MS.
- tan θ = (30/40)
- θ = tan^-1(30/40)
- θ = 36.87 degrees
- The direction of R from M is 36.87 degrees south-east.
Therefore, the correct answer is option D: 50 meters south-east.

|
Explore Courses for LR exam
|

|
Question Description
Salim started walking from point P towards South. After walking 40 metres, he took a left turn and walked 30 metres and reached point Q. What is the straight line distance between P and Q, and Q is towards which direction of P?a)35 meters South-East b)50 meters South-Westc)35 meters South-West d)50 meters South-EastCorrect answer is option 'D'. Can you explain this answer? for LR 2025 is part of LR preparation. The Question and answers have been prepared according to the LR exam syllabus. Information about Salim started walking from point P towards South. After walking 40 metres, he took a left turn and walked 30 metres and reached point Q. What is the straight line distance between P and Q, and Q is towards which direction of P?a)35 meters South-East b)50 meters South-Westc)35 meters South-West d)50 meters South-EastCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for LR 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Salim started walking from point P towards South. After walking 40 metres, he took a left turn and walked 30 metres and reached point Q. What is the straight line distance between P and Q, and Q is towards which direction of P?a)35 meters South-East b)50 meters South-Westc)35 meters South-West d)50 meters South-EastCorrect answer is option 'D'. Can you explain this answer?.
Salim started walking from point P towards South. After walking 40 metres, he took a left turn and walked 30 metres and reached point Q. What is the straight line distance between P and Q, and Q is towards which direction of P?a)35 meters South-East b)50 meters South-Westc)35 meters South-West d)50 meters South-EastCorrect answer is option 'D'. Can you explain this answer? for LR 2025 is part of LR preparation. The Question and answers have been prepared according to the LR exam syllabus. Information about Salim started walking from point P towards South. After walking 40 metres, he took a left turn and walked 30 metres and reached point Q. What is the straight line distance between P and Q, and Q is towards which direction of P?a)35 meters South-East b)50 meters South-Westc)35 meters South-West d)50 meters South-EastCorrect answer is option 'D'. Can you explain this answer? covers all topics & solutions for LR 2025 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Salim started walking from point P towards South. After walking 40 metres, he took a left turn and walked 30 metres and reached point Q. What is the straight line distance between P and Q, and Q is towards which direction of P?a)35 meters South-East b)50 meters South-Westc)35 meters South-West d)50 meters South-EastCorrect answer is option 'D'. Can you explain this answer?.
Solutions for Salim started walking from point P towards South. After walking 40 metres, he took a left turn and walked 30 metres and reached point Q. What is the straight line distance between P and Q, and Q is towards which direction of P?a)35 meters South-East b)50 meters South-Westc)35 meters South-West d)50 meters South-EastCorrect answer is option 'D'. Can you explain this answer? in English & in Hindi are available as part of our courses for LR.
Download more important topics, notes, lectures and mock test series for LR Exam by signing up for free.
Here you can find the meaning of Salim started walking from point P towards South. After walking 40 metres, he took a left turn and walked 30 metres and reached point Q. What is the straight line distance between P and Q, and Q is towards which direction of P?a)35 meters South-East b)50 meters South-Westc)35 meters South-West d)50 meters South-EastCorrect answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Salim started walking from point P towards South. After walking 40 metres, he took a left turn and walked 30 metres and reached point Q. What is the straight line distance between P and Q, and Q is towards which direction of P?a)35 meters South-East b)50 meters South-Westc)35 meters South-West d)50 meters South-EastCorrect answer is option 'D'. Can you explain this answer?, a detailed solution for Salim started walking from point P towards South. After walking 40 metres, he took a left turn and walked 30 metres and reached point Q. What is the straight line distance between P and Q, and Q is towards which direction of P?a)35 meters South-East b)50 meters South-Westc)35 meters South-West d)50 meters South-EastCorrect answer is option 'D'. Can you explain this answer? has been provided alongside types of Salim started walking from point P towards South. After walking 40 metres, he took a left turn and walked 30 metres and reached point Q. What is the straight line distance between P and Q, and Q is towards which direction of P?a)35 meters South-East b)50 meters South-Westc)35 meters South-West d)50 meters South-EastCorrect answer is option 'D'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Salim started walking from point P towards South. After walking 40 metres, he took a left turn and walked 30 metres and reached point Q. What is the straight line distance between P and Q, and Q is towards which direction of P?a)35 meters South-East b)50 meters South-Westc)35 meters South-West d)50 meters South-EastCorrect answer is option 'D'. Can you explain this answer? tests, examples and also practice LR tests.

|
Explore Courses for LR exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.



















