LR Exam > LR Questions > Speed of a boat in standing water is 14 kmph ...
Start Learning for Free
Speed of a boat in standing water is 14 kmph and the speed of the stream is 1.2 kmph. A man rows to a place at a distance of 4864 km and comes back to the starting point. The total time taken by him is:
- a)700 hours
- b)350 hours
- c)1400 hours
- d)1010 hours
Correct answer is option 'A'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
Speed of a boat in standing water is 14 kmph and the speed of the stre...
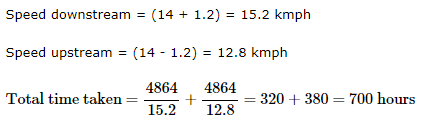
Most Upvoted Answer
Speed of a boat in standing water is 14 kmph and the speed of the stre...
Speed downstream = (14 + 1.2)
= 15.2kmph
Speed upstream = (14-1.2)
= 12.8kmph
Total time taken = 4864/15.2 + 4864/12.8
= 320 + 380
= 700hrs
= 15.2kmph
Speed upstream = (14-1.2)
= 12.8kmph
Total time taken = 4864/15.2 + 4864/12.8
= 320 + 380
= 700hrs
Free Test
FREE
| Start Free Test |
Community Answer
Speed of a boat in standing water is 14 kmph and the speed of the stre...
Given:
Speed of the boat in standing water = 14 kmph
Speed of the stream = 1.2 kmph
Distance to be covered = 4864 km
To Find:
Total time taken by the man to row to the place and come back to the starting point.
The speed of the boat in standing water is the actual speed at which the boat can travel.
The speed of the stream affects the overall speed of the boat when rowing against or along the stream.
The speed of the boat in still water is 14 kmph.
The speed of the stream is 1.2 kmph.
When the boat is rowing against the stream, the effective speed of the boat is reduced by the speed of the stream.
So the speed of the boat while rowing against the stream will be 14 - 1.2 = 12.8 kmph.
When the boat is rowing along the stream, the effective speed of the boat is increased by the speed of the stream.
So the speed of the boat while rowing along the stream will be 14 + 1.2 = 15.2 kmph.
The total distance to be covered is 4864 km.
The total time taken to row to the place and come back can be calculated as follows:
Time taken to row to the place = Distance / Speed = 4864 / 12.8 = 380 hours (approx.)
Time taken to row back to the starting point = Distance / Speed = 4864 / 15.2 = 320 hours (approx.)
Total time taken = Time taken to row to the place + Time taken to row back = 380 + 320 = 700 hours (approx.)
Therefore, the total time taken by the man to row to the place and come back to the starting point is approximately 700 hours.
Answer:
The correct answer is option A) 700 hours.
Speed of the boat in standing water = 14 kmph
Speed of the stream = 1.2 kmph
Distance to be covered = 4864 km
To Find:
Total time taken by the man to row to the place and come back to the starting point.
Concept:
The speed of the boat in standing water is the actual speed at which the boat can travel.
The speed of the stream affects the overall speed of the boat when rowing against or along the stream.
Calculation:
The speed of the boat in still water is 14 kmph.
The speed of the stream is 1.2 kmph.
When the boat is rowing against the stream, the effective speed of the boat is reduced by the speed of the stream.
So the speed of the boat while rowing against the stream will be 14 - 1.2 = 12.8 kmph.
When the boat is rowing along the stream, the effective speed of the boat is increased by the speed of the stream.
So the speed of the boat while rowing along the stream will be 14 + 1.2 = 15.2 kmph.
The total distance to be covered is 4864 km.
The total time taken to row to the place and come back can be calculated as follows:
Time taken to row to the place = Distance / Speed = 4864 / 12.8 = 380 hours (approx.)
Time taken to row back to the starting point = Distance / Speed = 4864 / 15.2 = 320 hours (approx.)
Total time taken = Time taken to row to the place + Time taken to row back = 380 + 320 = 700 hours (approx.)
Therefore, the total time taken by the man to row to the place and come back to the starting point is approximately 700 hours.
Answer:
The correct answer is option A) 700 hours.
|
Explore Courses for LR exam
|
|
Similar LR Doubts
Speed of a boat in standing water is 14 kmph and the speed of the stream is 1.2 kmph. A man rows to a place at a distance of 4864 km and comes back to the starting point. The total time taken by him is:
a)700 hoursb)350 hoursc)1400 hoursd)1010 hoursCorrect answer is option 'A'. Can you explain this answer?
Question Description
Speed of a boat in standing water is 14 kmph and the speed of the stream is 1.2 kmph. A man rows to a place at a distance of 4864 km and comes back to the starting point. The total time taken by him is: a)700 hoursb)350 hoursc)1400 hoursd)1010 hoursCorrect answer is option 'A'. Can you explain this answer? for LR 2024 is part of LR preparation. The Question and answers have been prepared according to the LR exam syllabus. Information about Speed of a boat in standing water is 14 kmph and the speed of the stream is 1.2 kmph. A man rows to a place at a distance of 4864 km and comes back to the starting point. The total time taken by him is: a)700 hoursb)350 hoursc)1400 hoursd)1010 hoursCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for LR 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Speed of a boat in standing water is 14 kmph and the speed of the stream is 1.2 kmph. A man rows to a place at a distance of 4864 km and comes back to the starting point. The total time taken by him is: a)700 hoursb)350 hoursc)1400 hoursd)1010 hoursCorrect answer is option 'A'. Can you explain this answer?.
Speed of a boat in standing water is 14 kmph and the speed of the stream is 1.2 kmph. A man rows to a place at a distance of 4864 km and comes back to the starting point. The total time taken by him is: a)700 hoursb)350 hoursc)1400 hoursd)1010 hoursCorrect answer is option 'A'. Can you explain this answer? for LR 2024 is part of LR preparation. The Question and answers have been prepared according to the LR exam syllabus. Information about Speed of a boat in standing water is 14 kmph and the speed of the stream is 1.2 kmph. A man rows to a place at a distance of 4864 km and comes back to the starting point. The total time taken by him is: a)700 hoursb)350 hoursc)1400 hoursd)1010 hoursCorrect answer is option 'A'. Can you explain this answer? covers all topics & solutions for LR 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Speed of a boat in standing water is 14 kmph and the speed of the stream is 1.2 kmph. A man rows to a place at a distance of 4864 km and comes back to the starting point. The total time taken by him is: a)700 hoursb)350 hoursc)1400 hoursd)1010 hoursCorrect answer is option 'A'. Can you explain this answer?.
Solutions for Speed of a boat in standing water is 14 kmph and the speed of the stream is 1.2 kmph. A man rows to a place at a distance of 4864 km and comes back to the starting point. The total time taken by him is:
a)700 hoursb)350 hoursc)1400 hoursd)1010 hoursCorrect answer is option 'A'. Can you explain this answer? in English & in Hindi are available as part of our courses for LR.
Download more important topics, notes, lectures and mock test series for LR Exam by signing up for free.
Here you can find the meaning of Speed of a boat in standing water is 14 kmph and the speed of the stream is 1.2 kmph. A man rows to a place at a distance of 4864 km and comes back to the starting point. The total time taken by him is:
a)700 hoursb)350 hoursc)1400 hoursd)1010 hoursCorrect answer is option 'A'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
Speed of a boat in standing water is 14 kmph and the speed of the stream is 1.2 kmph. A man rows to a place at a distance of 4864 km and comes back to the starting point. The total time taken by him is:
a)700 hoursb)350 hoursc)1400 hoursd)1010 hoursCorrect answer is option 'A'. Can you explain this answer?, a detailed solution for Speed of a boat in standing water is 14 kmph and the speed of the stream is 1.2 kmph. A man rows to a place at a distance of 4864 km and comes back to the starting point. The total time taken by him is:
a)700 hoursb)350 hoursc)1400 hoursd)1010 hoursCorrect answer is option 'A'. Can you explain this answer? has been provided alongside types of Speed of a boat in standing water is 14 kmph and the speed of the stream is 1.2 kmph. A man rows to a place at a distance of 4864 km and comes back to the starting point. The total time taken by him is:
a)700 hoursb)350 hoursc)1400 hoursd)1010 hoursCorrect answer is option 'A'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice Speed of a boat in standing water is 14 kmph and the speed of the stream is 1.2 kmph. A man rows to a place at a distance of 4864 km and comes back to the starting point. The total time taken by him is:
a)700 hoursb)350 hoursc)1400 hoursd)1010 hoursCorrect answer is option 'A'. Can you explain this answer? tests, examples and also practice LR tests.
|
|
Explore Courses for LR exam
|
|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup