GATE Exam > GATE Questions > For a steady incompressible laminar flow betw...
Start Learning for Free
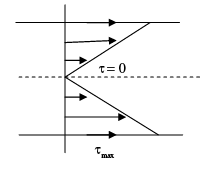
For a steady incompressible laminar flow between two infinite parallel stationary plates, the shear stress variation is
- a)linear with zero value at the plates
- b)linear with zero value at the center
- c)quadratic with zero value at the Plates
- d)quadratic with zero value at the centre
Correct answer is option 'B'. Can you explain this answer?
| FREE This question is part of | Download PDF Attempt this Test |
Verified Answer
For a steady incompressible laminar flow between two infinite parallel...
We know that velocity variation,
Most Upvoted Answer
For a steady incompressible laminar flow between two infinite parallel...
Steady Incompressible Laminar Flow between Two Infinite Parallel Stationary Plates
In a steady incompressible laminar flow between two infinite parallel stationary plates, the flow is characterized by the absence of turbulence and a constant velocity profile across the cross-section of the flow. This type of flow is commonly encountered in various engineering applications such as lubrication, flow in pipes, and boundary layer flows.
Shear Stress Variation
The shear stress is the force per unit area acting tangentially to the flow direction. In this flow configuration, the velocity of the fluid varies across the channel, resulting in a velocity gradient. This velocity gradient gives rise to a shear stress distribution within the fluid.
Linear Variation of Shear Stress
The correct answer to the given question is option 'B': linear with zero value at the center. This means that the shear stress variation across the channel is linear, and the maximum shear stress occurs at the walls of the channel, while the shear stress is zero at the center.
Explanations
1. Boundary Conditions: At the walls of the channel (i.e., at the plates), the fluid velocity is zero due to the no-slip condition. This implies that the fluid particles at the walls are stationary, and therefore there is no relative motion between the fluid and the walls. As a result, the shear stress is zero at the walls.
2. Velocity Profile: Due to the no-slip condition, the fluid velocity is maximum at the center of the channel and decreases linearly towards the walls. This velocity profile leads to a linear velocity gradient across the channel.
3. Shear Stress Calculation: The shear stress can be calculated using the equation: shear stress = dynamic viscosity × velocity gradient. In this flow configuration, the velocity gradient is linear, and therefore the shear stress variation is also linear.
4. Zero Shear Stress at the Center: At the center of the channel, the velocity gradient is zero, as the velocity is constant. Consequently, the shear stress is also zero at the center.
Conclusion
In a steady incompressible laminar flow between two infinite parallel stationary plates, the shear stress variation is linear with zero value at the center. This is due to the no-slip condition at the walls, which results in a linear velocity gradient across the channel. Understanding the shear stress variation is essential for analyzing fluid flow and designing various engineering systems.
In a steady incompressible laminar flow between two infinite parallel stationary plates, the flow is characterized by the absence of turbulence and a constant velocity profile across the cross-section of the flow. This type of flow is commonly encountered in various engineering applications such as lubrication, flow in pipes, and boundary layer flows.
Shear Stress Variation
The shear stress is the force per unit area acting tangentially to the flow direction. In this flow configuration, the velocity of the fluid varies across the channel, resulting in a velocity gradient. This velocity gradient gives rise to a shear stress distribution within the fluid.
Linear Variation of Shear Stress
The correct answer to the given question is option 'B': linear with zero value at the center. This means that the shear stress variation across the channel is linear, and the maximum shear stress occurs at the walls of the channel, while the shear stress is zero at the center.
Explanations
1. Boundary Conditions: At the walls of the channel (i.e., at the plates), the fluid velocity is zero due to the no-slip condition. This implies that the fluid particles at the walls are stationary, and therefore there is no relative motion between the fluid and the walls. As a result, the shear stress is zero at the walls.
2. Velocity Profile: Due to the no-slip condition, the fluid velocity is maximum at the center of the channel and decreases linearly towards the walls. This velocity profile leads to a linear velocity gradient across the channel.
3. Shear Stress Calculation: The shear stress can be calculated using the equation: shear stress = dynamic viscosity × velocity gradient. In this flow configuration, the velocity gradient is linear, and therefore the shear stress variation is also linear.
4. Zero Shear Stress at the Center: At the center of the channel, the velocity gradient is zero, as the velocity is constant. Consequently, the shear stress is also zero at the center.
Conclusion
In a steady incompressible laminar flow between two infinite parallel stationary plates, the shear stress variation is linear with zero value at the center. This is due to the no-slip condition at the walls, which results in a linear velocity gradient across the channel. Understanding the shear stress variation is essential for analyzing fluid flow and designing various engineering systems.
Free Test
FREE
| Start Free Test |
Community Answer
For a steady incompressible laminar flow between two infinite parallel...
X-2y=0

|
Explore Courses for GATE exam
|

|
Similar GATE Doubts
For a steady incompressible laminar flow between two infinite parallel stationary plates, the shear stress variation is a)linear with zero value at the platesb)linear with zero value at the centerc)quadratic with zero value at the Platesd)quadratic with zero value at the centreCorrect answer is option 'B'. Can you explain this answer?
Question Description
For a steady incompressible laminar flow between two infinite parallel stationary plates, the shear stress variation is a)linear with zero value at the platesb)linear with zero value at the centerc)quadratic with zero value at the Platesd)quadratic with zero value at the centreCorrect answer is option 'B'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about For a steady incompressible laminar flow between two infinite parallel stationary plates, the shear stress variation is a)linear with zero value at the platesb)linear with zero value at the centerc)quadratic with zero value at the Platesd)quadratic with zero value at the centreCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for For a steady incompressible laminar flow between two infinite parallel stationary plates, the shear stress variation is a)linear with zero value at the platesb)linear with zero value at the centerc)quadratic with zero value at the Platesd)quadratic with zero value at the centreCorrect answer is option 'B'. Can you explain this answer?.
For a steady incompressible laminar flow between two infinite parallel stationary plates, the shear stress variation is a)linear with zero value at the platesb)linear with zero value at the centerc)quadratic with zero value at the Platesd)quadratic with zero value at the centreCorrect answer is option 'B'. Can you explain this answer? for GATE 2024 is part of GATE preparation. The Question and answers have been prepared according to the GATE exam syllabus. Information about For a steady incompressible laminar flow between two infinite parallel stationary plates, the shear stress variation is a)linear with zero value at the platesb)linear with zero value at the centerc)quadratic with zero value at the Platesd)quadratic with zero value at the centreCorrect answer is option 'B'. Can you explain this answer? covers all topics & solutions for GATE 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for For a steady incompressible laminar flow between two infinite parallel stationary plates, the shear stress variation is a)linear with zero value at the platesb)linear with zero value at the centerc)quadratic with zero value at the Platesd)quadratic with zero value at the centreCorrect answer is option 'B'. Can you explain this answer?.
Solutions for For a steady incompressible laminar flow between two infinite parallel stationary plates, the shear stress variation is a)linear with zero value at the platesb)linear with zero value at the centerc)quadratic with zero value at the Platesd)quadratic with zero value at the centreCorrect answer is option 'B'. Can you explain this answer? in English & in Hindi are available as part of our courses for GATE.
Download more important topics, notes, lectures and mock test series for GATE Exam by signing up for free.
Here you can find the meaning of For a steady incompressible laminar flow between two infinite parallel stationary plates, the shear stress variation is a)linear with zero value at the platesb)linear with zero value at the centerc)quadratic with zero value at the Platesd)quadratic with zero value at the centreCorrect answer is option 'B'. Can you explain this answer? defined & explained in the simplest way possible. Besides giving the explanation of
For a steady incompressible laminar flow between two infinite parallel stationary plates, the shear stress variation is a)linear with zero value at the platesb)linear with zero value at the centerc)quadratic with zero value at the Platesd)quadratic with zero value at the centreCorrect answer is option 'B'. Can you explain this answer?, a detailed solution for For a steady incompressible laminar flow between two infinite parallel stationary plates, the shear stress variation is a)linear with zero value at the platesb)linear with zero value at the centerc)quadratic with zero value at the Platesd)quadratic with zero value at the centreCorrect answer is option 'B'. Can you explain this answer? has been provided alongside types of For a steady incompressible laminar flow between two infinite parallel stationary plates, the shear stress variation is a)linear with zero value at the platesb)linear with zero value at the centerc)quadratic with zero value at the Platesd)quadratic with zero value at the centreCorrect answer is option 'B'. Can you explain this answer? theory, EduRev gives you an
ample number of questions to practice For a steady incompressible laminar flow between two infinite parallel stationary plates, the shear stress variation is a)linear with zero value at the platesb)linear with zero value at the centerc)quadratic with zero value at the Platesd)quadratic with zero value at the centreCorrect answer is option 'B'. Can you explain this answer? tests, examples and also practice GATE tests.

|
Explore Courses for GATE exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.


















