NEET Exam > NEET Questions > The vector sum of two forces is perpendrcular...
Start Learning for Free
The vector sum of two forces is perpendrcular to their vector differences. In that case, the forces (a) are not equal to each other in magnitude (b) cannot be predicted (c) are equal to each other (d) are equal to each other in magnitude?
Verified Answer
The vector sum of two forces is perpendrcular to their vector differen...
The two diagonals of a parallelogram formed by two vectors represent the vector sum and vector difference of two vectors.
When the parallelogram is a square, the diagonals are perpendicular. Then, the two force vectors are represented by the adjacent sides of the square. Hence, the two force vectors which are equal in magnitude and perpendicular to each other have their vector sum perpendicular to their vector difference.
 This question is part of UPSC exam. View all NEET courses
This question is part of UPSC exam. View all NEET courses
Most Upvoted Answer
The vector sum of two forces is perpendrcular to their vector differen...
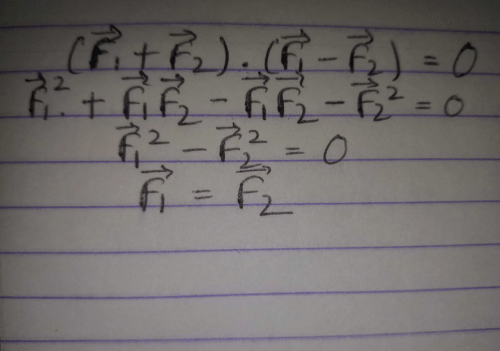
Community Answer
The vector sum of two forces is perpendrcular to their vector differen...
The Vector Sum and Difference of Forces
The problem states that the vector sum of two forces is perpendicular to their vector difference. Let's analyze this situation and determine the relationship between the magnitudes of the forces.
Understanding Vector Addition and Subtraction
In physics, forces are represented by vectors, which have both magnitude and direction. When two forces act on an object, their effects combine through vector addition or subtraction.
- Vector Addition: When forces act in the same direction, their magnitudes are added together to find the resultant force. The resultant force has the same direction as the individual forces.
- Vector Subtraction: When forces act in opposite directions, their magnitudes are subtracted to find the resultant force. The resultant force points in the direction of the larger force.
Vector Sum and Difference Relationship
According to the problem statement, the vector sum of the two forces is perpendicular to their vector difference. This means that the resultant force, obtained by adding or subtracting the forces, is orthogonal to the force that is not used in the calculation.
Analysis of Possible Scenarios
Based on the given information, we can consider the following scenarios:
(a) The forces are not equal to each other in magnitude:
If the forces have different magnitudes, their vector sum will not be equal to their vector difference. Therefore, this scenario does not satisfy the condition stated in the problem.
(b) The forces cannot be predicted:
Since the problem provides a specific relationship between the vector sum and difference, the forces can be predicted based on this relationship. Therefore, this scenario is not applicable.
(c) The forces are equal to each other:
If the forces are equal in magnitude, their vector sum will be equal to their vector difference. This scenario fulfills the condition mentioned in the problem.
(d) The forces are equal to each other in magnitude:
This scenario is the same as option (c) and satisfies the condition stated in the problem.
Conclusion
Based on the given information, the forces must be equal to each other in magnitude for their vector sum to be perpendicular to their vector difference. Options (c) and (d) both indicate that the forces are equal, but option (d) emphasizes that they are equal in magnitude.
Note: It is important to note that the given problem does not provide enough information to determine the exact magnitudes or directions of the forces. The analysis is solely based on the relationship between the vector sum and difference.
The problem states that the vector sum of two forces is perpendicular to their vector difference. Let's analyze this situation and determine the relationship between the magnitudes of the forces.
Understanding Vector Addition and Subtraction
In physics, forces are represented by vectors, which have both magnitude and direction. When two forces act on an object, their effects combine through vector addition or subtraction.
- Vector Addition: When forces act in the same direction, their magnitudes are added together to find the resultant force. The resultant force has the same direction as the individual forces.
- Vector Subtraction: When forces act in opposite directions, their magnitudes are subtracted to find the resultant force. The resultant force points in the direction of the larger force.
Vector Sum and Difference Relationship
According to the problem statement, the vector sum of the two forces is perpendicular to their vector difference. This means that the resultant force, obtained by adding or subtracting the forces, is orthogonal to the force that is not used in the calculation.
Analysis of Possible Scenarios
Based on the given information, we can consider the following scenarios:
(a) The forces are not equal to each other in magnitude:
If the forces have different magnitudes, their vector sum will not be equal to their vector difference. Therefore, this scenario does not satisfy the condition stated in the problem.
(b) The forces cannot be predicted:
Since the problem provides a specific relationship between the vector sum and difference, the forces can be predicted based on this relationship. Therefore, this scenario is not applicable.
(c) The forces are equal to each other:
If the forces are equal in magnitude, their vector sum will be equal to their vector difference. This scenario fulfills the condition mentioned in the problem.
(d) The forces are equal to each other in magnitude:
This scenario is the same as option (c) and satisfies the condition stated in the problem.
Conclusion
Based on the given information, the forces must be equal to each other in magnitude for their vector sum to be perpendicular to their vector difference. Options (c) and (d) both indicate that the forces are equal, but option (d) emphasizes that they are equal in magnitude.
Note: It is important to note that the given problem does not provide enough information to determine the exact magnitudes or directions of the forces. The analysis is solely based on the relationship between the vector sum and difference.
Attention NEET Students!
To make sure you are not studying endlessly, EduRev has designed NEET study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in NEET.

|
Explore Courses for NEET exam
|

|
Similar NEET Doubts
The vector sum of two forces is perpendrcular to their vector differences. In that case, the forces (a) are not equal to each other in magnitude (b) cannot be predicted (c) are equal to each other (d) are equal to each other in magnitude?
Question Description
The vector sum of two forces is perpendrcular to their vector differences. In that case, the forces (a) are not equal to each other in magnitude (b) cannot be predicted (c) are equal to each other (d) are equal to each other in magnitude? for NEET 2024 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about The vector sum of two forces is perpendrcular to their vector differences. In that case, the forces (a) are not equal to each other in magnitude (b) cannot be predicted (c) are equal to each other (d) are equal to each other in magnitude? covers all topics & solutions for NEET 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The vector sum of two forces is perpendrcular to their vector differences. In that case, the forces (a) are not equal to each other in magnitude (b) cannot be predicted (c) are equal to each other (d) are equal to each other in magnitude?.
The vector sum of two forces is perpendrcular to their vector differences. In that case, the forces (a) are not equal to each other in magnitude (b) cannot be predicted (c) are equal to each other (d) are equal to each other in magnitude? for NEET 2024 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about The vector sum of two forces is perpendrcular to their vector differences. In that case, the forces (a) are not equal to each other in magnitude (b) cannot be predicted (c) are equal to each other (d) are equal to each other in magnitude? covers all topics & solutions for NEET 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for The vector sum of two forces is perpendrcular to their vector differences. In that case, the forces (a) are not equal to each other in magnitude (b) cannot be predicted (c) are equal to each other (d) are equal to each other in magnitude?.
Solutions for The vector sum of two forces is perpendrcular to their vector differences. In that case, the forces (a) are not equal to each other in magnitude (b) cannot be predicted (c) are equal to each other (d) are equal to each other in magnitude? in English & in Hindi are available as part of our courses for NEET.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.
Here you can find the meaning of The vector sum of two forces is perpendrcular to their vector differences. In that case, the forces (a) are not equal to each other in magnitude (b) cannot be predicted (c) are equal to each other (d) are equal to each other in magnitude? defined & explained in the simplest way possible. Besides giving the explanation of
The vector sum of two forces is perpendrcular to their vector differences. In that case, the forces (a) are not equal to each other in magnitude (b) cannot be predicted (c) are equal to each other (d) are equal to each other in magnitude?, a detailed solution for The vector sum of two forces is perpendrcular to their vector differences. In that case, the forces (a) are not equal to each other in magnitude (b) cannot be predicted (c) are equal to each other (d) are equal to each other in magnitude? has been provided alongside types of The vector sum of two forces is perpendrcular to their vector differences. In that case, the forces (a) are not equal to each other in magnitude (b) cannot be predicted (c) are equal to each other (d) are equal to each other in magnitude? theory, EduRev gives you an
ample number of questions to practice The vector sum of two forces is perpendrcular to their vector differences. In that case, the forces (a) are not equal to each other in magnitude (b) cannot be predicted (c) are equal to each other (d) are equal to each other in magnitude? tests, examples and also practice NEET tests.

|
Explore Courses for NEET exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.

























