NEET Exam > NEET Questions > Keeping the mass of the earth constant if it'...
Start Learning for Free
Keeping the mass of the earth constant if it's radius is reduced to 1/4of it's initial value ,then the period of revolution of earth on its own axis and passing through the center is a)12 b)3?
Verified Answer
Keeping the mass of the earth constant if it's radius is reduced to 1/...
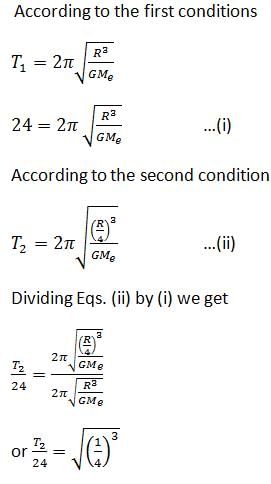
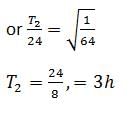
 This question is part of UPSC exam. View all NEET courses
This question is part of UPSC exam. View all NEET courses
Most Upvoted Answer
Keeping the mass of the earth constant if it's radius is reduced to 1/...
Reduction in Earth's Radius and Conservation of Mass
When the radius of the Earth is reduced to 1/4 of its initial value, it means that the new radius becomes one-fourth of the original radius. Let's denote the initial radius as R and the new radius as R/4.
According to the conservation of mass, the mass of an object remains constant regardless of changes in its size or shape. Therefore, even though the radius of the Earth is reduced, its mass will remain the same.
Period of Revolution of Earth on its Own Axis and Passing Through the Center
The period of revolution of the Earth on its own axis refers to the time it takes for the Earth to complete one full rotation. This period is commonly known as a day.
The period of revolution of the Earth passing through the center refers to the time it takes for the Earth to complete one orbit around the Sun. This period is commonly known as a year.
Effect of Radius Reduction on the Periods
The period of revolution of the Earth on its own axis:
The period of revolution of the Earth on its own axis is determined by the rotational speed of the Earth. The rotational speed is influenced by the distribution of mass and the radius of the Earth.
When the radius of the Earth is reduced to 1/4 of its initial value, the distribution of mass remains the same, but the radius decreases. This reduction in radius results in a decrease in the rotational speed of the Earth.
The formula for the period of revolution of an object on its own axis is given by:
T = 2π√(I/mr)
where T is the period of revolution, I is the moment of inertia, m is the mass, and r is the radius.
Since the mass of the Earth remains constant, the moment of inertia (I) will also remain constant. However, the reduction in radius (r) will cause a decrease in the period of revolution (T) of the Earth on its own axis.
The period of revolution of the Earth passing through the center:
The period of revolution of the Earth passing through the center is determined by the gravitational force between the Earth and the Sun. This force depends on the masses of the Earth and the Sun, as well as the distance between them.
When the radius of the Earth is reduced to 1/4 of its initial value, the distance between the Earth and the Sun will also decrease. This reduction in distance will result in an increase in the gravitational force between the Earth and the Sun.
The formula for the period of revolution of an object in circular orbit is given by:
T = 2π√(r^3/GM)
where T is the period of revolution, r is the radius, G is the gravitational constant, and M is the mass of the central object (in this case, the Sun).
Since the mass of the Earth remains constant, the period of revolution (T) of the Earth passing through the center will depend on the radius (r) and the mass of the Sun (M). The decrease in radius will result in a decrease in the period of revolution (T) of the Earth passing through the center.
Conclusion
In conclusion, when the radius of the Earth is reduced to 1/4 of its initial value while keeping the mass constant, the period of revolution of the Earth on its
When the radius of the Earth is reduced to 1/4 of its initial value, it means that the new radius becomes one-fourth of the original radius. Let's denote the initial radius as R and the new radius as R/4.
According to the conservation of mass, the mass of an object remains constant regardless of changes in its size or shape. Therefore, even though the radius of the Earth is reduced, its mass will remain the same.
Period of Revolution of Earth on its Own Axis and Passing Through the Center
The period of revolution of the Earth on its own axis refers to the time it takes for the Earth to complete one full rotation. This period is commonly known as a day.
The period of revolution of the Earth passing through the center refers to the time it takes for the Earth to complete one orbit around the Sun. This period is commonly known as a year.
Effect of Radius Reduction on the Periods
The period of revolution of the Earth on its own axis:
The period of revolution of the Earth on its own axis is determined by the rotational speed of the Earth. The rotational speed is influenced by the distribution of mass and the radius of the Earth.
When the radius of the Earth is reduced to 1/4 of its initial value, the distribution of mass remains the same, but the radius decreases. This reduction in radius results in a decrease in the rotational speed of the Earth.
The formula for the period of revolution of an object on its own axis is given by:
T = 2π√(I/mr)
where T is the period of revolution, I is the moment of inertia, m is the mass, and r is the radius.
Since the mass of the Earth remains constant, the moment of inertia (I) will also remain constant. However, the reduction in radius (r) will cause a decrease in the period of revolution (T) of the Earth on its own axis.
The period of revolution of the Earth passing through the center:
The period of revolution of the Earth passing through the center is determined by the gravitational force between the Earth and the Sun. This force depends on the masses of the Earth and the Sun, as well as the distance between them.
When the radius of the Earth is reduced to 1/4 of its initial value, the distance between the Earth and the Sun will also decrease. This reduction in distance will result in an increase in the gravitational force between the Earth and the Sun.
The formula for the period of revolution of an object in circular orbit is given by:
T = 2π√(r^3/GM)
where T is the period of revolution, r is the radius, G is the gravitational constant, and M is the mass of the central object (in this case, the Sun).
Since the mass of the Earth remains constant, the period of revolution (T) of the Earth passing through the center will depend on the radius (r) and the mass of the Sun (M). The decrease in radius will result in a decrease in the period of revolution (T) of the Earth passing through the center.
Conclusion
In conclusion, when the radius of the Earth is reduced to 1/4 of its initial value while keeping the mass constant, the period of revolution of the Earth on its
Attention NEET Students!
To make sure you are not studying endlessly, EduRev has designed NEET study material, with Structured Courses, Videos, & Test Series. Plus get personalized analysis, doubt solving and improvement plans to achieve a great score in NEET.

|
Explore Courses for NEET exam
|

|
Similar NEET Doubts
Keeping the mass of the earth constant if it's radius is reduced to 1/4of it's initial value ,then the period of revolution of earth on its own axis and passing through the center is a)12 b)3?
Question Description
Keeping the mass of the earth constant if it's radius is reduced to 1/4of it's initial value ,then the period of revolution of earth on its own axis and passing through the center is a)12 b)3? for NEET 2024 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about Keeping the mass of the earth constant if it's radius is reduced to 1/4of it's initial value ,then the period of revolution of earth on its own axis and passing through the center is a)12 b)3? covers all topics & solutions for NEET 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Keeping the mass of the earth constant if it's radius is reduced to 1/4of it's initial value ,then the period of revolution of earth on its own axis and passing through the center is a)12 b)3?.
Keeping the mass of the earth constant if it's radius is reduced to 1/4of it's initial value ,then the period of revolution of earth on its own axis and passing through the center is a)12 b)3? for NEET 2024 is part of NEET preparation. The Question and answers have been prepared according to the NEET exam syllabus. Information about Keeping the mass of the earth constant if it's radius is reduced to 1/4of it's initial value ,then the period of revolution of earth on its own axis and passing through the center is a)12 b)3? covers all topics & solutions for NEET 2024 Exam. Find important definitions, questions, meanings, examples, exercises and tests below for Keeping the mass of the earth constant if it's radius is reduced to 1/4of it's initial value ,then the period of revolution of earth on its own axis and passing through the center is a)12 b)3?.
Solutions for Keeping the mass of the earth constant if it's radius is reduced to 1/4of it's initial value ,then the period of revolution of earth on its own axis and passing through the center is a)12 b)3? in English & in Hindi are available as part of our courses for NEET.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.
Here you can find the meaning of Keeping the mass of the earth constant if it's radius is reduced to 1/4of it's initial value ,then the period of revolution of earth on its own axis and passing through the center is a)12 b)3? defined & explained in the simplest way possible. Besides giving the explanation of
Keeping the mass of the earth constant if it's radius is reduced to 1/4of it's initial value ,then the period of revolution of earth on its own axis and passing through the center is a)12 b)3?, a detailed solution for Keeping the mass of the earth constant if it's radius is reduced to 1/4of it's initial value ,then the period of revolution of earth on its own axis and passing through the center is a)12 b)3? has been provided alongside types of Keeping the mass of the earth constant if it's radius is reduced to 1/4of it's initial value ,then the period of revolution of earth on its own axis and passing through the center is a)12 b)3? theory, EduRev gives you an
ample number of questions to practice Keeping the mass of the earth constant if it's radius is reduced to 1/4of it's initial value ,then the period of revolution of earth on its own axis and passing through the center is a)12 b)3? tests, examples and also practice NEET tests.

|
Explore Courses for NEET exam
|

|
Suggested Free Tests
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.




















