Introduction to Units & Measurements | Physics Class 11 - NEET PDF Download
Introduction
- When thinking about building a house, it's important for architects and builders to measure things like walls and beams.
- They need to use the same units of measurement, such as meters or feet, to ensure everything fits together properly.
- If one team uses meters and another team uses feet, it could lead to serious issues. For example,
Suppose two teams are working together to build a bridge:
Team A uses meters and designs a beam that is 6 meters long.
Team B uses feet and makes a supporting pillar 15 feet tall.
When it's time to assemble, the team must ensure that the beam fits exactly on the pillar. But the units are different!
1 meter = 3.281 feet.
If Team A's 6-meter-long beam is converted to feet:
6 meters × 3.281 feet meter = 19.686 feet
The beam is actually 19.686 feet, while the pillar is only 15 feet tall, so they won’t fit properly.
This mismatch could lead to structural problems in the bridge.

- This mismatch could make the house unsafe, and it would require repairs, which would take extra time and cost more money.
- Using the correct units and taking accurate measurements is crucial, just like following a recipe to ensure successful outcomes.
- These practices help ensure that everything comes together correctly and safely.
Let's study measurements and their units in detail, in this document.
What are Physical Quantities?
The quantities that can be measured by an instrument and by which laws of physics can be described are called physical quantities.
A physical quantity has two main characteristics: the numerical magnitude and the unit of measurement.
For Example, mass can be quantified as n kg, where n is the numerical value and kg is the unit.
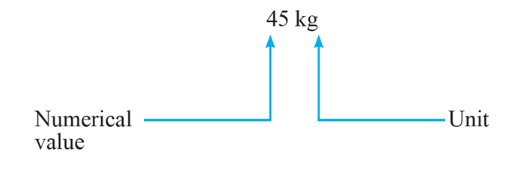
Physical quantity = numerical value and unit (n x u)
While expressing a definite amount of physical quantity, it is clear that as the unit (u) changes, the magnitude (n) will also change but product ‘nu’ will remain same.

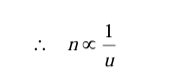 i.e. magnitude of a physical quantity and units are inversely proportional to each other.
i.e. magnitude of a physical quantity and units are inversely proportional to each other.
Larger the unit, smaller will be the magnitude.
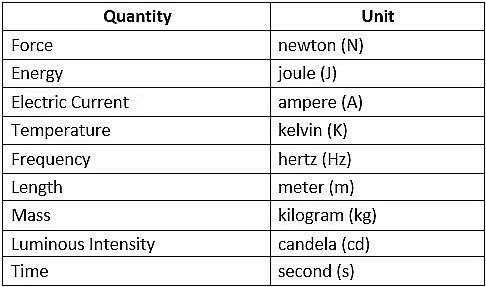
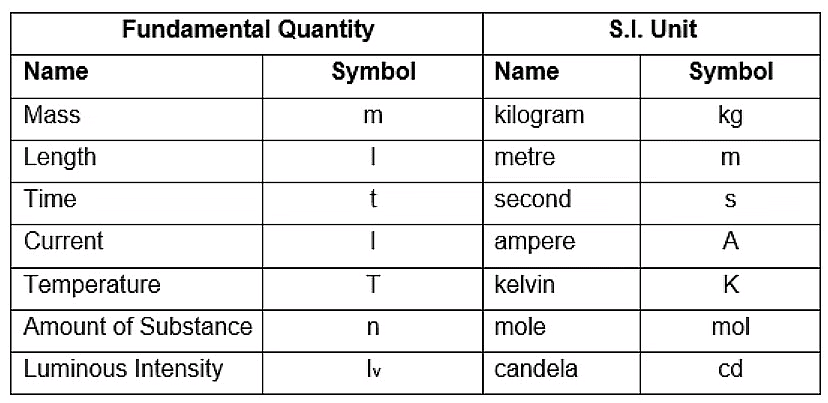
In physics, there are seven fundamental physical quantities that are measured in base or physical fundamental units:
1. Length
2. Mass
3. Time
4. Electric Current
5. Temperature
6. Amount of Substance
7. Luminous Intensity
 Basic Physical Quantities with symbols and definitions
Basic Physical Quantities with symbols and definitions
Fundamental and Derived Quantities
1. Fundamental Quantities
- There are only a few physical quantities in nature that are independent of others and don't need any additional quantities to be defined.
- These are called absolute quantities, or fundamental/base quantities.
- In short, all other physical quantities are built upon and expressed using these fundamental quantities.
2. Derived Quantities
- Any other physical quantities can be calculated by multiplying or dividing the powers of fundamental quantities.
- In short, derived quantities are generated from fundamental quantities through mathematical operations.
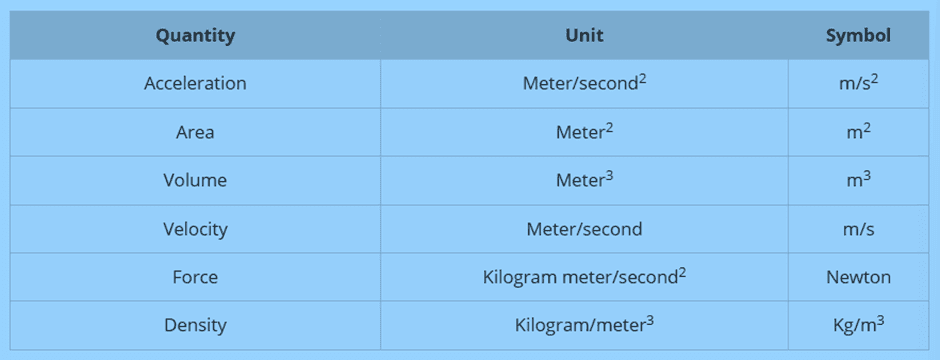
Example: Length is a fundamental quantity, while area and volume are derived from it.
Area = Length², and Volume = Length³.
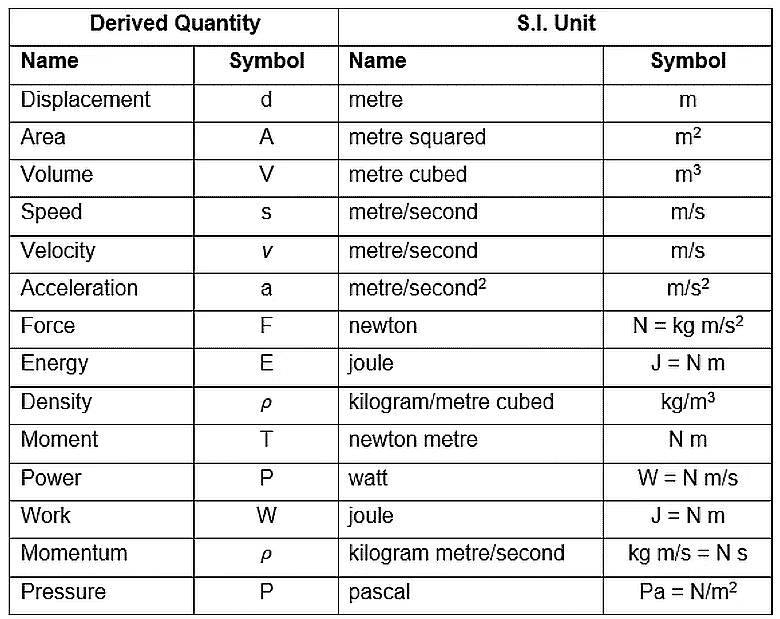
The table below shows some of the derived units:
System of Units
A complete set of units, both fundamental and derived, for all kinds of physical quantities, is called the system of units.
- To measure a physical quantity we require a standard of measurement. This standard is called the unit of that physical quantity.
- The system of units was introduced by the General Conference on Weight and Measures in 1971 and was accepted internationally.
- It has 7 basic units with 2 complementary units.
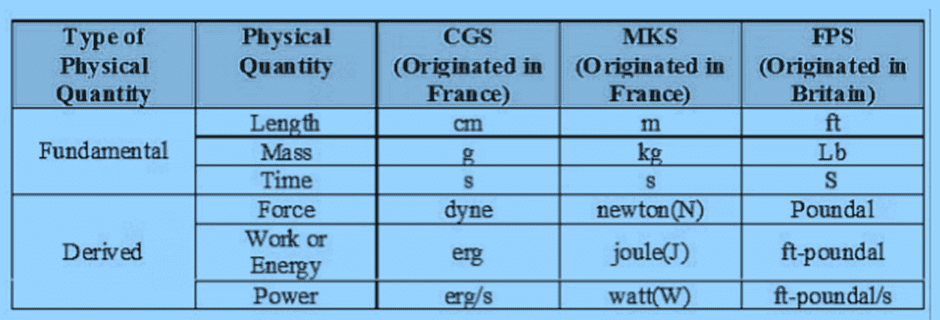
Some commonly used systems include:
- CGS System (Gaussian System): Fundamental quantities are length, mass, and time.
Corresponding units: centimetre (cm), gram (g), and second (s). - MKS System (Giorgi System): Uses length, mass, and time as fundamental quantities.
Corresponding units: metre (m), kilogram (kg), and second (s). - FPS System: Measures length, mass, and time using different units.
Units: foot (ft), pound (lb), and second (s). - S.I. System (International System): It is the global standard for units in physics.
Consists of seven fundamental quantities with corresponding units, covering all aspects of physics.
Here is the summarised table:
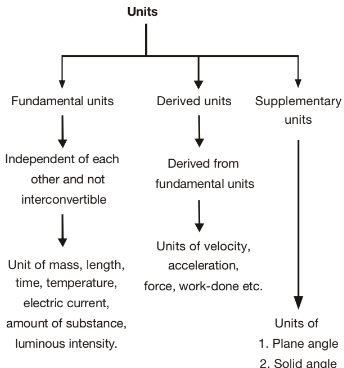
Besides the above 7 fundamental units, 2 supplementary units are also defined:
- Radian (rad) for plane angle
- Steradian (sr) for solid angle
Choice of a Standard Unit
The unit chosen should meet the following essential requirements: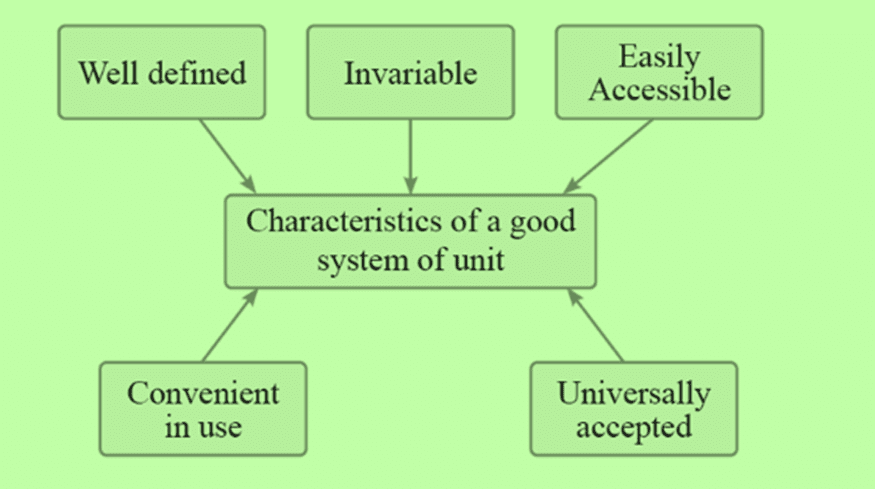
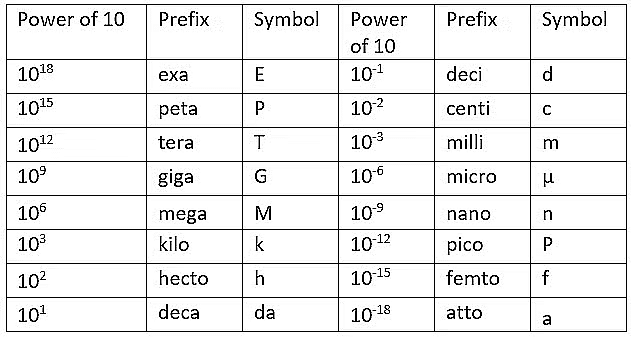
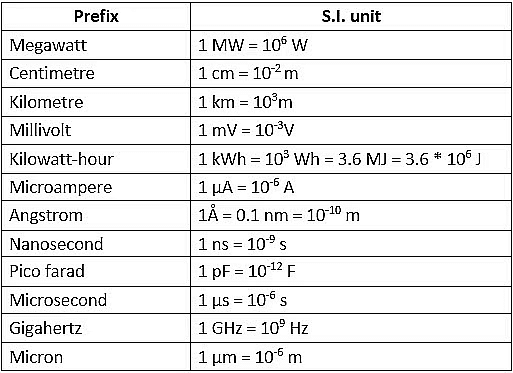
S.I. Prefixes
- The magnitudes of physical quantities vary over a wide range. The General Conference on Weight and Measures recommended standard prefixes for SI units to denote multiples and submultiples.
General Guidelines for Using Symbols
- Symbols for units of physical quantities are printed/written in Roman (upright type), and not in italics.
Example: 1N is correct, but 1N is incorrect. - Units are never written with capital initial letters even if named after a scientist.
Example: SI unit of force is newton (correct) Newton (incorrect). - The symbol for a unit named after a scientist is a capital letter. But for other units, the symbol is NOT a capital letter. Example :
- Symbols for units do not contain any final full stop at the end of the recommended letter and remain unaltered in the plural, using only the singular form of the unit.
Example:
The use of slash (/) is recommended only for indicating a division of one letter unit symbol by another unit symbol. Not more than one slash is used. Example:
Prefix symbols are printed in Roman (upright) type without spacing between the prefix and the unit symbol. Thus certain approved prefixes written very close to the unit symbol are used to indicate decimal fractions or multiples of an SI unit when it is inconveniently small or large. Example:
The unit 'fermi', equal to a femtometre or 10-15 m has been used as the convenient length unit in nuclear studies.
When a prefix is placed before the symbol of a unit, the combination of prefix and symbol is considered as a new symbol, for the unit, which can be raised to a positive or negative power without using brackets. These can be combined with other unit symbols to form a compound unit. Example:

A prefix is never used alone. It is always attached to a unit symbol and written or fixed before the unit symbol.
Example: 103/m3 = 1000/m3 or 1000 m-3, but not k/m3 or k m-3.The prefix symbol is written very close to the unit symbol without spacing between them, while unit symbols are written separately with spacing with units multiplied together. Example:
The use of double prefixes is avoided when single prefixes are available. Example:
A combination of units and symbols for the unit should be avoided when expressing a physical quantity with two or more units. Example :

Some Special Types of Units
- Micron (1μ) = 10-6 m (length)
- Angstrom (1 Å) = 10-8 cm = 10-10m (length)
- Fermi (1 f) = 10-13 cm = 10-15 m (length)
- Inch = 2.54 cm (length)
- Mile = 5280 feet = 1.609 km (length)
- Atmosphere = 105 N/m2 = 76 torr = 76 mm of Hg pressure (pressure)
- Litre = 10-3 m3 = 1000 cm3 (volume)
- Carat = 0.0002 kg (weight)
- Pound (Ib) = 0.4536 kg (weight)
Order of Magnitude
The order of magnitude tells us about the largeness or smallness of a physical quantity.
To find the order of magnitude the value of the physical quantity is expressed as a × 10b where 1 ≤ a < 10 and b is a positive or a negative integer. The exponent of 10, here it is b, is called of the order of magnitude.
For example:
- The radius of the Earth is 6.4 x 106m. If we take 6.4 as 10 then the order of magnitude of the radius of Earth is 107m.
- If the height of a girl is 1.7 m = 1.7 x 100m then the order of magnitude of the height of the girl is zero.
Example: What is the order of magnitude of 0.000520 kg?
Sol: 0.000520 kg = 5.2 x 10-4
As 5.2 > 5 so, 5.2 is nearly 10
= 10 x 10-4 = 10-3
So the order of magnitude is -3.
Classification of Physical Quantities
- Physical quantities can be grouped in different ways to help us understand their properties and how they relate to each other.
- Two common ways to classify these quantities are:
- Directional properties - This refers to how the quantities behave in terms of direction.
- Dependency - This indicates whether these quantities rely on other quantities.
- By looking at both the direction and the dependencies of physical quantities, we can learn more about how they act and their basic nature in the field of physics.
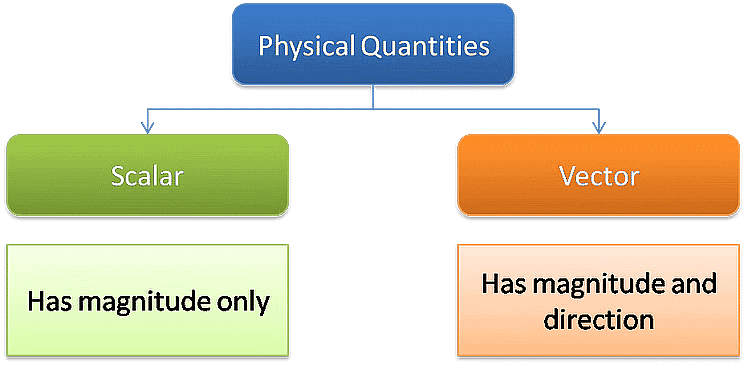
1. Based on their Directional Properties
Based on their directional properties, physical quantities can be classified into two categories:
(a) scalar quantities
(b) vector quantities.
 Classification based on Directional Properties
Classification based on Directional Properties
(a) Scalars: The physical quantities which have only magnitude but no direction are called scalar quantities. They are described solely by their numerical value or size.
Examples: Mass, temperature, energy, time, speed, and distance.
(b) Vectors: The physical quantities which have both magnitude and direction and obey the laws of vector algebra are called vector quantities. They require both numerical value and a specified direction to be fully described.
Examples: Displacement, velocity, acceleration, force, momentum, and electric field.
2. Based on their Dependency
Based on their dependency, physical quantities can be classified into three categories:
 Types of Physical Quantities
Types of Physical Quantities
(a) Fundamental Quantity
Although the number of physical quantities we measure is very large, we need only a limited number of units to express all the physical quantities since they are interrelated.
 Fundamental Physical Quantities
Fundamental Physical Quantities
Certain physical quantities have been chosen arbitrarily, and their units are used for expressing all the physical quantities. Such quantities are known as Fundamental Quantities (such as length, time, and mass in mechanics)
All other quantities may be expressed in terms of fundamental quantities.
These quantities are independent and cannot be expressed in terms of one another.
(b) Derived Quantity
Physical quantities that can be expressed as a combination of base quantities are called derived quantities. They can be infinite in number.
Example: Speed, velocity, acceleration, force, momentum, pressure, energy, etc.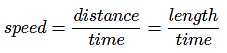
Derived Quantities
(c) Supplementary Quantity
There are two supplementary quantities in addition to the seven fundamental physical quantities that are defined in the International System of Units (S.I).
(i) Plane Angle:
Plane Angle is defined as the amount of rotation about the point of intersection of two lines that is required to make them overlap one another. The S.I. unit is radian.
θ= l/r, where =angle in radian ; l = length of arc and r=radius
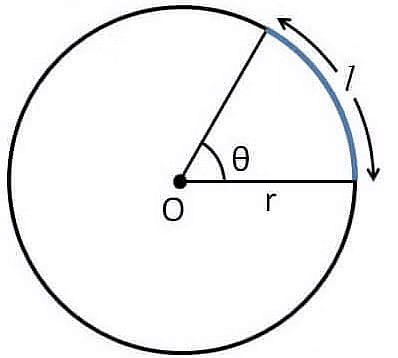 Plane Angle
Plane Angle
The degree is another unit used to measure plane angle. We can easily convert radian to degree and vice-versa.
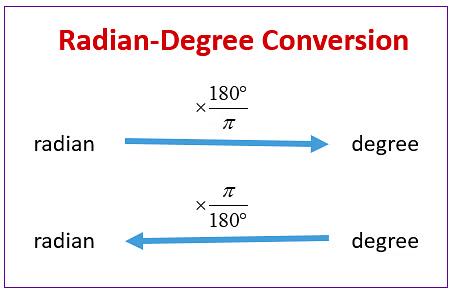 Radian to Degree Conversion
Radian to Degree Conversion
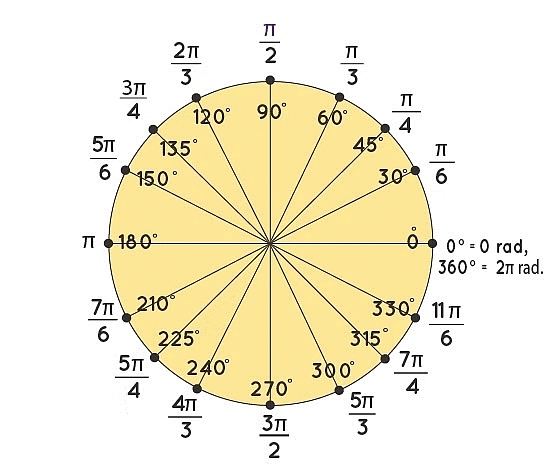 Commonly used Values
Commonly used Values
(ii) Solid Angle:
A solid angle is a cone subtended by a surface on the center of the sphere of which the surface is a part. It is defined by the ratio of the area of the surface to the square of the radius. It is measured in Steradian (sd).
 Solid Angle
Solid Angle
In the diagram, the area S of the sphere subtends a solid angle, Ω = S/r2
Dimensions of a Physical Quantity
Dimensions of a Physical Quantity
Dimensions are the powers to which fundamental units are raised to express the derived units of a quantity.
- If one knows the unit of any physical quantity, the dimension of the physical quantity can be easily written.
- We can express the dimensions of derived physical quantities in terms of the fundamental ones.
- Refer to the table below for a few examples :
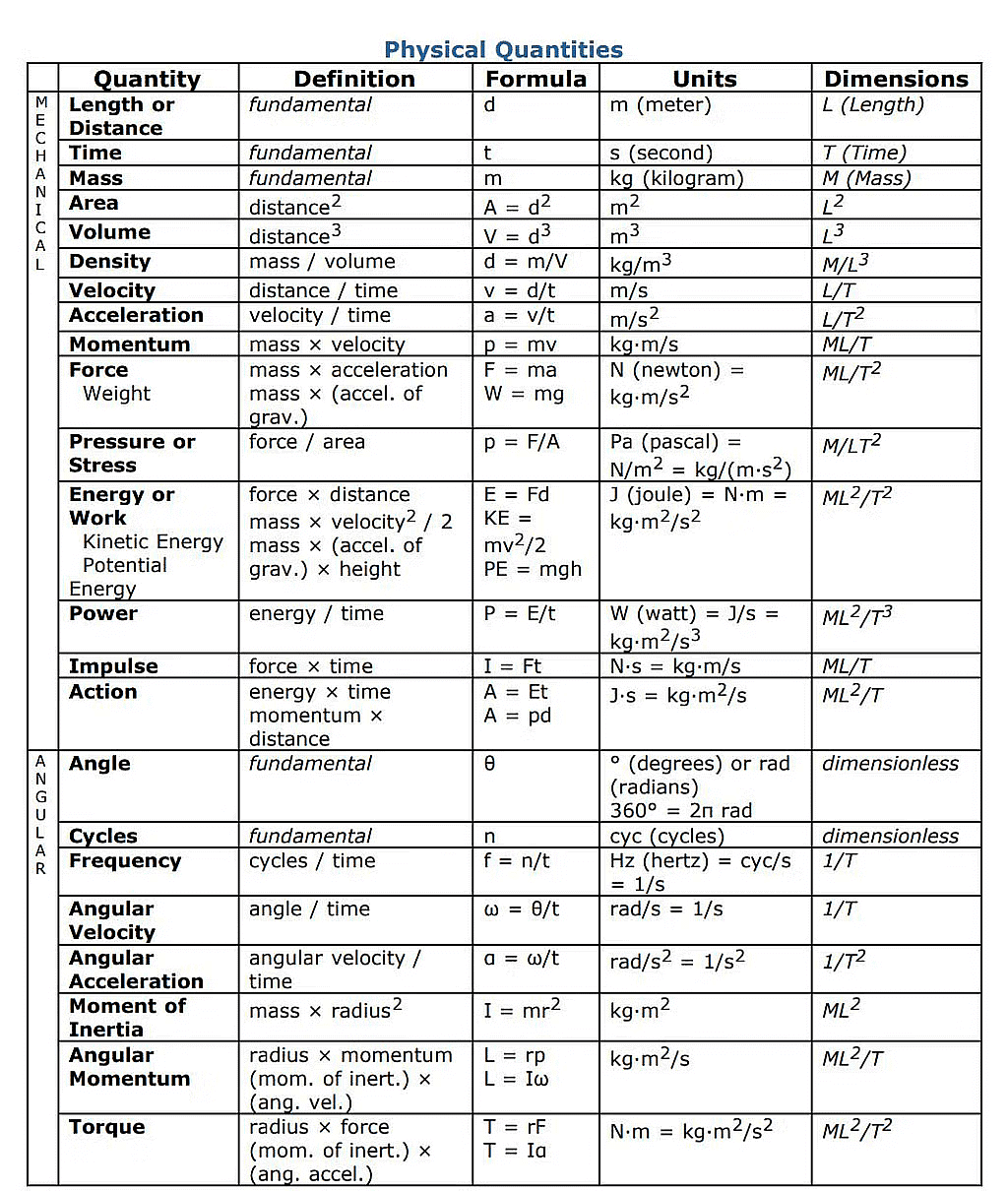 Commonly used derived units
Commonly used derived units
Apart from the above physical quantities, we can frame numerous dimensions of physical quantities. There are some constants in physics whose dimensions are of utmost importance :

Important :
- Two supplementary physical quantities i.e. angle and solid angle have units, but they are dimensionless.
- All the ratios involving the same physical quantities, like, strain and refractive index are both unitless and dimensionless.
- There is no such physical quantity that is unitless but has some dimension.
Dimensional Analysis
The basic concept of dimension is that we can add and subtract only quantities with the same dimensions. Similarly, two physical quantities can be equal only if they have the same dimensions. Dimensional analysis is essential because it keeps the units the same, helping us perform mathematical calculations smoothly.
Uses of Dimensional Analysis
1. To check the correctness of a physical equation.
2. To derive the relation between different physical quantities involved in a physical phenomenon.
3. To change from one system of units to another.
To read more about dimensional analysis and its applications, click here.
Significant Figures and Rounding off
Significant figures play an important role in all mathematics-based sciences. Significant Figures are the digits in your number that were measured plus one estimated digit. Significant Figures Rules:
1. All nonzero digits are significant.
2. Zeros between significant digits are significant.
3. Zeros to the left of non-zero digits are not significant.
4. Zeroes at the end of a number are significant only if they are to the right of the decimal point.
To read more about significant figures, click here.
Rounding Rules:
1. If the number ends in something greater than 5, then you round up.
2. If the number ends in something less than 5, then you round down.
3. (Round Half to Even Rule) If the number ends in a perfect 5 (in other words all or no zeros after the five), you round to the even number.
Addition and Subtraction: Round to the smallest number to the right of the decimal.
Multiplication and Division: Round to the number that has the least number of significant digits from the measured or given values.
Summary
- all trigonometric ratio is [M0L0T0]
- x in ex is [M0L0T0]
- ex is [M0L0T0]
- x in log x is [M0L0T0]
- log x is [M0L0T0]
6. The number of significant figures depends upon the least count of the instrument.
7. The number of significant figures does not depend on the units chosen.
|
95 videos|367 docs|98 tests
|
FAQs on Introduction to Units & Measurements - Physics Class 11 - NEET
| 1. What are physical quantities and how are they classified? |  |
| 2. What is the significance of the system of units in measurements? |  |
| 3. How do you determine the dimensions of a physical quantity? |  |
| 4. What is dimensional analysis and its applications? |  |
| 5. How do significant figures impact measurements and calculations? |  |