Square and Cube Roots: Shortcuts & Tricks | Quantitative Techniques for CLAT PDF Download
Tricks to Find Square Roots
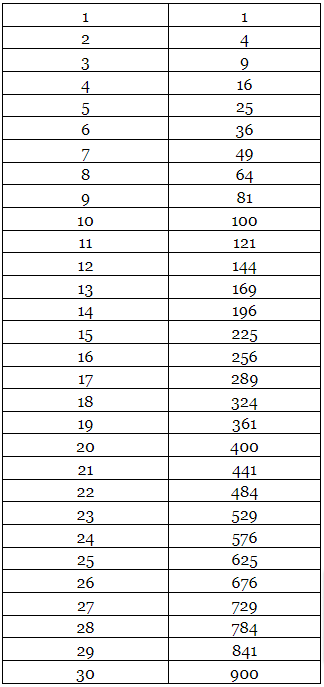
Before learning the trick to solve the square roots and cube roots. One must remember the squares up to 30 and cubes up to 15 (at least).
Squares from 1 to 30
Trick to find Perfect Square Roots
Learn above squares before applying this trick.
Now lets observe the pattern of the squares from 1 to 9.
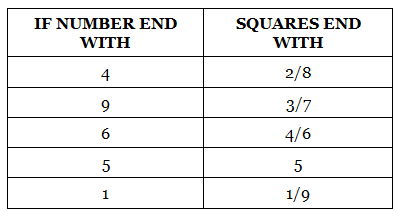
Keeping in mind the above pattern, now see how we can find the square of numbers.
Example: _/2304 = ?
Sol: First see the last two digits of the number of which we have to find the square root.
Here the last two digits of the number are 04. So we can see from the above table that square root will end with either 2 or 8.
Cross the last two digits after this step.
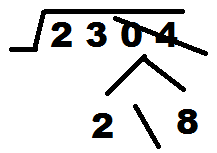
Now check the remaining number. Here the remaining number is 23. Take the perfect square less than this number i.e. before 23. We all know that 16 is the perfect square less than 23 and 16 is the square of 4. So 4 will be the first number of square root of 2304.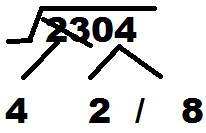
Now the question arises whether 42 will be the square root or 48.
There are two ways to identify this:
1st Way
Take the range in which the options are coming
Here the range is 40-50
402 = 1600
502 = 2500
2304 is near to 2500,
So 48 will be the answer.
2nd Way
Take the square of the number (common value) which ends with 5 ( as it is easy to find squares of number ending wit 5 ) and lies between 42 and 48 i.e. take square of 45.
452 = 2025
2304 > 2025
So, number more than 45 will be the answer, So 48 will be the answer.
Ans: = 48
Trick to find Imperfect Square
Generally Approximation questions contains imperfect squares in their questions. So lets discuss the tricks to solve the imperfect squares.
Example: _/ 9000
Consider the range in which the given number lies. Then take the difference from the lowest number of the range. Divide the resultant number with the number of lowest range multiplied by 2.Add both results and that will be the answer.
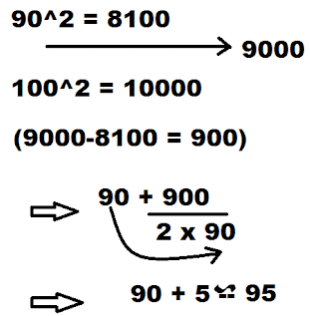
Range in which the given number lies.
Difference of number and lowest range,
90 will be surely part of answer as square of 90 is 8100 which is less than 9000. Now take the difference as numerator and divide it by the other part i.e. 90*2 (Always multiply the denominator by 2)
Tricks to Find Cube Roots
Cubes from 1 to 15
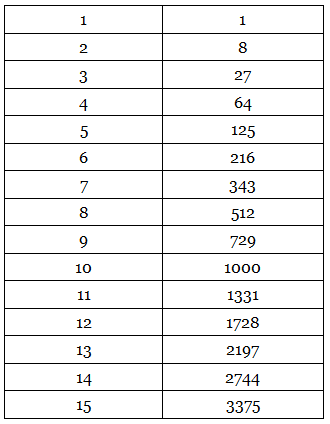
Learn above cubes before applying this trick.
Now, observe the pattern of the cubes from 1 to 9.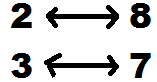
Trick to Find Perfect Cube Roots
Example: 3/17576
First see the last three digits of the number of which we have to find the cube root.
Here the last three digits of the number are 576. So we can see from the above table that cube root will end with 6.
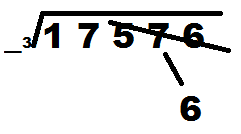
Cross the last digits of the number after this step.
Now check the remaining number i.e. 17. Perfect cube before 17 is 8 and 8 is cube of 2. So 2 will be the first digit of cube root.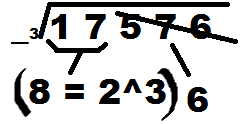
Ans: 26
Tricks to Find Imperfect Cubes
Generally Approximation questions contains imperfect cubes in their questions. So lets discuss the tricks to solve the imperfect cubes.
Example : _3/80000
Consider the range in which the given number lies. Then take the difference of the lowest number of the range and given number.
The range in which 8000 lies is 403 - 503
 Always multiply the result with 10
Always multiply the result with 10
= 40 + 2.5
= 42.5 ( approx)
|
49 videos|179 docs|73 tests
|
FAQs on Square and Cube Roots: Shortcuts & Tricks - Quantitative Techniques for CLAT
| 1. How can I find the square root of a perfect square? |  |
| 2. How can I find the square root of an imperfect square? |  |
| 3. What is a trick to find cube roots? |  |
| 4. How can I find the perfect cube root of a number? |  |
| 5. How can I find the cube root of an imperfect cube? |  |
















