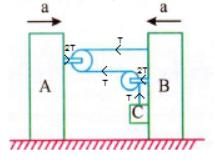
All questions of Force and Motion for Grade 9 Exam
Two bodies of mass 4 kg and 6 kg are attached to the ends of a string passing over a pulley. A 4 kg mass is attached to the table top by another string. The tension in this string T1 is equal to (g = 10 m/s2) 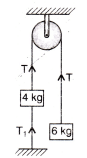
- a)20 N
- b)25 N
- c)15 N
- d)10 N
Correct answer is option 'A'. Can you explain this answer?
Two bodies of mass 4 kg and 6 kg are attached to the ends of a string passing over a pulley. A 4 kg mass is attached to the table top by another string. The tension in this string T1 is equal to (g = 10 m/s2)
a)
20 N
b)
25 N
c)
15 N
d)
10 N

|
Mohit Rajpoot answered |
A block sliding along inclined plane as shown in figure. If the acceleration of chamber is ‘a’ as shown in the figure. The time required to cover a distance L along inclined plane is 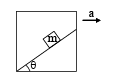
- a)
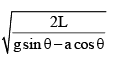
- b)
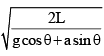
- c)
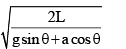
- d)

Correct answer is option 'C'. Can you explain this answer?
A block sliding along inclined plane as shown in figure. If the acceleration of chamber is ‘a’ as shown in the figure. The time required to cover a distance L along inclined plane is
a)
b)
c)
d)
|
|
Neha Sharma answered |
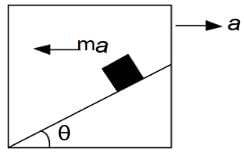
Applying pseudo force ma along the left direction of the block.
The net acceleration along the incline will be aeffective=acosθ+gsinθ
The time required will be L=0×t+½ aeffectivet2
⇒ √ 2L/ aeffective
⇒√ 2L /acosθ+gsinθ
Concept of pseudo force is valid only in- a)inertial frame
- b)Non-inertial frame
- c)can be inertial or non-inertial frame
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
Concept of pseudo force is valid only in
a)
inertial frame
b)
Non-inertial frame
c)
can be inertial or non-inertial frame
d)
None of these
|
|
Rohit Shah answered |
This is because newton's laws are valid only for inertial frames. Analysis from an inertial frame isn't possible using those laws, to put it simple.
Let us assume a glass lift is going up with an acceleration 'a'. with respect to the ground. Clearly, this is a non-inertial frame as it has an acceleration. Man 'A' is inside the lift and wants to analyze the motion of the lift, but he cannot, as the newton's laws are not valid. So he takes his phone and calls Man 'B', who stands outside on the ground (in an inertial frame). This fellow watches Man 'A' go up with acceleration 'a'. Forces acting on Man 'A' are:
1. Weight, mg
2. Normal reaction offered by the lift, N
Thus, taking upward direction as positive and using Newton's Law, he writes the equation,
N - mg = ma, or
N = mg+ma
He tells "N=mg+ma" on phone to Man 'A'.
Now, Man 'A' looks around himself. According to himself, he is at rest. So, according to him, N = mg. Sadly, he knows this is not a correct analysis, as the newton's laws can't be applied!
The correct analysis, as received on phone, is N=mg+ma!
This is his eureka moment! He realizes that if he considers a "pseudo force" of magnitude 'ma' acting in opposite direction to acceleration of his frame, a correct analysis is possible!
This is why the concept of pseudo force is introduced, although it isn't necessary. You can always equate the net force in a direction equal to mass times acceleration from outside the non-inertial frame. However, if you want to do it from the non-inertial frame, the result can be interpreted in such a way, which suggests that the body is under rest, but an additional force (pseudo force) is acting.
What is the smallest radius of a circle at which a bicyclist can travel if his speed is 7 m/s and the coefficient of static friction between tyres and road is 0.25 - a)10 m
- b)20 m
- c)5 m
- d)15 m
Correct answer is option 'B'. Can you explain this answer?
What is the smallest radius of a circle at which a bicyclist can travel if his speed is 7 m/s and the coefficient of static friction between tyres and road is 0.25
a)
10 m
b)
20 m
c)
5 m
d)
15 m
|
|
Anjali Sharma answered |
Centripetal force = Frictional force
⇒ mv2/r=μmg
∴r=v2/μg
∴r=72/0.25×10
∴r=19.6 m≈20 m
⇒ mv2/r=μmg
∴r=v2/μg
∴r=72/0.25×10
∴r=19.6 m≈20 m
A block of mass 2 kg is placed on the floor. The coefficient of static friction is 0.4. If a force of 2.8 N is applied on the block parallel to floor, the force of friction between the block and floor is (Take g = 10 m/s2) - a)2.8 N
- b)8 N
- c)2 N
- d)zero
Correct answer is option 'A'. Can you explain this answer?
A block of mass 2 kg is placed on the floor. The coefficient of static friction is 0.4. If a force of 2.8 N is applied on the block parallel to floor, the force of friction between the block and floor is (Take g = 10 m/s2)
a)
2.8 N
b)
8 N
c)
2 N
d)
zero
|
|
Geetika Shah answered |
Weight of the block is 20N thus maximum friction that can act is 0.4 x 20 = 8N
But as the external force acting, F = 2.8N < 8N,
We get f = F = 2.8N
But as the external force acting, F = 2.8N < 8N,
We get f = F = 2.8N
The frictional force between two surfaces is independent of- a)nature of surface
- b)mass of the body
- c) area of contact
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
The frictional force between two surfaces is independent of
a)
nature of surface
b)
mass of the body
c)
area of contact
d)
None of these
|
|
Krishna Iyer answered |
The frictional force between two surfaces 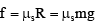
where μs depends on the nature of surface and their materials. Thus, frictional force is independent of area of contact of the surfaces.
Two bodies of mass 6 kg and 4 kg are tied to a string as shown in the adjoining figure. If the table is smooth and pulley frictionless, then acceleration of mass 6 kg will be (g = 10 m/s2)
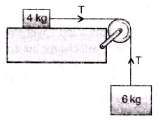
- a)60 m/s2
- b)40 m/s2
- c)6 m/s2
- d)4 m/s2
Correct answer is option 'C'. Can you explain this answer?
Two bodies of mass 6 kg and 4 kg are tied to a string as shown in the adjoining figure. If the table is smooth and pulley frictionless, then acceleration of mass 6 kg will be (g = 10 m/s2)
a)
60 m/s2
b)
40 m/s2
c)
6 m/s2
d)
4 m/s2
|
|
Ananya Singh answered |

A ball of mass 0.5 kg is attached to the end of a string having length 0.5 m. The hall is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is 324 N. The maximum possible value of angular velocity of ball in (rad/s) - a)9
- b)18
- c)27
- d)36
Correct answer is option 'D'. Can you explain this answer?
A ball of mass 0.5 kg is attached to the end of a string having length 0.5 m. The hall is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is 324 N. The maximum possible value of angular velocity of ball in (rad/s)
a)
9
b)
18
c)
27
d)
36
|
|
Pooja Kulkarni answered |
T sin θ = mrω2; r = l sin θ
A small coin is placed on a horizontal turn table. The turn table is observed to make three revolutions in 3.14 sec. What is the coefficient of static friction between the coin and turn table if the coin is observed to slide off the turn table when it is greater than 10 cm from the centre of the turn table - a)0.4
- b)0.04
- c)4
- d)0.004
Correct answer is option 'B'. Can you explain this answer?
A small coin is placed on a horizontal turn table. The turn table is observed to make three revolutions in 3.14 sec. What is the coefficient of static friction between the coin and turn table if the coin is observed to slide off the turn table when it is greater than 10 cm from the centre of the turn table
a)
0.4
b)
0.04
c)
4
d)
0.004
|
|
Om Desai answered |
F = ma
so a = 250/30
a = 8.34
now the result is 4mt/secsqure
so reduction is 4.34
friction force will b 4.34 ×30
F = 130.2 N
Frictional force between two bodies - a)Adds the motion between the bodies
- b)Destroys the relative motion between the bodies
- c)Sometimes helps and sometimes opposes the motion
- d)Increases the relative velocity between the bodies
Correct answer is option 'C'. Can you explain this answer?
Frictional force between two bodies
a)
Adds the motion between the bodies
b)
Destroys the relative motion between the bodies
c)
Sometimes helps and sometimes opposes the motion
d)
Increases the relative velocity between the bodies
|
|
Raghav Bansal answered |
Friction does not always oppose motion. For eg when a car is accelerating forward , the tyres push against the road in a backward direction. Friction pushes itself in forward and the car also pushes forward. Thus friction and motion are in the same direction.
Similarly when a runner accelerates forward the shoe pushes backward, friction pushes forward and runner pushes forward. Thus both are in same direction
Hence force of friction does not always oppose motion or the tendency of motion.
Similarly when a runner accelerates forward the shoe pushes backward, friction pushes forward and runner pushes forward. Thus both are in same direction
Hence force of friction does not always oppose motion or the tendency of motion.
Two masses of 1 kg and 5 kg are attached to the ends of a massless string passing over a pulley of negligible weight. The pulley itself is attached to a light spring balance as shown in the figure. The masses start moving during this interval, the reading of spring balance will be 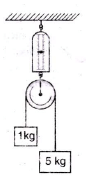
- a)more than 6 kg
- b)less than 6 kg
- c) equal to 6 kg
- d)none of the above
Correct answer is option 'B'. Can you explain this answer?
Two masses of 1 kg and 5 kg are attached to the ends of a massless string passing over a pulley of negligible weight. The pulley itself is attached to a light spring balance as shown in the figure. The masses start moving during this interval, the reading of spring balance will be
a)
more than 6 kg
b)
less than 6 kg
c)
equal to 6 kg
d)
none of the above
|
|
Suresh Reddy answered |
Applying the 2nd law of motion,
Equating all forces on the string carrying the 2 blocks we get T = 5g/3
The tension in spring balance = 2T
So, the reading is the mass = T/g = 10/3 Kg < 6Kg
Equating all forces on the string carrying the 2 blocks we get T = 5g/3
The tension in spring balance = 2T
So, the reading is the mass = T/g = 10/3 Kg < 6Kg
A heavy block of mass M is slowly placed on a conveyor belt moving with a speed v. The coefficient of friction between the block and the belt is μ. Through what distance will the block slide on the belt?- a)v/ug
- b)v2/ug
- c)v/2ug
- d)v2/2ug
Correct answer is option 'D'. Can you explain this answer?
A heavy block of mass M is slowly placed on a conveyor belt moving with a speed v. The coefficient of friction between the block and the belt is μ. Through what distance will the block slide on the belt?
a)
v/ug
b)
v2/ug
c)
v/2ug
d)
v2/2ug
|
|
Simran Chauhan answered |
Frictional force on the block = μMg
It will be causing acceleration a =μMg/M = μg
The block slide on the ball till its velocity becomes ‘v’ given by the equation
The car A is used to pull a load B with the pulley arrangement shown. If A has a forward velocity v determine an expression for the upward velocity vB of the load in terms of vA and θ.θ is angle between string and horizontal 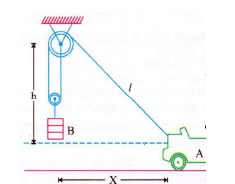
- a) 1/2 VA cosθ
- b) VA sinθ
- c)VA cosθ
- d) 1/2 VA sinθ
Correct answer is option 'A'. Can you explain this answer?
The car A is used to pull a load B with the pulley arrangement shown. If A has a forward velocity v determine an expression for the upward velocity vB of the load in terms of vA and θ.θ is angle between string and horizontal
a)
1/2 VA cosθ
b)
VA sinθ
c)
VA cosθ
d)
1/2 VA sinθ

|
Knowledge Hub answered |
Let θ angle between string and horizontal, T is tension in string
A block has been placed on an inclined plane. The slope angle θ of the plane is such that the block slides down the plane at a constant speed. The coefficient of kinetic friction is equal to - a)sinθ
- b)cos θ
- c)g
- d)tan θ
Correct answer is option 'D'. Can you explain this answer?
A block has been placed on an inclined plane. The slope angle θ of the plane is such that the block slides down the plane at a constant speed. The coefficient of kinetic friction is equal to
a)
sinθ
b)
cos θ
c)
g
d)
tan θ
|
|
Rajat Kapoor answered |
When the block slides down the plane with a constant speed, then the inclination of the plane is equal to angle of repose (q).
Coeff. of friction = tan of the angle of repose = tan q.
A light string fixed at one end to a clamp on ground passes over a fixed pulley and hangs at the other side. It makes an angle of 30o with the ground. A monkey of mass 5 kg climbs up the rope. The clamp can tolerate a vertical force of 40 N only. The maximum acceleration in upward direction with which the monkey can climb safely is (neglect friction and take g = 10 m/s2)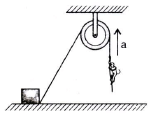
- a)2 m/s2
- b)4 m/S2
- c)6 m/s2
- d)8 m/s2
Correct answer is option 'C'. Can you explain this answer?
A light string fixed at one end to a clamp on ground passes over a fixed pulley and hangs at the other side. It makes an angle of 30o with the ground. A monkey of mass 5 kg climbs up the rope. The clamp can tolerate a vertical force of 40 N only. The maximum acceleration in upward direction with which the monkey can climb safely is (neglect friction and take g = 10 m/s2)
a)
2 m/s2
b)
4 m/S2
c)
6 m/s2
d)
8 m/s2

|
Lohit Matani answered |
Let T be the tension in the string.
The upward force exerted on the clamp = T sin 30o = T/2
Given: (T/2) = 40 N or T = 80 N
If ‘a’ is the acceleration of the monkey in upward direction,
A boy of mass 40 kg is climbing a vertical pole at a constant speed. If the coefficient of friction between his palms and the pole is 0.8 and g = 10 m/s2 the horizontal force that he is applying on the pole is- a)250 N
- b)200 N
- c)500 N
- d)50 N
Correct answer is option 'C'. Can you explain this answer?
A boy of mass 40 kg is climbing a vertical pole at a constant speed. If the coefficient of friction between his palms and the pole is 0.8 and g = 10 m/s2 the horizontal force that he is applying on the pole is
a)
250 N
b)
200 N
c)
500 N
d)
50 N
|
|
Lavanya Menon answered |
Here, μ= 0. 8
Let F be horizontal force that the boy is applying on the pole.
The various forces are acting on the boy as shown in the below figure.
Frictional force.
The various forces are acting on the boy as shown in the below figure.
Frictional force.
In the pulley-block arrangement shown in figure. Find the relation between acceleration of block A and B. 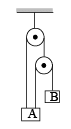
- a)aB = -3aA
- b)aB = -aA
- c)aB = -2aA
- d)aB = -4aA
Correct answer is option 'A'. Can you explain this answer?
In the pulley-block arrangement shown in figure. Find the relation between acceleration of block A and B.
a)
aB = -3aA
b)
aB = -aA
c)
aB = -2aA
d)
aB = -4aA
|
|
Akanksha Reddy answered |
x1 + x2 = l1
Differentiating with respect to time, we get v1 + v3 = 0
Again differentiating w.r.t. time,
A block rests on a rough inclined plane making an angle of 30o with the horizontal. The coefficient of static friction between the block and the plane is 0.8. If the frictional force on the block is 10 N, the mass of the block (in kg) is (Take g = 10 m/s2) - a)2.5
- b)4.0
- c)1.6
- d)2.0
Correct answer is option 'D'. Can you explain this answer?
A block rests on a rough inclined plane making an angle of 30o with the horizontal. The coefficient of static friction between the block and the plane is 0.8. If the frictional force on the block is 10 N, the mass of the block (in kg) is (Take g = 10 m/s2)
a)
2.5
b)
4.0
c)
1.6
d)
2.0

|
Anisha Chauhan answered |
In figure, coefficient of friction between m1 and m2 is m and that between m1 and the wall is zero. A force F is pressing the system against the wall. Minimum value of force required to hold the system in equilibrium is 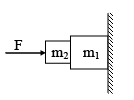
- a)mm1g
- b)mm2g
- c)m(m1 + m2)g
- d)system cannot be held in equilibrium
Correct answer is option 'D'. Can you explain this answer?
In figure, coefficient of friction between m1 and m2 is m and that between m1 and the wall is zero. A force F is pressing the system against the wall. Minimum value of force required to hold the system in equilibrium is
a)
mm1g
b)
mm2g
c)
m(m1 + m2)g
d)
system cannot be held in equilibrium

|
Priyanka Roy answered |
There is no force which can balance the weight of m1.
A body of mass 60 kg is dragged with just enough force to start moving on a rough surface with coefficients of static and kinetic frictions 0.5 and 0.4 respectively. On applying the same force, what is the acceleration? - a)0.98 m/s2
- b)9.8 m/s2
- c)0.54 m/s2
- d)5.292 m/s2
Correct answer is option 'A'. Can you explain this answer?
A body of mass 60 kg is dragged with just enough force to start moving on a rough surface with coefficients of static and kinetic frictions 0.5 and 0.4 respectively. On applying the same force, what is the acceleration?
a)
0.98 m/s2
b)
9.8 m/s2
c)
0.54 m/s2
d)
5.292 m/s2
|
|
Shreya Gupta answered |
maximum static friction that can act on the body is Umg = 0.5*60*9.8 = 294 N
now since the force is just above 300 N, the body will translate and the type of friction now will be kinetic instead of static. Hence the net acceleration is 294-0.4*60*9.8/60 = 0.98 m/s^2 Ans.
Three masses of 1 kg, 6 kg and 3 kg are connected to each other with threads and are placed on a table a as shown in the figure. What is the acceleration with which the system is moving (Take g = 10 m/s2)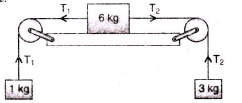
- a)zer
- b)1 m/s2
- c)2 m/s2
- d)3 m/s2
Correct answer is option 'C'. Can you explain this answer?
Three masses of 1 kg, 6 kg and 3 kg are connected to each other with threads and are placed on a table a as shown in the figure. What is the acceleration with which the system is moving (Take g = 10 m/s2)
a)
zer
b)
1 m/s2
c)
2 m/s2
d)
3 m/s2
|
|
Nayanika Chakraborty answered |
A block is placed on a rough surface and an external horizontal force F is applied on it. The force of friction ‘f’ exerted by the floor on the block is measured for different values of F. The graph between F and f is - a)straight line parallel to F-axis
- b)straight line inclined at 45o
- c)straight line inclined at 45o for small values of F and straight line parallel to F-axis for large F
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
A block is placed on a rough surface and an external horizontal force F is applied on it. The force of friction ‘f’ exerted by the floor on the block is measured for different values of F. The graph between F and f is
a)
straight line parallel to F-axis
b)
straight line inclined at 45o
c)
straight line inclined at 45o for small values of F and straight line parallel to F-axis for large F
d)
none of these

|
Bhargavi Chopra answered |
Theoretical
A block of weight 100 N is pushed by a force F on a horizontal rough plane moves with an acceleration 1 m/s2, when force is doubled its acceleration becomes 10 m/s2. The coefficient of friction is (g = 10 m/s2) - a)0.4
- b)0.6
- c)0.5
- d)0.8
Correct answer is option 'D'. Can you explain this answer?
A block of weight 100 N is pushed by a force F on a horizontal rough plane moves with an acceleration 1 m/s2, when force is doubled its acceleration becomes 10 m/s2. The coefficient of friction is (g = 10 m/s2)
a)
0.4
b)
0.6
c)
0.5
d)
0.8

|
Aniket Basu answered |
The acceleration that is produced by a 15N force in a mass of 8 kg will be equal to
- a)1.5 ms−2
- b)1.875 ms−2
- c)2.35 ms−2
- d)2 ms−2
Correct answer is option 'B'. Can you explain this answer?
The acceleration that is produced by a 15N force in a mass of 8 kg will be equal to
a)
1.5 ms−2
b)
1.875 ms−2
c)
2.35 ms−2
d)
2 ms−2
|
|
Akshara Gupta answered |
As we know that F = ma
15 = 8a
=> 15/8 = a
a = 1.875 ms-2
15 = 8a
=> 15/8 = a
a = 1.875 ms-2
A block of mass 4 kg is suspended through two light spring balances A and B. Then A and B will read respectively 
- a)4 kg and zero kg
- b)zero kg and 4 kg
- c)4 kg and 4 kg
- d)2 kg and 2 kg
Correct answer is option 'C'. Can you explain this answer?
A block of mass 4 kg is suspended through two light spring balances A and B. Then A and B will read respectively
a)
4 kg and zero kg
b)
zero kg and 4 kg
c)
4 kg and 4 kg
d)
2 kg and 2 kg

|
EduRev Humanities answered |
Tension is uniformly transmitted if the springs are massless.
A trolley T of mass 5 kg on a horizontal smooth surface is pulled by a load of 2 kg through a uniform rope ABC of length 2 m and mass 1 kg. As the load falls from BC = 0 to BC = 2 m, its acceleration (in m/s2) changes from
- a)20/6 to 30/5
- b)20/8 to 30/8
- c)20/5 to 30/6
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
A trolley T of mass 5 kg on a horizontal smooth surface is pulled by a load of 2 kg through a uniform rope ABC of length 2 m and mass 1 kg. As the load falls from BC = 0 to BC = 2 m, its acceleration (in m/s2) changes from
a)
20/6 to 30/5
b)
20/8 to 30/8
c)
20/5 to 30/6
d)
none of these
|
|
Nabanita Chavan answered |
Initial force = load x g = 2 x 10 = 20 N
∴ initial acceleration = Force/Mass = 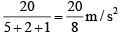
Final force = (load + mass of the thread) x g = ( 2 + 1 ) x 10 = 30N
∴ Final acceleration = (30/8) m/s2
A body moves along a circular path of radius 5 m. The coefficient of friction between the surface of the path and the body is 0.5. The angular velocity in rad/s with which the body should move so that it does not leave the path is (g = 10 m/s2) - a)4
- b)3
- c)2
- d)1
Correct answer is option 'D'. Can you explain this answer?
A body moves along a circular path of radius 5 m. The coefficient of friction between the surface of the path and the body is 0.5. The angular velocity in rad/s with which the body should move so that it does not leave the path is (g = 10 m/s2)
a)
4
b)
3
c)
2
d)
1

|
Athul Yadav answered |
The limiting friction between two surface does not depend - a)on the nature of two surfaces
- b)on normal reaction
- c)on the weight of the body
- d)on volume of the body
Correct answer is option 'D'. Can you explain this answer?
The limiting friction between two surface does not depend
a)
on the nature of two surfaces
b)
on normal reaction
c)
on the weight of the body
d)
on volume of the body
|
|
Anjali Iyer answered |
Limiting friction is the maximum value of static friction which operates when a body is just going to start sliding over the surface of another body. It depends upon the nature of the surface but independent of the area of surface, provided the normal reaction remains unaltered.
A uniform rope of length l lies on a table. If the coefficient of friction is μ, then the maximum length l1 of the part of this rope which can overhang from the edge of the table without sliding down is - a) 1/μ
- b) 1/μ+1
- c) μl/μ+1
- d) μl/μ-1
Correct answer is option 'C'. Can you explain this answer?
A uniform rope of length l lies on a table. If the coefficient of friction is μ, then the maximum length l1 of the part of this rope which can overhang from the edge of the table without sliding down is
a)
1/μ
b)
1/μ+1
c)
μl/μ+1
d)
μl/μ-1

|
Sarthak Verma answered |
Frictional force acting on the block is
- a)30 N
- b)20 N
- c)10 N
- d)zero
Correct answer is option 'A'. Can you explain this answer?
Frictional force acting on the block is
a)
30 N
b)
20 N
c)
10 N
d)
zero
|
|
Pooja Shah answered |
Net force = 50 - 20 = 30 N
Limiting friction on the body = u (static) × m × g = 0.6 × 10 × 10 = 60 N.
F = 30 N is less than the limiting friction so the body is static. So, a = 0.
Force of friction acting on the body is static friction, f = driving force = 30 N.
Limiting friction on the body = u (static) × m × g = 0.6 × 10 × 10 = 60 N.
F = 30 N is less than the limiting friction so the body is static. So, a = 0.
Force of friction acting on the body is static friction, f = driving force = 30 N.
The pulley arrangements shown in figure are identical, the mass of the rope being negligible. In case I, the mass m is lifted by attaching a mass 2m to the other end of the rope. In case II, the mass m is lifted by pulling the other end of the rope with a constant downward force, F = 2 mg, where g is acceleration due to gravity. The acceleration of mass m in case I is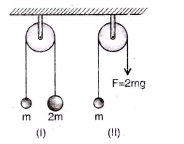
- a)zero
- b)more than that in case II
- c) less than that in case II
- d)equal to that in case II
Correct answer is option 'C'. Can you explain this answer?
The pulley arrangements shown in figure are identical, the mass of the rope being negligible. In case I, the mass m is lifted by attaching a mass 2m to the other end of the rope. In case II, the mass m is lifted by pulling the other end of the rope with a constant downward force, F = 2 mg, where g is acceleration due to gravity. The acceleration of mass m in case I is
a)
zero
b)
more than that in case II
c)
less than that in case II
d)
equal to that in case II

|
Ashwini Majumdar answered |
A body of mass 2 kg rests on a rough inclined plane making an angle 30o with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is- a) 9.8 N
- b)0.7 x 9.8 x √3 N
- c)9.8 x √3 N
- d)0.7 x 9.8 N
Correct answer is option 'A'. Can you explain this answer?
A body of mass 2 kg rests on a rough inclined plane making an angle 30o with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
a)
9.8 N
b)
0.7 x 9.8 x √3 N
c)
9.8 x √3 N
d)
0.7 x 9.8 N

|
Krish Ghoshal answered |
Understanding the Problem
A body of mass 2 kg is resting on a rough inclined plane at an angle of 30 degrees with the horizontal. The coefficient of static friction is given as 0.7. We need to calculate the frictional force acting on the block.
Forces Acting on the Block
- The weight of the block (W) can be calculated as:
- W = mass x gravity = 2 kg x 9.8 m/s² = 19.6 N
- The weight can be resolved into two components:
- Perpendicular to the incline: W⊥ = W * cos(30°)
- Parallel to the incline: W|| = W * sin(30°)
Calculating the Frictional Force
- The maximum static friction (Fs_max) can be calculated using the formula:
- Fs_max = μs * N, where μs is the coefficient of static friction and N is the normal force.
- The normal force (N) on the incline is equal to the perpendicular component of the weight:
- N = W⊥ = W * cos(30°) = 19.6 N * cos(30°) = 19.6 N * (√3/2) ≈ 16.97 N
- Now, substituting the values into the static friction formula:
- Fs_max = 0.7 * N = 0.7 * 16.97 N ≈ 11.88 N
Frictional Force on the Block
- Since the block is at rest, the frictional force will be equal to the force trying to move it down the incline, which is W||.
- W|| = W * sin(30°) = 19.6 N * 0.5 = 9.8 N
Thus, the frictional force acting on the block is equal to the force trying to move it, which is 9.8 N.
Conclusion
The correct answer is option 'A': 9.8 N. The frictional force balances the component of weight parallel to the incline, keeping the block at rest.
A body of mass 2 kg is resting on a rough inclined plane at an angle of 30 degrees with the horizontal. The coefficient of static friction is given as 0.7. We need to calculate the frictional force acting on the block.
Forces Acting on the Block
- The weight of the block (W) can be calculated as:
- W = mass x gravity = 2 kg x 9.8 m/s² = 19.6 N
- The weight can be resolved into two components:
- Perpendicular to the incline: W⊥ = W * cos(30°)
- Parallel to the incline: W|| = W * sin(30°)
Calculating the Frictional Force
- The maximum static friction (Fs_max) can be calculated using the formula:
- Fs_max = μs * N, where μs is the coefficient of static friction and N is the normal force.
- The normal force (N) on the incline is equal to the perpendicular component of the weight:
- N = W⊥ = W * cos(30°) = 19.6 N * cos(30°) = 19.6 N * (√3/2) ≈ 16.97 N
- Now, substituting the values into the static friction formula:
- Fs_max = 0.7 * N = 0.7 * 16.97 N ≈ 11.88 N
Frictional Force on the Block
- Since the block is at rest, the frictional force will be equal to the force trying to move it down the incline, which is W||.
- W|| = W * sin(30°) = 19.6 N * 0.5 = 9.8 N
Thus, the frictional force acting on the block is equal to the force trying to move it, which is 9.8 N.
Conclusion
The correct answer is option 'A': 9.8 N. The frictional force balances the component of weight parallel to the incline, keeping the block at rest.
A man walks over a rough surface, the angle between the force of friction and the instantaneous velocity of the person isa)pb)p/2c)p/4d)zeroCorrect answer is option 'D'. Can you explain this answer?

|
Sparsh Sen answered |
When a man walks on a rough surface, it is the frictional force which is responsible for motion, i.e, required angle between frictional force and instantaneous velocity is zero.
A body is moving with uniform velocity of 2 m/s on a rough level surface. The frictional force on it is 10 N. If the body moves with velocity 4 m/s, the force of friction will be - a)2.5 N
- b)5 N
- c)10 N
- d)20 N
Correct answer is option 'C'. Can you explain this answer?
A body is moving with uniform velocity of 2 m/s on a rough level surface. The frictional force on it is 10 N. If the body moves with velocity 4 m/s, the force of friction will be
a)
2.5 N
b)
5 N
c)
10 N
d)
20 N
|
|
Shivani Joshi answered |
Frictional Force on a Body Moving with Uniform Velocity
- When a body is moving with a uniform velocity on a rough level surface, the frictional force acting on it is equal to the product of the coefficient of friction (μ) and the normal force (N).
Frictional Force = μN
- In this case, the velocity of the body is given as 2 m/s and the frictional force is given as 10 N. We need to find the frictional force when the velocity of the body is 4 m/s.
Using the formula for frictional force, we have:
10 N = μN (equation 1)
- Now, let's consider the situation when the body moves with a velocity of 4 m/s. Since the velocity has increased, the frictional force will also increase.
- The normal force acting on the body remains the same, as the body is still on the same rough level surface. Therefore, the normal force can be considered constant.
- Let's assume the new frictional force is F (to be determined).
Using the formula for frictional force, we have:
F = μN (equation 2)
- We can compare equations 1 and 2 to find the relationship between the frictional force and the velocity of the body.
Since the normal force is constant, we can cancel it out from both equations:
10 N = μN
F = μN
- Now, let's compare the velocities:
2 m/s ≠ 4 m/s
- From this comparison, we can conclude that the frictional force is not directly proportional to the velocity of the body.
- Therefore, we cannot directly use the given frictional force of 10 N to find the frictional force when the velocity is 4 m/s.
- Hence, without any additional information or assumptions about the coefficient of friction, we cannot determine the exact value of the frictional force when the velocity of the body is 4 m/s.
- Therefore, the correct answer cannot be determined and none of the given options (a, b, c, d) are correct.
- When a body is moving with a uniform velocity on a rough level surface, the frictional force acting on it is equal to the product of the coefficient of friction (μ) and the normal force (N).
Frictional Force = μN
- In this case, the velocity of the body is given as 2 m/s and the frictional force is given as 10 N. We need to find the frictional force when the velocity of the body is 4 m/s.
Using the formula for frictional force, we have:
10 N = μN (equation 1)
- Now, let's consider the situation when the body moves with a velocity of 4 m/s. Since the velocity has increased, the frictional force will also increase.
- The normal force acting on the body remains the same, as the body is still on the same rough level surface. Therefore, the normal force can be considered constant.
- Let's assume the new frictional force is F (to be determined).
Using the formula for frictional force, we have:
F = μN (equation 2)
- We can compare equations 1 and 2 to find the relationship between the frictional force and the velocity of the body.
Since the normal force is constant, we can cancel it out from both equations:
10 N = μN
F = μN
- Now, let's compare the velocities:
2 m/s ≠ 4 m/s
- From this comparison, we can conclude that the frictional force is not directly proportional to the velocity of the body.
- Therefore, we cannot directly use the given frictional force of 10 N to find the frictional force when the velocity is 4 m/s.
- Hence, without any additional information or assumptions about the coefficient of friction, we cannot determine the exact value of the frictional force when the velocity of the body is 4 m/s.
- Therefore, the correct answer cannot be determined and none of the given options (a, b, c, d) are correct.
In figure, coefficient of friction between m2 and the horizontal surface is μ, minimum value of m so that the system has zero acceleration, is 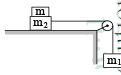
- a)μ(m1 + m2)
- b)μ(m1 – m2)
- c)m2 – (m1/μ)
- d)(m1/μ) - m2
Correct answer is option 'D'. Can you explain this answer?
In figure, coefficient of friction between m2 and the horizontal surface is μ, minimum value of m so that the system has zero acceleration, is
a)
μ(m1 + m2)
b)
μ(m1 – m2)
c)
m2 – (m1/μ)
d)
(m1/μ) - m2

|
Anjali Deshpande answered |
For zero acceleration,
Putting force = Frictional force m1g = μ(m2 + m)g
The coefficient of static friction μ between block A of mass 2kg and the table as shown in the figure is 0.2. What would be the maximum mass value of block B so that the two blocks do not move? The string and the pulley are assumed to be smooth and massless (g = 10 m/s2) 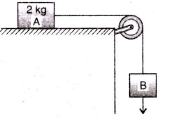
- a)2.0kg
- b)4.0 kg
- c)0.2 kg
- d)0.4 kg
Correct answer is option 'D'. Can you explain this answer?
The coefficient of static friction μ between block A of mass 2kg and the table as shown in the figure is 0.2. What would be the maximum mass value of block B so that the two blocks do not move? The string and the pulley are assumed to be smooth and massless (g = 10 m/s2)
a)
2.0kg
b)
4.0 kg
c)
0.2 kg
d)
0.4 kg

|
Anuj Choudhury answered |
For the equilibrium, mBg = μmAg
In the system shown in the adjoining figure, the acceleration of the 1 kg mass is 
- a)
g/4 downwards - b)g/4 upward
- c)g/2 downwards
- d)g/2 upward
Correct answer is option 'D'. Can you explain this answer?
In the system shown in the adjoining figure, the acceleration of the 1 kg mass is
a)
g/4 downwards
b)
g/4 upward
c)
g/2 downwards
d)
g/2 upward

|
Maheshwar Malik answered |
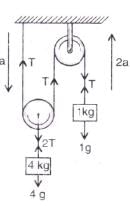
Suppose a be the downward acceleration of the 4 kg mass, therefore, 2 a is the upward acceleration of the I kg mass. Hence, equations of motion are:
Adding, after multiplying the equation (i) by 2.
Thus, the acceleration of the mass
a 1 kg is g/2 upwards.
a 1 kg is g/2 upwards.
Two wooden blocks are moving on a smooth horizontal surface such that the mass m remains stationary with respect to block of mass M as shown in figure. The magnitude of force P is 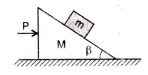
- a)(M + m)g tan β
- b)Mg tanβ
- c)(M + m)g cos β
- d)(M + m) g cosecβ
Correct answer is option 'A'. Can you explain this answer?
Two wooden blocks are moving on a smooth horizontal surface such that the mass m remains stationary with respect to block of mass M as shown in figure. The magnitude of force P is
a)
(M + m)g tan β
b)
Mg tanβ
c)
(M + m)g cos β
d)
(M + m) g cosecβ

|
Rohit Joshi answered |
The difterent torces acting on mass m are shown in the adjoining figure. Acceleration of the system
A conveyor belt is moving at a constant speed of 2 m/s. A box is gently dropped on it. The coefficient of friction between them is m = 0.5. The distance that the box will move relative to belt before coming to rest on it, taking g = 10 m/s2, is - a)0.4 m
- b)1.2 m
- c)0.6 m
- d)zero
Correct answer is option 'A'. Can you explain this answer?
A conveyor belt is moving at a constant speed of 2 m/s. A box is gently dropped on it. The coefficient of friction between them is m = 0.5. The distance that the box will move relative to belt before coming to rest on it, taking g = 10 m/s2, is
a)
0.4 m
b)
1.2 m
c)
0.6 m
d)
zero

|
Bhargavi Chopra answered |
Chapter doubts & questions for Force and Motion - Physics 2025 is part of Grade 9 exam preparation. The chapters have been prepared according to the Grade 9 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Grade 9 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Force and Motion - Physics in English & Hindi are available as part of Grade 9 exam.
Download more important topics, notes, lectures and mock test series for Grade 9 Exam by signing up for free.
Physics
307 videos|482 docs|202 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup