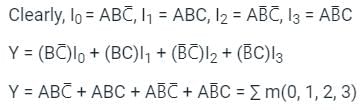All Exams >
Electrical Engineering (EE) >
6 Months Preparation for GATE Electrical >
All Questions
All questions of Combinational Logic for Electrical Engineering (EE) Exam
A logic circuit which perform the function of half-adder has:- a)3 inputs and 2 outputs
- b)2 inputs and 2 outputs
- c)1 input and 2 outputs
- d)2 inputs and 1 output
Correct answer is option 'B'. Can you explain this answer?
A logic circuit which perform the function of half-adder has:
a)
3 inputs and 2 outputs
b)
2 inputs and 2 outputs
c)
1 input and 2 outputs
d)
2 inputs and 1 output

|
Pioneer Academy answered |
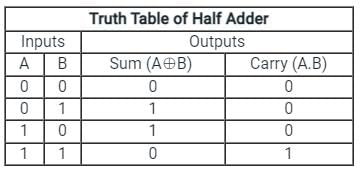
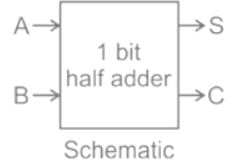
Half Adder:
- It is a Combinational Logic Circuit with two inputs and two outputs.
- It is the basic building block for the addition of two single-bit numbers.
- The half-adder circuit is designed to add two single-bit binary numbers.
- The outputs of the circuit are Sum and Carry.
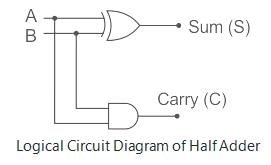
- XOR gate is used to realize Sum.
- AND gate is used to realize Carry.
The output Y of a 2-bit comparator is logic 1 whenever the 2-bit input A is greater than the 2-bit input B. The number of combinations for which the output is logic 1, is- a)4
- b)6
- c)8
- d)10
Correct answer is option 'B'. Can you explain this answer?
The output Y of a 2-bit comparator is logic 1 whenever the 2-bit input A is greater than the 2-bit input B. The number of combinations for which the output is logic 1, is
a)
4
b)
6
c)
8
d)
10

|
Cstoppers Instructors answered |
The only possible combinations are
A = 01 and B = 0 0
A = 10 and B = 00, 01
A = 11 and B = 00, 01, 10
So there are only 6 combinations
Tips and Tricks:
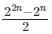
where n = 2 bit
A = 01 and B = 0 0
A = 10 and B = 00, 01
A = 11 and B = 00, 01, 10
So there are only 6 combinations
Tips and Tricks:
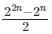
where n = 2 bit
How many OR gates are required for a Decimal-to-bcd encoder?- a)2
- b)10
- c)3
- d)4
Correct answer is option 'D'. Can you explain this answer?
How many OR gates are required for a Decimal-to-bcd encoder?
a)
2
b)
10
c)
3
d)
4
|
|
Pooja Patel answered |
An encoder is a combinational circuit encoding the information of 2n input lines to n output lines, thus producing the binary equivalent of the input.
This is clear from the diagram that it requires 4 OR gates:
This is clear from the diagram that it requires 4 OR gates:
In parts of the processor, adders are used to calculate ____________- a)Addresses
- b)Table indices
- c)Increment and decrement operators
- d)All of the Mentioned
Correct answer is option 'D'. Can you explain this answer?
In parts of the processor, adders are used to calculate ____________
a)
Addresses
b)
Table indices
c)
Increment and decrement operators
d)
All of the Mentioned
|
|
Snehal Rane answered |
Adders are used in various parts of a processor to perform arithmetic calculations. The correct answer is option 'D', which states that adders are used to calculate addresses, table indices, and increment and decrement operators. Let's explore each of these in detail:
1. Addresses:
In a processor, addresses are used to access data from memory or registers. Adders are used to perform address calculations, such as adding an offset to a base address or calculating the next memory address in a sequence. By using adders, the processor can efficiently calculate the desired address for fetching or storing data.
2. Table indices:
In many cases, processors use tables or arrays to store data. To access a specific element in a table, the processor needs to calculate the index of the desired element. Adders can be used to perform this calculation by adding the base address of the table with an offset or an index value. The result obtained from the adder is used to access the desired element in the table.
3. Increment and decrement operators:
Processors often need to increment or decrement the value of a variable or a memory location. Adders can be used to perform these operations efficiently. For example, to increment a value by one, the processor can use an adder to add the value with 1. Similarly, to decrement a value by one, the processor can use an adder to subtract 1 from the value.
By incorporating adders in different parts of the processor, these arithmetic calculations can be performed efficiently and quickly. Adders are a fundamental component of the arithmetic logic unit (ALU) in a processor. They can perform addition, subtraction, and other basic arithmetic operations, making them an essential part of the processor's functionality.
In conclusion, adders are used in various parts of a processor to calculate addresses, table indices, and perform increment and decrement operations. They play a crucial role in enabling efficient arithmetic calculations within the processor.
1. Addresses:
In a processor, addresses are used to access data from memory or registers. Adders are used to perform address calculations, such as adding an offset to a base address or calculating the next memory address in a sequence. By using adders, the processor can efficiently calculate the desired address for fetching or storing data.
2. Table indices:
In many cases, processors use tables or arrays to store data. To access a specific element in a table, the processor needs to calculate the index of the desired element. Adders can be used to perform this calculation by adding the base address of the table with an offset or an index value. The result obtained from the adder is used to access the desired element in the table.
3. Increment and decrement operators:
Processors often need to increment or decrement the value of a variable or a memory location. Adders can be used to perform these operations efficiently. For example, to increment a value by one, the processor can use an adder to add the value with 1. Similarly, to decrement a value by one, the processor can use an adder to subtract 1 from the value.
By incorporating adders in different parts of the processor, these arithmetic calculations can be performed efficiently and quickly. Adders are a fundamental component of the arithmetic logic unit (ALU) in a processor. They can perform addition, subtraction, and other basic arithmetic operations, making them an essential part of the processor's functionality.
In conclusion, adders are used in various parts of a processor to calculate addresses, table indices, and perform increment and decrement operations. They play a crucial role in enabling efficient arithmetic calculations within the processor.
A Shift register in which the output of the last flip-flop is connected to the input of the first flip-flop- a)BCD counter
- b)Parallel counter
- c)Ripple counter
- d)Ring counter
Correct answer is option 'D'. Can you explain this answer?
A Shift register in which the output of the last flip-flop is connected to the input of the first flip-flop
a)
BCD counter
b)
Parallel counter
c)
Ripple counter
d)
Ring counter
|
|
Pooja Patel answered |
The Ring shift counter is a recirculating register in which the serial output is connected back to the serial input as shown:
A Straight ring counter with ‘n’ flip-flops will have n states.
Important Points
Johnson Counter:

A Straight ring counter with ‘n’ flip-flops will have n states.
Important Points
Johnson Counter:
A Johnson counter is a modified ring counter, where the inverted output from the last flip flop is connected to the input to the first.
The MOD of the Johnson counter is 2n if n flip-flops are used.
The circuit diagram for a 4-bit Johnson Counter is as shown:
Ripple Counter:

Ripple Counter:
A ripple counter is an asynchronous counter where only the first flip-flop is clocked by an external clock.
All subsequent flip-flops are clocked by the output of the preceding flip-flop
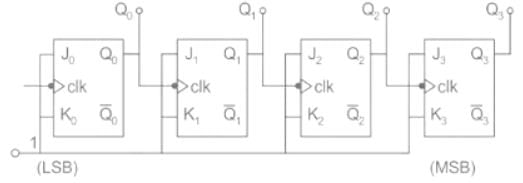
Parallel Counter:

Parallel Counter:
A parallel counter is a combinational logic circuit that receives a set of binary count signals in parallel and determines the final count after some fixed delay.

Which one of the following statements is true about the digital circuit shown in the figure?
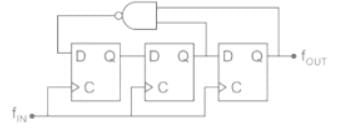
- a)It can be used for dividing the input frequency by 3.
- b)It can be used for dividing the input frequency by 5.
- c)It can be used for dividing the input frequency by 7.
- d)It cannot be reliably used as a frequency divider due to disjoint internal cycles.
Correct answer is option 'B'. Can you explain this answer?
Which one of the following statements is true about the digital circuit shown in the figure?


a)
It can be used for dividing the input frequency by 3.
b)
It can be used for dividing the input frequency by 5.
c)
It can be used for dividing the input frequency by 7.
d)
It cannot be reliably used as a frequency divider due to disjoint internal cycles.

|
Cstoppers Instructors answered |

From the given circuit diagram,

The output QA, QB, QC is repeating for every 5 clock pulses.
Hence frequency will be divided by 5.
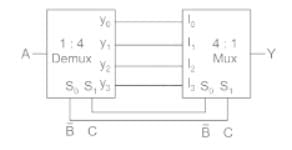
The logic function implemented by the following 4: 1 MUX is:
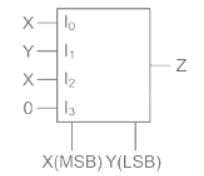
- a)Z = X and Y
- b)Z = X or Y
- c)Z = X XOR Y
- d)Z = X XNOR Y
Correct answer is option 'C'. Can you explain this answer?
The logic function implemented by the following 4: 1 MUX is:


a)
Z = X and Y
b)
Z = X or Y
c)
Z = X XOR Y
d)
Z = X XNOR Y
|
|
Pooja Patel answered |
Calculation:
For the given MUX, the output is given by,
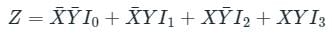
Given I0 = X, I1 = Y, I2 = X and I3 = 0
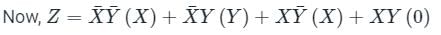
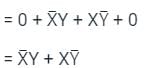
= X ⊕ Y (X-OR gate)
So, option (c)
Find the number of 2 × 1 MUX (multiplexers) required to implement 16 × 1 MUX.- a)15
- b)20
- c)5
- d)9
Correct answer is option 'A'. Can you explain this answer?
Find the number of 2 × 1 MUX (multiplexers) required to implement 16 × 1 MUX.
a)
15
b)
20
c)
5
d)
9
|
|
Mayank Sengupta answered |
It seems like you were cut off mid-sentence. Could you please provide more context or complete your question?
Minimum number of Half adders, Full adders, AND gates required to implement 2 × 3 multiplier is given as- a)1, 2, 6
- b)1, 1, 6
- c)2, 2, 6
- d)2, 1, 6
Correct answer is option 'D'. Can you explain this answer?
Minimum number of Half adders, Full adders, AND gates required to implement 2 × 3 multiplier is given as
a)
1, 2, 6
b)
1, 1, 6
c)
2, 2, 6
d)
2, 1, 6
|
|
Bijoy Nair answered |
To implement a 2-bit adder, we need to add two 2-bit numbers. This requires adding two pairs of bits, as well as carrying any overflow from the previous bit.
To add two bits, we can use a half adder. A half adder takes two inputs and produces a sum and a carry output. So, to add two pairs of bits, we need two half adders.
For the overflow bit, we need to add the carry output from the first half adder to the third input bit. This can be done with another half adder.
Therefore, we need a total of 3 half adders to implement a 2-bit adder.
In addition to the half adders, we also need AND gates to generate the carry inputs for the second and third half adders. Each half adder requires one carry input, so we need two AND gates to generate these inputs.
Therefore, the minimum number of half adders and AND gates required to implement a 2-bit adder is 3 half adders and 2 AND gates.
To add two bits, we can use a half adder. A half adder takes two inputs and produces a sum and a carry output. So, to add two pairs of bits, we need two half adders.
For the overflow bit, we need to add the carry output from the first half adder to the third input bit. This can be done with another half adder.
Therefore, we need a total of 3 half adders to implement a 2-bit adder.
In addition to the half adders, we also need AND gates to generate the carry inputs for the second and third half adders. Each half adder requires one carry input, so we need two AND gates to generate these inputs.
Therefore, the minimum number of half adders and AND gates required to implement a 2-bit adder is 3 half adders and 2 AND gates.
A 4-bit synchronous counter uses flip-flops with a propagation delay time of 15 ns each. The maximum possible time required for change of state will be - a)15 ns
- b)30 ns
- c)60 ns
- d)none of the above
Correct answer is option 'A'. Can you explain this answer?
A 4-bit synchronous counter uses flip-flops with a propagation delay time of 15 ns each. The maximum possible time required for change of state will be
a)
15 ns
b)
30 ns
c)
60 ns
d)
none of the above
|
|
Sneha Bose answered |
Introduction:
A synchronous counter is a sequential circuit that counts in a specific sequence and its outputs change simultaneously in response to an input clock signal. This type of counter is commonly used in digital electronics for various applications.
Given Information:
- 4-bit synchronous counter
- Flip-flops with a propagation delay time of 15 ns each
Explanation:
In a synchronous counter, the output of each flip-flop serves as the clock input for the next flip-flop. This ensures that all the flip-flops change state simultaneously, making the counter synchronous. The maximum possible time required for a change of state depends on the propagation delay time of the flip-flops used.
Propagation Delay Time:
Propagation delay time is the time it takes for a change in the input of a flip-flop to be reflected in its output. In this case, the given flip-flops have a propagation delay time of 15 ns each. This means that it takes 15 ns for the output of a flip-flop to change after a change in its input.
Maximum Time for Change of State:
In a 4-bit synchronous counter, all the flip-flops change state simultaneously. The maximum time required for a change of state occurs when the last flip-flop changes state after the first flip-flop. This is because the output of the first flip-flop serves as the clock input for the second flip-flop, and so on.
Since each flip-flop has a propagation delay time of 15 ns, the maximum time required for a change of state in the 4-bit synchronous counter would be equal to the propagation delay time of a single flip-flop. Therefore, the maximum possible time required for a change of state in this case is 15 ns.
Conclusion:
The maximum possible time required for a change of state in a 4-bit synchronous counter using flip-flops with a propagation delay time of 15 ns each is 15 ns.
A synchronous counter is a sequential circuit that counts in a specific sequence and its outputs change simultaneously in response to an input clock signal. This type of counter is commonly used in digital electronics for various applications.
Given Information:
- 4-bit synchronous counter
- Flip-flops with a propagation delay time of 15 ns each
Explanation:
In a synchronous counter, the output of each flip-flop serves as the clock input for the next flip-flop. This ensures that all the flip-flops change state simultaneously, making the counter synchronous. The maximum possible time required for a change of state depends on the propagation delay time of the flip-flops used.
Propagation Delay Time:
Propagation delay time is the time it takes for a change in the input of a flip-flop to be reflected in its output. In this case, the given flip-flops have a propagation delay time of 15 ns each. This means that it takes 15 ns for the output of a flip-flop to change after a change in its input.
Maximum Time for Change of State:
In a 4-bit synchronous counter, all the flip-flops change state simultaneously. The maximum time required for a change of state occurs when the last flip-flop changes state after the first flip-flop. This is because the output of the first flip-flop serves as the clock input for the second flip-flop, and so on.
Since each flip-flop has a propagation delay time of 15 ns, the maximum time required for a change of state in the 4-bit synchronous counter would be equal to the propagation delay time of a single flip-flop. Therefore, the maximum possible time required for a change of state in this case is 15 ns.
Conclusion:
The maximum possible time required for a change of state in a 4-bit synchronous counter using flip-flops with a propagation delay time of 15 ns each is 15 ns.
In full adder, there are- a)Two binary number inputs and two outputs
- b)Three binary digit inputs and two binary digit outputs
- c)Three binary digit inputs and three binary digit outputs
- d)NAND and OR gates
Correct answer is option 'B'. Can you explain this answer?
In full adder, there are
a)
Two binary number inputs and two outputs
b)
Three binary digit inputs and two binary digit outputs
c)
Three binary digit inputs and three binary digit outputs
d)
NAND and OR gates
|
|
Rajesh Kumar answered |
Full Adder:
A full adder is a combinational logic circuit that adds three binary digits and produces a sum and a carry output. It is an essential component in arithmetic circuits, such as arithmetic logic units (ALUs) and microprocessors.
Inputs and Outputs:
A full adder has three inputs - two binary numbers (A and B) to be added and a carry-in (Cin) from the previous stage. It has two outputs - a sum (S) and a carry-out (Cout). The sum output represents the least significant bit (LSB) of the addition result, while the carry-out represents the most significant bit (MSB) or the carry-over.
Binary Digit Inputs:
The question states that a full adder has three binary digit inputs. This means that each input can take on one of two values - 0 or 1. The two binary numbers (A and B) represent the bits to be added, and the carry-in (Cin) represents the carry-over from the previous stage.
Binary Digit Outputs:
The full adder has two binary digit outputs. The sum output (S) represents the bit that results from adding the two input bits and the carry-in. The carry-out (Cout) represents the bit that is carried over to the next stage of the addition.
Explanation of Option B:
Option B states that a full adder has three binary digit inputs and two binary digit outputs, which aligns with the definition and operation of a full adder. The three inputs (A, B, and Cin) are binary digits, and the two outputs (S and Cout) are also binary digits.
Other Options:
Option A states that a full adder has two binary number inputs and two outputs, which is incorrect. A full adder requires three inputs - two binary digits and a carry-in. Option C states that a full adder has three binary digit inputs and three binary digit outputs, which is also incorrect. A full adder has two outputs - a sum and a carry-out. Option D mentions NAND and OR gates, which are components used to implement the logic of a full adder, but it does not accurately describe the inputs and outputs of a full adder.
Therefore, the correct answer is option B - a full adder has three binary digit inputs and two binary digit outputs.
A full adder is a combinational logic circuit that adds three binary digits and produces a sum and a carry output. It is an essential component in arithmetic circuits, such as arithmetic logic units (ALUs) and microprocessors.
Inputs and Outputs:
A full adder has three inputs - two binary numbers (A and B) to be added and a carry-in (Cin) from the previous stage. It has two outputs - a sum (S) and a carry-out (Cout). The sum output represents the least significant bit (LSB) of the addition result, while the carry-out represents the most significant bit (MSB) or the carry-over.
Binary Digit Inputs:
The question states that a full adder has three binary digit inputs. This means that each input can take on one of two values - 0 or 1. The two binary numbers (A and B) represent the bits to be added, and the carry-in (Cin) represents the carry-over from the previous stage.
Binary Digit Outputs:
The full adder has two binary digit outputs. The sum output (S) represents the bit that results from adding the two input bits and the carry-in. The carry-out (Cout) represents the bit that is carried over to the next stage of the addition.
Explanation of Option B:
Option B states that a full adder has three binary digit inputs and two binary digit outputs, which aligns with the definition and operation of a full adder. The three inputs (A, B, and Cin) are binary digits, and the two outputs (S and Cout) are also binary digits.
Other Options:
Option A states that a full adder has two binary number inputs and two outputs, which is incorrect. A full adder requires three inputs - two binary digits and a carry-in. Option C states that a full adder has three binary digit inputs and three binary digit outputs, which is also incorrect. A full adder has two outputs - a sum and a carry-out. Option D mentions NAND and OR gates, which are components used to implement the logic of a full adder, but it does not accurately describe the inputs and outputs of a full adder.
Therefore, the correct answer is option B - a full adder has three binary digit inputs and two binary digit outputs.
How many number of 2-input NAND gates are required to realise a half adder circuit?- a)5
- b)6
- c)4
- d)8
Correct answer is option 'A'. Can you explain this answer?
How many number of 2-input NAND gates are required to realise a half adder circuit?
a)
5
b)
6
c)
4
d)
8
|
|
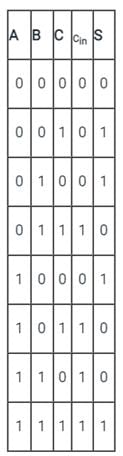
Manoj Chaudhary answered |
Understanding Half Adder
A half adder is a digital circuit that computes the sum of two binary digits. It has two main outputs:
- Sum (S): Represents the addition of A and B.
- Carry (C): Represents the carry from the addition.
The truth table for a half adder is as follows:
| A | B | Sum (S) | Carry (C) |
|---|---|---------|-----------|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Designing Half Adder Using NAND Gates
To realize a half adder using 2-input NAND gates, we need to derive the Sum and Carry expressions based on the truth table.
- Sum (S) can be expressed as: A XOR B
- Carry (C) can be expressed as: A AND B
Using NAND gates, we can derive these functions as follows:
Sum (S) Logic
1. A NAND B gives us the complement of A AND B.
2. To achieve A XOR B using NAND gates, we can manipulate the outputs of NAND gates:
- S = (A NAND (A NAND B)) NAND (B NAND (A NAND B))
Carry (C) Logic
1. To find Carry (C = A AND B):
- C = (A NAND B) NAND (A NAND B)
Counting the NAND Gates
- For Sum (S): 4 NAND gates are needed.
- For Carry (C): 1 NAND gate is needed.
Thus, the total number of 2-input NAND gates required to realize a half adder is:
- Total = 4 (for S) + 1 (for C) = 5 NAND gates.
Conclusion
Therefore, the correct answer is option 'A': 5 NAND gates are required to realize a half adder circuit.
A half adder is a digital circuit that computes the sum of two binary digits. It has two main outputs:
- Sum (S): Represents the addition of A and B.
- Carry (C): Represents the carry from the addition.
The truth table for a half adder is as follows:
| A | B | Sum (S) | Carry (C) |
|---|---|---------|-----------|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Designing Half Adder Using NAND Gates
To realize a half adder using 2-input NAND gates, we need to derive the Sum and Carry expressions based on the truth table.
- Sum (S) can be expressed as: A XOR B
- Carry (C) can be expressed as: A AND B
Using NAND gates, we can derive these functions as follows:
Sum (S) Logic
1. A NAND B gives us the complement of A AND B.
2. To achieve A XOR B using NAND gates, we can manipulate the outputs of NAND gates:
- S = (A NAND (A NAND B)) NAND (B NAND (A NAND B))
Carry (C) Logic
1. To find Carry (C = A AND B):
- C = (A NAND B) NAND (A NAND B)
Counting the NAND Gates
- For Sum (S): 4 NAND gates are needed.
- For Carry (C): 1 NAND gate is needed.
Thus, the total number of 2-input NAND gates required to realize a half adder is:
- Total = 4 (for S) + 1 (for C) = 5 NAND gates.
Conclusion
Therefore, the correct answer is option 'A': 5 NAND gates are required to realize a half adder circuit.
Consider the multiplexer based logic circuit shown in the figure.

Which one of the following Boolean functions is realized by the circuit?- a)
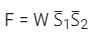
- b)F = WS1 + WS2 + S1S2
- c)
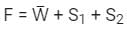
- d)F = W ⊕ S1 ⊕ S2
Correct answer is option 'D'. Can you explain this answer?
Consider the multiplexer based logic circuit shown in the figure.

Which one of the following Boolean functions is realized by the circuit?

Which one of the following Boolean functions is realized by the circuit?
a)
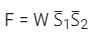
b)
F = WS1 + WS2 + S1S2
c)
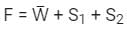
d)
F = W ⊕ S1 ⊕ S2

|
Cstoppers Instructors answered |
Concept:
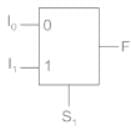
For a 2 × 1 MUX is shown above, the output function F is expressed as:
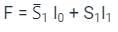
i.e. when S1 = 0, I0 is transmitted to the output.

For a 2 × 1 MUX is shown above, the output function F is expressed as:
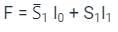
i.e. when S1 = 0, I0 is transmitted to the output.
And when S1 = 1, I1 is transmitted to the output.
Application:
The given circuit is redrawn as:
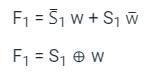
Now, the required function f will be:
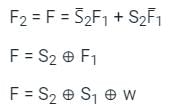
The given circuit is redrawn as:

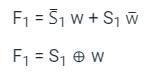
Now, the required function f will be:
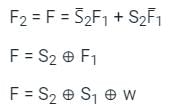
If A, B and C are the inputs of a full adder then the sum is given by __________- a)A AND B AND C
- b)A OR B AND C
- c)A XOR B XOR C
- d)A OR B OR C
Correct answer is option 'C'. Can you explain this answer?
If A, B and C are the inputs of a full adder then the sum is given by __________
a)
A AND B AND C
b)
A OR B AND C
c)
A XOR B XOR C
d)
A OR B OR C
|
|
Kalyan Patel answered |
Full Adder and its Inputs
A full adder is a combinational logic circuit that performs the addition of three bits. The three input bits of a full adder are A, B, and C (where C is the carry bit from the previous addition). The circuit adds the three bits and produces two outputs: Sum and Carry.
Sum Output of a Full Adder
The Sum output of a full adder is the result of adding the three input bits. The sum is calculated using the XOR (exclusive OR) gate. The XOR gate produces a 1 output when the inputs are different, and a 0 output when the inputs are the same. Therefore, the sum output of a full adder is given by:
Sum = A XOR B XOR C
Explanation:
- When A and B are different, the XOR gate produces a 1 output.
- If C is 1, then the XOR gate produces a 0 output because the carry bit is already included in the previous addition.
- If C is 0, then the XOR gate produces a 1 output because there is no carry bit to include in the addition.
- When A and B are the same, the XOR gate produces a 0 output.
- If C is 1, then the XOR gate produces a 1 output because the carry bit needs to be included in the addition.
- If C is 0, then the XOR gate produces a 0 output because there is no carry bit to include in the addition.
Therefore, the sum output of a full adder is given by A XOR B XOR C.
Conclusion
In conclusion, the sum output of a full adder is calculated using the XOR gate. The XOR gate produces a 1 output when the inputs are different, and a 0 output when the inputs are the same. Therefore, the sum output of a full adder is given by A XOR B XOR C.
A full adder is a combinational logic circuit that performs the addition of three bits. The three input bits of a full adder are A, B, and C (where C is the carry bit from the previous addition). The circuit adds the three bits and produces two outputs: Sum and Carry.
Sum Output of a Full Adder
The Sum output of a full adder is the result of adding the three input bits. The sum is calculated using the XOR (exclusive OR) gate. The XOR gate produces a 1 output when the inputs are different, and a 0 output when the inputs are the same. Therefore, the sum output of a full adder is given by:
Sum = A XOR B XOR C
Explanation:
- When A and B are different, the XOR gate produces a 1 output.
- If C is 1, then the XOR gate produces a 0 output because the carry bit is already included in the previous addition.
- If C is 0, then the XOR gate produces a 1 output because there is no carry bit to include in the addition.
- When A and B are the same, the XOR gate produces a 0 output.
- If C is 1, then the XOR gate produces a 1 output because the carry bit needs to be included in the addition.
- If C is 0, then the XOR gate produces a 0 output because there is no carry bit to include in the addition.
Therefore, the sum output of a full adder is given by A XOR B XOR C.
Conclusion
In conclusion, the sum output of a full adder is calculated using the XOR gate. The XOR gate produces a 1 output when the inputs are different, and a 0 output when the inputs are the same. Therefore, the sum output of a full adder is given by A XOR B XOR C.
A ________ arithmetic circuit adds two binary digits, giving a sum bit and a carry bit.- a)half-adder
- b)full-subtractor
- c)full-adder
- d)half-subtractor
Correct answer is option 'A'. Can you explain this answer?
A ________ arithmetic circuit adds two binary digits, giving a sum bit and a carry bit.
a)
half-adder
b)
full-subtractor
c)
full-adder
d)
half-subtractor
|
|
Divya Singh answered |
Half-Adder
In digital electronics, a half-adder is a basic arithmetic circuit that adds two binary digits, called the input bits, and produces two output bits: the sum bit and the carry bit. A half-adder does not take into account any carry input from previous stages.
Functionality
A half-adder has two input bits, A and B. The sum bit, denoted by S, represents the addition of the two input bits without considering any carry. The carry bit, denoted by C, represents the possible carry generated by the addition of the input bits.
The truth table for a half-adder is as follows:
A B S C
0 0 0 0
0 1 1 0
1 0 1 0
1 1 0 1
In the truth table, the S column represents the sum bit and the C column represents the carry bit. From the truth table, we can see that the sum bit (S) is obtained by performing an XOR operation on the input bits (A and B). The carry bit (C) is obtained by performing an AND operation on the input bits.
Implementation
The implementation of a half-adder can be done using two logic gates: an XOR gate and an AND gate. The XOR gate takes the input bits (A and B) and produces the sum bit (S). The AND gate takes the input bits (A and B) and produces the carry bit (C).
The circuit diagram for a half-adder is as follows:
A ----\
>--- XOR ---- S
B ----/
>--- AND ---- C
The XOR gate produces the sum bit (S) and the AND gate produces the carry bit (C).
Conclusion
A half-adder is a basic arithmetic circuit that is used to add two binary digits. It produces a sum bit and a carry bit as outputs. The sum bit represents the addition of the input bits without considering any carry, while the carry bit represents the possible carry generated by the addition. The implementation of a half-adder can be done using an XOR gate and an AND gate.
In digital electronics, a half-adder is a basic arithmetic circuit that adds two binary digits, called the input bits, and produces two output bits: the sum bit and the carry bit. A half-adder does not take into account any carry input from previous stages.
Functionality
A half-adder has two input bits, A and B. The sum bit, denoted by S, represents the addition of the two input bits without considering any carry. The carry bit, denoted by C, represents the possible carry generated by the addition of the input bits.
The truth table for a half-adder is as follows:
A B S C
0 0 0 0
0 1 1 0
1 0 1 0
1 1 0 1
In the truth table, the S column represents the sum bit and the C column represents the carry bit. From the truth table, we can see that the sum bit (S) is obtained by performing an XOR operation on the input bits (A and B). The carry bit (C) is obtained by performing an AND operation on the input bits.
Implementation
The implementation of a half-adder can be done using two logic gates: an XOR gate and an AND gate. The XOR gate takes the input bits (A and B) and produces the sum bit (S). The AND gate takes the input bits (A and B) and produces the carry bit (C).
The circuit diagram for a half-adder is as follows:
A ----\
>--- XOR ---- S
B ----/
>--- AND ---- C
The XOR gate produces the sum bit (S) and the AND gate produces the carry bit (C).
Conclusion
A half-adder is a basic arithmetic circuit that is used to add two binary digits. It produces a sum bit and a carry bit as outputs. The sum bit represents the addition of the input bits without considering any carry, while the carry bit represents the possible carry generated by the addition. The implementation of a half-adder can be done using an XOR gate and an AND gate.
Identify logic function given below -
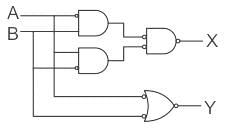
- a)Half Adder
- b)Full Adder
- c)Half Subtractor
- d)Multiplier
Correct answer is option 'A'. Can you explain this answer?
Identify logic function given below -


a)
Half Adder
b)
Full Adder
c)
Half Subtractor
d)
Multiplier

|
Cstoppers Instructors answered |
Concept:
Combinational Circuit: Combinational circuit is a circuit in which we combine the different gates in the circuit, for example, Half adder, Full Adder, Half Subtractor, Full Subtractor, encoder, decoder, multiplexer, and demultiplexer.
Combinational Circuit: Combinational circuit is a circuit in which we combine the different gates in the circuit, for example, Half adder, Full Adder, Half Subtractor, Full Subtractor, encoder, decoder, multiplexer, and demultiplexer.
→ Half Adder:
Boolean expressions for Sum and Carry (if A and B are the inputs)
Sum = A'B + AB' = ( A ⨁ B)
Carry= AB
Boolean expressions for Sum and Carry (if A and B are the inputs)
Sum = A'B + AB' = ( A ⨁ B)
Carry= AB
→ Full Adder:
Boolean expressions for Sum and Carry (if A, B and C are the inputs)
Sum = A'B'C + A'BC' + AB'C' + ABC
Carry= AB + BC + AC
Boolean expressions for Sum and Carry (if A, B and C are the inputs)
Sum = A'B'C + A'BC' + AB'C' + ABC
Carry= AB + BC + AC
→ Half Subtractor:
Boolean expressions for Difference and Borrow (if A and B are the inputs)
Difference = A'B + AB' = ( A ⨁ B)
Borrow = A'B
Boolean expressions for Difference and Borrow (if A and B are the inputs)
Difference = A'B + AB' = ( A ⨁ B)
Borrow = A'B
Analysis:
From the given circuit diagram
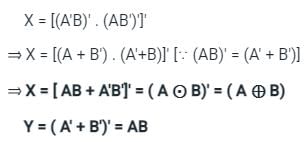
Obtained boolean expression refers to Half Adder.
From the given circuit diagram
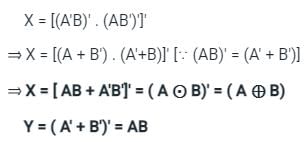
Obtained boolean expression refers to Half Adder.
A decoder converts n inputs to __________ outputs.- a)n
- b)n2
- c)2n
- d)nn
Correct answer is option 'C'. Can you explain this answer?
A decoder converts n inputs to __________ outputs.
a)
n
b)
n2
c)
2n
d)
nn
|
|
Srishti Choudhary answered |
Decoder in Digital Electronics:
Decoders are essential components in digital electronics that convert n inputs into 2^n outputs. In other words, a decoder takes a binary-coded input and activates one of its outputs based on the input combination.
Explanation:
- Number of Outputs: The number of outputs in a decoder is determined by the number of inputs it has. For n inputs, a decoder will have 2^n outputs. This is because each input line can have two possible states (0 or 1), leading to 2^n possible combinations.
- Binary to Decimal Conversion: Decoders are often used to convert binary information to decimal. For example, a 2-input decoder can be used to decode binary numbers 00, 01, 10, and 11 to corresponding decimal numbers 0, 1, 2, and 3.
- Addressing Multiple Devices: Decoders are also used in address decoding in memory and input/output devices. By using a decoder, a microprocessor can select a specific device or memory location based on the address provided.
- Applications: Decoders are widely used in various digital systems such as multiplexers, demultiplexers, memory systems, arithmetic logic units, etc. They play a crucial role in data processing and control operations.
Conclusion:
In summary, a decoder converts n inputs to 2^n outputs, making it a versatile and fundamental component in digital electronics. Understanding the working principles of decoders is essential for designing and implementing complex digital systems.
The addition of 3-bit is performed using which adder?- a)Counter
- b)Flip-flop
- c)Full adder
- d)Half adder
Correct answer is option 'C'. Can you explain this answer?
The addition of 3-bit is performed using which adder?
a)
Counter
b)
Flip-flop
c)
Full adder
d)
Half adder
|
|
Pooja Patel answered |
Half Adder: It is a logic circuit that performs addition on two binary digits. It produces a sum and carry.
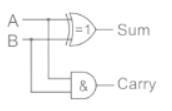
Full Adder:

Full Adder:
- It is a logic circuit that takes three inputs to perform addition.
- Two binary input and one carry-in input of the previous stage is used.
- It generates sum and carry (C-out). C-in is a carry from a less significant digit and c-out is a carry from the most significant bit.
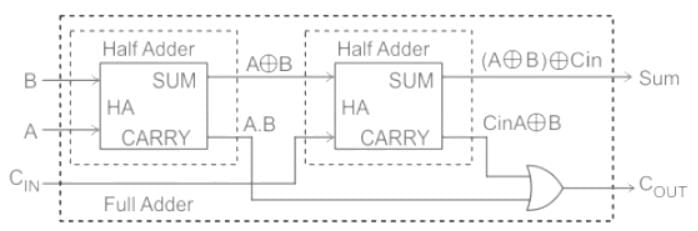
Additional Information
If we want to add two n- bit binary adders then it requires 1 half adder and n-1 full adder to complete the circuit. So, in the given question to add 4- bit binary numbers requires 1 half adder and 3 full adders.
How many OR gates are required for an octal-to-binary encoder?- a)3
- b)2
- c)8
- d)10
Correct answer is option 'A'. Can you explain this answer?
How many OR gates are required for an octal-to-binary encoder?
a)
3
b)
2
c)
8
d)
10
|
|
Ameya Nambiar answered |
**Octal-to-Binary Encoder**
An octal-to-binary encoder is a digital circuit that converts an octal input signal into a binary output signal. It takes in three inputs (A2, A1, A0) representing the octal number and produces four outputs (Y3, Y2, Y1, Y0) representing the binary number.
**Logic Diagram**
The logic diagram of an octal-to-binary encoder can be implemented using OR gates, as shown below:
```
_______
A2 --------| |
A1 --------| OR |------ Y3
A0 --------|_______|
_______
A2 --------| |
A1 --------| OR |------ Y2
A0 --------|_______|
_______
A2 --------| |
A1 --------| OR |------ Y1
A0 --------|_______|
_______
A2 --------| |
A1 --------| OR |------ Y0
A0 --------|_______|
```
**Explanation**
- The octal input signal has three bits (A2, A1, A0), representing the numbers 0 to 7.
- The binary output signal has four bits (Y3, Y2, Y1, Y0), representing the numbers 0 to 15.
- Each output bit is produced by a separate OR gate.
- The inputs A2, A1, and A0 are connected to each OR gate as shown in the logic diagram.
- The output of each OR gate will be high (1) if any of its inputs are high (1).
- Therefore, the OR gates perform a logical OR operation on the input bits and produce the corresponding output bits.
**Number of OR Gates**
To implement an octal-to-binary encoder, we need one OR gate for each output bit. Since there are four output bits (Y3, Y2, Y1, Y0), we need a total of four OR gates.
Hence, the correct answer is option A) 3.
An octal-to-binary encoder is a digital circuit that converts an octal input signal into a binary output signal. It takes in three inputs (A2, A1, A0) representing the octal number and produces four outputs (Y3, Y2, Y1, Y0) representing the binary number.
**Logic Diagram**
The logic diagram of an octal-to-binary encoder can be implemented using OR gates, as shown below:
```
_______
A2 --------| |
A1 --------| OR |------ Y3
A0 --------|_______|
_______
A2 --------| |
A1 --------| OR |------ Y2
A0 --------|_______|
_______
A2 --------| |
A1 --------| OR |------ Y1
A0 --------|_______|
_______
A2 --------| |
A1 --------| OR |------ Y0
A0 --------|_______|
```
**Explanation**
- The octal input signal has three bits (A2, A1, A0), representing the numbers 0 to 7.
- The binary output signal has four bits (Y3, Y2, Y1, Y0), representing the numbers 0 to 15.
- Each output bit is produced by a separate OR gate.
- The inputs A2, A1, and A0 are connected to each OR gate as shown in the logic diagram.
- The output of each OR gate will be high (1) if any of its inputs are high (1).
- Therefore, the OR gates perform a logical OR operation on the input bits and produce the corresponding output bits.
**Number of OR Gates**
To implement an octal-to-binary encoder, we need one OR gate for each output bit. Since there are four output bits (Y3, Y2, Y1, Y0), we need a total of four OR gates.
Hence, the correct answer is option A) 3.
If A and B are the inputs of a half adder, the carry is given by __________- a)A AND B
- b)A OR B
- c)A XOR B
- d)A EX-NOR B
Correct answer is option 'A'. Can you explain this answer?
If A and B are the inputs of a half adder, the carry is given by __________
a)
A AND B
b)
A OR B
c)
A XOR B
d)
A EX-NOR B
|
|
Pallabi Pillai answered |
Half Adder:
A half adder is a logical circuit that adds two single-bit binary numbers A and B. It has two inputs, A and B, and two outputs, the sum (S) and the carry (C).
Inputs:
In a half adder, the inputs A and B represent the two bits that need to be added.
Carry:
The carry output of a half adder is a logic gate that determines if there is a carry generated when adding A and B together. It indicates whether there is a need to carry over to the next bit when adding multiple bits.
Logic Gates:
Logic gates are the fundamental building blocks of digital circuits. They perform logical operations on one or more binary inputs to produce a single binary output.
AND Gate:
An AND gate is a logic gate that outputs a 1 if and only if all of its inputs are 1. Otherwise, it outputs a 0. The truth table for an AND gate is as follows:
```
A | B | Output
--------------
0 | 0 | 0
0 | 1 | 0
1 | 0 | 0
1 | 1 | 1
```
Explanation:
In a half adder, the carry output is determined by the AND operation between the inputs A and B. The carry output is 1 only when both inputs A and B are 1, indicating that a carry is generated.
Let's consider the inputs A and B:
```
A | B
-----
0 | 0
0 | 1
1 | 0
1 | 1
```
When A and B are both 0, the carry output is 0. When A is 0 and B is 1, or A is 1 and B is 0, the carry output is also 0. However, when A and B are both 1, the carry output is 1.
Therefore, the carry output of a half adder is given by A AND B, which corresponds to option 'A'.
A half adder is a logical circuit that adds two single-bit binary numbers A and B. It has two inputs, A and B, and two outputs, the sum (S) and the carry (C).
Inputs:
In a half adder, the inputs A and B represent the two bits that need to be added.
Carry:
The carry output of a half adder is a logic gate that determines if there is a carry generated when adding A and B together. It indicates whether there is a need to carry over to the next bit when adding multiple bits.
Logic Gates:
Logic gates are the fundamental building blocks of digital circuits. They perform logical operations on one or more binary inputs to produce a single binary output.
AND Gate:
An AND gate is a logic gate that outputs a 1 if and only if all of its inputs are 1. Otherwise, it outputs a 0. The truth table for an AND gate is as follows:
```
A | B | Output
--------------
0 | 0 | 0
0 | 1 | 0
1 | 0 | 0
1 | 1 | 1
```
Explanation:
In a half adder, the carry output is determined by the AND operation between the inputs A and B. The carry output is 1 only when both inputs A and B are 1, indicating that a carry is generated.
Let's consider the inputs A and B:
```
A | B
-----
0 | 0
0 | 1
1 | 0
1 | 1
```
When A and B are both 0, the carry output is 0. When A is 0 and B is 1, or A is 1 and B is 0, the carry output is also 0. However, when A and B are both 1, the carry output is 1.
Therefore, the carry output of a half adder is given by A AND B, which corresponds to option 'A'.
The logic shown in the given figure works as: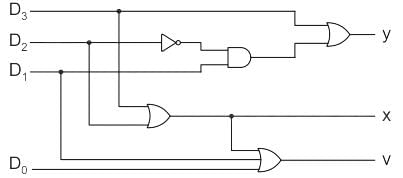
- a)decoder
- b)binary to XS-3 converter
- c)priority encoder
- d)binary to gray converter
Correct answer is option 'C'. Can you explain this answer?
The logic shown in the given figure works as:

a)
decoder
b)
binary to XS-3 converter
c)
priority encoder
d)
binary to gray converter

|
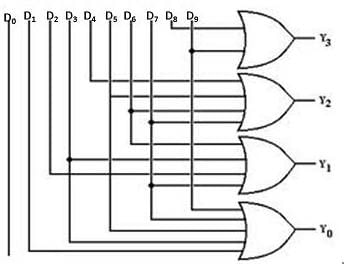
Cstoppers Instructors answered |
Priority encoder:-
If more than one input is high then encoder produce an output which may not be correct to overcome this we use priority encoder.
We considered one more output, V in order to know, whether the code available at outputs is valid or not.
If at least one input of the encoder is ‘1’, then the code available at outputs is a valid one. In this case, the output, V will be equal to 1.
If all the inputs of encoder are ‘0’, then the code available at outputs is not a valid one. In this case, the output, V will be equal to 0.
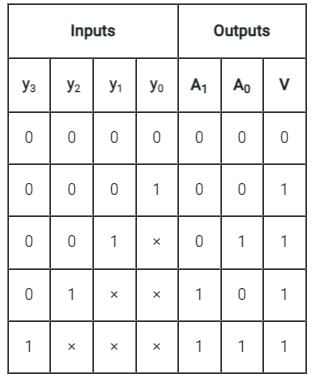
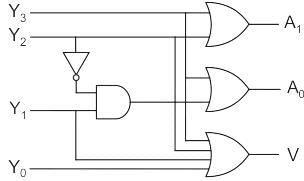
Analysis:-
Logic shown in given figure will work as
Priority encoder (4 × 2)
Inputs = D3, D2, D1, D0
Output:
y = D3 + D2’ D1
X = D3 + D2
V = D3 + D2 + D1 + D0
How many input lines are there in a ‘Full Adder’?- a)2
- b)4
- c)1
- d)3
Correct answer is option 'D'. Can you explain this answer?
How many input lines are there in a ‘Full Adder’?
a)
2
b)
4
c)
1
d)
3
|
|
Pooja Patel answered |
Combinational Logic circuits are circuits for which the present output depends only on the present input, i.e. there is no memory element to store the past output.
A combinational circuit can have ‘n’ number of inputs and ‘m’ number of outputs as shown:

Full Adder:

Full Adder:
- It is a combinational circuit used for the addition of binary numbers.
- It can add two one-bit numbers A and B, and carry C.
- The full adder is a three-input and two output combinational circuit.
The basic block diagram for a Full Adder is as shown:

A Full adder can be realized using two half adders as shown:


A Full adder can be realized using two half adders as shown:

A full adder can be implemented using 2 XOR, 2 AND, 1 OR as shown in figure:

Important Point
The truth table of a full adder logic is:


Important Point
The truth table of a full adder logic is:

The Sum output bit of a full adder is given by:
S = A ⊕ B ⊕ C
The carry output bit of a full adder is given by:
X1 = AB + BC + AC
Multiplexers:
Multiplexers:
- A multiplexer is Many to one data selector.
- A multiplexer selects one of the many data available at its input depending on the bits on the select line.
- For 2m inputs, there are m select lines that determine which input is to be connected to the output, i.e.
Number of control lines = log2(number of input lines)
Important Point
Sequential Circuits: The block diagram shown below explains this:

The memory elements used are flip flops or latches.
Important Point
Sequential Circuits: The block diagram shown below explains this:

The memory elements used are flip flops or latches.
Shift Register: A shift register has the capability to store one bit and if another bit is to store, in such situation it deletes the previous data and stores them. There are four kinds of shift registers:
- Serial-In Serial Out
- Serial-In Parallel Out
- Parallel-In serial Out
- Parallel-In Parallel Out

A ________ arithmetic circuit adds two binary digits, giving a sum bit and a carry bit.- a)half-adder
- b)full-subtractor
- c)full-adder
- d)half-subtractor
Correct answer is option 'A'. Can you explain this answer?
A ________ arithmetic circuit adds two binary digits, giving a sum bit and a carry bit.
a)
half-adder
b)
full-subtractor
c)
full-adder
d)
half-subtractor
|
|
Pooja Patel answered |
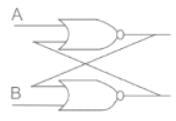
Half adder circuit have two inputs and two outputs (sum and carry).
A half adder circuit is made up of an AND gate with an XOR gate as shown below:


A half adder circuit is made up of an AND gate with an XOR gate as shown below:

- A half adder is also known as XOR gate because XOR is applied to both inputs to produce the sum
- Half adder can add only two bits (A and B) and has nothing to do with the carry
- If the input to a half adder has a carry, then it will neglect it and adds only the A and B bits
- That means the binary addition process is not complete and that's why it is called a half adder
Sum (S) = A⊕B, Carry = A.B


A 3 bit comparator circuit gives logic 1 output whenever the 3 bit input A is greater than the 3 bit input B. The output Boolean function y is represented by a K-map. The no. of 1 in the K-map is –- a)56
- b)28
- c)32
- d)24
Correct answer is option 'B'. Can you explain this answer?
A 3 bit comparator circuit gives logic 1 output whenever the 3 bit input A is greater than the 3 bit input B. The output Boolean function y is represented by a K-map. The no. of 1 in the K-map is –
a)
56
b)
28
c)
32
d)
24
|
|
Shanaya Mehta answered |
The number of 1's in the K-map depends on the values of inputs A and B. Without specific values for A and B, it is not possible to determine the number of 1's in the K-map.
The difference between half adder and full adder is __________- a)Half adder has two inputs while full adder has four inputs
- b)Half adder has one output while full adder has two outputs
- c)Half adder has two inputs while full adder has three inputs
- d)All of the Mentioned
Correct answer is option 'C'. Can you explain this answer?
The difference between half adder and full adder is __________
a)
Half adder has two inputs while full adder has four inputs
b)
Half adder has one output while full adder has two outputs
c)
Half adder has two inputs while full adder has three inputs
d)
All of the Mentioned
|
|
Pooja Patel answered |
Half adder has two inputs while full adder has three outputs; this is the difference between them, while both have two outputs SUM and CARRY.
If A and B are the inputs of a half adder, the sum is given by __________- a)A AND B
- b)A OR B
- c)A XOR B
- d)A EX-NOR B
Correct answer is option 'C'. Can you explain this answer?
If A and B are the inputs of a half adder, the sum is given by __________
a)
A AND B
b)
A OR B
c)
A XOR B
d)
A EX-NOR B
|
|
Dishani Bose answered |
Half Adder and its Inputs
A half adder is a digital circuit that is used to add two binary digits together. It has two inputs, A and B, and two outputs, sum and carry. The sum output gives the result of adding the two inputs, while the carry output indicates if there is a carry from the least significant bit to the most significant bit.
Logic Gates in Half Adder
The half adder uses two logic gates, an XOR gate and an AND gate, to perform the addition. The XOR gate gives a 1 output when one and only one of its inputs is 1. The AND gate gives a 1 output only when both of its inputs are 1.
Sum of Half Adder
To find the sum of the two binary digits using a half adder, we use the XOR gate. The sum output is the result of the XOR gate.
Sum Output
The sum output is given by the Boolean expression A XOR B. This means that if A and B are different, the sum output will be 1. If A and B are the same, the sum output will be 0.
Conclusion
Therefore, the sum output of a half adder is given by A XOR B. This is because we want the sum output to be 1 only when one of the inputs is 1, but not both. The XOR gate is the logic gate that satisfies this condition.
A half adder is a digital circuit that is used to add two binary digits together. It has two inputs, A and B, and two outputs, sum and carry. The sum output gives the result of adding the two inputs, while the carry output indicates if there is a carry from the least significant bit to the most significant bit.
Logic Gates in Half Adder
The half adder uses two logic gates, an XOR gate and an AND gate, to perform the addition. The XOR gate gives a 1 output when one and only one of its inputs is 1. The AND gate gives a 1 output only when both of its inputs are 1.
Sum of Half Adder
To find the sum of the two binary digits using a half adder, we use the XOR gate. The sum output is the result of the XOR gate.
Sum Output
The sum output is given by the Boolean expression A XOR B. This means that if A and B are different, the sum output will be 1. If A and B are the same, the sum output will be 0.
Conclusion
Therefore, the sum output of a half adder is given by A XOR B. This is because we want the sum output to be 1 only when one of the inputs is 1, but not both. The XOR gate is the logic gate that satisfies this condition.
A _________ is a multiple-input, multiple-output logic circuit which converts coded inputs into coded outputs, where the input and output code are different.- a)decoder
- b)demultiplexer
- c)multiplexer
- d)encoder
Correct answer is option 'A'. Can you explain this answer?
A _________ is a multiple-input, multiple-output logic circuit which converts coded inputs into coded outputs, where the input and output code are different.
a)
decoder
b)
demultiplexer
c)
multiplexer
d)
encoder
|
|
Arindam Sengupta answered |
A decoder is a multiple-input, multiple-output logic circuit which converts coded inputs into coded outputs, where the input and output code are different.
What is a decoder?
A decoder is a combinational logic circuit that takes coded inputs and converts them into coded outputs. It has multiple input lines and multiple output lines. The input code is different from the output code, which means that the binary information represented by the input code is decoded to produce the output code.
Working principle of a decoder
The working principle of a decoder is based on the fact that each input combination corresponds to a unique output combination. The decoder has 2^n input lines and 2^m output lines, where n is the number of input lines and m is the number of output lines. The input lines are coded in binary format, and the output lines are also coded in binary format but with a different code.
Types of decoders
1. Binary decoder: This type of decoder has n input lines and 2^n output lines. Each input combination corresponds to a unique output line. The output lines are activated based on the input code, and the remaining output lines remain inactive.
2. BCD decoder: This type of decoder is used to decode a Binary Coded Decimal (BCD) input into its corresponding decimal output. It has 4 input lines and 10 output lines, representing the decimal digits 0 to 9.
3. 7-segment decoder: This type of decoder is used to decode a binary input into a 7-segment display output. It has 4 input lines and 7 output lines, representing the segments of a 7-segment display.
Applications of decoders
Decoders are widely used in various digital systems and circuits. Some common applications include:
- Address decoding in memory systems
- Data demultiplexing
- Digital display systems
- Error detection and correction
- Control circuits in microprocessors and microcontrollers
Decoders play a crucial role in digital electronics as they enable the conversion of coded information into meaningful output. They are essential components in various digital systems and circuits, providing the necessary decoding capabilities for efficient data processing and control.
What is a decoder?
A decoder is a combinational logic circuit that takes coded inputs and converts them into coded outputs. It has multiple input lines and multiple output lines. The input code is different from the output code, which means that the binary information represented by the input code is decoded to produce the output code.
Working principle of a decoder
The working principle of a decoder is based on the fact that each input combination corresponds to a unique output combination. The decoder has 2^n input lines and 2^m output lines, where n is the number of input lines and m is the number of output lines. The input lines are coded in binary format, and the output lines are also coded in binary format but with a different code.
Types of decoders
1. Binary decoder: This type of decoder has n input lines and 2^n output lines. Each input combination corresponds to a unique output line. The output lines are activated based on the input code, and the remaining output lines remain inactive.
2. BCD decoder: This type of decoder is used to decode a Binary Coded Decimal (BCD) input into its corresponding decimal output. It has 4 input lines and 10 output lines, representing the decimal digits 0 to 9.
3. 7-segment decoder: This type of decoder is used to decode a binary input into a 7-segment display output. It has 4 input lines and 7 output lines, representing the segments of a 7-segment display.
Applications of decoders
Decoders are widely used in various digital systems and circuits. Some common applications include:
- Address decoding in memory systems
- Data demultiplexing
- Digital display systems
- Error detection and correction
- Control circuits in microprocessors and microcontrollers
Decoders play a crucial role in digital electronics as they enable the conversion of coded information into meaningful output. They are essential components in various digital systems and circuits, providing the necessary decoding capabilities for efficient data processing and control.
In order to design 5 bit comparator, how many output(s) is/are needed?- a)1
- b)2
- c)3
- d)4
Correct answer is option 'C'. Can you explain this answer?
In order to design 5 bit comparator, how many output(s) is/are needed?
a)
1
b)
2
c)
3
d)
4
|
|
Debanshi Basak answered |
Number of Outputs Needed for a 5-bit Comparator
In a 5-bit comparator, the goal is to compare two 5-bit binary numbers and determine their relationship (equal, greater than, or less than). To achieve this, multiple outputs are required to represent the comparison result.
Explanation:
1. Output for Equality:
- One output is needed to indicate whether the two 5-bit numbers are equal or not. This output will be high (1) if the numbers are equal and low (0) if they are not equal.
2. Outputs for Inequality:
- Two additional outputs are required to determine whether one 5-bit number is greater than or less than the other. These outputs will be high (1) based on the relationship between the two numbers.
Therefore, a total of 3 outputs are needed in a 5-bit comparator to provide information about the equality and inequality of the input numbers. Each output serves a specific purpose in conveying the comparison result accurately.
In a 5-bit comparator, the goal is to compare two 5-bit binary numbers and determine their relationship (equal, greater than, or less than). To achieve this, multiple outputs are required to represent the comparison result.
Explanation:
1. Output for Equality:
- One output is needed to indicate whether the two 5-bit numbers are equal or not. This output will be high (1) if the numbers are equal and low (0) if they are not equal.
2. Outputs for Inequality:
- Two additional outputs are required to determine whether one 5-bit number is greater than or less than the other. These outputs will be high (1) based on the relationship between the two numbers.
Therefore, a total of 3 outputs are needed in a 5-bit comparator to provide information about the equality and inequality of the input numbers. Each output serves a specific purpose in conveying the comparison result accurately.
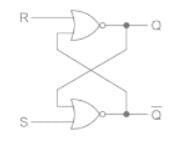
Identify the following sequential component.
- a)Master-slave flip flop
- b)Clocked flip flop
- c)J-K flip flop
- d)R-S flip flop
Correct answer is option 'D'. Can you explain this answer?
Identify the following sequential component.


a)
Master-slave flip flop
b)
Clocked flip flop
c)
J-K flip flop
d)
R-S flip flop
|
|
Pooja Patel answered |
Explanation:
The given sequential component is of RS Flip Flop.
Here A = R and B = S
The truth table for the circuit is shown:
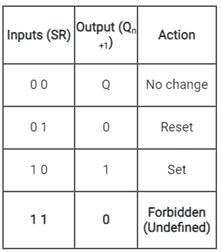
Important Points
The difference between latches and flip flops is shown
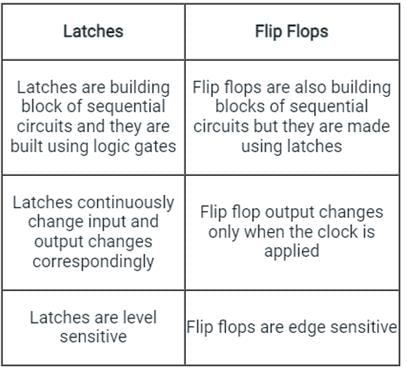

The truth table for the circuit is shown:

Important Points
The difference between latches and flip flops is shown

A __________ counter can be implemented using three flipflops.- a)mod-6
- b)mod-11
- c)mod-9
- d)mod-13
Correct answer is option 'A'. Can you explain this answer?
A __________ counter can be implemented using three flipflops.
a)
mod-6
b)
mod-11
c)
mod-9
d)
mod-13
|
|
Kritika Gupta answered |
Explanation:
In digital electronics, a counter is a sequential circuit that counts the number of occurrences of an event. A counter can be implemented using flip-flops, which are basic building blocks of sequential circuits.
Modulus Counter:
A modulus counter is a type of counter that counts up to a specific modulus value before resetting back to zero. In this case, we are looking for a counter that can count up to six before resetting.
Implementing a Mod-6 Counter:
To implement a mod-6 counter using flip-flops, we need to use three flip-flops. Each flip-flop will represent a binary digit, and the combination of these flip-flops will represent the count.
Binary Representation:
The modulus value can be represented in binary as 110, which means we need three bits to represent the count from 0 to 5.
Using D Flip-Flops:
D flip-flops are commonly used to implement counters. Each D flip-flop has two inputs - D (data) and CLK (clock). The output of one flip-flop is connected to the CLK input of the next flip-flop, creating a ripple effect.
Implementing a Mod-6 Counter using D Flip-Flops:
Here is how we can implement a mod-6 counter using three D flip-flops:
- Connect the Q output of the first flip-flop to the D input of the second flip-flop.
- Connect the Q output of the second flip-flop to the D input of the third flip-flop.
- Connect the Q output of the third flip-flop to the D input of the first flip-flop.
Working:
The counter starts at 000. On the rising edge of the clock signal, the first flip-flop increments its count by 1. When the count reaches 2 (010 in binary), the second flip-flop increments its count by 1. When the count reaches 4 (100 in binary), the third flip-flop increments its count by 1.
Reset:
When the count reaches 6 (110 in binary), the counter resets back to 000 and starts counting again. This creates a mod-6 counter.
Conclusion:
Therefore, a mod-6 counter can be implemented using three flip-flops.
In digital electronics, a counter is a sequential circuit that counts the number of occurrences of an event. A counter can be implemented using flip-flops, which are basic building blocks of sequential circuits.
Modulus Counter:
A modulus counter is a type of counter that counts up to a specific modulus value before resetting back to zero. In this case, we are looking for a counter that can count up to six before resetting.
Implementing a Mod-6 Counter:
To implement a mod-6 counter using flip-flops, we need to use three flip-flops. Each flip-flop will represent a binary digit, and the combination of these flip-flops will represent the count.
Binary Representation:
The modulus value can be represented in binary as 110, which means we need three bits to represent the count from 0 to 5.
Using D Flip-Flops:
D flip-flops are commonly used to implement counters. Each D flip-flop has two inputs - D (data) and CLK (clock). The output of one flip-flop is connected to the CLK input of the next flip-flop, creating a ripple effect.
Implementing a Mod-6 Counter using D Flip-Flops:
Here is how we can implement a mod-6 counter using three D flip-flops:
- Connect the Q output of the first flip-flop to the D input of the second flip-flop.
- Connect the Q output of the second flip-flop to the D input of the third flip-flop.
- Connect the Q output of the third flip-flop to the D input of the first flip-flop.
Working:
The counter starts at 000. On the rising edge of the clock signal, the first flip-flop increments its count by 1. When the count reaches 2 (010 in binary), the second flip-flop increments its count by 1. When the count reaches 4 (100 in binary), the third flip-flop increments its count by 1.
Reset:
When the count reaches 6 (110 in binary), the counter resets back to 000 and starts counting again. This creates a mod-6 counter.
Conclusion:
Therefore, a mod-6 counter can be implemented using three flip-flops.
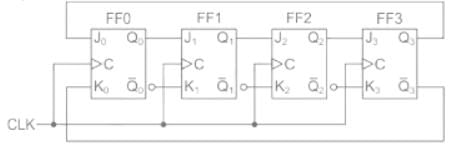
A mod–n counter using a synchronous binary up–counter with synchronous clear input is shown in the figure. The value of n is_________. (Important - Enter only the numerical value in the answer) Correct answer is '7'. Can you explain this answer?
Correct answer is '7'. Can you explain this answer?
A mod–n counter using a synchronous binary up–counter with synchronous clear input is shown in the figure. The value of n is_________.
(Important - Enter only the numerical value in the answer)


|
Cstoppers Instructors answered |
Concept:
CLR: It is an active low signal. It is activated when CLR = 0 and it resets the FF.
CLR: It is an active high signal. It is activated when CLR = 1 and it Resets the FF.
Synchronous: Synchronous clear is synchronized with the clock. It waits for a clock pulse to Reset FF output.

Synchronous: Synchronous clear is synchronized with the clock. It waits for a clock pulse to Reset FF output.
Asynchronous: Asynchronous Clear is not synchronized with the clock. It does not wait for a clock pulse to Reset FF output.
Application:
From given sequential circuit:
CLR = QB ⋅ QC
When both QB & QC equal to 1 then CLR = 0. Otherwise CLR = 1
Now,
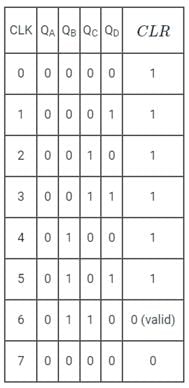
Since it is given that the counter have synchronous clear input, the output of the counter will reset at the 7th clock pulse.

Since it is given that the counter have synchronous clear input, the output of the counter will reset at the 7th clock pulse.
∴ The mod of the counter, n = 7
A full adder combinational circuit has- a)3 inputs and 2 outputs
- b)2 inputs and 0 outputs
- c)1 input and 0 output
- d)4 inputs and 1 output
Correct answer is option 'A'. Can you explain this answer?
A full adder combinational circuit has
a)
3 inputs and 2 outputs
b)
2 inputs and 0 outputs
c)
1 input and 0 output
d)
4 inputs and 1 output
|
|
Pooja Patel answered |
The basic block diagram for a Full Adder is as shown:
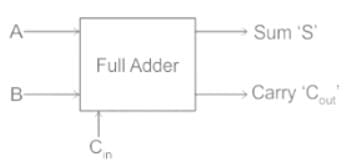
A Full adder can be realized using two half adders as shown:
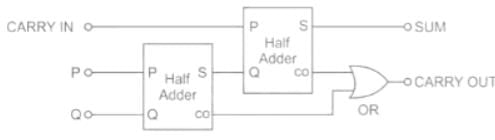

A Full adder can be realized using two half adders as shown:

We, therefore, conclude that a full adder combinational circuit has 3 inputs and 2 outputs.
A full adder can be implemented using 2 XOR, 2 AND, 1 OR as shown in figure:

Important Point
The truth table of a full adder logic is:
S = A ⊕ B ⊕ C
The Sum output bit of a full adder is given by:

Important Point
The truth table of a full adder logic is:

S = A ⊕ B ⊕ C
The Sum output bit of a full adder is given by:
The carry output bit of a full adder is given by:
X1 = AB + BC + AC
Circuit for comparing 2 n-bit numbers has ____ entries in truth table- a)2n
- b)n
- c)22n
- d)2n
Correct answer is option 'C'. Can you explain this answer?
Circuit for comparing 2 n-bit numbers has ____ entries in truth table
a)
2n
b)
n
c)
22n
d)
2n
|
|
Pooja Patel answered |
In an n-bit, compare the n columns of bits in one binary number (let it be A) and n columns of bits of another number (let it be B).
For all possible values of bits in A and B truth table is taken for A > B, A < B and A = B.
So there are 2n inputs in the comparator.
For 2n inputs total possible combinations are 22n
So total number of entries is 22n.
For all possible values of bits in A and B truth table is taken for A > B, A < B and A = B.
So there are 2n inputs in the comparator.
For 2n inputs total possible combinations are 22n
So total number of entries is 22n.
For the following cascaded Counters find the value of X of the mode-X counter. (Important - Enter only the numerical value in the answer)
Correct answer is '10'. Can you explain this answer?
For the following cascaded Counters find the value of X of the mode-X counter.
(Important - Enter only the numerical value in the answer)


|
Pioneer Academy answered |
Concept:
- The N-bit ring counter will have total N states/Mods.
- The N-bit johnson counter will have a total 2N number of states/Mods.
- The output frequency of a counter is the input frequency divided by the mode number of that counter.
Solution:

The frequency at node Y is

The frequency at node Y is
Fy = 150kHz/5
= 30 kHz
The frequency at node Z is
Fz = 30kHz/X
here X is the Mod number
then output frequency is given by
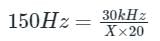
∴ X = 10
In which operation carry is obtained?- a)Subtraction
- b)Addition
- c)Multiplication
- d)Both addition and subtraction
Correct answer is option 'B'. Can you explain this answer?
In which operation carry is obtained?
a)
Subtraction
b)
Addition
c)
Multiplication
d)
Both addition and subtraction
|
|
Pooja Patel answered |
In addition, carry is obtained. For example: 1 0 1 + 1 1 1 = 1 0 0; in this example carry is obtained after 1st addition (i.e. 1 + 1 = 1 0). In subtraction, borrow is obtained. Like, 0 – 1 = 1 (borrow 1).
In half adder, the total number of inputs and outputs are:- a)1, 2
- b)2, 1
- c)3, 2
- d)2, 2
Correct answer is option 'D'. Can you explain this answer?
In half adder, the total number of inputs and outputs are:
a)
1, 2
b)
2, 1
c)
3, 2
d)
2, 2
|
|
Rajesh Verma answered |
Half Adder: Inputs and Outputs
A half adder is a digital circuit that performs addition of two binary digits. It has two inputs, which represent the two binary digits to be added, and two outputs, which represent the sum and the carry generated during the addition process.
Inputs of a Half Adder:
A half adder has two inputs:
1. Input A: This input represents the first binary digit to be added.
2. Input B: This input represents the second binary digit to be added.
Outputs of a Half Adder:
A half adder has two outputs:
1. Sum (S): This output represents the sum of the two binary digits. It takes the value of 1 if the two inputs are different and 0 if they are the same.
2. Carry (C): This output represents the carry generated during the addition process. It takes the value of 1 if both inputs are 1, indicating that a carry is generated, and 0 otherwise.
Explanation of the Correct Answer:
The correct answer is option 'D', which states that a half adder has 2 inputs and 2 outputs. This is because a half adder requires two binary digits as inputs to perform the addition operation and produces two outputs: the sum and the carry.
Visual Representation:
To visually represent the inputs and outputs of a half adder:
Inputs:
- Input A
- Input B
Outputs:
- Sum (S)
- Carry (C)
Therefore, the total number of inputs and outputs in a half adder is 2, making option 'D' the correct answer.
A half adder is a digital circuit that performs addition of two binary digits. It has two inputs, which represent the two binary digits to be added, and two outputs, which represent the sum and the carry generated during the addition process.
Inputs of a Half Adder:
A half adder has two inputs:
1. Input A: This input represents the first binary digit to be added.
2. Input B: This input represents the second binary digit to be added.
Outputs of a Half Adder:
A half adder has two outputs:
1. Sum (S): This output represents the sum of the two binary digits. It takes the value of 1 if the two inputs are different and 0 if they are the same.
2. Carry (C): This output represents the carry generated during the addition process. It takes the value of 1 if both inputs are 1, indicating that a carry is generated, and 0 otherwise.
Explanation of the Correct Answer:
The correct answer is option 'D', which states that a half adder has 2 inputs and 2 outputs. This is because a half adder requires two binary digits as inputs to perform the addition operation and produces two outputs: the sum and the carry.
Visual Representation:
To visually represent the inputs and outputs of a half adder:
Inputs:
- Input A
- Input B
Outputs:
- Sum (S)
- Carry (C)
Therefore, the total number of inputs and outputs in a half adder is 2, making option 'D' the correct answer.
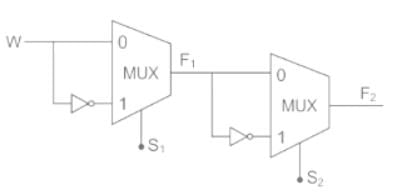
The Boolean function ‘f’ implemented as shown in the figure using two input multiplexers is:
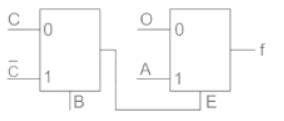
- a)

- b)
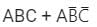
- c)
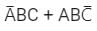
- d)
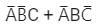
Correct answer is option 'A'. Can you explain this answer?
The Boolean function ‘f’ implemented as shown in the figure using two input multiplexers is:


a)

b)
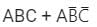
c)
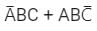
d)
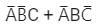
|
|
Luminary Institute answered |
Concept:

For a 2 × 1 MUX is shown above, the output function F is expressed as:
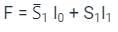
i.e. when S1 = 0, I0 is transmitted to the output.

For a 2 × 1 MUX is shown above, the output function F is expressed as:
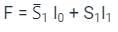
i.e. when S1 = 0, I0 is transmitted to the output.
And when S1 = 1, I1 is transmitted to the output.
Application:
The output of the 1st MUX will be:
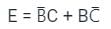
The final output will be:
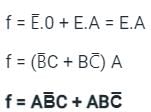
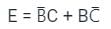
The final output will be:
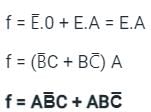
An eight-bit binary ripple UP counter with a modulus of 256 is holding the count 01111111. What will be the count after 135 clock pulses?- a)0000 0101
- b)1111 1001
- c)0000 0110
- d)0000 0111
Correct answer is option 'C'. Can you explain this answer?
An eight-bit binary ripple UP counter with a modulus of 256 is holding the count 01111111. What will be the count after 135 clock pulses?
a)
0000 0101
b)
1111 1001
c)
0000 0110
d)
0000 0111
|
|
Pooja Patel answered |
01111111 → 127
After 135 clock cycles, we will get
127 + 135 = 262
∴ The total number of clock pulses will be 262
As the modulus is 256,
After 256 clock pulses, the sequence will repeat.
262 = 256 + 6
∴ 00 00 00 00
257 → 00 00 00 01
258 → 00 00 00 10
259 → 00 00 00 11
260 → 00 00 01 00
261 → 00 00 01 01
262 → 00 00 01 10
If the input to a T flip-flop is a 100 MHz signal, the final output of three T flip-flops in a cascade is- a)1000 MHz
- b)520 MHz
- c)333 MHz
- d)12.5 MHz
Correct answer is option 'D'. Can you explain this answer?
If the input to a T flip-flop is a 100 MHz signal, the final output of three T flip-flops in a cascade is
a)
1000 MHz
b)
520 MHz
c)
333 MHz
d)
12.5 MHz
|
|
Pooja Patel answered |
Concept:
If we pass the input signal to a single T-flip flop, we will get half of the frequency at the output.

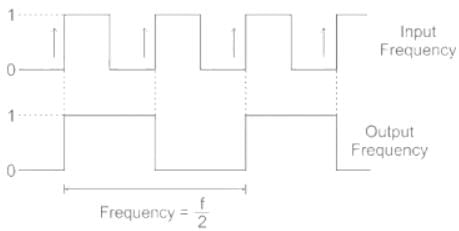
Similarly, when we pass the input signal into an n-bit flip flop counter, the output frequency (fout) will be:
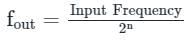
Application:


Similarly, when we pass the input signal into an n-bit flip flop counter, the output frequency (fout) will be:
Application:
Given Input frequency f = 100 Hz

fout = 12.5 Hz

fout = 12.5 Hz
How many AND, OR and EXOR gates are required for the configuration of full adder?- a)1, 2, 2
- b)2, 1, 2
- c)3, 1, 2
- d)4, 0, 1
Correct answer is option 'B'. Can you explain this answer?
How many AND, OR and EXOR gates are required for the configuration of full adder?
a)
1, 2, 2
b)
2, 1, 2
c)
3, 1, 2
d)
4, 0, 1
|
|
Ankita Das answered |
Full Adder Configuration
To understand the number of gates required for the configuration of a full adder, let's first discuss what a full adder is and its logical representation.
A full adder is a combinational circuit that takes in three inputs: A, B, and Cin (carry-in) and produces two outputs: Sum (S) and Cout (carry-out). It is used to add two binary numbers along with a carry input from the previous stage.
The logical representation of a full adder can be expressed using basic logic gates such as AND, OR, and EXOR gates.
Logical Representation of Full Adder
The logical representation of a full adder is as follows:
1. Sum (S) output:
- It is the output of the EXOR gate.
- It is calculated by taking the EXOR of A, B, and Cin.
2. Carry-out (Cout) output:
- It is the output of the OR gate.
- It is calculated by taking the OR of the AND gates' outputs.
Calculating the Number of Gates
Now, let's calculate the number of AND, OR, and EXOR gates required for the configuration of a full adder.
1. AND gates:
- We require 2 AND gates to calculate the carry-out (Cout) output.
- Each AND gate takes 2 inputs, so a total of 2 AND gates are needed.
2. OR gates:
- We require 1 OR gate to calculate the carry-out (Cout) output.
- The OR gate takes 2 inputs.
3. EXOR gates:
- We require 2 EXOR gates to calculate the sum (S) output.
- Each EXOR gate takes 3 inputs, so a total of 2 EXOR gates are needed.
Hence, the number of AND, OR, and EXOR gates required for the configuration of a full adder is as follows:
- AND gates: 2
- OR gates: 1
- EXOR gates: 2
Therefore, the correct answer is option 'B' (2, 1, 2).
To understand the number of gates required for the configuration of a full adder, let's first discuss what a full adder is and its logical representation.
A full adder is a combinational circuit that takes in three inputs: A, B, and Cin (carry-in) and produces two outputs: Sum (S) and Cout (carry-out). It is used to add two binary numbers along with a carry input from the previous stage.
The logical representation of a full adder can be expressed using basic logic gates such as AND, OR, and EXOR gates.
Logical Representation of Full Adder
The logical representation of a full adder is as follows:
1. Sum (S) output:
- It is the output of the EXOR gate.
- It is calculated by taking the EXOR of A, B, and Cin.
2. Carry-out (Cout) output:
- It is the output of the OR gate.
- It is calculated by taking the OR of the AND gates' outputs.
Calculating the Number of Gates
Now, let's calculate the number of AND, OR, and EXOR gates required for the configuration of a full adder.
1. AND gates:
- We require 2 AND gates to calculate the carry-out (Cout) output.
- Each AND gate takes 2 inputs, so a total of 2 AND gates are needed.
2. OR gates:
- We require 1 OR gate to calculate the carry-out (Cout) output.
- The OR gate takes 2 inputs.
3. EXOR gates:
- We require 2 EXOR gates to calculate the sum (S) output.
- Each EXOR gate takes 3 inputs, so a total of 2 EXOR gates are needed.
Hence, the number of AND, OR, and EXOR gates required for the configuration of a full adder is as follows:
- AND gates: 2
- OR gates: 1
- EXOR gates: 2
Therefore, the correct answer is option 'B' (2, 1, 2).
Which of the following can be represented for decoder?- a)Sequential circuit
- b)Combinational circuit
- c)Logical circuit
- d)None of the mentioned
Correct answer is option 'B'. Can you explain this answer?
Which of the following can be represented for decoder?
a)
Sequential circuit
b)
Combinational circuit
c)
Logical circuit
d)
None of the mentioned
|
|
Yashvi Shah answered |
Decoder:
A decoder is a digital circuit that converts coded input signals into a specific set of output signals. It is used in various applications such as data decoding, address decoding, and memory decoding. The main function of a decoder is to select one of the many outputs based on the input code.
Combinational Circuit:
A combinational circuit is a digital circuit that produces an output based on the current input values. It does not have any memory elements, and the output is solely determined by the current input values. Combinational circuits are designed using logic gates such as AND, OR, NOT, etc.
Sequential Circuit:
A sequential circuit is a digital circuit that has memory elements such as flip-flops. The output of a sequential circuit depends not only on the current input values but also on the previous input values and the state of the memory elements. Sequential circuits have a clock signal that controls the timing of their operation.
Logical Circuit:
A logical circuit refers to any circuit that performs logical operations such as AND, OR, NOT, etc. Both combinational and sequential circuits can be considered as logical circuits since they involve logical operations.
Representation for Decoder:
A decoder is a combinational circuit. It takes an n-bit input and produces 2^n outputs. Each output corresponds to a unique input combination. The number of outputs is determined by the number of input lines. For example, a 2-to-4 decoder has 2 input lines and produces 4 output lines.
A decoder can be represented using logic gates such as AND gates and NOT gates. The input lines are connected to the inputs of the AND gates, and their outputs are connected to the output lines. The output lines are activated based on the specific input combination. For example, if the input code is '00', the first output line is activated. If the input code is '01', the second output line is activated, and so on.
Since a decoder does not have any memory elements and its output is solely determined by the input code, it is considered as a combinational circuit. It does not depend on any previous input values or memory states. Therefore, the correct answer is option 'B' - Combinational circuit.
A decoder is a digital circuit that converts coded input signals into a specific set of output signals. It is used in various applications such as data decoding, address decoding, and memory decoding. The main function of a decoder is to select one of the many outputs based on the input code.
Combinational Circuit:
A combinational circuit is a digital circuit that produces an output based on the current input values. It does not have any memory elements, and the output is solely determined by the current input values. Combinational circuits are designed using logic gates such as AND, OR, NOT, etc.
Sequential Circuit:
A sequential circuit is a digital circuit that has memory elements such as flip-flops. The output of a sequential circuit depends not only on the current input values but also on the previous input values and the state of the memory elements. Sequential circuits have a clock signal that controls the timing of their operation.
Logical Circuit:
A logical circuit refers to any circuit that performs logical operations such as AND, OR, NOT, etc. Both combinational and sequential circuits can be considered as logical circuits since they involve logical operations.
Representation for Decoder:
A decoder is a combinational circuit. It takes an n-bit input and produces 2^n outputs. Each output corresponds to a unique input combination. The number of outputs is determined by the number of input lines. For example, a 2-to-4 decoder has 2 input lines and produces 4 output lines.
A decoder can be represented using logic gates such as AND gates and NOT gates. The input lines are connected to the inputs of the AND gates, and their outputs are connected to the output lines. The output lines are activated based on the specific input combination. For example, if the input code is '00', the first output line is activated. If the input code is '01', the second output line is activated, and so on.
Since a decoder does not have any memory elements and its output is solely determined by the input code, it is considered as a combinational circuit. It does not depend on any previous input values or memory states. Therefore, the correct answer is option 'B' - Combinational circuit.
Consider the output A and B with I0, I1, I2 and I3 as input and ‘A’ and ‘B’ as output,A = I2 + I3B = I̅2 I1 + I3The above circuit is:- a)4:1 multiplexer
- b)De-multiplexer
- c)BCD circuit
- d)Priority Encoder
Correct answer is option 'D'. Can you explain this answer?
Consider the output A and B with I0, I1, I2 and I3 as input and ‘A’ and ‘B’ as output,
A = I2 + I3
B = I̅2 I1 + I3
The above circuit is:
a)
4:1 multiplexer
b)
De-multiplexer
c)
BCD circuit
d)
Priority Encoder
|
|
Arindam Sengupta answered |
Priority Encoder:
Priority encoder is a digital circuit that converts multiple input signals into a binary-coded output based on the highest-priority input signal. It is used in digital systems to prioritize multiple inputs and encode them into a binary output.
Explanation of the given circuit:
In the given circuit, the output A is the OR combination of input signals I2 and I3, which means A = I2 + I3. The output B is the AND combination of input signals I2 and I1, along with I3, which means B = I2*I1 + I3.
Identifying the circuit type:
Based on the given inputs and outputs, it is clear that the circuit is performing encoding based on priority. The output A is dependent on I2 and I3, while the output B is dependent on I2 having higher priority over I1 and I3.
Conclusion:
Therefore, the given circuit corresponds to a Priority Encoder, which encodes multiple input signals into a binary output based on priority. This type of circuit is commonly used in digital systems to handle multiple inputs efficiently and prioritize them based on certain criteria.
Priority encoder is a digital circuit that converts multiple input signals into a binary-coded output based on the highest-priority input signal. It is used in digital systems to prioritize multiple inputs and encode them into a binary output.
Explanation of the given circuit:
In the given circuit, the output A is the OR combination of input signals I2 and I3, which means A = I2 + I3. The output B is the AND combination of input signals I2 and I1, along with I3, which means B = I2*I1 + I3.
Identifying the circuit type:
Based on the given inputs and outputs, it is clear that the circuit is performing encoding based on priority. The output A is dependent on I2 and I3, while the output B is dependent on I2 having higher priority over I1 and I3.
Conclusion:
Therefore, the given circuit corresponds to a Priority Encoder, which encodes multiple input signals into a binary output based on priority. This type of circuit is commonly used in digital systems to handle multiple inputs efficiently and prioritize them based on certain criteria.
The logic circuit of binary adder which is used to add 4-bits binary numbers, requires _________ half adder (s) and ________ full adder(s).- a)1,3
- b)3,1
- c)2,2
- d)4,0
Correct answer is option 'A'. Can you explain this answer?
The logic circuit of binary adder which is used to add 4-bits binary numbers, requires _________ half adder (s) and ________ full adder(s).
a)
1,3
b)
3,1
c)
2,2
d)
4,0
|
|
Debanshi Nair answered |
Logic Circuit of Binary Adder for 4-bit Binary Numbers
The logic circuit of a binary adder is used to add two binary numbers. For adding two 4-bit binary numbers, we need a logic circuit that can perform the addition operation on each bit of the two numbers. The logic circuit of the binary adder for 4-bit binary numbers includes half adder and full adder.
Half Adder
A half adder is a combinational logic circuit that performs the addition of two bits. It has two inputs, A and B, and two outputs, Sum and Carry. The Sum output is the result of adding two bits, and the Carry output is the carry generated during addition. For adding two 4-bit binary numbers, we need four half adders.
Full Adder
A full adder is a combinational logic circuit that performs the addition of three bits. It has three inputs, A, B, and Carry-in, and two outputs, Sum and Carry-out. The Sum output is the result of adding three bits, and the Carry-out output is the carry generated during addition. For adding two 4-bit binary numbers, we need three full adders.
Calculation of Half Adder and Full Adders
For adding two 4-bit binary numbers, we need four half adders to add the first three bits of the two numbers, and three full adders to add the last bit and the carries generated during the addition of the first three bits. Therefore, the logic circuit of binary adder for 4-bit binary numbers requires 1 half adder and 3 full adders.
Conclusion
In conclusion, the logic circuit of binary adder for adding two 4-bit binary numbers requires 1 half adder and 3 full adders. The half adder is used to add the first three bits of the two numbers, and the full adder is used to add the last bit and the carries generated during the addition of the first three bits.
The logic circuit of a binary adder is used to add two binary numbers. For adding two 4-bit binary numbers, we need a logic circuit that can perform the addition operation on each bit of the two numbers. The logic circuit of the binary adder for 4-bit binary numbers includes half adder and full adder.
Half Adder
A half adder is a combinational logic circuit that performs the addition of two bits. It has two inputs, A and B, and two outputs, Sum and Carry. The Sum output is the result of adding two bits, and the Carry output is the carry generated during addition. For adding two 4-bit binary numbers, we need four half adders.
Full Adder
A full adder is a combinational logic circuit that performs the addition of three bits. It has three inputs, A, B, and Carry-in, and two outputs, Sum and Carry-out. The Sum output is the result of adding three bits, and the Carry-out output is the carry generated during addition. For adding two 4-bit binary numbers, we need three full adders.
Calculation of Half Adder and Full Adders
For adding two 4-bit binary numbers, we need four half adders to add the first three bits of the two numbers, and three full adders to add the last bit and the carries generated during the addition of the first three bits. Therefore, the logic circuit of binary adder for 4-bit binary numbers requires 1 half adder and 3 full adders.
Conclusion
In conclusion, the logic circuit of binary adder for adding two 4-bit binary numbers requires 1 half adder and 3 full adders. The half adder is used to add the first three bits of the two numbers, and the full adder is used to add the last bit and the carries generated during the addition of the first three bits.
Which of the following is not a sequential circuit?- a)flip-flop
- b)counter
- c)shift register
- d)multiplexer
Correct answer is option 'D'. Can you explain this answer?
Which of the following is not a sequential circuit?
a)
flip-flop
b)
counter
c)
shift register
d)
multiplexer
|
|
Rajesh Saha answered |
Sequential Circuit
A sequential circuit is a digital circuit that has memory. It means the output of the circuit depends not only on the present input but also on the past input. The sequential circuits can be classified into two categories: Synchronous and Asynchronous circuits.
Synchronous circuits are the circuits that use clocks to synchronize the input and output signals. The input signals are sampled at the rising or falling edge of the clock, and the output signals are updated accordingly. Flip-flops, counters, and shift registers are examples of synchronous circuits.
Asynchronous circuits are the circuits that do not use clocks to synchronize the input and output signals. The output signals are updated whenever the input signals change. Asynchronous circuits are slower and more complex than synchronous circuits.
The Answer
The correct answer to the given question is option 'D', i.e., Multiplexer. A multiplexer is a combinational circuit that selects one input signal out of multiple input signals based on the control signals. A multiplexer does not have any memory or feedback, so it is not a sequential circuit.
Conclusion
In conclusion, a sequential circuit is a digital circuit that has memory, and the output depends on the present and past input signals. Synchronous and asynchronous circuits are two categories of sequential circuits. Flip-flops, counters, and shift registers are examples of synchronous circuits, while multiplexers are not sequential circuits.
A sequential circuit is a digital circuit that has memory. It means the output of the circuit depends not only on the present input but also on the past input. The sequential circuits can be classified into two categories: Synchronous and Asynchronous circuits.
Synchronous circuits are the circuits that use clocks to synchronize the input and output signals. The input signals are sampled at the rising or falling edge of the clock, and the output signals are updated accordingly. Flip-flops, counters, and shift registers are examples of synchronous circuits.
Asynchronous circuits are the circuits that do not use clocks to synchronize the input and output signals. The output signals are updated whenever the input signals change. Asynchronous circuits are slower and more complex than synchronous circuits.
The Answer
The correct answer to the given question is option 'D', i.e., Multiplexer. A multiplexer is a combinational circuit that selects one input signal out of multiple input signals based on the control signals. A multiplexer does not have any memory or feedback, so it is not a sequential circuit.
Conclusion
In conclusion, a sequential circuit is a digital circuit that has memory, and the output depends on the present and past input signals. Synchronous and asynchronous circuits are two categories of sequential circuits. Flip-flops, counters, and shift registers are examples of synchronous circuits, while multiplexers are not sequential circuits.
Which of the following is a decoder IC?- a)7890
- b)8870
- c)4047
- d)4041
Correct answer is option 'B'. Can you explain this answer?
Which of the following is a decoder IC?
a)
7890
b)
8870
c)
4047
d)
4041
|
|
Pooja Patel answered |
8870 is a DTMF decoder circuit, which decodes DTMF tune and produces corresponding output.
Identify the 1 – bit comparator circuit
- a)
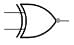
- b)

- c)

- d)

Correct answer is option 'A'. Can you explain this answer?
Identify the 1 – bit comparator circuit


a)

b)

c)

d)

|
|
Pooja Patel answered |
Comparator:
A comparator is a combinational circuit that gives the output in terms of input signals.
It is used to compare numbers and represent their relationship with each other.
It compares the signals as A > B, A < B, and A = B.
1-bit comparator:
A 1-bit comparator circuit is shown below.
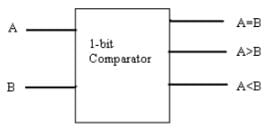
In this circuit, we can compare two input signals
The truth table for the 1-bit comparator is
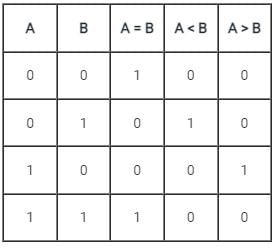
The expression for A = B: A ⊙ B
The expression for A > B: A B̅
The expression for A < B: A̅ B
A comparator is a combinational circuit that gives the output in terms of input signals.
It is used to compare numbers and represent their relationship with each other.
It compares the signals as A > B, A < B, and A = B.
1-bit comparator:
A 1-bit comparator circuit is shown below.

In this circuit, we can compare two input signals
The truth table for the 1-bit comparator is

The expression for A = B: A ⊙ B
The expression for A > B: A B̅
The expression for A < B: A̅ B
The circuit shown in the figure is a –
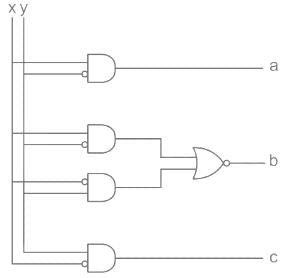
- a)Adder
- b)Comparator
- c)Subtractor
- d)Parity generator
Correct answer is option 'B'. Can you explain this answer?
The circuit shown in the figure is a –


a)
Adder
b)
Comparator
c)
Subtractor
d)
Parity generator
|
|
Pooja Patel answered |
From the given circuit we can find the outputs expression as follows:
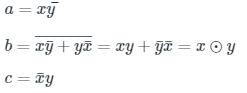
Now, we can observe that
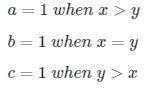
So, the given circuit in question behaves like a comparator circuit.
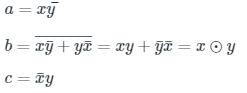
Now, we can observe that
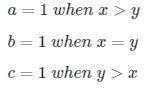
So, the given circuit in question behaves like a comparator circuit.
A digital circuit which compares two numbers A3 A2 A1 A0, B3 B2 B1 B0 is shown in figure. To get output Y = 1, the correct pair of input numbers are
- a)1010, 1010
- b)0101, 0101
- c)0010, 0010
- d)0010, 1011
Correct answer is option 'D'. Can you explain this answer?
A digital circuit which compares two numbers A3 A2 A1 A0, B3 B2 B1 B0 is shown in figure. To get output Y = 1, the correct pair of input numbers are


a)
1010, 1010
b)
0101, 0101
c)
0010, 0010
d)
0010, 1011

|
Pioneer Academy answered |
Y = (A0 ⊕ B0) + (A1 ⊕ B1) + (A2 ⊕ B2) + (A3 ⊕ B3)
Given that output is 1.
To get the output y = 1, all the inputs of OR gate should not be zero.
From the options, A3 A2 A1 A0 = 0010, B3 B2 B1 B0 = 1011 satisfies this condition.
Chapter doubts & questions for Combinational Logic - 6 Months Preparation for GATE Electrical 2025 is part of Electrical Engineering (EE) exam preparation. The chapters have been prepared according to the Electrical Engineering (EE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Electrical Engineering (EE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Combinational Logic - 6 Months Preparation for GATE Electrical in English & Hindi are available as part of Electrical Engineering (EE) exam.
Download more important topics, notes, lectures and mock test series for Electrical Engineering (EE) Exam by signing up for free.
6 Months Preparation for GATE Electrical
795 videos|1417 docs|800 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup