All Exams >
Mechanical Engineering >
6 Months Preparation for GATE Mechanical >
All Questions
All questions of Linear Programming for Mechanical Engineering Exam
Max z = 40x1 + 60x2 s/t: 2x + y ≤ 90x + y ≤ 50x + 2y ≤ 80x, y ≥ 0Find the value of zmax- a) 2400
- b) 2400
- c) alternative optimal
- d) unique
- e) multiple
Correct answer is between ' 2400, 2400'. Can you explain this answer?
Max z = 40x1 + 60x2
s/t: 2x + y ≤ 90
x + y ≤ 50
x + 2y ≤ 80
x, y ≥ 0
Find the value of zmax
a)
2400
b)
2400
c)
alternative optimal
d)
unique
e)
multiple
|
|
Rashi Chauhan answered |
Explanation:
Objective Function:
- Max z = 40x1 + 60x2
Constraints:
1. 2x + y ≤ 90
2. x + y ≤ 50
3. x + 2y ≤ 80
4. x, y ≥ 0
Analysis:
- To find the maximum value of z, we need to optimize the objective function while satisfying all the given constraints.
- The given constraints form a feasible region in the x-y plane.
- By solving the system of inequalities, we can identify the feasible region and determine the corner points.
Corner Points:
- A: (0, 0)
- B: (40, 0)
- C: (20, 30)
- D: (0, 40)
Optimal Solution:
- By evaluating the objective function at each corner point, we find that the maximum value of z (zmax) occurs at point C (20, 30).
- Substitute x = 20 and y = 30 into the objective function: zmax = 40(20) + 60(30) = 2400
Therefore, the correct answer is 2400.
Objective Function:
- Max z = 40x1 + 60x2
Constraints:
1. 2x + y ≤ 90
2. x + y ≤ 50
3. x + 2y ≤ 80
4. x, y ≥ 0
Analysis:
- To find the maximum value of z, we need to optimize the objective function while satisfying all the given constraints.
- The given constraints form a feasible region in the x-y plane.
- By solving the system of inequalities, we can identify the feasible region and determine the corner points.
Corner Points:
- A: (0, 0)
- B: (40, 0)
- C: (20, 30)
- D: (0, 40)
Optimal Solution:
- By evaluating the objective function at each corner point, we find that the maximum value of z (zmax) occurs at point C (20, 30).
- Substitute x = 20 and y = 30 into the objective function: zmax = 40(20) + 60(30) = 2400
Therefore, the correct answer is 2400.
Consider the following LPPMinimize z = 5x1 + 7x2 + x3s/t: 2x1 − x2 + 4x3 ≤ 10x1 , x2 , x3 ≥ 0The solution for the above LPP is- a) unbounded
- b) unique
- c) no solution
- d) infinitely many
Correct answer is option 'A'. Can you explain this answer?
Consider the following LPP
Minimize z = 5x1 + 7x2 + x3
s/t: 2x1 − x2 + 4x3 ≤ 10
x1 , x2 , x3 ≥ 0
The solution for the above LPP is
a)
unbounded
b)
unique
c)
no solution
d)
infinitely many
|
|
Neha Joshi answered |
Standard form:
z − 5x1 − 7x2 − x3 = 0
2x1 − x2 + 4x3 + s1 = 10
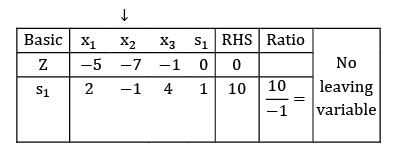
The solution for the LPP isMax z = 3x1 + 2x2s/t: 2x1 + 3x2 ≤ 303x1 + 2x2 ≤ 24x1 + x2 ≥ 3x1 , x2 ≥ 0- a) Unique optimal
- b) Alternate optimal
- c) Degenerate
- d) Unbounded
Correct answer is option 'B'. Can you explain this answer?
The solution for the LPP is
Max z = 3x1 + 2x2
s/t: 2x1 + 3x2 ≤ 30
3x1 + 2x2 ≤ 24
x1 + x2 ≥ 3
x1 , x2 ≥ 0
a)
Unique optimal
b)
Alternate optimal
c)
Degenerate
d)
Unbounded
|
|
Neha Joshi answered |
Given,
2x1 + 3x2 ≤ 30 (0,10)(15, 0)
3x1 + 2x2 ≤ 24 (0, 12)(8, 0)
x1 + x2 ≥ 3 (0, 3)(3, 0)
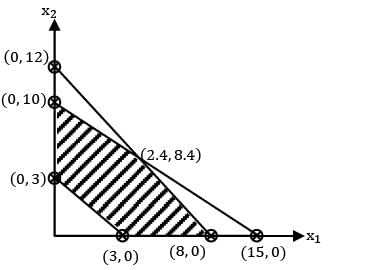
z = 3x1 + 2x2
z(3,0) = 9
z(0,3) = 6
z(0,10) = 20
z(2.4,8.4) = 24
z(8,0) = 24
For a given LPP, Z = 50x1 + 25x2 (max) s/t: 2x1 + 3x2 ≤ 12
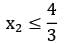 x1 , x2 ≥ 0The type of solution obtained is
x1 , x2 ≥ 0The type of solution obtained is- a) feasible region
- b) optimal solution (unique)
- c) unbounded solution
- d) degenerate solution
Correct answer is option 'B'. Can you explain this answer?
For a given LPP, Z = 50x1 + 25x2 (max) s/t: 2x1 + 3x2 ≤ 12

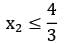
x1 , x2 ≥ 0
The type of solution obtained is
a)
feasible region
b)
optimal solution (unique)
c)
unbounded solution
d)
degenerate solution

|
Cstoppers Instructors answered |
Constraints:
2x1 + 3x2 ≤ 12 (0, 4)(6, 0)
x1 ≤ 4 (x1 = 4)
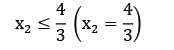
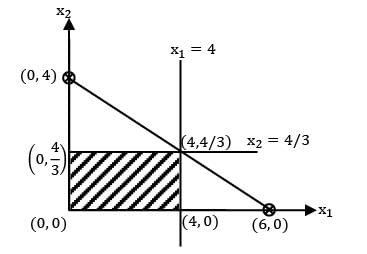
z(0,0) = 0
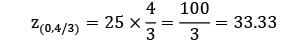
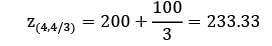
z(4,0) = 200
Consider the problem of assigning four sales persons to four different sales regions as given below. Find the maximum total sales?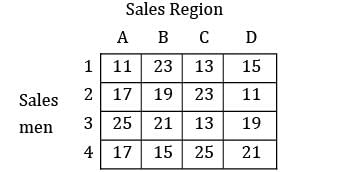 All the values are given in thousands.
All the values are given in thousands.- a) 92
- b) 92
Correct answer is between ' 92, 92'. Can you explain this answer?
Consider the problem of assigning four sales persons to four different sales regions as given below. Find the maximum total sales?

All the values are given in thousands.
a)
92
b)
92
|
|
Sarita Yadav answered |
The given problem is maximization problem. Hungarian algorithm is applicable to only minimization problem so, convert the problem into minimization by subtracting all the elements from max element.
Max element is ‘25’
Loss matrix:
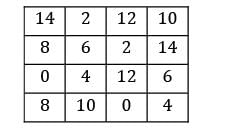
i) Row Reduction:
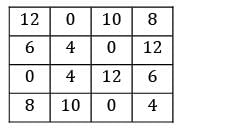
ii) Column Reduction:
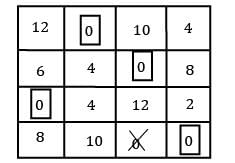
Total sales = 23 + 23 + 25 + 21 = 92
Find optimal assignment cost.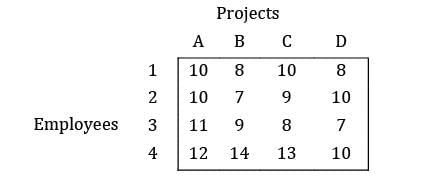
- a) 35
- b) 35
Correct answer is between ' 35, 35'. Can you explain this answer?
Find optimal assignment cost.

a)
35
b)
35

|
Cstoppers Instructors answered |
Row Reduction:
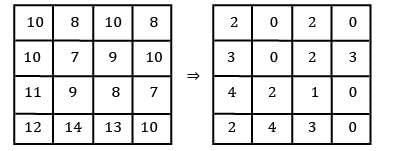
Column Reduction:
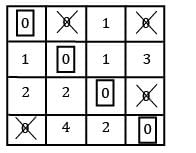
It has multiple solutions TC = 10 + 7 + 8 + 10 = 35
Consider the following linear programming problem:Max. Z = 2A + 3B, subject to A + B < 10,="" 4a="" +="" 6b="" />< 30,="" 2a="" +="" b="" />< 17,="" a,="" b="" ≥="" />What can one say about the solution?- a) It may contain alternative optimal
- b) The solution will be unbounded
- c) The solution will be degenerate
- d) It cannot be solved by simplex method
Correct answer is option 'A'. Can you explain this answer?
Consider the following linear programming problem:
Max. Z = 2A + 3B, subject to A + B < 10,="" 4a="" +="" 6b="" />< 30,="" 2a="" +="" b="" />< 17,="" a,="" b="" ≥="" />
What can one say about the solution?
a)
It may contain alternative optimal
b)
The solution will be unbounded
c)
The solution will be degenerate
d)
It cannot be solved by simplex method
|
|
Sanvi Kapoor answered |
When one of the constraint is parallel to objective function i.e., if slopes are equal then the LPP may contain multiple optimal solutions.
Which of the following type of solution is not possible in simplex method?- a) Unbounded solution
- b) Infeasible solution
- c) Degenerate solution
- d) Multiple optimal solution
Correct answer is option 'B'. Can you explain this answer?
Which of the following type of solution is not possible in simplex method?
a)
Unbounded solution
b)
Infeasible solution
c)
Degenerate solution
d)
Multiple optimal solution
|
|
Zoya Sharma answered |
Simplex method can handle only ≤ type constraints so infeasible solution is not possible.
A constraint in equation 5x1 - 3x2 ≤ -5 is converted as, (3x2 + α1) - (5x1 + -s1) = 5
Then 's1' is called as- a)basic variable
- b)artificial variable
- c)surplus variable
- d)non-basic variable
Correct answer is option 'C'. Can you explain this answer?
A constraint in equation 5x1 - 3x2 ≤ -5 is converted as, (3x2 + α1) - (5x1 + -s1) = 5
Then 's1' is called as
Then 's1' is called as
a)
basic variable
b)
artificial variable
c)
surplus variable
d)
non-basic variable

|
Ashwin Kulkarni answered |
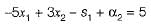
This is used to convert constraint in equation.
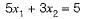
Thus s1 is the surplus variable.
A company produces cups and trays by deep drawing and forming operations. Following data is given on capacity availability and economics of each product.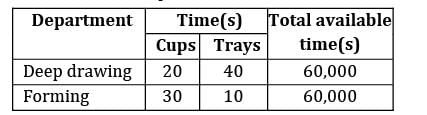 The profit on each cup and tray is given as Rs.40 and Rs.80 respectively. Total daily fixed cost is Rs.90, 000. The maximum net profit per day at the optimum production level is ____________ Rs. [Consider the effect of fixed cost also]Option~(A) 30,000(B) 30,000
The profit on each cup and tray is given as Rs.40 and Rs.80 respectively. Total daily fixed cost is Rs.90, 000. The maximum net profit per day at the optimum production level is ____________ Rs. [Consider the effect of fixed cost also]Option~(A) 30,000(B) 30,000
Correct answer is between ','. Can you explain this answer?
A company produces cups and trays by deep drawing and forming operations. Following data is given on capacity availability and economics of each product.

The profit on each cup and tray is given as Rs.40 and Rs.80 respectively. Total daily fixed cost is Rs.90, 000. The maximum net profit per day at the optimum production level is ____________ Rs. [Consider the effect of fixed cost also]
Option~
(A) 30,000
(B) 30,000

|
Pioneer Academy answered |
Let no. of cups = x
No. of trays = y
Fixed cost = 90,000
Max z = 40x + 80y − 90000
For deep drawing machine 20x + 40y ≤ 60,000
For forming machine 30x + 10y ≤ 60,000
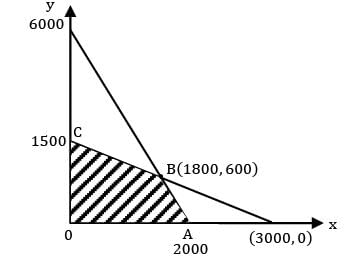
z(0,0) = 0
z(0,1500) = 30,000
z(1800,600) = 30, 000
z(2000,0) = −10,000
Solve the following LPP and identify the type of solutionMax z = 3x1 + 4x2s/t: x1 − x2 ≥ 02.5x1 − x2 ≤ −3x1 , x2 ≥ 0- a) Infeasible solution
- b) Unbounded solution
- c) Degenerate solution
- d) Unique solution
Correct answer is option 'A'. Can you explain this answer?
Solve the following LPP and identify the type of solution
Max z = 3x1 + 4x2
s/t: x1 − x2 ≥ 0
2.5x1 − x2 ≤ −3
x1 , x2 ≥ 0
a)
Infeasible solution
b)
Unbounded solution
c)
Degenerate solution
d)
Unique solution

|
Manish Aggarwal answered |
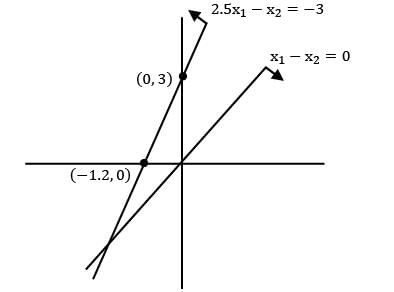
No feasible region
Which one of the following is not the solution method of transportation problems?- a) Hungarian method
- b) Northwest corner method
- c) Least cost method
- d) Vogel's approximation method
Correct answer is option 'A'. Can you explain this answer?
Which one of the following is not the solution method of transportation problems?
a)
Hungarian method
b)
Northwest corner method
c)
Least cost method
d)
Vogel's approximation method
|
|
Zoya Sharma answered |
Hungarian method is used in assignment problem (but remember assignment problem is a special case of transportation problem).
Consider the following profit matrix. Find the max profit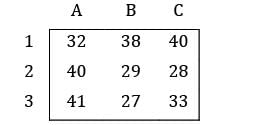
- a) 12
- b) 111
- c) 94
- d) 120
- e) 13
Correct answer is between ' 12, 111'. Can you explain this answer?
Consider the following profit matrix. Find the max profit

a)
12
b)
111
c)
94
d)
120
e)
13

|
Pathways Academy answered |
Row Reduction
Column Reduction
Use straight line method
Total cost = 4 + 3 + 2 + 2 + 2 = 13
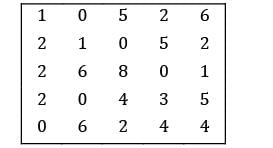
Determine the initial basic feasible solution of the following transportation problem by using VAM.
- a) 791
- b) 791
Correct answer is between ' 791, 791'. Can you explain this answer?
Determine the initial basic feasible solution of the following transportation problem by using VAM.

a)
791
b)
791
|
|
Sanvi Kapoor answered |
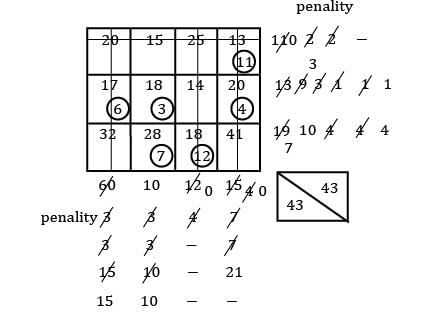
TC = 13 × 11 + 6 × 17 + 3 × 18 + 4 × 20 + 7× 28 + 18 × 12 = 791
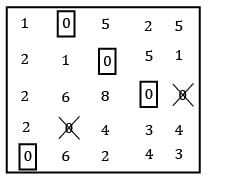
Three workers (P, Q, R) are assigned to 3 machines (M1 , M2 , M3 ) while operator Q cannot be assigned machine M2 . Further, each operator is assigned to one machine and one machine requires only one operator. The operating cost is given for these operators in table below (in Rs). The minimum cost of assignment is ___________ (Rs).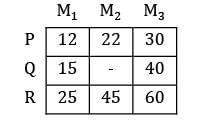
- a) 87
- b) 87
Correct answer is between ' 87, 87'. Can you explain this answer?
Three workers (P, Q, R) are assigned to 3 machines (M1 , M2 , M3 ) while operator Q cannot be assigned machine M2 . Further, each operator is assigned to one machine and one machine requires only one operator. The operating cost is given for these operators in table below (in Rs). The minimum cost of assignment is ___________ (Rs).

a)
87
b)
87
|
|
Avinash Sharma answered |
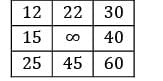
Row Reduction
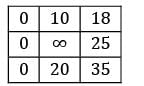
Column Reduction
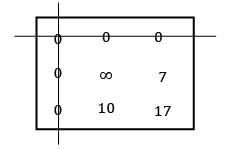
Use straight line method:
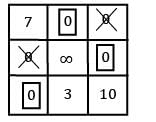
Total minimum cost = 22 + 40 + 25 = 87
Shadow price in linear programming refers to the- a)lowest sales price
- b)maximum cost per item
- c)value assigned to one unit
- d)cost of bought-out items
Correct answer is option 'C'. Can you explain this answer?
Shadow price in linear programming refers to the
a)
lowest sales price
b)
maximum cost per item
c)
value assigned to one unit
d)
cost of bought-out items
|
|
Niharika Iyer answered |
Shadow price in Linear Programming
Shadow price in linear programming refers to the value assigned to one unit of a particular resource or constraint. It is the change in the objective function value per unit increase in the availability of a resource or constraint.
Significance of Shadow Price
The shadow price provides valuable information about the problem and helps in decision-making. It indicates the opportunity cost of using a resource or constraint. It helps in determining the economic feasibility of the problem and identifying the critical resources.
Calculation of Shadow Price
The shadow price can be calculated using the dual simplex method or sensitivity analysis. In the dual simplex method, the shadow price is the negative of the reduced cost of the corresponding dual variable. In sensitivity analysis, the shadow price is the change in the objective function value due to a unit increase in the availability of a resource or constraint.
Interpretation of Shadow Price
A positive shadow price indicates that an increase in the availability of a resource or constraint will increase the objective function value. A negative shadow price indicates that a decrease in the availability of a resource or constraint will increase the objective function value. A zero shadow price indicates that the resource or constraint is not binding.
Conclusion
In conclusion, the shadow price in linear programming refers to the value assigned to one unit of a particular resource or constraint. It provides valuable information about the problem and helps in decision-making. The shadow price can be calculated using the dual simplex method or sensitivity analysis.
Shadow price in linear programming refers to the value assigned to one unit of a particular resource or constraint. It is the change in the objective function value per unit increase in the availability of a resource or constraint.
Significance of Shadow Price
The shadow price provides valuable information about the problem and helps in decision-making. It indicates the opportunity cost of using a resource or constraint. It helps in determining the economic feasibility of the problem and identifying the critical resources.
Calculation of Shadow Price
The shadow price can be calculated using the dual simplex method or sensitivity analysis. In the dual simplex method, the shadow price is the negative of the reduced cost of the corresponding dual variable. In sensitivity analysis, the shadow price is the change in the objective function value due to a unit increase in the availability of a resource or constraint.
Interpretation of Shadow Price
A positive shadow price indicates that an increase in the availability of a resource or constraint will increase the objective function value. A negative shadow price indicates that a decrease in the availability of a resource or constraint will increase the objective function value. A zero shadow price indicates that the resource or constraint is not binding.
Conclusion
In conclusion, the shadow price in linear programming refers to the value assigned to one unit of a particular resource or constraint. It provides valuable information about the problem and helps in decision-making. The shadow price can be calculated using the dual simplex method or sensitivity analysis.
A company produces two products P1 and P2 . The profits per unit of P1 and P2 are Rs.75 and Rs.36 respectively. The market share of the company is 50,000 units of P1 and 80,000 units of P2 .The product P1 require one unit of resource R1 and P2 requires 3 units of resource R1 . The company has a maximum of 60,000 units of R1 . The constraint for resource R1 can be written as- a) x1 ≤ 50,000
- b) x2 ≤ 80,000
- c) x1 + x2 ≤ 60,000
- d) x1 + 3x2 ≤ 60,000
Correct answer is option 'D'. Can you explain this answer?
A company produces two products P1 and P2 . The profits per unit of P1 and P2 are Rs.75 and Rs.36 respectively. The market share of the company is 50,000 units of P1 and 80,000 units of P2 .The product P1 require one unit of resource R1 and P2 requires 3 units of resource R1 . The company has a maximum of 60,000 units of R1 . The constraint for resource R1 can be written as
a)
x1 ≤ 50,000
b)
x2 ≤ 80,000
c)
x1 + x2 ≤ 60,000
d)
x1 + 3x2 ≤ 60,000
|
|
Sarita Yadav answered |
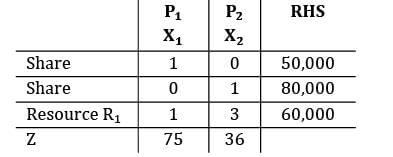
X1 + 3X2 ≤ 60, 000
Consider the following LPPMax z = 2x1 + 10x2s/t: 3x1 + 2x2 ≤ 45x1 + 3x2 ≤ 6x1 + x2 ≤ 10The solution for the above LPP is- a) infeasible
- b) unique optimal
- c) multiple
- d) degenerate
Correct answer is option 'D'. Can you explain this answer?
Consider the following LPP
Max z = 2x1 + 10x2
s/t: 3x1 + 2x2 ≤ 4
5x1 + 3x2 ≤ 6
x1 + x2 ≤ 10
The solution for the above LPP is
a)
infeasible
b)
unique optimal
c)
multiple
d)
degenerate
|
|
Sanvi Kapoor answered |
Given,
Max z = 2x1 + 10x2
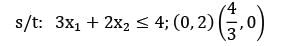
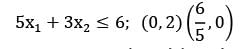
x1 + x2 , ≤ 10; (0, 10)(10, 0)
z(0,0) = 0
z(0,2) = 20∗
z(6/5,0) = 2.4
i) One of the decision variable is zero
ii) There is a redundant constraint present but fully consumed. 3x1 + 2x2 + s1 = 4; s1 = 0
Min z = 4x1 + 6x2s/t: x1 + x2 ≤ 4x1 + 2x2 ≥ 6x1, x2 ≥ 0The type of solution is- a) unique
- b) unbounded
- c) infeasible
- d) multiple optimal
Correct answer is option 'A'. Can you explain this answer?
Min z = 4x1 + 6x2
s/t: x1 + x2 ≤ 4
x1 + 2x2 ≥ 6
x1, x2 ≥ 0
The type of solution is
a)
unique
b)
unbounded
c)
infeasible
d)
multiple optimal
|
|
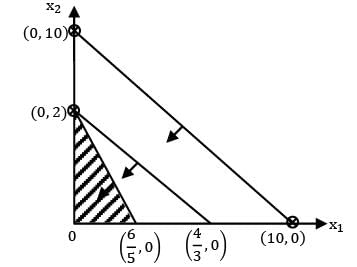
Neha Joshi answered |
Given,
x1 + x2 ≤ 4; (0, 4)(4, 0)
x1 + 2x2 ≥ 6; (0, 3)(6, 0)
only one point:
Z(0,0) = 0
Z(0,3) = 18
Z(2,2) = 20
Z(4,0) = 16
The steps followed for the development of linear programming model are
1. state of problem in the form of a linear programming model
2. determine the decision variables
3. write the objective function
4. develop inequations (or equations) for the constraints.
The correct order is- a)1, 2, 3, 4
- b)2, 1,3, 4
- c)4, 1 2, 3
- d)4, 3 ,2 , 1
Correct answer is option 'C'. Can you explain this answer?
The steps followed for the development of linear programming model are
1. state of problem in the form of a linear programming model
2. determine the decision variables
3. write the objective function
4. develop inequations (or equations) for the constraints.
The correct order is
1. state of problem in the form of a linear programming model
2. determine the decision variables
3. write the objective function
4. develop inequations (or equations) for the constraints.
The correct order is
a)
1, 2, 3, 4
b)
2, 1,3, 4
c)
4, 1 2, 3
d)
4, 3 ,2 , 1
|
|
Aniket Saini answered |
Linear Programming Model Development Process
The correct order of steps followed for the development of a linear programming model is 4, 1, 2, 3. Let's discuss each step in detail:
Step 4: Develop Inequations (or Equations) for the Constraints
- This step involves formulating the constraints that restrict the feasible region of the problem.
- Constraints are the limitations or restrictions that must be adhered to in order to find the optimal solution.
- Constraints can be represented as inequalities (inequations) or equalities (equations).
- These constraints can include limitations on resources, capacity, demand, time, etc.
Step 1: State the Problem in the Form of a Linear Programming Model
- In this step, the problem is transformed into a mathematical model based on linear relationships.
- The decision variables, objective function, and constraints are defined.
- The problem is analyzed to identify the goal or objective that needs to be maximized or minimized.
Step 2: Determine the Decision Variables
- Decision variables are the unknown quantities that need to be optimized in the problem.
- They represent the choices or decisions that the decision-maker can make.
- Decision variables are usually denoted by symbols and can be continuous or discrete.
Step 3: Write the Objective Function
- The objective function represents the goal or objective that needs to be optimized.
- It is a mathematical representation of the quantity that needs to be maximized or minimized.
- The objective function is typically a linear equation, although it can also be nonlinear in some cases.
Correct Order: 4, 1, 2, 3
- The correct order of steps for the development of a linear programming model is 4, 1, 2, 3.
- First, we need to formulate the constraints (inequations or equations) that define the limitations of the problem.
- Then, we state the problem in the form of a linear programming model by defining the objective function and decision variables.
- Finally, we determine the decision variables and write the objective function based on the problem requirements.
Summary:
The correct order for the development of a linear programming model is 4, 1, 2, 3. Constraints are formulated first, followed by stating the problem in the form of a linear programming model, determining the decision variables, and writing the objective function. This sequential process allows for the systematic formulation and optimization of the problem.
The correct order of steps followed for the development of a linear programming model is 4, 1, 2, 3. Let's discuss each step in detail:
Step 4: Develop Inequations (or Equations) for the Constraints
- This step involves formulating the constraints that restrict the feasible region of the problem.
- Constraints are the limitations or restrictions that must be adhered to in order to find the optimal solution.
- Constraints can be represented as inequalities (inequations) or equalities (equations).
- These constraints can include limitations on resources, capacity, demand, time, etc.
Step 1: State the Problem in the Form of a Linear Programming Model
- In this step, the problem is transformed into a mathematical model based on linear relationships.
- The decision variables, objective function, and constraints are defined.
- The problem is analyzed to identify the goal or objective that needs to be maximized or minimized.
Step 2: Determine the Decision Variables
- Decision variables are the unknown quantities that need to be optimized in the problem.
- They represent the choices or decisions that the decision-maker can make.
- Decision variables are usually denoted by symbols and can be continuous or discrete.
Step 3: Write the Objective Function
- The objective function represents the goal or objective that needs to be optimized.
- It is a mathematical representation of the quantity that needs to be maximized or minimized.
- The objective function is typically a linear equation, although it can also be nonlinear in some cases.
Correct Order: 4, 1, 2, 3
- The correct order of steps for the development of a linear programming model is 4, 1, 2, 3.
- First, we need to formulate the constraints (inequations or equations) that define the limitations of the problem.
- Then, we state the problem in the form of a linear programming model by defining the objective function and decision variables.
- Finally, we determine the decision variables and write the objective function based on the problem requirements.
Summary:
The correct order for the development of a linear programming model is 4, 1, 2, 3. Constraints are formulated first, followed by stating the problem in the form of a linear programming model, determining the decision variables, and writing the objective function. This sequential process allows for the systematic formulation and optimization of the problem.
Four workers are required to do four jobs. Time to complete every job is given in the table below Find the minimum cost.
Find the minimum cost.- a) 21
- b) 21
Correct answer is between ' 21, 21'. Can you explain this answer?
Four workers are required to do four jobs. Time to complete every job is given in the table below

Find the minimum cost.
a)
21
b)
21

|
Pioneer Academy answered |
Row Reduction:
Column Reduction:
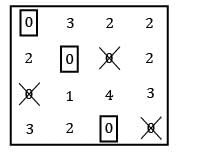
Using straight line method:
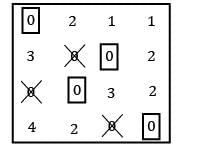
TC = 1 + 10 + 5 + 5 = 21
Consider the following primal LPP. Find dual of the given primal.Max: z = 4x1 + 2x2 + 6x3s/t: 2x1 + 3x2 + 2x3 ≥ 63x1 + 4x2 ≤ 86x1 − 4x2 + x3 ≤ 10s/ t: 2y1 + 3y2 + 6y3 ≥ 43y1 + 4y2 − 4y3 ≥ 22y1 + y3 ≥ 6y1 , y2, y3 ≥ 0s/t: − 2y1 + 3y2 + 6y3 ≥ 4−3y1 + 4y2 − 4y3 ≥ 2−2y1 + y3 ≥ 6y1 , y2, y3 ≥ 02y1 + 3y2 + 6y3 ≤ 43y1 + 4y2 − 4y3 ≤ 22y1 + y3 ≤ 6y1 , y2, y3 ≥ 0s/t: − 2y1 + 3y2 + 6y3 ≤ 4−3y1 + 4y2 − 4y3 ≤ 2−2y1 + y3 ≤ 6y1 , y2, y3 ≥ 0- a) Min w = 6y1 + 8y2 + 10y3
- b) Min w = −6y1 + 8y2 + 10y3
- c) Max w = 6y1 + 8y2 + 10y3
- d) Max w = −6y1 + 8y2 + 10y3
Correct answer is option 'B'. Can you explain this answer?
Consider the following primal LPP. Find dual of the given primal.
Max: z = 4x1 + 2x2 + 6x3
s/t: 2x1 + 3x2 + 2x3 ≥ 6
3x1 + 4x2 ≤ 8
6x1 − 4x2 + x3 ≤ 10
s/ t: 2y1 + 3y2 + 6y3 ≥ 4
3y1 + 4y2 − 4y3 ≥ 2
2y1 + y3 ≥ 6
y1 , y2, y3 ≥ 0
s/t: − 2y1 + 3y2 + 6y3 ≥ 4
−3y1 + 4y2 − 4y3 ≥ 2
−2y1 + y3 ≥ 6
y1 , y2, y3 ≥ 0
2y1 + 3y2 + 6y3 ≤ 4
3y1 + 4y2 − 4y3 ≤ 2
2y1 + y3 ≤ 6
y1 , y2, y3 ≥ 0
s/t: − 2y1 + 3y2 + 6y3 ≤ 4
−3y1 + 4y2 − 4y3 ≤ 2
−2y1 + y3 ≤ 6
y1 , y2, y3 ≥ 0
a)
Min w = 6y1 + 8y2 + 10y3
b)
Min w = −6y1 + 8y2 + 10y3
c)
Max w = 6y1 + 8y2 + 10y3
d)
Max w = −6y1 + 8y2 + 10y3
|
|
Sarita Yadav answered |
zmax = 4x1 + 2x2 + 6x3
s/t: 2x1 + 3x2 + 2x3 ≥ 6
−2x1 − 3x2 − 2x3 ≤ −6
3x1 + 4x2 ≤ 8
6x1 − 4x2 + x3 ≤ 10
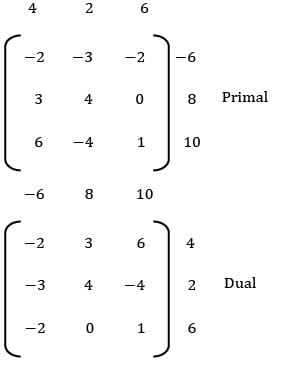
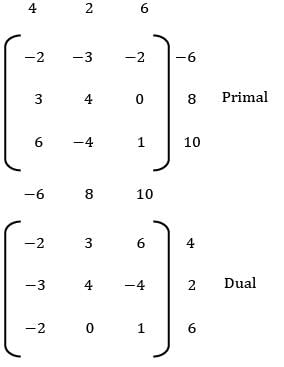
Dual:
Min: w = −6y1 + 8y2 + 10y3
s/t: − 2y1 + 3y2 + 6y3 ≥ 4
−3y1 + 4y2 − 4y3 ≥ 2
−2y1 + y3 ≥ 6
y1 , y2 , y3 ≥ 0
Find the initial basic feasible solution using VAM method.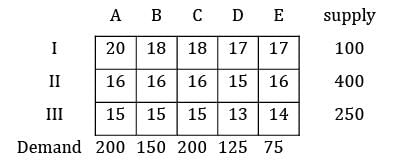
- a) 11625
- b) 11625
Correct answer is option ''. Can you explain this answer?
Find the initial basic feasible solution using VAM method.

a)
11625
b)
11625
|
|
Zoya Sharma answered |
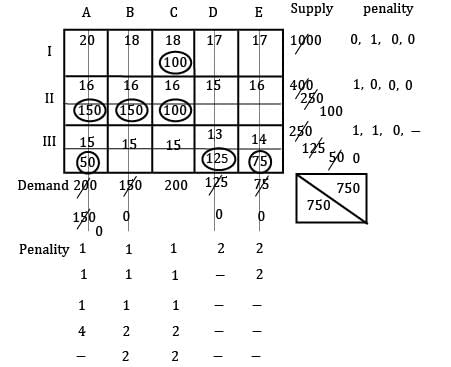
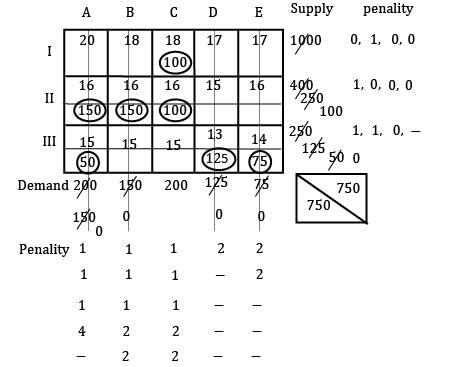
TC = 18 × 100 + 150 × 16 + 150 × 16 + 16× 100 + 15 × 50 + 125 × 13 + 14 × 75
= 11, 625 Rs.
Find the maximum value of the objective function z = 4x + 6y where x ≥ 0 and y ≥ 0, subject to the constraints
- x + y ≤ 11
x + y ≤ 27
2x + 5y ≤ 90- a)66
- b)116
- c)132
- d)108
Correct answer is option 'C'. Can you explain this answer?
Find the maximum value of the objective function z = 4x + 6y where x ≥ 0 and y ≥ 0, subject to the constraints
- x + y ≤ 11
x + y ≤ 27
2x + 5y ≤ 90
- x + y ≤ 11
x + y ≤ 27
2x + 5y ≤ 90
a)
66
b)
116
c)
132
d)
108

|
Aarav Chauhan answered |
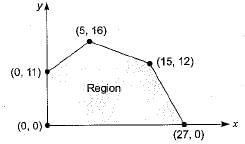
At (0,0): z = 4(0) + 6(0) = 0
At (0, 11): z = 4(0)+ 6(11) = 66
At (5, 16): z = 4(5)+ 6(16) = 116
At (15, 12): z = 4(15) + 6(12) = 132
At (27,0): z = 4(27)+ 6(0) = 108
Consider the given problem. Find the total cost of transportation using N-W method.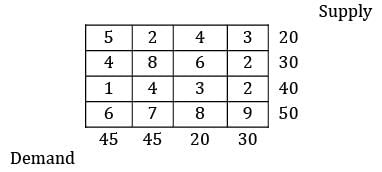
- a) 830
- b) 830
Correct answer is between ' 830, 830'. Can you explain this answer?
Consider the given problem. Find the total cost of transportation using N-W method.

a)
830
b)
830

|
Cstoppers Instructors answered |
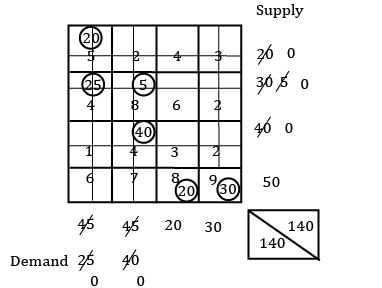
TC = 20 × 5 + 25 × 4 + 5 × 8 + 4 × 40 + 8× 20 + 9 × 30
= 830
The linear programming is used for optimization problems which satisfy the following conditions:
1. Objective function is expressed as a linear function of variables.
2. Resources are unlimited.
3. The decision variables are interrelated and non-negative.Which of these statements is/are correct?- a)1,2 and 3
- b)2 and 3 only
- c)1 only
- d)1 and 3 only
Correct answer is option 'D'. Can you explain this answer?
The linear programming is used for optimization problems which satisfy the following conditions:
1. Objective function is expressed as a linear function of variables.
2. Resources are unlimited.
3. The decision variables are interrelated and non-negative.
1. Objective function is expressed as a linear function of variables.
2. Resources are unlimited.
3. The decision variables are interrelated and non-negative.
Which of these statements is/are correct?
a)
1,2 and 3
b)
2 and 3 only
c)
1 only
d)
1 and 3 only

|
Kavya Mehta answered |
LP is used for optimization problems having limited resource. Unlimited resources have nothing to do with optimization.
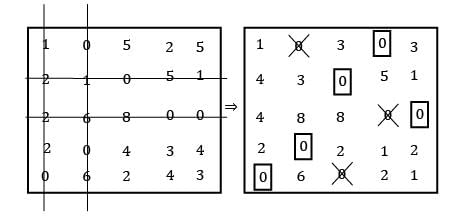
Consider the following problem A cost matrix is given, find the minimum total cost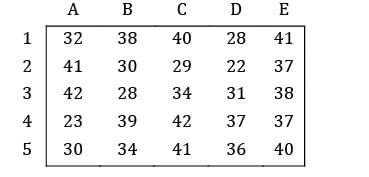
- a) 148
- b) 148
Correct answer is between ' 148, 148'. Can you explain this answer?
Consider the following problem A cost matrix is given, find the minimum total cost

a)
148
b)
148

|
Cstoppers Instructors answered |
i) Row Reduction:
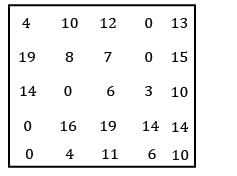
ii) Column Reduction:
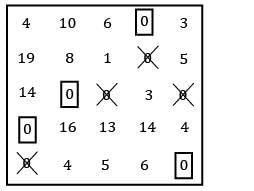
No zero available for allocation ⇒ use straight line method.
TC = 28 + 29 + 28 + 23 + 40 = 148
In a transportation problem rows are the supply points and columns are the demand points. If total supply is less than total demand then- a) dummy column should be added
- b) dummy row should be added
- c) no need to add row or column
- d) either row or column can be added
Correct answer is option 'B'. Can you explain this answer?
In a transportation problem rows are the supply points and columns are the demand points. If total supply is less than total demand then
a)
dummy column should be added
b)
dummy row should be added
c)
no need to add row or column
d)
either row or column can be added

|
Rithika Kaur answered |
Explanation:
Supply and Demand Discrepancy in Transportation Problems
Supply and demand in a transportation problem are represented by rows (supply points) and columns (demand points) respectively. When the total supply is less than the total demand, it creates a discrepancy that needs to be addressed.
Adding a Dummy Row
- When the total supply is less than the total demand in a transportation problem, a dummy row should be added.
- This dummy row helps to balance out the shortage in supply by introducing additional supply points to meet the demand requirements.
- By adding a dummy row, the transportation problem can be solved effectively, ensuring that all demand points are met.
Importance of Adding a Dummy Row
- Adding a dummy row helps in maintaining the balance between supply and demand in the transportation problem.
- It ensures that all demand points are satisfied, even when there is a shortage of supply.
- The dummy row acts as a placeholder for additional supply points, helping to optimize the transportation process.
Conclusion
In conclusion, when the total supply is less than the total demand in a transportation problem, adding a dummy row is the most appropriate solution. This approach ensures that the transportation problem can be solved efficiently, meeting all demand requirements and maintaining a balance between supply and demand.
Supply and Demand Discrepancy in Transportation Problems
Supply and demand in a transportation problem are represented by rows (supply points) and columns (demand points) respectively. When the total supply is less than the total demand, it creates a discrepancy that needs to be addressed.
Adding a Dummy Row
- When the total supply is less than the total demand in a transportation problem, a dummy row should be added.
- This dummy row helps to balance out the shortage in supply by introducing additional supply points to meet the demand requirements.
- By adding a dummy row, the transportation problem can be solved effectively, ensuring that all demand points are met.
Importance of Adding a Dummy Row
- Adding a dummy row helps in maintaining the balance between supply and demand in the transportation problem.
- It ensures that all demand points are satisfied, even when there is a shortage of supply.
- The dummy row acts as a placeholder for additional supply points, helping to optimize the transportation process.
Conclusion
In conclusion, when the total supply is less than the total demand in a transportation problem, adding a dummy row is the most appropriate solution. This approach ensures that the transportation problem can be solved efficiently, meeting all demand requirements and maintaining a balance between supply and demand.
Which of the following statements are true?I. Simplex method can handle only ≤ type constraintsII. Simplex method can be applied only when the number of decision variables are ≥ 3III. Simplex method can be applied to only maximization problems- a) I & III
- b) I, II & III
- c) Only I
- d) I & II
Correct answer is option 'C'. Can you explain this answer?
Which of the following statements are true?
I. Simplex method can handle only ≤ type constraints
II. Simplex method can be applied only when the number of decision variables are ≥ 3
III. Simplex method can be applied to only maximization problems
a)
I & III
b)
I, II & III
c)
Only I
d)
I & II

|
Partho Jain answered |
Simplex Method Constraints
- Statement I is true, as the Simplex method can handle only ≤ type constraints. This is because the method is designed to work with linear programming problems where the constraints are in the form of inequalities.
Number of Decision Variables
- Statement II is false. The Simplex method can be applied to problems with any number of decision variables, not just when the number is greater than or equal to 3. The method is a powerful tool for solving linear programming problems regardless of the number of variables involved.
Objective Function Type
- Statement III is false. The Simplex method can be applied to both maximization and minimization problems. It is not limited to maximization problems only. The method can optimize the objective function by moving through feasible solutions to reach the optimal solution.
Therefore, the correct statements are I and II. The Simplex method is a widely used algorithm for solving linear programming problems with constraints in the form of ≤, =, or ≥ and can handle problems with any number of decision variables. Additionally, it can optimize both maximization and minimization objective functions.
- Statement I is true, as the Simplex method can handle only ≤ type constraints. This is because the method is designed to work with linear programming problems where the constraints are in the form of inequalities.
Number of Decision Variables
- Statement II is false. The Simplex method can be applied to problems with any number of decision variables, not just when the number is greater than or equal to 3. The method is a powerful tool for solving linear programming problems regardless of the number of variables involved.
Objective Function Type
- Statement III is false. The Simplex method can be applied to both maximization and minimization problems. It is not limited to maximization problems only. The method can optimize the objective function by moving through feasible solutions to reach the optimal solution.
Therefore, the correct statements are I and II. The Simplex method is a widely used algorithm for solving linear programming problems with constraints in the form of ≤, =, or ≥ and can handle problems with any number of decision variables. Additionally, it can optimize both maximization and minimization objective functions.
In case of solution of a two variable linear programming problems by graphical method, one constraint line comes parallel to the objective function line. Then the problem will have- a)infeasible solution
- b)unbounded solution
- c)degenerate solution
- d)infinite number of optimal solutions
Correct answer is option 'D'. Can you explain this answer?
In case of solution of a two variable linear programming problems by graphical method, one constraint line comes parallel to the objective function line. Then the problem will have
a)
infeasible solution
b)
unbounded solution
c)
degenerate solution
d)
infinite number of optimal solutions
|
|
Sinjini Nambiar answered |
Solution:
When solving a two-variable linear programming problem by graphical method, if one of the constraint lines is parallel to the objective function line, then the problem will have an infinite number of optimal solutions.
Explanation:
To understand why this is the case, let's consider the following example of a two-variable linear programming problem:
Maximize Z = 3x + 2y
Subject to:
2x + y ≤ 10
3x + y ≥ 12
x, y ≥ 0
We can graph the two constraint lines and the objective function line on the same coordinate plane as shown below:

As we can see, the constraint line 3x + y = 12 is parallel to the objective function line Z = 3x + 2y. This means that any point on the constraint line will have the same objective function value of Z = 12.
Since the feasible region of the problem is bounded (i.e., it is a polygon), there must be at least one corner point that is optimal. However, any corner point that lies on the constraint line 3x + y = 12 will be optimal since it has the same objective function value as any other point on that line.
Therefore, the problem has an infinite number of optimal solutions, all of which lie on the constraint line 3x + y = 12.
Conclusion:
When one of the constraint lines is parallel to the objective function line in a two-variable linear programming problem solved by graphical method, the problem will have an infinite number of optimal solutions.
When solving a two-variable linear programming problem by graphical method, if one of the constraint lines is parallel to the objective function line, then the problem will have an infinite number of optimal solutions.
Explanation:
To understand why this is the case, let's consider the following example of a two-variable linear programming problem:
Maximize Z = 3x + 2y
Subject to:
2x + y ≤ 10
3x + y ≥ 12
x, y ≥ 0
We can graph the two constraint lines and the objective function line on the same coordinate plane as shown below:

As we can see, the constraint line 3x + y = 12 is parallel to the objective function line Z = 3x + 2y. This means that any point on the constraint line will have the same objective function value of Z = 12.
Since the feasible region of the problem is bounded (i.e., it is a polygon), there must be at least one corner point that is optimal. However, any corner point that lies on the constraint line 3x + y = 12 will be optimal since it has the same objective function value as any other point on that line.
Therefore, the problem has an infinite number of optimal solutions, all of which lie on the constraint line 3x + y = 12.
Conclusion:
When one of the constraint lines is parallel to the objective function line in a two-variable linear programming problem solved by graphical method, the problem will have an infinite number of optimal solutions.
Which one of the following is true in case of simplex method of linear programming?- a)The constants of constraints equation may be positive or negative
- b)Inequalities are not converted into equations
- c)It cannot be used for two-variable problems
- d)The simplex algorithm is an iterative procedure
Correct answer is option 'D'. Can you explain this answer?
Which one of the following is true in case of simplex method of linear programming?
a)
The constants of constraints equation may be positive or negative
b)
Inequalities are not converted into equations
c)
It cannot be used for two-variable problems
d)
The simplex algorithm is an iterative procedure
|
|
Prateek Mukherjee answered |
The correct answer is option 'D': The simplex algorithm is an iterative procedure.
The simplex method is a widely used algorithm for solving linear programming problems. It was developed by George Dantzig in the late 1940s and has since become a fundamental tool in optimization theory and operations research.
Iterative Procedure:
The simplex algorithm is an iterative procedure, meaning it applies a set of steps repeatedly until a solution is found or a specified stopping criterion is met. It starts with an initial feasible solution and then iteratively improves the solution until an optimal solution is reached.
Steps of the Simplex Method:
1. Formulate the linear programming problem in standard form, which involves writing the objective function and the constraints as a system of linear equations or inequalities.
2. Identify an initial feasible solution by introducing slack or surplus variables to convert the inequalities into equations.
3. Choose an entering variable, which is a non-basic variable that can be increased to improve the objective function value.
4. Choose a leaving variable, which is a basic variable that can be decreased to maintain feasibility.
5. Update the basic and non-basic variables using a pivot operation, which essentially swaps the entering and leaving variables.
6. Repeat steps 3-5 until an optimal solution is reached, i.e., no non-basic variable can be increased to further improve the objective function value.
7. The final solution will have all non-basic variables set to zero, and the values of the basic variables represent the optimal solution.
Advantages of the Simplex Method:
- The simplex algorithm is efficient and can solve linear programming problems with a large number of variables and constraints.
- It guarantees convergence to an optimal solution if one exists.
- It can handle problems with both equality and inequality constraints.
- It provides sensitivity analysis, allowing decision-makers to understand how changes in the problem parameters affect the optimal solution.
Limitations of the Simplex Method:
- The simplex method may not terminate if the problem is unbounded, meaning there is no upper limit on the objective function value.
- It may also fail to converge if the problem is degenerate, meaning there are multiple optimal solutions.
- The simplex method can become computationally expensive for problems with a large number of variables and constraints.
In conclusion, the simplex algorithm is an iterative procedure used to solve linear programming problems. It is a powerful tool for optimization and can handle problems with both equality and inequality constraints. However, it may have limitations in terms of termination and computational complexity for certain problem types.
The simplex method is a widely used algorithm for solving linear programming problems. It was developed by George Dantzig in the late 1940s and has since become a fundamental tool in optimization theory and operations research.
Iterative Procedure:
The simplex algorithm is an iterative procedure, meaning it applies a set of steps repeatedly until a solution is found or a specified stopping criterion is met. It starts with an initial feasible solution and then iteratively improves the solution until an optimal solution is reached.
Steps of the Simplex Method:
1. Formulate the linear programming problem in standard form, which involves writing the objective function and the constraints as a system of linear equations or inequalities.
2. Identify an initial feasible solution by introducing slack or surplus variables to convert the inequalities into equations.
3. Choose an entering variable, which is a non-basic variable that can be increased to improve the objective function value.
4. Choose a leaving variable, which is a basic variable that can be decreased to maintain feasibility.
5. Update the basic and non-basic variables using a pivot operation, which essentially swaps the entering and leaving variables.
6. Repeat steps 3-5 until an optimal solution is reached, i.e., no non-basic variable can be increased to further improve the objective function value.
7. The final solution will have all non-basic variables set to zero, and the values of the basic variables represent the optimal solution.
Advantages of the Simplex Method:
- The simplex algorithm is efficient and can solve linear programming problems with a large number of variables and constraints.
- It guarantees convergence to an optimal solution if one exists.
- It can handle problems with both equality and inequality constraints.
- It provides sensitivity analysis, allowing decision-makers to understand how changes in the problem parameters affect the optimal solution.
Limitations of the Simplex Method:
- The simplex method may not terminate if the problem is unbounded, meaning there is no upper limit on the objective function value.
- It may also fail to converge if the problem is degenerate, meaning there are multiple optimal solutions.
- The simplex method can become computationally expensive for problems with a large number of variables and constraints.
In conclusion, the simplex algorithm is an iterative procedure used to solve linear programming problems. It is a powerful tool for optimization and can handle problems with both equality and inequality constraints. However, it may have limitations in terms of termination and computational complexity for certain problem types.
The mathematical technique used for finding the best use of limited resources of a concern in the optimum manner is referred to as- a)game theory
- b)value analysis
- c)queuing theory
- d)linear programming
Correct answer is option 'D'. Can you explain this answer?
The mathematical technique used for finding the best use of limited resources of a concern in the optimum manner is referred to as
a)
game theory
b)
value analysis
c)
queuing theory
d)
linear programming

|
Milan Saha answered |
Linear Programming
Linear programming is a mathematical technique used to determine the best possible utilization of limited resources to achieve a specific objective. It is widely used in various fields including business, economics, engineering, and manufacturing.
Optimization of Resources
In linear programming, a set of mathematical equations are formulated to represent the constraints and objectives of the problem. The objective function is then optimized subject to these constraints to find the best possible solution. This allows businesses to make informed decisions on how to allocate resources efficiently.
Application in Business
For example, a manufacturing company may use linear programming to determine the optimal production mix of different products given limited resources such as labor, materials, and equipment. By solving the linear programming model, the company can maximize its profits or minimize costs while meeting demand and capacity constraints.
Benefits
Linear programming helps businesses make better decisions by providing a systematic approach to resource allocation. It allows companies to analyze various scenarios and choose the most cost-effective and efficient solution. This can lead to increased productivity, profitability, and overall performance.
Overall, linear programming is a powerful tool for optimizing resources and making informed decisions in a wide range of applications. By utilizing this mathematical technique, businesses can achieve their goals while making the most effective use of limited resources.
Linear programming can be used to solve- a) Assignment problems
- b) Transportation problems
- c) Both A and B
- d) None of the above
Correct answer is option 'C'. Can you explain this answer?
Linear programming can be used to solve
a)
Assignment problems
b)
Transportation problems
c)
Both A and B
d)
None of the above

|
Bibek Mehra answered |
Linear Programming in Problem Solving
Linear programming is a mathematical method used to determine the best possible outcome in a given mathematical model for a set of constraints. It is widely used in various fields to optimize resource allocation and decision-making processes. Two common types of problems that linear programming can solve are assignment problems and transportation problems.
Assignment Problems
Assignment problems involve assigning a set of tasks to a set of resources in the most efficient way possible. Linear programming can be used to optimize this assignment process by minimizing costs or maximizing efficiency. This can be applied in various scenarios such as job assignments, project scheduling, or machine assignments in manufacturing.
Transportation Problems
Transportation problems involve determining the most cost-effective way to transport goods from a set of sources to a set of destinations. Linear programming can be used to optimize transportation routes, minimize transportation costs, and maximize the efficiency of the transportation network. This is commonly used in logistics, supply chain management, and distribution planning.
Both Assignment and Transportation Problems
Linear programming can be used to solve both assignment problems and transportation problems efficiently. By formulating these problems as linear programming models, optimal solutions can be found to allocate resources, assign tasks, or plan transportation routes effectively. This makes linear programming a versatile tool for solving a wide range of optimization problems in different industries.
In conclusion, linear programming can be effectively used to solve both assignment problems and transportation problems by formulating them as mathematical models and applying optimization techniques to find the best possible solutions.
Linear programming is a mathematical method used to determine the best possible outcome in a given mathematical model for a set of constraints. It is widely used in various fields to optimize resource allocation and decision-making processes. Two common types of problems that linear programming can solve are assignment problems and transportation problems.
Assignment Problems
Assignment problems involve assigning a set of tasks to a set of resources in the most efficient way possible. Linear programming can be used to optimize this assignment process by minimizing costs or maximizing efficiency. This can be applied in various scenarios such as job assignments, project scheduling, or machine assignments in manufacturing.
Transportation Problems
Transportation problems involve determining the most cost-effective way to transport goods from a set of sources to a set of destinations. Linear programming can be used to optimize transportation routes, minimize transportation costs, and maximize the efficiency of the transportation network. This is commonly used in logistics, supply chain management, and distribution planning.
Both Assignment and Transportation Problems
Linear programming can be used to solve both assignment problems and transportation problems efficiently. By formulating these problems as linear programming models, optimal solutions can be found to allocate resources, assign tasks, or plan transportation routes effectively. This makes linear programming a versatile tool for solving a wide range of optimization problems in different industries.
In conclusion, linear programming can be effectively used to solve both assignment problems and transportation problems by formulating them as mathematical models and applying optimization techniques to find the best possible solutions.
In an LPP if one of the decision variable is zero then the solution is- a) unique optimal
- b) infeasible
- c) degenerate if the redundant constraint is fully consumed
- d) unbounded
Correct answer is option 'C'. Can you explain this answer?
In an LPP if one of the decision variable is zero then the solution is
a)
unique optimal
b)
infeasible
c)
degenerate if the redundant constraint is fully consumed
d)
unbounded
|
|
Jyoti Deshpande answered |
Explanation:
There are certain implications when one of the decision variables in a Linear Programming Problem (LPP) is zero. Let's break down the answer in detail:
Degenerate Solution:
When a decision variable is zero in an LPP, it may lead to a degenerate solution. A degenerate solution occurs when the redundant constraint is fully consumed, meaning that the constraint involving the zero decision variable no longer plays a role in determining the feasible region. This can result in the degeneracy of the solution.
Redundant Constraint:
The redundant constraint is the one that does not affect the feasible region when removed. When a decision variable is zero, it implies that the corresponding constraint is fully utilized and no longer contributes to defining the feasible region. This can lead to degeneracy in the solution.
Characteristics of Degenerate Solutions:
Degenerate solutions can complicate the optimization process as they may require additional iterations to reach the optimal solution. They can also affect the efficiency of the algorithm used to solve the LPP. Therefore, it is essential to be aware of the presence of degenerate solutions in order to address them effectively.
In conclusion, when a decision variable is zero in an LPP, it can lead to a degenerate solution if the redundant constraint is fully consumed. Understanding the implications of degeneracy is crucial in optimizing the solution to linear programming problems.
In linear programming a basic feasible solution- a)satisfies constraints only
- b)satisfies constraints and non-negativity restrictions
- c)satisfies non-negativity
- d)optimizes the objective function
Correct answer is option 'B'. Can you explain this answer?
In linear programming a basic feasible solution
a)
satisfies constraints only
b)
satisfies constraints and non-negativity restrictions
c)
satisfies non-negativity
d)
optimizes the objective function

|
Milan Ghosh answered |
Basic Feasible Solution in Linear Programming
Basic feasible solutions are important concepts in linear programming as they help in finding optimal solutions to optimization problems. Here's an explanation of what constitutes a basic feasible solution:
Constraints and Non-negativity Restrictions
- A basic feasible solution must satisfy all the constraints of the linear programming problem. This means that the solution must adhere to all the limitations and requirements set by the problem.
- In addition to satisfying the constraints, a basic feasible solution must also satisfy the non-negativity restrictions. This means that all decision variables in the solution must be greater than or equal to zero.
Optimizing the Objective Function
- While a basic feasible solution does not necessarily optimize the objective function, it provides a starting point for finding the optimal solution. By satisfying all constraints and non-negativity restrictions, a basic feasible solution narrows down the search space for the optimal solution.
- The optimal solution is found by further refining the basic feasible solution through techniques such as the simplex method or graphical method. These methods iteratively improve the solution until the optimal values of the decision variables are obtained.
In conclusion, a basic feasible solution in linear programming satisfies both constraints and non-negativity restrictions, setting the foundation for finding the optimal solution to the optimization problem.
Basic feasible solutions are important concepts in linear programming as they help in finding optimal solutions to optimization problems. Here's an explanation of what constitutes a basic feasible solution:
Constraints and Non-negativity Restrictions
- A basic feasible solution must satisfy all the constraints of the linear programming problem. This means that the solution must adhere to all the limitations and requirements set by the problem.
- In addition to satisfying the constraints, a basic feasible solution must also satisfy the non-negativity restrictions. This means that all decision variables in the solution must be greater than or equal to zero.
Optimizing the Objective Function
- While a basic feasible solution does not necessarily optimize the objective function, it provides a starting point for finding the optimal solution. By satisfying all constraints and non-negativity restrictions, a basic feasible solution narrows down the search space for the optimal solution.
- The optimal solution is found by further refining the basic feasible solution through techniques such as the simplex method or graphical method. These methods iteratively improve the solution until the optimal values of the decision variables are obtained.
In conclusion, a basic feasible solution in linear programming satisfies both constraints and non-negativity restrictions, setting the foundation for finding the optimal solution to the optimization problem.
A tie for leaving variables in simplex procedure implies- a)optimality
- b)cycling
- c)no solution
- d)degeneracy
Correct answer is option 'D'. Can you explain this answer?
A tie for leaving variables in simplex procedure implies
a)
optimality
b)
cycling
c)
no solution
d)
degeneracy
|
|
Nitin Joshi answered |
Explanation:
Simplex procedure is an iterative method used to solve linear programming problems. In each iteration of the simplex procedure, a basic feasible solution (BFS) is obtained by setting non-basic variables to zero and solving for basic variables. The BFS is then used to determine the direction of movement towards the optimal solution.
When there are multiple BFS that provide the same optimal solution, the problem is said to be degenerate. In such cases, the simplex procedure may encounter tie situations where two or more non-basic variables have the same reduced cost. This means that the objective function value remains the same as we increase or decrease the value of any of these variables.
Tie situations in the simplex procedure can lead to cycling, where the algorithm keeps revisiting the same BFS without making any progress towards the optimal solution. This can result in an infinite loop, making it impossible to find the optimal solution.
However, leaving variables in the basis during the simplex procedure can help to break ties and prevent cycling. By leaving non-basic variables in the basis, we can introduce more constraints and reduce the number of possible BFS. This can help to ensure that the simplex procedure converges to the optimal solution without cycling.
Therefore, tie situations in the simplex procedure do not necessarily imply optimality, cycling, or no solution. Instead, they indicate degeneracy, which can be resolved by leaving variables in the basis.
Simplex procedure is an iterative method used to solve linear programming problems. In each iteration of the simplex procedure, a basic feasible solution (BFS) is obtained by setting non-basic variables to zero and solving for basic variables. The BFS is then used to determine the direction of movement towards the optimal solution.
When there are multiple BFS that provide the same optimal solution, the problem is said to be degenerate. In such cases, the simplex procedure may encounter tie situations where two or more non-basic variables have the same reduced cost. This means that the objective function value remains the same as we increase or decrease the value of any of these variables.
Tie situations in the simplex procedure can lead to cycling, where the algorithm keeps revisiting the same BFS without making any progress towards the optimal solution. This can result in an infinite loop, making it impossible to find the optimal solution.
However, leaving variables in the basis during the simplex procedure can help to break ties and prevent cycling. By leaving non-basic variables in the basis, we can introduce more constraints and reduce the number of possible BFS. This can help to ensure that the simplex procedure converges to the optimal solution without cycling.
Therefore, tie situations in the simplex procedure do not necessarily imply optimality, cycling, or no solution. Instead, they indicate degeneracy, which can be resolved by leaving variables in the basis.
Which one of the following statements is NOT correct?- a) Assignment model is a special case of a linear programming problem
- b) In queuing models, Poisson arrivals and exponential services are assumed
- c) In transportation problems, the nonsquare matrix is made square by adding a dummy row or a dummy column
- d) In linear programming problems, dual of a dual is a primal
Correct answer is option 'C'. Can you explain this answer?
Which one of the following statements is NOT correct?
a)
Assignment model is a special case of a linear programming problem
b)
In queuing models, Poisson arrivals and exponential services are assumed
c)
In transportation problems, the nonsquare matrix is made square by adding a dummy row or a dummy column
d)
In linear programming problems, dual of a dual is a primal

|
Ashish Chakraborty answered |
Explanation:
Transportation problems:
- In transportation problems, the nonsquare matrix is made square by adding a dummy row or a dummy column.
- This process is known as matrix balancing, where dummy rows or columns are added to make the matrix square.
- The addition of dummy rows or columns ensures that the total supply is equal to the total demand, making it easier to solve the transportation problem.
Correct statement:
- In transportation problems, the nonsquare matrix is made square by adding a dummy row or a dummy column.
Therefore, the statement "In transportation problems, the nonsquare matrix is made square by adding a dummy row or a dummy column" is correct, and not incorrect as mentioned in the question.
Transportation problems:
- In transportation problems, the nonsquare matrix is made square by adding a dummy row or a dummy column.
- This process is known as matrix balancing, where dummy rows or columns are added to make the matrix square.
- The addition of dummy rows or columns ensures that the total supply is equal to the total demand, making it easier to solve the transportation problem.
Correct statement:
- In transportation problems, the nonsquare matrix is made square by adding a dummy row or a dummy column.
Therefore, the statement "In transportation problems, the nonsquare matrix is made square by adding a dummy row or a dummy column" is correct, and not incorrect as mentioned in the question.
The number of basic variables in a simplex method is equal to- a) Number of decision variables
- b) Number of constraints
- c) Total available variables (slack variables plus decision variables)
- d) None of the above
Correct answer is option 'B'. Can you explain this answer?
The number of basic variables in a simplex method is equal to
a)
Number of decision variables
b)
Number of constraints
c)
Total available variables (slack variables plus decision variables)
d)
None of the above
|
|
Nishanth Basu answered |
Explanation:
Number of Basic Variables in Simplex Method
In the simplex method, the number of basic variables is equal to the number of constraints in the linear programming problem. This is because each constraint in the problem corresponds to a basic variable in the simplex method.
Basic Variables vs. Non-Basic Variables
- Basic variables are the variables that are chosen as the basic variables at each iteration of the simplex method.
- Non-basic variables are the remaining variables in the problem that are not chosen as basic variables.
Role of Basic Variables
- Basic variables play a crucial role in the simplex method as they form the basis of the solution.
- The values of the basic variables determine the values of the non-basic variables through the constraints of the linear programming problem.
Number of Decision Variables vs. Number of Constraints
- The number of decision variables in a linear programming problem is not necessarily equal to the number of basic variables in the simplex method.
- The number of constraints, on the other hand, directly corresponds to the number of basic variables in the simplex method.
Therefore, the correct answer to the question is option 'B', as the number of basic variables in the simplex method is equal to the number of constraints in the linear programming problem.
Number of Basic Variables in Simplex Method
In the simplex method, the number of basic variables is equal to the number of constraints in the linear programming problem. This is because each constraint in the problem corresponds to a basic variable in the simplex method.
Basic Variables vs. Non-Basic Variables
- Basic variables are the variables that are chosen as the basic variables at each iteration of the simplex method.
- Non-basic variables are the remaining variables in the problem that are not chosen as basic variables.
Role of Basic Variables
- Basic variables play a crucial role in the simplex method as they form the basis of the solution.
- The values of the basic variables determine the values of the non-basic variables through the constraints of the linear programming problem.
Number of Decision Variables vs. Number of Constraints
- The number of decision variables in a linear programming problem is not necessarily equal to the number of basic variables in the simplex method.
- The number of constraints, on the other hand, directly corresponds to the number of basic variables in the simplex method.
Therefore, the correct answer to the question is option 'B', as the number of basic variables in the simplex method is equal to the number of constraints in the linear programming problem.
A product is manufactured using two raw materials A and B. A is taken on x-axis and B is taken on Y-axis and the LPP is as follows.Zmin = 2A + 3BS⁄t ∶ 0.6 A + 0.3 B ≥ 450.1 A + 0.5B ≥ 25A, B ≥ 0Which of the following statement is correct?- a) Decrease of 3 units in A will cause increase of 2 units in B
- b) Decrease of 3 units in A will cause decrease of 2 units in B
- c) Decrease of 2 units in A will cause increase of 3 units in B
- d) Decrease of 2 units in A will cause decrease of 3 units in B
Correct answer is option 'A'. Can you explain this answer?
A product is manufactured using two raw materials A and B. A is taken on x-axis and B is taken on Y-axis and the LPP is as follows.
Zmin = 2A + 3B
S⁄t ∶ 0.6 A + 0.3 B ≥ 45
0.1 A + 0.5B ≥ 25
A, B ≥ 0
Which of the following statement is correct?
a)
Decrease of 3 units in A will cause increase of 2 units in B
b)
Decrease of 3 units in A will cause decrease of 2 units in B
c)
Decrease of 2 units in A will cause increase of 3 units in B
d)
Decrease of 2 units in A will cause decrease of 3 units in B
|
|
Anjali Shah answered |
Explanation:
Given Linear Programming Problem (LPP):
- Objective function: Zmin = 2A + 3B
- Constraints:
- 0.6A + 0.3B ≥ 45
- 0.1A + 0.5B ≥ 25
- A, B ≥ 0
Analysis:
- To find the correct statement, we need to analyze the coefficients of A and B in the objective function and constraints.
Objective Function:
- Coefficient of A: 2
- Coefficient of B: 3
First Constraint:
- Coefficients of A and B are 0.6 and 0.3 respectively.
- To maintain the feasibility of the constraint, an increase in A should be accompanied by a greater increase in B.
Second Constraint:
- Coefficients of A and B are 0.1 and 0.5 respectively.
- To maintain the feasibility of the constraint, an increase in A should be accompanied by a greater increase in B.
Conclusion:
- Since the coefficients of B are greater in both constraints as well as the objective function, a decrease in A will lead to an increase in B.
- Therefore, the correct statement is: Decrease of 3 units in A will cause increase of 2 units in B.
Given Linear Programming Problem (LPP):
- Objective function: Zmin = 2A + 3B
- Constraints:
- 0.6A + 0.3B ≥ 45
- 0.1A + 0.5B ≥ 25
- A, B ≥ 0
Analysis:
- To find the correct statement, we need to analyze the coefficients of A and B in the objective function and constraints.
Objective Function:
- Coefficient of A: 2
- Coefficient of B: 3
First Constraint:
- Coefficients of A and B are 0.6 and 0.3 respectively.
- To maintain the feasibility of the constraint, an increase in A should be accompanied by a greater increase in B.
Second Constraint:
- Coefficients of A and B are 0.1 and 0.5 respectively.
- To maintain the feasibility of the constraint, an increase in A should be accompanied by a greater increase in B.
Conclusion:
- Since the coefficients of B are greater in both constraints as well as the objective function, a decrease in A will lead to an increase in B.
- Therefore, the correct statement is: Decrease of 3 units in A will cause increase of 2 units in B.
In an assignment problem having n facilities and n jobs, what is the number of possible ways of making assignments?- a) nl
- b) n2
- c) 2n
- d) 2n
Correct answer is option 'A'. Can you explain this answer?
In an assignment problem having n facilities and n jobs, what is the number of possible ways of making assignments?
a)
nl
b)
n2
c)
2n
d)
2n
|
|
Asha Basu answered |
Number of Possible Ways of Making Assignments in an Assignment Problem
An assignment problem is a special type of linear programming problem where we have n facilities and n jobs to be assigned to these facilities. The objective is to minimize the total cost of assignments while ensuring that each facility is assigned to only one job and each job is assigned to only one facility. In such a problem, the number of possible ways of making assignments can be calculated as follows:
1. Understanding the Problem Requirements
To calculate the number of possible ways of making assignments, we need to first understand the problem requirements. In an assignment problem, we have n facilities and n jobs, and we need to assign each job to one facility and each facility to one job. Therefore, we need to find the total number of ways in which we can make such assignments.
2. Using the Fundamental Principle of Counting
The fundamental principle of counting states that if there are m ways to perform one task and n ways to perform another task, then there are m x n ways to perform both tasks together. Using this principle, we can calculate the number of possible ways of making assignments in an assignment problem.
Since we have n facilities and n jobs, there are n ways to assign the first job to a facility. Once the first job is assigned to a facility, there are n - 1 ways to assign the second job to a facility (since we cannot assign it to the same facility as the first job). Similarly, there are n - 2 ways to assign the third job to a facility (since we cannot assign it to the same facility as the first two jobs), and so on.
Therefore, the total number of possible ways of making assignments is:
n x (n - 1) x (n - 2) x ... x 2 x 1 = n!
This means that there are n! (n factorial) possible ways of making assignments in an assignment problem, where n is the number of facilities and jobs.
3. Choosing the Correct Option
Out of the given options, option A (n!) is the correct answer since it represents the total number of possible ways of making assignments in an assignment problem with n facilities and n jobs. The other options (n^2, 2n, 2^n) do not provide the correct answer since they do not consider the fundamental principle of counting and the specific requirements of an assignment problem.
An assignment problem is a special type of linear programming problem where we have n facilities and n jobs to be assigned to these facilities. The objective is to minimize the total cost of assignments while ensuring that each facility is assigned to only one job and each job is assigned to only one facility. In such a problem, the number of possible ways of making assignments can be calculated as follows:
1. Understanding the Problem Requirements
To calculate the number of possible ways of making assignments, we need to first understand the problem requirements. In an assignment problem, we have n facilities and n jobs, and we need to assign each job to one facility and each facility to one job. Therefore, we need to find the total number of ways in which we can make such assignments.
2. Using the Fundamental Principle of Counting
The fundamental principle of counting states that if there are m ways to perform one task and n ways to perform another task, then there are m x n ways to perform both tasks together. Using this principle, we can calculate the number of possible ways of making assignments in an assignment problem.
Since we have n facilities and n jobs, there are n ways to assign the first job to a facility. Once the first job is assigned to a facility, there are n - 1 ways to assign the second job to a facility (since we cannot assign it to the same facility as the first job). Similarly, there are n - 2 ways to assign the third job to a facility (since we cannot assign it to the same facility as the first two jobs), and so on.
Therefore, the total number of possible ways of making assignments is:
n x (n - 1) x (n - 2) x ... x 2 x 1 = n!
This means that there are n! (n factorial) possible ways of making assignments in an assignment problem, where n is the number of facilities and jobs.
3. Choosing the Correct Option
Out of the given options, option A (n!) is the correct answer since it represents the total number of possible ways of making assignments in an assignment problem with n facilities and n jobs. The other options (n^2, 2n, 2^n) do not provide the correct answer since they do not consider the fundamental principle of counting and the specific requirements of an assignment problem.
The while solving a LP model graphically, the area bounded by the constraints is called- a)feasible region
- b)infeasible region
- c)unbounded solution
- d)none of the above
Correct answer is option 'A'. Can you explain this answer?
The while solving a LP model graphically, the area bounded by the constraints is called
a)
feasible region
b)
infeasible region
c)
unbounded solution
d)
none of the above
|
|
Soumya Basak answered |
Feasible Region in LP Model
The feasible region is a term used in linear programming to describe the set of all possible solutions to an optimization problem. When solving a linear programming problem graphically, the feasible region is the area bounded by the constraints.
Features of Feasible Region:
1. It is a convex polygon.
2. Every point inside the feasible region satisfies all the constraints.
3. The objective function is optimized at one of the corners of the feasible region.
4. The feasible region can be either bounded or unbounded.
Infeasible Region and Unbounded Solution
An infeasible region is a region that does not contain any feasible solutions. It is the region outside the feasible region, where at least one of the constraints is violated.
An unbounded solution is a solution that can be increased or decreased without limit. It occurs when the objective function can be improved indefinitely in a particular direction. In other words, the feasible region extends infinitely in one or more directions.
Conclusion
In conclusion, the feasible region is the area bounded by the constraints in a linear programming problem. It contains all possible solutions that satisfy the constraints. An infeasible region is a region that does not contain any feasible solutions, while an unbounded solution occurs when the feasible region extends infinitely in one or more directions.
The feasible region is a term used in linear programming to describe the set of all possible solutions to an optimization problem. When solving a linear programming problem graphically, the feasible region is the area bounded by the constraints.
Features of Feasible Region:
1. It is a convex polygon.
2. Every point inside the feasible region satisfies all the constraints.
3. The objective function is optimized at one of the corners of the feasible region.
4. The feasible region can be either bounded or unbounded.
Infeasible Region and Unbounded Solution
An infeasible region is a region that does not contain any feasible solutions. It is the region outside the feasible region, where at least one of the constraints is violated.
An unbounded solution is a solution that can be increased or decreased without limit. It occurs when the objective function can be improved indefinitely in a particular direction. In other words, the feasible region extends infinitely in one or more directions.
Conclusion
In conclusion, the feasible region is the area bounded by the constraints in a linear programming problem. It contains all possible solutions that satisfy the constraints. An infeasible region is a region that does not contain any feasible solutions, while an unbounded solution occurs when the feasible region extends infinitely in one or more directions.
The primal of a LP problem is maximization of objective function with 6 variables and 2 constraints. Which of the following correspond to the dual of the problem stated?1. It has 2 variables and 6 constraints2. It has 6 variables and 2 constraints3. Maximization of objective function4. Minimization of objective functionSelect the correct answer using the codes given below- a) 1 and 3
- b) 1 and 4
- c) 2 and 3
- d) 2 and 4
Correct answer is option 'B'. Can you explain this answer?
The primal of a LP problem is maximization of objective function with 6 variables and 2 constraints. Which of the following correspond to the dual of the problem stated?
1. It has 2 variables and 6 constraints
2. It has 6 variables and 2 constraints
3. Maximization of objective function
4. Minimization of objective function
Select the correct answer using the codes given below
a)
1 and 3
b)
1 and 4
c)
2 and 3
d)
2 and 4
|
|
Dhruv Dasgupta answered |
Explanation:
Dual of the LP problem:
- The dual of the LP problem involves switching the roles of variables and constraints.
- In this case, since the primal problem has 6 variables and 2 constraints, the dual will have 2 variables and 6 constraints.
Correspondence to the dual:
- Option 1 correctly corresponds to the dual with 2 variables and 6 constraints.
- Option 4 corresponds to the minimization of the objective function in the dual problem.
Therefore, the correct answer is option B which includes both 1 and 4.
Dual of the LP problem:
- The dual of the LP problem involves switching the roles of variables and constraints.
- In this case, since the primal problem has 6 variables and 2 constraints, the dual will have 2 variables and 6 constraints.
Correspondence to the dual:
- Option 1 correctly corresponds to the dual with 2 variables and 6 constraints.
- Option 4 corresponds to the minimization of the objective function in the dual problem.
Therefore, the correct answer is option B which includes both 1 and 4.
Which of the following is a correct expression for an objective function in an LPP?- a) z = 2x1 + 3x2 + 5x1 ∙ x2
- b) z = x12 + 2x2
- c) z = 3x1 + 10x2
- d) z = 6x13 + 5x12 + 3x2
Correct answer is option 'C'. Can you explain this answer?
Which of the following is a correct expression for an objective function in an LPP?
a)
z = 2x1 + 3x2 + 5x1 ∙ x2
b)
z = x12 + 2x2
c)
z = 3x1 + 10x2
d)
z = 6x13 + 5x12 + 3x2
|
|
Aniket Saini answered |
Objective Function in Linear Programming:
The objective function in a linear programming problem represents the quantity that needs to be maximized or minimized. It is typically denoted by 'z' and is a linear combination of decision variables with coefficients representing the contribution of each variable to the overall objective.
Correct Expression for Objective Function:
The correct expression for an objective function in a Linear Programming Problem is typically a linear combination of decision variables. In this case, the correct expression given is:
z = 3x1 + 10x2
Here, 'z' represents the objective function to be optimized, 'x1' and 'x2' are the decision variables, and 3 and 10 are the coefficients of these variables respectively. This expression indicates that the objective function is a linear combination of 'x1' and 'x2' with specific coefficients attached to each variable.
Explanation:
- The objective function in a Linear Programming Problem is crucial as it defines the goal of the optimization process.
- In the given expression, 'z = 3x1 + 10x2', the coefficients 3 and 10 indicate the contribution or weight of each decision variable towards the objective.
- By maximizing or minimizing this objective function subject to certain constraints, optimal values of the decision variables 'x1' and 'x2' can be determined.
- The objective function plays a key role in guiding the optimization algorithm towards finding the best solution that satisfies all constraints while optimizing the objective.
In conclusion, the correct expression for an objective function in a Linear Programming Problem is a linear combination of decision variables, with specific coefficients representing the contribution of each variable towards the overall objective.
The objective function in a linear programming problem represents the quantity that needs to be maximized or minimized. It is typically denoted by 'z' and is a linear combination of decision variables with coefficients representing the contribution of each variable to the overall objective.
Correct Expression for Objective Function:
The correct expression for an objective function in a Linear Programming Problem is typically a linear combination of decision variables. In this case, the correct expression given is:
z = 3x1 + 10x2
Here, 'z' represents the objective function to be optimized, 'x1' and 'x2' are the decision variables, and 3 and 10 are the coefficients of these variables respectively. This expression indicates that the objective function is a linear combination of 'x1' and 'x2' with specific coefficients attached to each variable.
Explanation:
- The objective function in a Linear Programming Problem is crucial as it defines the goal of the optimization process.
- In the given expression, 'z = 3x1 + 10x2', the coefficients 3 and 10 indicate the contribution or weight of each decision variable towards the objective.
- By maximizing or minimizing this objective function subject to certain constraints, optimal values of the decision variables 'x1' and 'x2' can be determined.
- The objective function plays a key role in guiding the optimization algorithm towards finding the best solution that satisfies all constraints while optimizing the objective.
In conclusion, the correct expression for an objective function in a Linear Programming Problem is a linear combination of decision variables, with specific coefficients representing the contribution of each variable towards the overall objective.
Which one of the following is true in case of simplex method of linear programming?Iterative solution: The steps keep on repeating until we get an optimal solution.- a) The constants of constraints equation may be positive or negative
- b) Inequalities are not converted into equations
- c) It cannot be used for two-variable problems
- d) The simplex algorithm is an iterative procedure
Correct answer is option 'D'. Can you explain this answer?
Which one of the following is true in case of simplex method of linear programming?
Iterative solution: The steps keep on repeating until we get an optimal solution.
a)
The constants of constraints equation may be positive or negative
b)
Inequalities are not converted into equations
c)
It cannot be used for two-variable problems
d)
The simplex algorithm is an iterative procedure

|
Lakshmi Datta answered |
Simplex Method in Linear Programming
Iterative Solution
- The simplex method is an iterative procedure where the steps are repeated until an optimal solution is reached.
- At each iteration, the algorithm moves from one basic feasible solution to another, improving the objective function value each time.
Constants of Constraints Equation
- The constants of the constraints equation may be positive or negative, as the simplex method can handle both types of coefficients.
Inequalities to Equations
- In the simplex method, inequalities are typically converted into equations by introducing slack, surplus, or artificial variables.
- This transformation allows the algorithm to work with equations instead of inequalities.
Two-Variable Problems
- The simplex method can be used for problems with any number of variables, including two-variable problems.
- It is a powerful tool for solving linear programming problems with multiple decision variables.
Conclusion
- The simplex algorithm is an iterative procedure that can handle both positive and negative constants in constraints equations, convert inequalities into equations, and be used for problems with any number of variables.
Iterative Solution
- The simplex method is an iterative procedure where the steps are repeated until an optimal solution is reached.
- At each iteration, the algorithm moves from one basic feasible solution to another, improving the objective function value each time.
Constants of Constraints Equation
- The constants of the constraints equation may be positive or negative, as the simplex method can handle both types of coefficients.
Inequalities to Equations
- In the simplex method, inequalities are typically converted into equations by introducing slack, surplus, or artificial variables.
- This transformation allows the algorithm to work with equations instead of inequalities.
Two-Variable Problems
- The simplex method can be used for problems with any number of variables, including two-variable problems.
- It is a powerful tool for solving linear programming problems with multiple decision variables.
Conclusion
- The simplex algorithm is an iterative procedure that can handle both positive and negative constants in constraints equations, convert inequalities into equations, and be used for problems with any number of variables.
Simplex method of solving linear programming problem uses- a)all the points in the feasible region
- b)only the corner points of the feasible region
- c)intermediate points within the infeasible region
- d)only the interior points in the feasible reg
Correct answer is option 'B'. Can you explain this answer?
Simplex method of solving linear programming problem uses
a)
all the points in the feasible region
b)
only the corner points of the feasible region
c)
intermediate points within the infeasible region
d)
only the interior points in the feasible reg
|
|
Sandeep Sengupta answered |
Corner Points
- The simplex method of solving linear programming problems involves determining the optimal solution by moving from one corner point (or vertex) of the feasible region to another.
- The corner points are the intersection points of the constraint lines that define the feasible region.
Feasible Region
- The feasible region is the area in which all constraints of the linear programming problem are satisfied.
- The corner points represent the extreme points of the feasible region.
Optimal Solution
- By evaluating the objective function at each corner point, the simplex method allows us to find the optimal solution.
- The optimal solution is the corner point that maximizes or minimizes the objective function, depending on the problem.
Advantages of Using Corner Points
- The simplex method is efficient because it only considers a finite number of corner points instead of all the points in the feasible region.
- By focusing on the corner points, the simplex method simplifies the problem-solving process and reduces computational complexity.
Therefore, the correct answer is option 'b) only the corner points of the feasible region', as the simplex method specifically utilizes these corner points to find the optimal solution for linear programming problems.
The linear programming is used for optimization problems which satisfy the following conditions:
1. Objective function expressed as a linear function of variables.
2. Resources are unlimited.
3. The decision variables are inter-related and non-negative.
Which of these statements is/are correct?- a)1, 2 and 3
- b)2 and 3 only
- c)1 only
- d)1 and 3 only
Correct answer is option 'D'. Can you explain this answer?
The linear programming is used for optimization problems which satisfy the following conditions:
1. Objective function expressed as a linear function of variables.
2. Resources are unlimited.
3. The decision variables are inter-related and non-negative.
Which of these statements is/are correct?
1. Objective function expressed as a linear function of variables.
2. Resources are unlimited.
3. The decision variables are inter-related and non-negative.
Which of these statements is/are correct?
a)
1, 2 and 3
b)
2 and 3 only
c)
1 only
d)
1 and 3 only

|
Rajdeep Gupta answered |
Linear Programming Conditions for Optimization
1. Objective function as a linear function of variables: In linear programming, the objective function is to be maximized or minimized, and it must be expressed as a linear combination of decision variables. This means that the coefficients of the variables are constants and the variables appear in a linear form.
2. Resources are unlimited: Linear programming assumes that resources such as raw materials, labor, and budget are unlimited. This simplifies the optimization process as there are no constraints on the availability of resources.
3. Inter-related and non-negative decision variables: The decision variables in linear programming are inter-related, meaning that they are connected in a linear manner. Additionally, these variables must be non-negative, which means they cannot take on negative values in the optimization process.
Therefore, the correct statement is option 'D' - 1 and 3 only, as linear programming involves an objective function expressed linearly and non-negative inter-related decision variables, while assuming unlimited resources.
1. Objective function as a linear function of variables: In linear programming, the objective function is to be maximized or minimized, and it must be expressed as a linear combination of decision variables. This means that the coefficients of the variables are constants and the variables appear in a linear form.
2. Resources are unlimited: Linear programming assumes that resources such as raw materials, labor, and budget are unlimited. This simplifies the optimization process as there are no constraints on the availability of resources.
3. Inter-related and non-negative decision variables: The decision variables in linear programming are inter-related, meaning that they are connected in a linear manner. Additionally, these variables must be non-negative, which means they cannot take on negative values in the optimization process.
Therefore, the correct statement is option 'D' - 1 and 3 only, as linear programming involves an objective function expressed linearly and non-negative inter-related decision variables, while assuming unlimited resources.
Which one of the following is the correct statement? In the standard form of a linear programming problem, all constraints are- a) Of less than or equal to type
- b) Of greater or equal to type
- c) In the form of equations
- d) Some constraints are of less than equal to type and some are of greater than equal to type
Correct answer is option 'C'. Can you explain this answer?
Which one of the following is the correct statement? In the standard form of a linear programming problem, all constraints are
a)
Of less than or equal to type
b)
Of greater or equal to type
c)
In the form of equations
d)
Some constraints are of less than equal to type and some are of greater than equal to type

|
Ashwin Gupta answered |
**Correct Statement:**
The correct statement is option 'C': In the standard form of a linear programming problem, all constraints are in the form of equations.
**Explanation:**
Linear programming is a mathematical optimization technique used to determine the best possible outcome in a given mathematical model, given a set of constraints. The standard form of a linear programming problem involves maximizing or minimizing a linear objective function, subject to a set of linear constraints.
In the standard form, the objective function and all constraints must be in the form of equations rather than inequalities. This is because the objective function represents the quantity to be maximized or minimized, and the constraints represent the limitations or restrictions on the variables.
**Reason for Incorrect Options:**
a) Option 'A': Of less than or equal to type
This option is incorrect because linear programming problems may involve constraints of both less than or equal to and greater than or equal to type. However, in the standard form, all constraints are represented as equations.
b) Option 'B': Of greater or equal to type
This option is also incorrect for the same reason as option 'A'. Linear programming problems can have constraints of both types, but in the standard form, they are all represented as equations.
d) Option 'D': Some constraints are of less than equal to type and some are of greater than equal to type
This option is incorrect because, as mentioned earlier, in the standard form, all constraints are represented as equations and not as inequalities of any type.
**Conclusion:**
In the standard form of a linear programming problem, all constraints are represented as equations. This is because the standard form requires the objective function and constraints to be in the form of equations to ensure consistency and compatibility within the mathematical model.
The correct statement is option 'C': In the standard form of a linear programming problem, all constraints are in the form of equations.
**Explanation:**
Linear programming is a mathematical optimization technique used to determine the best possible outcome in a given mathematical model, given a set of constraints. The standard form of a linear programming problem involves maximizing or minimizing a linear objective function, subject to a set of linear constraints.
In the standard form, the objective function and all constraints must be in the form of equations rather than inequalities. This is because the objective function represents the quantity to be maximized or minimized, and the constraints represent the limitations or restrictions on the variables.
**Reason for Incorrect Options:**
a) Option 'A': Of less than or equal to type
This option is incorrect because linear programming problems may involve constraints of both less than or equal to and greater than or equal to type. However, in the standard form, all constraints are represented as equations.
b) Option 'B': Of greater or equal to type
This option is also incorrect for the same reason as option 'A'. Linear programming problems can have constraints of both types, but in the standard form, they are all represented as equations.
d) Option 'D': Some constraints are of less than equal to type and some are of greater than equal to type
This option is incorrect because, as mentioned earlier, in the standard form, all constraints are represented as equations and not as inequalities of any type.
**Conclusion:**
In the standard form of a linear programming problem, all constraints are represented as equations. This is because the standard form requires the objective function and constraints to be in the form of equations to ensure consistency and compatibility within the mathematical model.
While solving a LP problem, infeasibility may be removed by- a)adding another constraint
- b)adding another variable
- c)removing a constraint
- d)removing a variable
Correct answer is option 'C'. Can you explain this answer?
While solving a LP problem, infeasibility may be removed by
a)
adding another constraint
b)
adding another variable
c)
removing a constraint
d)
removing a variable
|
|
Hrishikesh Chakraborty answered |
Removing Infeasibility in LP Problem
In linear programming (LP) problems, infeasibility means that there is no feasible solution that satisfies all the constraints. Infeasibility can occur due to various reasons such as conflicting constraints, inconsistent data, or incorrect formulation of the problem. In such cases, the LP problem cannot be solved using standard optimization techniques.
To remove infeasibility, one of the following approaches can be taken:
1. Removing a Constraint:
Removing a constraint can make the problem feasible by relaxing the system of constraints. This approach is usually taken when the infeasibility is caused by a single constraint that is too restrictive. By removing this constraint, the feasible region is expanded, and a solution may become feasible. However, this approach should be taken with caution as removing a constraint may change the nature of the problem and the optimal solution.
2. Adding a Variable:
Adding a variable can also make the problem feasible by introducing more degrees of freedom into the system. This approach is usually taken when the infeasibility is caused by the lack of variables to satisfy all the constraints. By adding a variable, the feasible region is expanded, and a solution may become feasible. However, this approach should be taken with caution as adding a variable may increase the complexity of the problem and the computation time.
3. Adding a Constraint:
Adding a constraint can make the problem feasible by restricting the feasible region. This approach is usually taken when the infeasibility is caused by the lack of constraints to satisfy all the variables. By adding a constraint, the feasible region is reduced, and a solution may become feasible. However, this approach should be taken with caution as adding a constraint may make the problem more restrictive and reduce the feasible region further.
Conclusion:
In conclusion, to remove infeasibility in LP problems, one can remove a constraint, add a variable, or add a constraint. However, each approach should be taken with caution as it may change the nature of the problem and the optimal solution.
In linear programming (LP) problems, infeasibility means that there is no feasible solution that satisfies all the constraints. Infeasibility can occur due to various reasons such as conflicting constraints, inconsistent data, or incorrect formulation of the problem. In such cases, the LP problem cannot be solved using standard optimization techniques.
To remove infeasibility, one of the following approaches can be taken:
1. Removing a Constraint:
Removing a constraint can make the problem feasible by relaxing the system of constraints. This approach is usually taken when the infeasibility is caused by a single constraint that is too restrictive. By removing this constraint, the feasible region is expanded, and a solution may become feasible. However, this approach should be taken with caution as removing a constraint may change the nature of the problem and the optimal solution.
2. Adding a Variable:
Adding a variable can also make the problem feasible by introducing more degrees of freedom into the system. This approach is usually taken when the infeasibility is caused by the lack of variables to satisfy all the constraints. By adding a variable, the feasible region is expanded, and a solution may become feasible. However, this approach should be taken with caution as adding a variable may increase the complexity of the problem and the computation time.
3. Adding a Constraint:
Adding a constraint can make the problem feasible by restricting the feasible region. This approach is usually taken when the infeasibility is caused by the lack of constraints to satisfy all the variables. By adding a constraint, the feasible region is reduced, and a solution may become feasible. However, this approach should be taken with caution as adding a constraint may make the problem more restrictive and reduce the feasible region further.
Conclusion:
In conclusion, to remove infeasibility in LP problems, one can remove a constraint, add a variable, or add a constraint. However, each approach should be taken with caution as it may change the nature of the problem and the optimal solution.
Chapter doubts & questions for Linear Programming - 6 Months Preparation for GATE Mechanical 2025 is part of Mechanical Engineering exam preparation. The chapters have been prepared according to the Mechanical Engineering exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Mechanical Engineering 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Linear Programming - 6 Months Preparation for GATE Mechanical in English & Hindi are available as part of Mechanical Engineering exam.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
6 Months Preparation for GATE Mechanical
499 videos|1037 docs|710 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup









